Перемещение при осевом растяжении сжатии

При центральном растяжении и сжатии прямого стержня поперечные сечения, оставаясь плоскими, получают осевые перемещения и (см. рис. 3.7). Они считаются положительными, если их направление совпадает с положительным направлением оси Ох.
Рассмотрим осевые перемещения двух произвольных сечений, отстоящих на расстоянии Ах друг от друга (рис. 3.11). После приложения нагрузки эти сечения получают перемещения соответственно ии и + А и. Длина отрезка Ах после деформации составляет Ах1 = Ах + (и + А и) — и = Ах + А и, а величина удлинения равна Ах, — Ах = Аи.
Рис. З.п
Относительная продольная деформация волокон стержня в сечении х представляет собой предел отношения удлинения А и к первоначальной длине Ах при стремлении последней к нулю:
Проинтегрировав это соотношение в пределах от 0 до х, получим формулу для определения осевого перемещения произвольного сечения:
Обозначив в начальном сечении х = 0 и(0) = и0, получим, что постоянная интегрирования С равна и0. В результате имеем
Учитывая, что на основании (3.6) и (3.5) линейная деформация равна
получим следующую формулу:
Величина ЕЕ называется жесткостью стержня при растяжении и сжатии.
Формула (3.11) позволяет установить характер изменения и(х). Для частного случая, когда жесткость EF и продольная сила N являются постоянными величинами, осевые перемещения изменяются по линейному закону:
На участке, где EF = const, а N является линейной функцией, осевые перемещения изменяются по закону квадратной параболы.
Если начальное сечение х = 0 закреплено, то и0 = 0. Из соотношения (3.10) следует, что в сечении, где е равно нулю (N = 0), и(х) может иметь экстремум.
Удлинение или укорочение стержня длиной / (см. рис. 3.7) равно разности осевых перемещений его концов х = 0 и х = /: А/ = и([) — и(). Согласно формуле (3.11) получим
Для частного случая ЕЕ = const и N = const получим
Для стержня с постоянной жесткостью ЕЕ и линейным законом изменения продольной силы N при определении Д/ удобно использовать геометрический смысл определенного интеграла и привести формулу (3.12) к следующему виду:
где Qn — площадь эпюры N на участке от 0 до /.
Пример 3.2. Для стержня ступенчато-постоянного сечения (рис. 3.12, а) построим эпюры N, о и и. В расчетах примем Е= 1 • 105 МПа.
Рис. 3.12
В данном примере вычисление значений N но производим в характерных сечениях, начиная со свободного конца. При этом мысленно отбрасывается часть стержня, содержащая закрепленное сечение.
Участок 0,8
Сечение х = 2 м, N = 0, о = 0.
Сечение х = 0,8 м, N = 20 • 1,2 = 24 кН (растяжение),
о = = 1,2 кН/см2 = -12 МПа.
Участок 0
Сечение х = 0,8 м, N= 24 — 40 = —16 кН (сжатие), о = —у = -2 кН/см2 = -20 МПа.
Сечение x =0, N — — 16 кН, о = —20 МПа.
Опорная реакция в месте закрепления равна R = 16 кН. Ее направление показано на рис. 3.12, а.
В соответствии с соотношением (3.1) продольная сила и нормальные напряжения в пределах первого участка являются постоянными по величине, а в пределах второго участка изменяются по линейному закону. Эпюры N и с приведены на рис. 3.12, б, в.
Определим величины удлинений (укорочений) участков стержня:
Величина А/ всего стержня равна
В целом стержень укорачивается. Определим величины осевых перемещений характерных сечений:
Все сечения перемещаются в отрицательном направлении оси Ох. В пределах первого участка и(х) изменяется по линейному закону, а в пределах второго участка — по закону квадратной параболы. В сечении вблизи свободного конца касательная к эпюре и параллельна оси стержня, поскольку в этом сечении N= 0. Эпюра и приведена на рис. 3.12, г.
Пример 3.3. Для стержневой системы, состоящей из жесткой балки АВ, поддерживаемой тремя стальными стержнями указанного сечения (рис. 3.13), определим усилия и напряжения в стержнях и величины их удлинений. В расчетах примем Е= 2,1 • 105 МПа.
Для определения усилий Nx, N2 и N3 в стержнях системы используем три уравнения равновесия:
Рис. 3.13
Все три стержня испытывают растяжение. Определим напряжения в стержнях и величины их удлинений.
Стержни CD и DE (_||_63х63х4)
где /j = /2 = V22 + 22 = 2,83 м и /3 = 2 м — длины стержней.
Источник
Растяжение (сжатие) – это такой вид нагружения стержня, при котором в его поперечном сечении возникает внутренняя продольная сила Ν, действующая вдоль центральной оси z.
Продольная сила Ν – это равнодействующая всех внутренних нормальных сил в сечении. Для вычисления продольной силы применяется метод сечений.

Продольная сила Ν численно равна алгебраической сумме проекций всех сил, действующих по одну сторону от рассматриваемого сечения, на продольную ось бруса.
Правило знаков для продольной силы Ν: при растяжении продольная сила положительна, при сжатии – отрицательна.

График изменения продольных сил по длине стержня называется эпюрой. Эпюра N строится методом сечений на характерных участках бруса. Строится эпюра для использования ее при расчете бруса на прочность. Она дает возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.
При растяжении (сжатии) возникают только нормальные напряжения. Согласно гипотезе Я. Бернулли (или гипотеза плоских сечений) в поперечных сечениях, удаленных от места приложения нагрузок, нормальные напряжения распределяются по сечению практически равномерно, а сами сечения, перпендикулярные к оси стержня z, остаются плоскими в процессе нагружения.
Нормальные напряжения в сечении при растяжении (сжатии) вычисляются по формуле
где А – площадь поперечного сечения.
Правило знаков для σ совпадает с правилом знаков для N.
В наклонном сечении, нормаль к которому составляет угол α с осью стержня z,
При растяжении в продольном направлении стержень удлиняется, а его поперечные размеры уменьшаются, при сжатии, напротив, в продольном направлении стержень укорачивается, а его поперечные размеры увеличиваются; Δℓ — абсолютное удлинение или укорочение участка стержня длиной ℓ, Δb – абсолютная поперечная деформация.
Относительное удлинение или укорочение участка стержня длиной ℓ, называемое линейной деформацией, определяется следующим образом
ε=Δℓ/ℓ.
Экспериментально установлено, что в определенной области нагрузок при упругом поведении материала между нормальными напряжениями и линейными деформациями существует линейная зависимость (закон Гука для напряжений)
σ=εЕ,
где Е – модуль продольной упругости или модуль Юнга, это физическая const. Для каждого из материалов величина модуля упругости имеет свое значение:
сталь, Е = 2.105 МПа,
медь, Е = 1.105 МПа,
алюминий, Е = 0,7.105 МПа.
Значение модуля упругости устанавливается экспериментально.
Согласно закону Гука (данную запись называют законом Гука для деформаций)
Δℓ=Νℓ/ЕА
Произведение ЕА – называется жесткостью стержня при растяжении – сжатии.
Перемещение произвольного сечения ступенчатого стержня
w=∑Δℓi
Относительная поперечная деформация:
ε′=Δb/b
где b – поперечный размер стержня.
Эксперименты также показывают, что в упругой стадии деформирования между продольной и поперечной деформациями существует взаимосвязь
μ =│ε′⁄ε│ — const,
где μ — коэффициент Пуассона, берется по модулю ,поскольку у продольной и поперечной деформации разные знаки (при растяжении продольные волокна увеличиваются, а поперечные уменьшаются в размере).
Для твердых материалов имеет значения коэффициент Пуассона
0≤μ ≤0,5
Изменение температуры стержня вызывает его удлинение (при нагревании) или укорочение (при охлаждении)

где — a- коэффициент линейного температурного расширения; Δtº=(tºк-tºн) — изменение температуры между значениями начальным (tºн) и конечным (tºк).
Статически неопределимыми называют системы, имеющие лишние связи – внешние или внутренние.
Для определения внутренних усилий в таких системах недостаточно рассматривать только уравнения равновесия.
В этом случае требуются дополнительные уравнения, число которых равно количеству лишних связей. Дополнительные уравнения составляются на основе анализа картины деформирования системы и использования законов деформирования ее элементов.
Алгоритм решения подобных задач включает следующее:
1) Статическая часть. Составляются уравнения равновесия с включением неизвестных усилий, действующих по направлению лишних связей.
2) Геометрическая часть. Составляются уравнения, описывающие взаимосвязь перемещений характерных точек, удлинений и укорочений отдельных стержней между собой.
3) Физическая связь. Записываются законы деформирования отдельных стержней системы.
Порядок расчета статически неопределимых брусьев
- Задаться направлениями возможных опорных реакций и составить уравнение статики для всей системы в целом.
- Определить степень статической неопределимости и использовать метод сечений с целью выразить неизвестные усилия через неизвестные опорные реакции. При этом неизвестные продольные силы (N) следует предполагать положительными и поэтому направлять «от сечения».
- Сформулировать условие совместности деформаций участков бруса.
- В процессе превращения условия совместности в уравнение совместности деформаций различий в характере деформаций участков не учитывать.
Порядок расчета статически неопределимых шарнирно-стержневых систем
- Задаться направлениями опорных реакций, но уравнений равновесия для всей системы не составлять, а сразу использовать метод сечений и составить уравнения статики для выделенной части системы.
- Определить степень статической неопределимости как разницу между количеством всех неизвестных, оказавшихся в уравнениях статики, и числом самих этих уравнений.
- Рассмотреть (изобразить) любую возможную картину деформаций системы и из ее анализа сформулировать условия совместности деформаций стержней системы (столько, какова степень статической неопределимости).
- В процессе преобразования условий совместности в уравнения совместности деформаций обязательно учитывать различие в характере деформаций стержней (т.е. вводить удлинение со знаком «плюс», а укорочение со знаком «минус») в соответствии с той картиной деформации, которую мы рассматриваем.
Источник
Напряжения и деформации. Коэффициент Пуассона. Закон Гука
Осевое растяжение (рис. 2.1, а) и сжатие (рис. 2.1, б) возникают под действием сил, направленных вдоль оси бруса (стержня). При растяжении (сжатии) в поперечном сечении бруса возникает только одно внутреннее усилие — продольная сила N. На растяжение (сжатие) работают канаты, стержни ферм и т.п. Растяжение (сжатие) могут вызвать сосредоточенные силы и продольная распределенная нагрузка (рис. 2.2). Здесь q — интенсивность продольной распределенной нагрузки, сила, приходящаяся на единицу длины, Н/м, кН/м.
Рис. 2.1. Осевое растяжение (а) и сжатие (б)
Рис. 2.2. Элемент, работающий на растяжение
Изобразим стержень, который подвергается центральному растяжению (рис. 2.3). Для определения внутренних сил применим метод сечений. В произвольном сечении стержня покажем внутренние усилия, которые при данном виде нагружения будут совпадать с направлением нормальных напряжений.
Рис. 2.3. Дефрмации при осевом растяжении (а) и равнодействующая внутренних сил (б): / — исходное состояние; 2 — деформационное состояние
Равнодействующая внутренних усилий будет состоять только из продольной составляющей:
Она будет приложена в центре тяжести сечения стержня, который совпадает с продольной осью.
При расчетах по методу сечений будем всегда продольную силу направлять наружу. Если N > 0, то она направлена верно, а если получается, что jV
Составим уравнение равновесия отсеченной части:
Из гипотезы плоских сечений, высказанной голландским ученым Д. Бернулли, следует, что в пределах действия закона Гука плоские поперечные сечения стержня смещаются при растяжении параллельно начальным положениям, оставаясь плоскими (рис. 2.3, б). Это возможно лишь в случае, если нормальные напряжения во всех точках сечения одинаковы, т.е. О = const. Отсюда следует:
Под действием осевых растягивающих сил стержень постоянного сечения площадью А удлиняется на величину
где /j и /0 — длины стержня в деформированном и начальном состояниях;
А/ — абсолютное или полное удлинение.
Относительное удлинение
При растяжении и сжатии возникает также и поперечная деформация стержня
где и а — ширина стержня в деформированном и первоначальном состояниях; А а — абсолютная поперечная деформация.
Относительная поперечная деформация
Знак (-) показывает, что при растяжении поперечные размеры стержня уменьшаются.
Коэффициент Пуассона. Отношение поперечной деформации к продольной при растяжении (сжатии), взятое по абсолютной величине, называют коэффициентом Пуассона:
Значение V для всех материалов находится в пределах 0
Закон Гука. Для подавляющего большинства конструкционных материалов с достаточной для практики точностью можно считать, что в известных пределах нагружения между продольной деформацией и соответствующим (действующим в ее направлении) нормальным напряжением существует пропорциональная (линейная) зависимость. Эта зависимость носит название закона Гука и записывается в виде
где Е — коэффициент пропорциональности, именуемый модулем упругости первого рода (модуль Юнга).
По физическому смыслу модуль упругости — напряжение, которое вызывает деформацию ? = 1 (удлинение стержня, равное первоначальной длине).
Для статей по данным экспериментов Е = (2…2,2)105 МПа для ста-
N А/
леи. Учитывая, что О = —, ? = —, закон Гука для растянутого стержня можно записать
где X] =— — коэффициент податливости стержня, показывающий уд-
is • А
линение (укорочение) стержня, вызываемое растягивающей силой F= 1 Н.
Произведение ЕА называют жесткостью сечения стержня при растяжении (сжатии). Для стержней переменного (ступенчатого) сечения удлинения определяют по участкам (ступеням) и результаты суммируют алгебраически:
где i — номер участка (i = 1, 2,…,«).
При расчете упругих перемещений стержня от нескольких сил часто применяют принцип независимости действия сил: перемещение стержня от действия группы сил может быть получено как сумма перемещений от действия каждой силы в отдельности.
Пример 2.1. Определить полное удлинение стержня (рис. 2.4).
Решение
Рис. 2.4. Определение внутренних сил и построение их эпюры
Определим с помощью метода сечений значения продольной силы на каждом участке. Для этого сделаем три сечения. Рассмотрим равновесие отсеченных частей:
Изобразим графически распределение продольных сил по длине стержня. График изменения продольных сил по длине стержня называется эпюрой. Каждая ордината эпюры равна значению N в данном сечении. Эпюру строят на линии, проведенной параллельно оси стержня. Подставив найденные значения N, N2, N3 в формулу, определим общее удлинение стержня
Пример 2.2. Определить величину напряжения О. возникающего в поперечном сечении, абсолютное удлинение Д/ и относительное укорочение ? стального стержня диаметром d = 40 мм, длиной / = 1,5 м, растягиваемого силой F = 100 кН, если Е = 2,1 • 105 Н/мм2 (рис. 2.5).
Рис. 2.5. К примеру 2.2
Решение
Площадь сечения
Напряжение
Абсолютное удлинение
Относительное удлинение
Пример 2.3. Стальная штанга длиной / = 8 м и площадью сечения А = 8 см2 под действием растягивающей нагрузки получила абсолютное удлинение А/ = 5,7 мм. Определить величину нагрузки F и напряжения G, если известно, что модуль упругости материала тяги Е = 2,МО5 МПа (рис. 2.6).
Решение
Относительное удлинение
Величина напряжения
Величина нагрузки
Рис. 2.6. К примеру 2.3
Источник
Если нормальная
сила и поперечное сечение меняются по
длине ступенчато, то стержень надо
разбить на участки, так чтобы в пределах
каждого участка
![]()
и
![]()
были постоянны, определить удлинение
каждого из участков и тогда полное
удлинение стержня будет равняться
алгебраической сумме, (знак определяется
знаком
![]() )
)
удлинений участков.
Е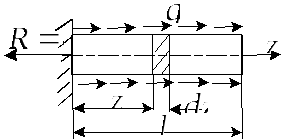 сли
сли
же напряженное состояние в стержне
неоднородно, то выделив малый элемент
длиной
![]() определим
определим
его удлинение
![]() ,
,
Здесь
![]()
и
![]()
рассматривается как функции z.
Полное удлинение стержня будет равно:
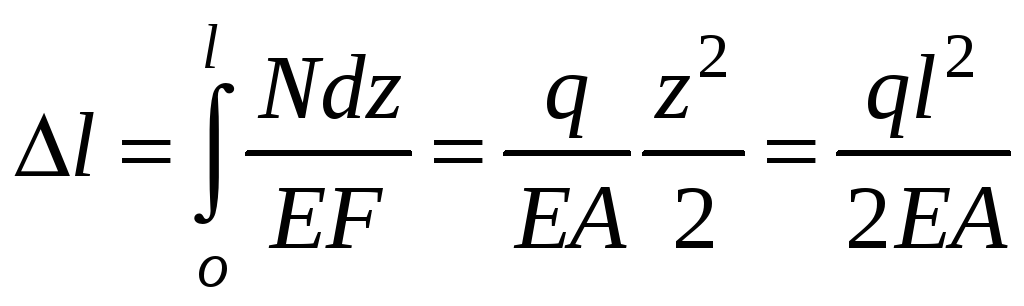
16)
Закон парности касательных напряжений (из напряжений по косым площадкам)
Выясним, каковы
касательные напряжения по площадке
перпендикулярной данной, т.е. задаваемой
углом
![]()
![]() т.е.
т.е.
![]()
Знак
“минус” указывает на то, что касательные
напряжения на взаимно перпендикулярных
площадках направлены либо к ребру между
площадками либо от ребра. Таким образом
имеет место
закон парности касательных напряжений.
Касательные
напряжения по взаимно перпендикулярным
площадкам равны по величине и направлены
как было указано выше.
17)
Расчёты на прочность (проектировочный, проверочный, определение несущей способности)

18)
Напряженное состояние при растяжении и сжатии (напряжения по косым площадкам)
Во вводной лекции
мы уже упоминали о напряженном состоянии
в точке и в частности, говорили, что
знать напряженное состояние в точке –
это уметь вычислить напряжения по любой
площадке, проходящей через данную точку.
Теперь уже мы рассмотрим этот вопрос в
случае, когда исследуемая точка
принадлежит растянутому или сжатому
стержню.
П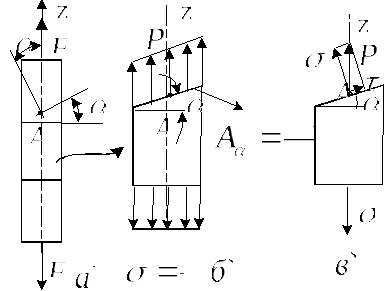 усть
усть
стержень растянут силой F
и в поперечных сечениях стержня, как мы
знаем, возникают нормальные напряжения
равные
![]() ,
,
где А — площадь поперечного сечения.
Проведем через
исследуемую точку А произвольное
сечение, положение которого задается
углом
![]()
между осью стержня и внешней нормалью
к сечению. Кроме того, проведем еще
поперечное сечение. Выделим с помощью
указанных сечений элемент и рассмотрим
равновесие данного элемента.
По наклонной
площадке действует полное напряжение
![]() .
.
проектируя силы, действующие на элемент
на ось стержня, получаем
![]()
![]()
Разлагая
![]()
на нормальное
![]()
и касательное напряжение, получаем
![]()
![]()
Переходя к функциям
угла
![]()
имеем
![]()
Уравнения (5) дают
возможность вычислить напряжения по
любым площадкам, проходящим через данную
точку, т.е. определяют напряженное
состояние при растяжении и сжатии.
Очевидно, что касательные напряжения
обращаются в нуль по двум площадкам
![]()
(поперечное сечение) и
![]()
(продольное сечение). Площадки, по которым
касательные напряжения равны нулю,
называются главными площадками, а
нормальные напряжения, действующие по
ним, главными напряжениями.
Очевидно, что одно
из главных напряжений, действующее в
поперечном сечении —
![]()
является максимальным по модулю, что
обосновывает использование формулы
(1), как основной расчетной формулы при
растяжении, сжатии, а другое главное
напряжение, действующее в продольных
площадках рано нулю. Таким образом,
продольные площадки свободны от
напряжений.
Из второго уравнения
(5) видно, что максимальные касательные
напряжения возникают по площадкам,
наклоненным к оси на угол
![]() ,
,
и равняются по величине
![]()
Максимальные
касательные напряжения являются причиной
разрушения образцов из хрупких материалов,
испытываемых на сжатие.
19)_А
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
