Относительное продольное удлинение на растяжение

ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ
ИНСТИТУТ
СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
им. В.А. КУЧЕРЕНКО ГОССТРОЯ СССР
РЕКОМЕНДАЦИИ
ПО МЕТОДИКЕ ОПРЕДЕЛЕНИЯ
ОТНОСИТЕЛЬНОГО РАВНОМЕРНОГО
УДЛИНЕНИЯ СТРОИТЕЛЬНЫХ
СТАЛЕЙ ПРИ ИСПЫТАНИИ
НА РАСТЯЖЕНИЕ
Утверждены директором ЦНИИСК
им. В.А.
Кучеренко
27 апреля 1979 г.
МОСКВА — 1980
Рекомендации распространяются
на стальной
прокат для строительных металлических
конструкций и устанавливают методы определения относительного равномерного
удлинения как характеристики, нормируемой
техническими условиями, так и необходимой при
проведении научно-исследовательских работ.
Рекомендации предназначены
для инженерно-технических работников заводских
лабораторий (заводов строительных металлоконструкций)
и научно-исследовательских организаций.
Рис. 2.
СОДЕРЖАНИЕ
При работе стали в
конструкциях характеристика относительного равномерного удлинения играет важную роль для
оценки способности металла пластически деформироваться. Эта характеристика
имеет большее значение, чем нормируемое в настоящее время полное относительное
удлинение согласно ГОСТ 1497-73. До настоящего времени для определения равномерного
относительного удлинения в основном использовалась методика, описанная в
стандарте на арматурные стали, где не предусмотрены плоские образцы.
Настоящее руководство
распространяется на стальной толстолистовой, широкополосный универсальный и
фасонный (уголок, швеллер, балка) прокат толщиной от 4 до 40 мм, независимо от
его прочностных свойств, предназначенный для изготовления
строительных металлических конструкций, и
устанавливает методы определения относительного равномерного удлинения при
статических испытаниях
на растяжение при нормальных температурах ![]() .
.
Применение методов
определения относительного равномерного удлинения предусматривается в
стандартах и технических условиях на соответствующие виды проката,
предназначенного для строительных металлических конструкций.
Термины и определения,
принятые в настоящих рекомендациях, согласованы с ГОСТ 1497-73 «Металлы. Методы испытания на растяжение».
Относительное равномерное
удлинение определяется одновременно с относительным удлинением после разрыва.
Настоящие рекомендации
разработаны Отделением прочности и новых форм металлических конструкций и
Отделением испытаний конструкций ЦНИИСК им. Кучеренко Госстроя СССР (составили кандидаты
технических наук Потапов В.Н. и Жулев Ю.К.) на
основании материалов исследований, выполненных
в период 1976-78 гг.
Дирекция ЦНИИСК
им. Кучеренко
1.1. При испытании на
растяжение по определению относительного равномерного удлинения принимаются
следующие обозначения и определения:
l — рабочая длина в мм — часть образца с постоянной площадью поперечного сечения между его
головкой или участком для захвата;
l0 — начальная расчетная длина образца в мм, на которой
определяется удлинение после разрыва;
lпр — начальная расчетная длина участка образца в мм, на которой
определяется равномерное удлинение;
lкр — конечная расчетная длина участка образца в мм, не
включающая место разрыва;
lт — установочная база измерителя деформаций в мм;
d0 — начальный диаметр рабочей части цилиндрического образца до
разрыва в мм;
F0 — начальная площадь поперечного сечения рабочей части образца в мм2;
Fкр — конечная площадь поперечного сечения рабочей части образца после
разрыва, определяемая в расчетной части равномерного
относительного удлинения в мм2.
1.2. Характеристики
механических свойств, получаемых при испытании на растяжение, имеют следующие
обозначения и определения:
δр — относительное равномерное удлинение после разрыва в % — отношение приращения расчетной длины образца (lкр — lнр) на участке, не
включающем место разрыва, к соответствующей первоначальной длине lнр;
ψp — относительное равномерное сужение в % — отношение изменения
площади поперечного сечения образца (F0 — Fкр) после разрыва на участке, не включающем место разрыва, к начальной площади поперечного сечения;
Pвр — максимальная осевая растягивающая нагрузка в кГс, действующая
на образец до образования шейки.
2.1. Для определения
относительного равномерного удлинения при испытании на растяжение применяют
пропорциональные плоские образцы типов I и II с начальной расчетной длиной ![]() а также пропорциональные цилиндрические образцы типов I — VII
а также пропорциональные цилиндрические образцы типов I — VII
с l0 = 10d0 по ГОСТ 1497-73.
2.2. Рабочая длина плоского
образца должна составлять
![]()
2.3. При испытании
толстолистового широкополосного и уголкового проката применяют, как правило, плоские образцы. При
испытании швеллерного и двутаврового проката применяют, в основном,
цилиндрические образцы; допускается применение плоских образцов с одной прокатной и другой
обработанной поверхностями.
Плоские образцы должны сохранять
поверхностные слои проката. При толщине проката свыше 25 мм:
— испытания проводят на
плоских образцах толщиной 25 мм с одной прокатной поверхностью;
— допускается применять
плоские образцы
с обеими прокатными поверхностями, принимая при этом ширину образца не менее 50
мм и расчетную длину ![]() .
.
2.4. Измерение начальной и
конечной расчетных длин, размеров поперечного
сечения образца производят с точностью до 0,1 мм.
2.5. На рабочей части образца
рекомендуется наносить разметку — неглубокие керны, риски или иные метки через каждые 5 или
10 мм.
3.1. Для испытаний применяют
разрывные и универсальные машины всех систем, если они соответствуют
требованиям ГОСТ 1497-73, ГОСТ 7855-74
и требованиям
стандартов на стали для строительных металлических конструкций.
3.2. При проведении испытаний
должны соблюдаться следующие основные условия:
а) надежное центрирование
образца в захватах испытательной машины;
б) плавность нагружения;
в) скорость перемещения активного захвата при
испытании до предела текучести долина быть не
более 0,01, за пределом текучести не более 0,2 длины расчетной части образца,
выраженной в мм/мин.
4.1. При текущих испытаниях
определение относительного равномерного
удлинения может производиться по одному из
следующих методов:
Первый метод
Относительное равномерное
удлинение δр определяют вне участка разрыва (предпочтительней на
большей части разрушенного образца) на начальной расчетной длине, равной 50 мм.
При этом расстояние от места разрыва до
ближайшей точки (риски) начальной расчетной
длины lпр должно быть не менее 3b0*) (с округлением до ближайшей удаленной
разметочной риски от места разрыва образца где
b0 — начальная ширина образца (рис. 1).
______________
*)
В случае цилиндрических образцов вместо b0 следует d0.
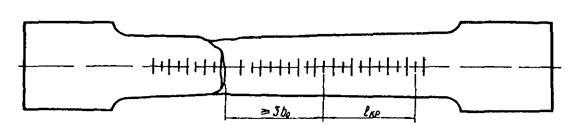
Рис. 1
Относительное равномерное
удлинение δр в процентах вычисляют по формуле
![]()
Второй метод
Относительное равномерное
удлинение δр в % вычисляют по следующей формуле
![]()
где ψр — относительное равномерное сужение в %, вычисленное по формуле
![]()
Измерение площади Fкр производится на расстоянии от места
разрыва не менее 4b0.
Третий метод*)
______________
*) Этот метод
допускает использование образцов с пятикратной расчетной длиной.
Относительное равномерное
удлинение δр определяют графически по диаграмме растяжения (рис. 2), записываемой соответствующим измерителем деформаций, установленным непосредственно на
образце.
Масштаб по оси деформаций
должен быть не менее 50:1.
Примечание. Определение δр производится на
участке диаграммы растяжения, заканчивающемся точкой В, которая соответствует
началу достижения максимальной нагрузки Рвр.
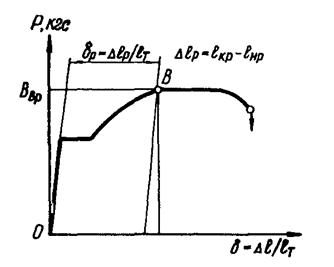
Рис. 2
4.2. Относительное
равномерное удлинение вычисляют с округлением до 0,5 %. При этом доли до 0,25 %
отбрасывают, а доли в 0,25 % и более принимают за 0,5 % (см. приложение).
4.3. Испытание считается
недействительным:
— при разрыве
образца по кернам (рискам), если при этом какая-либо
характеристика механических свойств по своей величине не отвечает установленным требованиям;
— при разрыве
образца в захватах испытательной машины или за пределами расчетной длины;
— при обнаружении ошибок в
проведении испытаний или записи результатов
испытаний.
В указанных случаях испытание
на растяжение должно быть повторено на отобранных от той же партии или плавки
новых образцах.
По первому методу (рис. 1)
Начальная расчетная длина lнр = 50
мм;
Конечная расчетная длина lкр = 58,4 мм,
![]()
По второму методу
Начальная площадь поперечного сечения
(10×30 мм) образца F0 = 300 мм2.
Конечная площадь поперечного
сечения образца (замеренная на расстоянии 4b0 от места разрыва) Fкр = 258 мм2
|
|
Источник
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Иметь представление о продольных и поперечных деформациях и их связи.
Знать закон Гука, зависимости и формулы для расчета напряжений и перемещений.
Уметь проводить расчеты на прочность и жесткость статически определимых брусьев при растяжении и сжатии.
Деформации при растяжении и сжатии
Рассмотрим деформацию бруса под действием продольной силы F (рис. 21.1).
В сопротивлении материалов принято рассчитывать деформации в относительных единицах:
Между продольной и поперечной деформациями существует зависимость
где μ— коэффициент поперечной деформации, или коэффициент Пуассона, —характеристика пластичности материала.
Закон Гука
В пределах упругих деформаций деформации прямо пропорциональны нагрузке:
где F — действующая нагрузка; к — коэффициент. В современной форме:
Получим зависимость
где Е — модуль упругости, характеризует жесткость материала.
В пределах упругости нормальные напряжения пропорциональны относительному удлинению.
Значение Е для сталей в пределах (2 – 2,1) • 105МПа. При прочих равных условиях, чем жестче материал, тем меньше он деформируется:
Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии
Используем известные формулы.
Относительное удлинение
В результате получим зависимость между нагрузкой, размерами бруса и возникающей деформацией:
где
Δl — абсолютное удлинение, мм;
σ — нормальное напряжение, МПа;
l — начальная длина, мм;
Е — модуль упругости материала, МПа;
N — продольная сила, Н;
А — площадь поперечного сечения, мм2;
Произведение АЕ называют жесткостью сечения.
Выводы
1. Абсолютное удлинение бруса прямо пропорционально величине продольной силы в сечении, длине бруса и обратно пропорционально площади поперечного сечения и модулю упругости.
2. Связь между продольной и поперечной деформациями зависит от свойств материала, связь определяется коэффициентом Пуассона, называемом коэффициентом поперечной деформации.
Коэффициент Пуассона: у стали μ от 0,25 до 0,3; у пробки μ = 0; у резины μ = 0,5.
3. Поперечные деформации меньше продольных и редко влияют на работоспособность детали; при необходимости поперечная деформация рассчитывается через продольную.
где Δа — поперечное сужение, мм;
ао — начальный поперечный размер, мм.
4. Закон Гука выполняется в зоне упругих деформаций, которая определяется при испытаниях на растяжение по диаграмме растяжения (рис. 21.2).
При работе пластические деформации не должны возникать, упругие деформации малы по сравнению с геометрическими размерами тела. Основные расчеты в сопротивлении материалов проводятся в зоне упругих деформаций, где действует закон Гука.
На диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.
5. Определение деформации бруса под нагрузкой и сравнение ее с допускаемой (не нарушающей работоспособности бруса) называют расчетом на жесткость.
Примеры решения задач
Пример 1. Дана схема нагружения и размеры бруса до деформации (рис. 21.3). Брус защемлен, определить перемещение свободного конца.
Решение
1. Брус ступенчатый, поэтому следует построить эпюры продольных сил и нормальных напряжений.
Делим брус на участки нагружения, определяем продольные силы, строим эпюру продольных сил.
2. Определяем величины нормальных напряжений по сечениям с учетом изменений площади поперечного сечения.
Строим эпюру нормальных напряжений.
3. На каждом участке определяем абсолютное удлинение. Результаты алгебраически суммируем.
Примечание. Балка защемлена, в заделке возникает неизвестная реакция в опоре, поэтому расчет начинаем со свободного конца (справа).
1. Два участка нагружения:
участок 1:
растянут;
участок 2:
2.
Три участка по напряжениям:
Пример 2. Для заданного ступенчатого бруса (рис. 2.9, а) построить эпюры продольных сил и нормальных напряжений по его длине, а также определить перемещения свободного конца и сечения С, где приложена сила Р2. Модуль продольной упругости материала Е = 2,1 • 105 Н/’мм3.
Решение
1. Заданный брус имеет пять участков /, //, III, IV, V (рис. 2.9, а). Эпюра продольных сил показана на рис. 2.9, б.
2. Вычислим напряжения в поперечных сечениях каждого участка:
для первого
для второго
для третьего
для четвертого
для пятого
Эпюра нормальных напряжений построена на рис. 2.9, в.
3. Перейдем к определению перемещений поперечных сечений. Перемещение свободного конца бруса определяется как алгебраическая сумма удлинений (укорочений) всех его участков:
Подставляя числовые значения, получаем
4. Перемещение сечения С, в котором приложена сила Р2, определяется как алгебраическая сумма удлинений (укорочений) участков ///, IV, V:
Подставляя значения из предыдущего расчета, получаем
Таким образом, свободный правый конец бруса перемещается вправо, а сечение, где приложена сила Р2, — влево.
5. Вычисленные выше значения перемещений можно получить и другим путем, пользуясь принципом независимости действия сил, т. е. определяя перемещения от действия каждой из сил Р1; Р2; Р3 в отдельности и суммируя результаты. Рекомендуем учащемуся проделать это самостоятельно.
Пример 3. Определить, какое напряжение возникает в стальном стержне длиной l = 200 мм, если после приложения к нему растягивающих сил его длина стала l1 = 200,2 мм. Е = 2,1*106 Н/мм2.
Решение
Абсолютное удлинение стержня
Продольная деформация стержня
Согласно закону Гука
Пример 4. Стенной кронштейн (рис. 2.10, а) состоит из стальной тяги АВ и деревянного подкоса ВС. Площадь поперечного сечения тяги F1 = 1 см2, площадь сечения подкоса F2 = 25 см2. Определить горизонтальное и вертикальное перемещения точки В, если в ней подвешен груз Q = 20 кН. Модули продольной упругости стали Eст = 2,1*105 Н/мм2, дерева Ед = 1,0*104 Н/мм2.
Решение
1. Для определения продольных усилий в стержнях АВ и ВС вырезаем узел В. Предполагая, что стержни АВ и ВС растянуты, направляем возникающие в них усилия N1 и N2 от узла (рис. 2.10, 6). Составляем уравнения равновесия:
откуда
Усилие N2 получилось со знаком минус. Это указывает на то, что первоначальное предположение о направлении усилия неверно — фактически этот стержень сжат.
2. Вычислим удлинение стальной тяги Δl1и укорочение подкоса Δl2:
где
Тяга АВ удлиняется на Δl1= 2,2 мм; подкос ВС укорачивается на Δl1= 7,4 мм.
3. Для определения перемещения точки В мысленно разъединим стержни в этом шарнире и отметим их новые длины. Новое положение точки В определится, если деформированные стержни АВ1 и В2С свести вместе путем их вращения вокруг точек А и С (рис. 2.10, в). Точки В1 и В2 при этом будут перемещаться по дугам, которые вследствие их малости могут быть заменены отрезками прямых В1В’ и В2В’, соответственно перпендикулярными к АВ1 и СВ2. Пересечение этих перпендикуляров (точка В’) дает новое положение точки (шарнира) В.
4. На рис. 2.10, г диаграмма перемещений точки В изображена в более крупном масштабе.
5. Горизонтальное перемещение точки В
Вертикальное
где составляющие отрезки определяются из рис. 2.10, г;
Подставляя числовые значения, окончательно получаем
При вычислении перемещений в формулы подставляются абсолютные значения удлинений (укорочений) стержней.
Контрольные вопросы и задания
1. Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относительное сужение? (μ = 0,25.)
2. Что характеризует коэффициент поперечной деформации?
3. Сформулируйте закон Гука в современной форме при растяжении и сжатии.
4. Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?
5. Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?
6. Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?
7. Ответьте на вопросы тестового задания.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Источник
