Осевое растяжение сжатие задачи с решением
Пример решения задачи на растяжение и сжатие
.
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) с размерами см; см, см и площадью поперечного сечения нижнего участка см2, а верхнего – см2 нагружен внешними осевыми силами кН и кН. Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Расчетная схема для задачи на растяжение и сжатие
рис 3.2
Решение пример задачи на растяжение и сжатие
Определяем значение опорной реакции , возникающей в заделке
Учитывая, что , направим опорную реакцию вниз. Тогда из уравнения равновесия находим:
кН.
Строим эпюру продольных сил
Разбиваем длину стержня на три участка. Границами участков являются сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений. Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Cечение 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. 3.2, б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила уравновесит внешнюю силу . Поэтому очевидно, что
кН.
Сечение 2 – 2. Внешняя сила растягивает рассматриваемую нами нижнюю часть стержня, а сила ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила , противодействующая сжатию, то есть направленная к сечению. Она равна:
кН.
Сечение 3 – 3. Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю (реактивную) сжимающую силу . Поэтому она направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействует сжатию. Она равна:
кН.
При построении эпюры продольных сил будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию. Оно вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому кН.
Для построения эпюры продольных сил проводим тонкой линией ось, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. 3.2, д, никак не сказывается на характере эпюры .
Строим эпюру нормальных напряжений
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и – продольная сила и площадь k–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
кН/см2,
во втором –
кН/см2,
в третьем –
кН/см2.
Строим по вычисленным значениям эпюру (рис. 3.2, е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
Оцениваем прочность стержня
Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем случае
кН/см2 > кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
Вычисляем удлинение всего стержня
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
,
где E – модуль Юнга, а – длина соответствующего участка стержня.
Тогда
см.
Таким образом, длина стержня уменьшается на мм.
Задача по сопромату на растяжение и сжатие для самостоятельного решения
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) находится под действием внешних осевых сил и (рис. 3.1). Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Схемы для задачи на растяжение и сжатие
Исходные данные к задаче на растяжение и сжатие
Номер схемы | F, см2 | a, м | b, м | c, м | P, кН |
1 | 2,0 | 1,2 | 1,4 | 1,6 | 11 |
2 | 2,2 | 1,4 | 1,6 | 1,4 | 12 |
3 | 2,4 | 1,8 | 1,6 | 1,2 | 13 |
4 | 2,6 | 1,6 | 2,0 | 1,0 | 14 |
5 | 2,8 | 2,0 | 1,8 | 1,2 | 15 |
6 | 3,0 | 2,2 | 1,6 | 1,4 | 16 |
7 | 3,2 | 2,4 | 1,4 | 1,6 | 17 |
8 | 3,4 | 2,6 | 1,2 | 1,8 | 18 |
9 | 3,6 | 2,8 | 1,0 | 1,4 | 19 |
3,8 | 2,4 | 1,6 | 1,2 | 20 |
Источник
1.1 (Вариант 4) Конструкция состоит из двух стержней, соединенных между собой и с основанием шарнирами (рис.1). К шарнирному болту С привязан груз Р. Требуется определить внутренние усилия в стержнях и подобрать их сечение по допускаемым напряжениям на сжатие и растяжение. Величина силы Р, форма сечения и допускаемые напряжения приведены в табл.1. 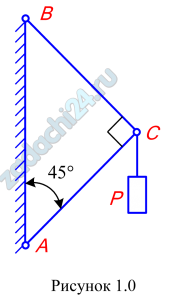
Таблица 1
| Сечение стержней | Величина Р, кН | [σ]С, МПа | [σ]Р, МПа |
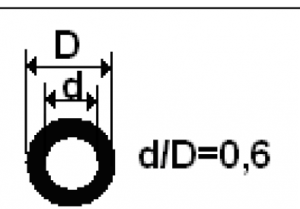 | 10 | 160 | 100 |
Ответ: NBC=7,1 кН, NAC=-7,1 кН, D=15,0 мм, d=9,0 мм.
1.2 (Вариант 29) Двухступенчатый стальной брус, длины ступеней которого указаны на рис.23 (схемы I-X) нагружены силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение (укорочение) бруса, приняв Е=2·105 МПа. Числовые значения сил F1 и F2, а также площадей поперечных сечений ступеней A1 и A2 для своего варианта взять из табл.8.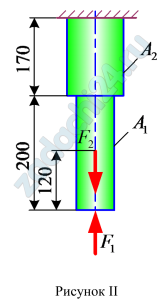
Таблица 8 — Исходные данные
| № задачи и схемы на рис.23 | F1, кН | F2, кН | А1, см2 | А2, см2 |
| 62,II | 4,8 | 10,0 | 0,4 | 0,8 |
Ответ: Δl=0,113·10-3 м.
1.3 (Вариант 2396) Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки F и при найденном значении нагрузки вычислить наибольшее перемещение бруса, а также максимальное удлинение участка a.
Принять А=200 мм², l=200 мм, s=2, остальные данные взять из табл.3.1 и табл.3.2.
Источник
Величина силы, приложенной к стержню, пока неизвестна, она будет найдена позднее из условия прочности. Но составление условия прочности потребует использования формул для напряжений в сечениях, значит, продольных сил, опорных реакций и т. д.
Для определения опорных реакций составим уравнение равновесия:
, . (1)
К нему добавим уравнение деформаций:
Здесь – общее удлинение всего стержня. Для его вычисления отбрасываем правую опору, но её действие заменяем неизвестной опорной реакцией (схема г). Тогда получается, что к стержню приложены две внешние активные силы: F и R2. По принципу независимости действия сил определяем удлинения от каждой из них и результаты суммируем:
Упростим левую часть:
(2)
Уравнения (1), (2) представляют систему уравнений относительно двух неизвестных R1 и R2. Отсюда получим
,
Находим продольные силы в сечениях участков с помощью метода сечений:
(3)
Им соответствуют напряжения в поперечных сечениях:
– растягивающие напряжения, (4)
– сжимающие напряжения, (5)
– сжимающие напряжения. (6)
Грузоподъёмность системы должна быть определена по прочности наиболее напряжённого участка. Между тем, при неизвестном значении силы F определить наибольшее по абсолютному значению напряжение из трёх, вычисляемых формулами (4) – (6), не удаётся. Легко сравниваются только σ2 и σ3. Очевидно, что σ2 = 2σ3. Значит, определение грузоподъёмности придётся производить дважды: по прочности первого участка и прочности второго участка. Окончательное значение грузоподъёмности будет равно меньшему из значений.
Расчёты по прочности первого участка. Условие прочности имеет вид
. (7)
Подставим (4) в (7) и запишем
Отсюда получим грузоподъёмность как наибольшее значение допускаемой силы:
(8)
Расчёты по прочности второго участка. Условие прочности имеет вид
. (9)
Здесь появление знака минус вызвано следующей необходимостью. Напряжение σ2 отрицательное, в то время как допускаемое напряжение [σ] положительное. Их сравнение возможно только при наличии минуса в левой части условия прочности.
Подставляя (5) в (9), имеем
Отсюда
(10)
Окончательно получим значение грузоподъёмности как меньшее из двух результатов: (8) или (10)
[F] = min {[F]1, [F]2} = [F]1 = 93333 Н.
Теперь можно провести вычисления для построения эпюр.
Продольные силы по формулам (3)
По этим значениям строим эпюру продольных сил д).
Напряжения в поперечных сечениях находим по формулам (4)–(6):
Этот результат можно было предсказать. Напряжение в сечениях первого участка должно равняться допускаемому напряжению, так как по условию прочности именно первого участка: σ1 = [σ] была найдена сила [F]. Факт совпадения найденного напряжения с допускаемым подтверждает правильность проведённых вычислений:
По этим значениям строим эпюру нормальных напряжений е).
На схеме а) наметим характерные точки B, C, D, G, для которых будем определять перемещения. Точка B закреплена, поэтому
uB= 0.
Перемещение точки С равно удлинению первого участка стержня, т. е.
Перемещение точки D равно сумме деформаций первого и второго участков:
Перемещение uC уже найдено, поэтому можно вычислить
Перемещение точки G равно сумме
Как и следовало ожидать, перемещение точки G равно величине зазора. Такое совпадение также подтверждает правильность выполненных расчётов. По этим значениям строим эпюру перемещений ж).
Исходные данные
Второе число шифра | l м | Aмм | D мм | sт МПа | nт |
1 | 1,2 | 180 | 0,7 | 240 | 1,5 |
2 | 1,1 | 190 | 0,5 | 280 | 2,0 |
3 | 1,0 | 200 | 0,6 | 300 | 1,5 |
4 | 1,3 | 210 | 0,9 | 320 | 1,6 |
5 | 1,4 | 190 | 0,8 | 340 | 1,7 |
расчётные схемы


Задача 5
Растяжение – сжатие упруго-пластической статически
неопределимой стержневой системы
Шарнирно-стержневая система состоит из тяг, материал которых является идеально упруго-пластическим, и абсолютно жёсткого бруса. Требуется:
1. Вычислить силу F = Fт, при достижении которой в одной из тяг начинаются пластические деформации, и соответствующие ей значения продольных сил в тягах N1Т, N2Т и перемещения dBТ точки B;
2. Вычислить предельную нагрузку F = Fпр и соответствующие ей значения продольных сил в тягах N1пр, N2пр и перемещения dВпр= dВ(Fпр–0).
3. Определить допускаемую нагрузку из расчётов по допускаемым напряжениям и разрушающим нагрузкам и сравнить результаты.
4. Построить графики функций: N1(F), N2(F), dB(F); когда сила F возрастает от 0 до F = Fпр+ 0.
5. Изобразить на рисунке деформированное состояние системы.
Примечание: если в расчётной схеме задачи абсолютно жёсткий брус отсутствует, то подчёркнутое в тексте задачи пропускается, в противном случае пишется без подчерка.
Исходные данные
Шифр | l м | Aмм2 | sT МПа | EГПа | a0 град. | nТ |
31–6 | 1 | 240 | 250 | 200 | 20 | 1,6 |
Расчётная схема Решение
На расчётной схеме обозначим номера стальных тяг 1, 2, опорные реакции R1, R2, R3, R4 , точки С, G.
Значение силы FТ найдётся из условия
|si| = sT,
где si – нормальные напряжения в поперечных сечениях тяг, получаемые из «упругой» задачи. Для их определения сначала найдем опорные реакции R1, R2, затем продольные силы N1, N2.
В данной плоской упругой системе возникают 4 опорные реакции, в то время как для их определения имеются лишь 3 уравнения равновесия. Поэтому она является один раз статически неопределимой. Степень статической неопределимости определяется как разница 4 – 3 = 1.
Нет необходимости находить опорные реакции R3 и R4, так как они в дальнейших расчётах не применяются. Поэтому определим лишь R1 и R2. Составим уравнение равновесия. Но из всевозможных уравнений равновесия выберем равенство нулю суммы моментов относительно точки G, так как оно содержит именно те неизвестные опорные реакции R1, R2, которые необходимы в расчётах. Другие уравнения равновесия не составляем, так как они содержат R3, R4. Итак, имеем
å МG = 0, R1a+ R2cosa 2a – F 2a = 0.
Сократим на а и получим
R1+ 2R2cosa = 2F. (1)
К уравнению (1) необходимо добавить второе уравнение, содержащее те же неизвестные R1, R2. Для его составления покажем на рисунке деформированное состояние конструкции (пунктирные линии). Обозначим точки C΄, D. Ввиду малости деформаций перемещения BB΄, CC΄ считаются вертикальными, C΄D^CD, BB΄= Dl1, CD = Dl2. Из подобия треугольников GBB΄ и GCC΄ следует
Þ 2BB’=CC’ , т. е. 2D l1 = (2)
По закону Гука
Dl 1 =, Dl2 = .
Подставим в (2) и запишем
= или R2 = 2R1cosa. (3)
(1) и (3) образуют систему линейных алгебраических уравнений относительно R1 и R2. Решая, получим
R1 = R2 =
Обозначим
c1 = cos a = cos 20˚ = 0,9397, c2 = 2/(1 + 4 cos2a) = 2/(1 + 4· 0,93972) = 0,4413,
l1 = l / EA = 1 / 200 · 109 · 240 · 10-6 = 2,083 · 10-8 м / Н.
Найдём продольные силы:
N1 = R1 = Fc2, N2 = –R2 = –2Fc1c2 (4)
и перемещение точки B
dB = Dl 1 = = N1l1. (5)
Теперь можно найти формулы для нормальных напряжений в поперечных сечениях тяг:
s1 = N1/A = Fc2/A = 0,4413 F/A, s2 = N2/A = -2Fc1c2/A = — 0,8294 F/A. (6)
Из сравнения видно, что напряжение во второй тяге по абсолютному значению больше, чем в первой, т. е. | s2 | > s1, поэтому пластические деформации при возрастании силы F возникнут раньше во втором стержне. Найдём формулу для определения FТ. С этой целью приравняем большее из напряжений по модулю к пределу текучести материала
| s2 | = sT
или, что то же самое
0,8294 F/A = sT.
Отсюда
F = FТ = sTA / 0,8294 = 250 · 106 · 240 · 10-6 / 0,8294 = 72340 Н = 72,34 кН.
Этому значению нагрузки соответствуют продольные силы в тягах, определяемые формулами (4)
N1Т = 72,34 · 0,4413 = 31,92 кН, N2Т = — 2 · 72,34 · 0,9397 · 0,4413 = –60 кН
и перемещение точки B, вычисляемое формулой (5)
dBТ = N1Тl1 = 31920 · 2,083 ·10-8 = 0,665 · 10-3 м = 0,665 мм.
По значению силы FТ можно найти допускаемое значение:
[F]т = FТ / nТ = 72,34 / 1,6 = 45,21 кН.
Такой метод расчётов называется расчётом по допускаемым напряжениям. Второй и более точный метод расчётов – это расчёт по разрушающим нагрузкам (другое название – расчёт по несущей способности). Предельное состояние или исчерпание несущей способности системы наступит при достижении силой F предельного разрушающего значения, т. е. при F = Fпр, когда в обеих тягах напряжения будут равны пределу текучести sT:
s1 = sT, s2 = –sT.
Тогда продольные силы достигнут предельных значений т. е. оба стержня «потекут»:
N1пр = sT A = 250·106 · 240 · 10-6 = 60000 Н = 60 кН, N2пр = –sT A = –60 кН.
Здесь на рисунке стержни, в которых уже наступила текучесть, заштрихованы.
Найдём предельную нагрузку Fпр. Составим уравнение равновесия:
å МG = 0, N1пр а — N2пр c1 2а – Fпр2а = 0, 60 + 2 · 60 c1 = 2Fпр.
Отсюда
Fпр = 60 (1+2с1) / 2 =+ 2 · 0,9397) = 86,38 кН.
[F]пр = Fпр / nТ = 86,38 / 1,6 = 53,99 кН.
Разница результатов, полученных двумя методами расчётов на прочность, составляет
Перемещение dBпр = dB(Fпр – 0) вычисляется при F = Fпр – 0. Это означает, что вторая тяга уже «течёт», а первая продолжает оставаться в упругой стадии деформирования, хотя находится на «пределе», т. е. накануне текучести, так что N1 = 60 кН. К первой тяге ещё можно применять закон Гука. Следовательно,
dBпр = 60000 · 2,083 ·10-8 = 1,25 · 10-3 м = 1,25 мм.
По результатам вычислений построены графики функций (рис. 3, 4): N1(F), N2(F), dB(F); когда сила F возрастает от 0 до F = Fпр+ 0.

Рис. 3

Рис. 4
Исходные данные
Второе число шифра | l м | Aмм2 | sT МПа | EГПа | a град. | nт |
1 | 1,2 | 200 | 250 | 200 | 20 | 1,6 |
2 | 1,3 | 210 | 330 | 200 | 40 | 1,8 |
3 | 1,4 | 220 | 240 | 210 | 50 | 2,0 |
4 | 1,5 | 230 | 360 | 210 | 70 | 2,2 |
5 | 1,6 | 240 | 320 | 200 | 40 | 1,6 |
Расчётные схемы
| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 |
Источник

