Объемная деформация при одноосном растяжении
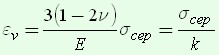
Объемным напряженным состоянием называют напряженное состояние, которое можно представить в виде трех ненулевых главных напряжений. Это напряженное состояние является общим случаем напряженного состояния тела в точке.
Обобщенный закон Гука
Напомним, что при одноосному растяжению или сжатию возникают деформации – продольные (в направлении действия силы) $varepsilon = sigma /E$ и поперечные (в двух других перпендикулярных направлениях) $varepsilon ‘ = — nu cdot varepsilon = — nu sigma /E$.
В случае действия трех главных напряжений ${sigma _1}$, ${sigma _2}$ и ${sigma _3}$ от каждого из них будут возникать продольные и поперечные деформации. Например, от напряжения ${sigma _2}$ будет возникать продольная деформация в направлении 2, которая равна ${varepsilon _2} = {sigma _2}/E$ и поперечные деформации в направлениях 1 и 3 ${varepsilon _1} = {varepsilon _3} = — nu cdot {sigma _2}/E$. Таким образом, деформации в направлении главных осей от системы трех главных напряжений будут определяться так
$begin{gathered} {varepsilon _1} = frac{1}{E}left( {{sigma _1} — nu ({sigma _2} + {sigma _3})} right) hfill \ {varepsilon _2} = frac{1}{E}left( {{sigma _2} — nu ({sigma _1} + {sigma _3})} right) hfill \ {varepsilon _3} = frac{1}{E}left( {{sigma _3} — nu ({sigma _1} + {sigma _2})} right) hfill \ end{gathered} $ – обобщенный закон Гука.
Объемная деформация. Объемный закон Гука
Определим изменение объема тела, которое находится в условиях объемного напряженного состояния.
Объем элементарного куба сторонами $dx$, $dy$ и $d$
${V_0} = dx cdot dy cdot d$.
После деформации, когда длина сторон куба изменилась на величину $Delta x$, $Delta y$ и $Delta z$, об’ем
[begin{gathered} {V_1} = (dx + Delta x) cdot (dy + Delta y) cdot (dz + Delta z) = hfill \ dx cdot dy cdot d + dx cdot dy cdot Delta z + dx cdot Delta y cdot d + underline {underline {dx cdot Delta y cdot Delta z} } + hfill \ + Delta x cdot dy cdot d + underline {underline {Delta x cdot dy cdot Delta z} } + underline {underline {Delta x cdot Delta y cdot d} } + underline {underline {underline {Delta x cdot Delta y cdot Delta z} } } hfill \ end{gathered} ]
Поскольку удлинения являются ничтожно малыми по сравнению с размерами элемента (например, $Delta x < < dx$), то в данной формуле можно пренебречь слагаемыми, которые являются бесконечно малыми второго и третьего порядка (подчеркнуты).
Абсолютное изменение о’объема
[Delta V = {V_1} — {V_0} = dx cdot dy cdot Delta z + dx cdot Delta y cdot d + Delta x cdot dy cdot d]
Относительное изменение о’объема
[{varepsilon _v} = frac{{Delta V}}{{{V_0}}} = frac{{dx cdot dy cdot Delta z + dx cdot Delta y cdot d + Delta x cdot dy cdot d}}{{dx cdot dy cdot d}} = frac{{Delta x}}{{dx}} + frac{{Delta y}}{{dy}} + frac{{Delta z}}{{d}} = {varepsilon _1} + {varepsilon _2} + {varepsilon _3}].
Если подставить вдносні деформации из обобщенного закона Гука, получим
[begin{gathered} {varepsilon _v} = {varepsilon _1} + {varepsilon _2} + {varepsilon _2} = frac{1}{E}left( {{sigma _1} — nu {sigma _2} — nu {sigma _3} + {sigma _2} — nu {sigma _1} — nu {sigma _3} + {sigma _3} — nu {sigma _1} — nu {sigma _2}} right) = hfill \ = frac{1}{E}left( {{sigma _1} + {sigma _2} + {sigma _3} — 2nu cdot left( {{sigma _1} + {sigma _2} + {sigma _3}} right)} right) = frac{{1 — 2nu }}{E}left( {{sigma _1} + {sigma _2} + {sigma _3}} right) hfill \ end{gathered} ]
[{varepsilon _v} = frac{{1 — 2nu }}{E}left( {{sigma _1} + {sigma _2} + {sigma _3}} right)] – об’емкий закон Гука.
Если среднее арифметическое значение главных напряжений ![]() , то объемный закон Гука можно записать так
, то объемный закон Гука можно записать так
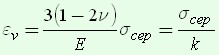 ,
,
где [k = frac{E}{{3left( {1 — 2nu } right)}}] – модуль объемной деформации, а
[{varepsilon _v} = frac{{{sigma _1} + {sigma _2} + {sigma _3}}}{k}].
Потенциальная энергия деформации
При деформации любого тела тратится определенное количество энергии, которая может превращаться в тепловую (при пластическом деформировании), или накапливаться внутри тела в виде внутренней энергии деформации (при упругом деформировании). В последнем случае при разгрузке тела эта накопленная внутренняя энергия выполняет работу.
Определим внутреннюю энергию, которая накапливается в стержне, растянутом силой $F$. Удлинение, которую приобретет стержень, определится по закону Гука
$Delta l = frac{{F cdot l}}{{EA}}$.
Работа, затраченные силой $F$ на перемещении $Delta l$, определяется как $F cdot Delta l$, но это справедливо только в случае, когда сила является неизменной в процессе удлинения стержня. На самом деле, значение силы изменяется от 0 до [F] пропорционально удлинению. Поэтому в случае деформирования тела работа, затраченные на деформирование, а вместе с ней и потенциальная энергия деформации будет определяться как
[U = frac{{F cdot Delta l}}{2} = frac{F}{2} cdot frac{{F cdot l}}{{EA}} = frac{{{F^2} cdot l}}{{2EA}}].
Удельная потенциальная энергия, которая накапливается в единице об’объема материала)
[u = frac{U}{V} = frac{{F cdot Delta l}}{{2 cdot A cdot l}} = frac{1}{2} cdot frac{F}{A} cdot frac{{Delta l}}{l} = frac{1}{2} cdot sigma cdot varepsilon = frac{{sigma cdot varepsilon }}{2} = frac{{{sigma ^2}}}{{2E}}].
В случае действия касательных напряжений аналогично
[u = frac{{tau cdot gamma }}{2} = frac{{{tau ^2}}}{{2G}}].
В случае о’объемного напряженного состояния
[begin{gathered} u = frac{{{sigma _1} cdot {varepsilon _1}}}{2} + frac{{{sigma _2} cdot {varepsilon _2}}}{2} + frac{{{sigma _3} cdot {varepsilon _3}}}{2} = hfill \ = frac{1}{{2E}}left( {{sigma _1} cdot left( {{sigma _1} — nu ({sigma _2} + {sigma _3})} right) + {sigma _2} cdot left( {{sigma _2} — nu ({sigma _1} + {sigma _3})} right) + {sigma _3} cdot left( {{sigma _3} — nu ({sigma _1} + {sigma _2})} right)} right) hfill \ end{gathered} ]
После упрощения имеем
[u = frac{1}{{2E}}left( {sigma _1^2 + sigma _2^2 + sigma _3^2 — 2nu cdot left( {{sigma _1}{sigma _2} + {sigma _2}{sigma _3} + {sigma _1}{sigma _3}} right)} right)].
При этом можно отдельно выделить потенциальную энергию, которая соответствует изменению о’объема тела
![]()
и изменении формы тела
![]() .
.
Зависимости между модулем упругости E и модулем сдвига G
Рассмотрим частный случай плоского напряженного состояния – чистый сдвиг, при котором на некоторых площадках возникают только касательные напряжения [tau ]. Ранее показано, что при чистом сдвиге главными площадками являются площадки, которые находятся под углом 45 в рассматриваемых. Главные напряжения при этом
[begin{gathered} {sigma _1} = tau hfill \ {sigma _2} = 0 hfill \ {sigma _3} = — tau hfill \ end{gathered} ]
Тогда потенциальная энергия деформации
[u = frac{1}{{2E}}left( {tau _{}^2 + 0 + tau _{}^2 — 2nu cdot left( {0 + 0 — {tau ^2}} right)} right) = frac{{2 + 2nu }}{{2E}}{tau ^2} = frac{{1 + nu }}{E}{tau ^2}].
Если рассмотреть ту же самую энергию на площадках, где возникают только касательные напряжения, то
[u = frac{{{tau ^2}}}{{2G}}].
Отсюда [frac{{1 + nu }}{E}{tau ^2} = frac{{{tau ^2}}}{{2G}}], то есть между модулем упругости E, модулем сдвига G и коэффициентом Пуассона $nu$ существует взаимозависимость
[G = frac{E}{{2left( {1 + nu } right)}}]
которая справедлива для всех изотропных материалов (материалов, деформівні свойства которых одинаковы во всех направлениях).
Источник
Различают: абсолютные деформации — это изменение размеров бруса до и после деформации, (удлинение , сужение ); относительные деформации — это отношение абсолютной деформации к первоначальной длине, (продольная деформация , поперечная деформация ).
Между относительными деформациями установлена связь в виде коэффициента Пуассона.
Коэффициент Пуассона показывает во сколько раз продольная деформация больше поперечной. Для изотропных материалов может принимать значения от 0 до 0,5 ( 0 – пробка, 0,3 – сталь, 0,5 – резина)
Между нагрузкой и удлинением английский ученый Роберт Гук установил прямо пропорциональную зависимость, которую впоследствии оформили в виде выражения и назвали законом Гука :В пределахупругих деформаций нормальные напряжения при одноосном растяжении, сжатии прямо пропорциональны относительной продольной деформации. Коэффициент пропорциональности Е называется модулем продольной упругости или модулем Юнга, он характеризует жесткость материала, т.е. способность сопротивляться упругим деформациям (сталь — 2·105 МПа, медь — 1·105 МПа, резина – 5 МПа)
Коэффициент Пуассона и модуль продольной упругости – это упругие постоянные материала. определяются в лабораторной работе.
Механические свойства материалов:
— Характеристики прочности:
— предел пропорциональности σПЦ – это напряжение, до которого справедлив закон Гука;
— предел текучести σТ – это напряжение, при котором происходит рост пластических деформаций при практически постоянной нагрузке;
— предел прочности (временное напряжение) σПЧ, (σВ)– это условное напряжение, соответствующее максимальной нагрузке, выдерживаемой образцом до разрушения.
— Характеристики пластичности:
— относительное удлинение ,
— относительное сужение .
Характеристики прочности и пластичности определяются в лабораторной работе.
Условие прочности:
— по коэффициенту запаса —Прочность элемента конструкции обеспечена, если рабочий коэффициент запаса не ниже допускаемого.
— по опасной точке или —Прочность элемента конструкции обеспечена, если максимальное рабочее напряжение не превышает допускаемое напряжение.
Виды расчетов и их цели:
— проверочный– проверить прочность спроектированного элемента конструкции:
— проектный —определить геометрические размеры проектируемого элемента конструкции:
— определение допускаемой нагрузки.
Условие прочности при растяжении, сжатии и виды расчетов:
,
где — допускаемое напряжение, — предельное напряжение (пластичный материал — = , хрупкий материал = ), — допускаемый коэффициент запаса прочности.
1. Проверочный
2. Проектный
3. Определение допускаемой нагрузки
Задача 1.
1.1 Для стального стержня постоянного поперечного сечения (А = см2):
а) построить эпюру продольных сил (рис.1) Продольные силы на участках:
N1 =
N2 =
N3 =
N4 =
Рис.1 Расчетная схема стержня и эпюра продольных сил
б) определить опасный участок и напряжение на нем.
Примечание: Опасный участок это участок с максимальной нагрузкой или максимальным напряжением. В данной задаче опасный участок Nmax =
Напряжение на опасном участке
в) определить удлинение стального (Е = 2٠10 5 МПа) стержня
1.2 Для стального стрежня (Е = 2٠10 5 МПа) непостоянного поперечного сечения:
а) Продольные силы на участках:
N1 =
N2 =
N3 =
МПа
Рис.2 Расчетная схема стержня и эпюры продольных сил и нормальных напряжений
б) Напряжения на участках:
в) Опасный участок: max =
г) Удлинение
Задача 2. Проверить прочность стержня диаметром d = 10 мм, нагруженного растягивающими силами F = 10 кН, если допускаемое напряжение [σ] = 100 МПа.
Вид расчета — проверочный
Расчетная формула
N =F =
;
Вывод:
Задача 3. Определить диаметр стержня, нагруженного растягивающей силой F = 10 кН, если допускаемое напряжение [σ] = 100 МПа.
Вид расчета – проектный
Расчетная формула =
N =F =
;
Задача 4. Определить допускаемую растягивающую нагрузку F на стержень диаметром d = 10 мм, если допускаемое напряжение [σ] = 100 МПа.
Вид расчета – определение допускаемой нагрузки
Расчетная формула = =
Источник
Возьмём однородный стержень и приложим к его основаниям растягивающие (или сжимающие) усилия (рис.7.1). Пусть — длина недеформированного стрежня, а S — его сечение. После приложения силы F его длина получает приращение D и делается равной . Отношение
, (7.1)
называется относительным удлинением стержня.
В случае растягивающих сил оно положительно, в случае сжимающих сил – отрицательно.
Деформация стержня связана с возникновением упругих сил, с которыми одна часть стержня действует на другую, с которой она граничит. Такие силы действуют в любом поперечном сечении. Внешняя сила, приложенная к каждой из этих двух частей, уравновешивается упругой силой Fупр, действующей на рассматриваемую часть со стороны другой. Силу, перпендикулярную поперечному сечению стержня и отнесенную к единице его площади, называют нормальным упругим напряжением
. (7.2)
В системе СИ упругое напряжение измеряется в Н/м2 .
Опыт показывает, что при малых деформациях, возникающие в теле нормальные упругие напряжения пропорциональны относительной деформации, т.е.
, (7.3)
где Е — постоянная, называемая модулем Юнга и зависящая только от материала стержня и его физического состояния..
Формула (7.3) выражает закон Гука для деформации растяжения и сжатия. Из нее следует, что модуль Юнга равен тому нормальному напряжению, при котором относительное удлинение равно единице. Длина стержня в этом случае увеличилась бы в 2 раза, если бы при такой деформации выполнялся закон Гука. Однако, при таких больших деформациях закон Гука не выполняется и либо образец разрушается, либо нарушается пропорциональность между деформацией и силой.
Под действием растягивающей или сжимающей силы изменяются не только продольные, но и поперечные размеры стержня. Характеристикой этого изменения является относительное поперечное сжатие (растяжение)
, (7.4)
где d — поперечный размер образца.
При растяжении e i < 0, при сжатии e i>0. Отношение
, (7.5)
называется коэффициентом Пуассона.
Для большинства изотропных материалов, к которым относятся, например, металлы, имеющие поликристаллическую структуру, он близок к 0,25. Модуль Юнга Е и коэффициент Пуассона m полностью характеризуют упругие свойства изотропного материала. Все прочие упругие постоянные могут быть выражены через Е и m.
Деформированное тело обладает запасом потенциальной энергии.Эта энергия называетсяупругой. Она равна работе, затраченной на деформацию тела.
Приложим к стержню растягивающую силу ƒ(x) и будем непрерывно увеличивать ее от начального значения ƒ=0 до конечного значения ƒ=F. При этом удлинение будет меняться от x = 0 до конечного значения x = Dl. По закону Гука
. (7.6)
Вся работа, совершаемая при деформации, запасается в виде упругой энергии, поэтому
. (7.7)
Эта энергия распределена по всему объему деформированного тела, что дает основание ввести плотность энергии упругой деформации, т.е. энергию, приходящуюся на единицу объема стержня,
. (7.8)
Сдвиг
Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости, называемой плоскостью сдвига, смещаются параллельно друг другу (рис.7.2). Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АD, параллельная ВС, закреплена неподвижно. При малом сдвиге:
, (7.9)
где D х = — абсолютный сдвиг, а g — угол сдвига, называемый также относительным сдвигом.
В любом сечении образца, параллельном плоскости сдвига, возникают уже не нормальные, а касательные упругие напряжения, определяемые по формуле
. (7.10)
По закону Гука касательные напряжения пропорциональны относительному сдвигу,т.е.
, (7.11)
где G — модуль сдвига.
Модуль сдвига численно равен тому касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном единице, если бы в этом случае выполнялся закон Гука.
Между модулем сдвига, модулем Юнга и коэффициентом Пуассона существует следующее соотношение
. (7.12)
Объемная плотность энергии упругой деформации при сдвиге, как и при растяжении (7.8), прямо пропорциональна квадрату напряжения и обратно пропорциональна модулю упругости:
. (7.13)
Кручение
Возьмем однородный стержень, закрепим его верхний конец, а к нижнему концу приложим закручивающие силы, создающие вращающий момент. В результате этого каждый радиус нижнего основания повернется вокруг продольной оси на некоторый угол. Такая деформация называется кручением.
Деформация кручения является неоднородной. Это значит, что деформация внутри образца меняется от точки к точке. Чем дальше от оси вращения, тем больше деформация.
Закон Гука для деформации кручения записывается в виде
, (7.14)
где ƒ – постоянная для данного образца величина, называемая модулем кручения, — угол кручения, — крутящий момент.
Модуль кручения показывает, какой момент сил нужно приложить, чтобы закрутить стержень на угол в 1 рад. В отличие от модулей Юнга и сдвига он зависит не только от материала, но и от геометрических размеров образца.
Деформацию кручения можно свести к деформации сдвига. Выведем выражение для модуля кручения.
Стержень (рис.7.3) можно представить состоящим из множества цилиндрических оболочек (трубок) радиусом r, длиной L и толщиной dr. Площадь основания трубки
dS = 2p rdr , (7.15)
а момент упругих сил, действующих на это основание:
dM = 2 p r dr τ r , (7.16)
где τ — тангенциальное напряжение в этом основании.
С учетом того, что каждый элемент цилиндрической трубки сдвигается на угол:
, (7.17)
то по закону Гука для деформации сдвига получим
. (7.18)
Таким образом, момент сил, действующих на цилиндрическую трубку, равен
. (7.19)
Полный момент сил, действующих на стержень радиуса R, найдется интегрированием:
. (7.20)
Сопоставляя (7.20) с законом Гука для деформации кручения (7.14), получим выражение для модуля кручения:
. (7.21)
Экспериментально модуль кручения можно измерить. С этой целью подвесим на проволоке массивное симметричное телои возбудим крутильные колебания. Эти колебания будут гармоническими с периодом
, (7.22)
где I – момент инерции тела, f – модуль кручения проволоки. Если момент инерции тела известен, то, определив период колебаний, можно вычислить по формуле (9.22) модуль кручения проволоки.
Примеры решения задач
1. Нижнее основание стального цилиндра диаметром d=20 см и высотой h=20 см закреплено неподвижно. На верхнее основание действует горизонтальная сила F=20 кН. Найти: 1) тангенциальное напряжение в материале цилиндра, 2) смещение верхнего основания цилиндра, 3) потенциальную энергию и объемную плотность деформированного образца.
Решение
1) Тангенциальное напряжение материала деформированного образца выражается формулой
.
В данном случае , поэтому получим
.
Сделав вычисления, найдем
2) Смещение верхнего основания цилиндра будет равно
,
где — угол сдвига.
В соответствии с законом Гука
,
где = 8,1.1010 Па — модуль сдвига стали.
Произведя подстановку, получим
.
Выполнив вычисления, найдем
1,6 мкм.
3. Потенциальная энергия и объемная плотность энергии деформированного образца определятся по формулам
и .
Сделав вычисления, получим, U=159 мДж, w= 2,5 Дж/м3.
2. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа А=6,9 Дж. Длина стержня l=1 м, площадь поперечного сечения S=1 мм2, модуль Юнга для алюминия Е=69 ГПа.
Решение
Работа, затраченная при растяжении стержня, переходит в его упругую потенциальную энергию
,
где — нормальное напряжение деформированного образца, V =Sl – его объем.
В соответствии с законом Гука
.
После подстановки и преобразований, найдем
.
Вычисления дают
Основные положения
1. Упругое напряжение – физическая величина, равная упругой силе, приходящейся на единицу площади:
— нормальное напряжение, сила направлена по нормали к площадке
;
— тангенциальное напряжение, сила направлена по касательной к площадке
.
2. Закон Гука – напряжение упруго деформированного тела прямо пропорционально его относительной деформации:
— деформация растяжения (сжатия)
;
— деформация сдвига
.
3. Коэффициент Пуассона – отношение поперечного сужения к продольному удлинению:
4. Объемная плотность энергии упруго деформированного тела:
— деформация растяжения (сжатия)
;
— деформация сдвига
.
Контрольные вопросы
1. Что такое упругие напряжения? Как определяются нормальные и тангенциальные напряжения?
2. Как формулируется закон Гука для различных видов деформации?
3. Каков физический смысл модуля Юнга и модуля сдвига?
4. Как определяется коэффициент Пуассона?
5. От чего зависит объемная плотность энергии упруго деформированного тела?
Механика жидкостей и газов
Источник
