Нейтральная линия при внецентренном растяжении
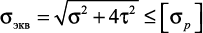
Внецентренное растяжение (сжатие) вызывается силой, параллельной оси бруса, но не совпадающей с ней (рис. 10.6).
Рис. 10.6.
Внецентренное растяжение (сжатие) может быть сведено к осевому растяжению (сжатию) и косому изгибу, если перенести силу P в центр тяжести сечения. Внутренние силовые факторы в произвольном поперечном сечении бруса равны:
, | (10.13) |
где yp, zp — координаты точки приложения силы.
На основании принципа независимости действия сил напряжения в точках поперечного сечения при внецентренном растяжении (сжатии) определяются по формуле:
(10.14) |
или
, | (10.15) |
где — радиусы инерции сечения.
Выражение в скобках в уравнении (10.15) показывает во сколько раз напряжения при внецентренном растяжении (сжатии) больше напряжений центрального растяжения.
Уравнение нейтральной линии определяем из (10.15), приравнивая правую часть (10.15) нулю. После сокращения на P/F получим
. | (10.16) |
Таким образом, нейтральная линия при внецентренном растяжении (сжатии) не проходит через центр тяжести сечения. Нейтральная линия отсекает на осях координат отрезки
. | (10.17) |
Из формулы (10.17) видно, что точка приложения силы и нейтральная линия всегда расположены по разные стороны от центра тяжести сечения, причем положение нейтральной линии определяется координатами точки приложения силы (рис. 10.7).
При приближении точки приложения силы к центру тяжести сечения (a и b по абсолютной величине возрастают) нейтральная линия будет удаляться от центра. При этом в сечении увеличивается доля напряжений одного знака, так как уменьшаются напряжения от изгиба. При удалении точки приложения силы от центра тяжести сечения (a и b по абсолютной величине убывают) нейтральная линия будет приближаться к центру. При этом в сечении увеличивается доля напряжений разного знака, так как возрастают напряжения от изгиба. В пределе при a=b=0 нейтральная линия удаляется в бесконечность. В этом случае будет иметь место центральное растяжение (сжатие) бруса.
Всегда можно найти такое положение точки приложения силы, при котором нейтральная линия будет касаться контура сечения, нигде не пересекая его. В этом случае в сечении напряжения будут только одного знака. Зона вблизи центра тяжести сечения, приложение продольной нагрузки в которой вызывает появление во всех точках сечения напряжений только одного знака, называется ядром сечения. До тех, пока точка приложения силы находится внутри ядра, нейтральная линия не пересекает контур сечения и напряжения во всем сечении будут одного знака. Если точка приложения силы расположена вне ядра, то нейтральная линия пересекает контур сечения, и тогда в сечении будут действовать напряжения разного знака. Указанное обстоятельство необходимо учитывать при расчете элементов конструкций из хрупких материалов, плохо воспринимающих растягивающие нагрузки. В этом случае необходимо прикладывать внешние силы так, чтобы во всем сечении действовали только напряжения сжатия. Для этого точка приложения равнодействующей внешних сил должна находиться внутри ядра сечения.
Рис. 10.7.
Расчет на прочность при внецентренном растяжении (сжатии) производится так же, как и при косом изгибе, — по нормальному напряжению в опасной точке поперечного сечения. Опасной является точка сечения, наиболее удаленная от нейтральной линии. Однако, в тех случаях, когда в этой точке действует напряжение сжатия, а материал элемента конструкции хрупкий, опасной может быть точка, в которой действует наибольшее растягивающее напряжение. Эпюра напряжений строится на оси, перпендикулярной к нейтральной линии сечения и ограничена прямой линией. Условие прочности имеет следующий вид:
, | (10.18) |
где yA,zA — координаты опасной точки, а [σ] — допускаемое напряжение на растяжение и сжатие.
Источник
Лекция 15. ВНЕЦЕНТРЕННОЕ СЖАТИЕ
Внецентренное сжатие. Построение ядра сечения. Изгиб с кручением. Расчеты на прочность при сложном напряженном состоянии.
Внецентренное сжатие – это вид деформации, при котором продольная
сила в поперечном сечении стержня приложена не в центре тяжести. При
внецентренном сжатии, помимо продольной силы (N), возникают два
изгибающих момента (Mx и My).
Считают, что стержень обладает большой жесткостью на изгиб, чтобы пренебречь прогибом стержня при внецентренном сжатии.
Преобразуем формулу моментов при внецентренном сжатии 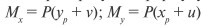 , подставляя значения изгибающих моментов:
, подставляя значения изгибающих моментов:
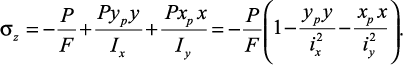
Обозначим координаты некоторой точки нейтральной (нулевой) линии
при внецентренном сжатии xN, yN и подставим их в формулу нормальных
напряжений при внецентренном сжатии. Учитывая, что напряжения в точках
нейтральной линии равны нулю, после сокращения на P/F, получим уравнение
нейтральной линии при внецентренном сжатии:
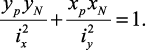 (35)
(35)
Нулевая линия при внецентренном сжатии и точка приложения нагрузки
всегда расположены по разные стороны от центра тяжести сечения.
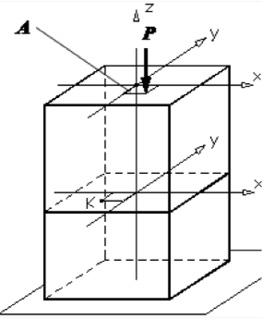
Рис. 43. Внецентренное сжатие
Отрезки, отсекаемые нулевой линией от осей координат, обозначенные
ax и ay, легко найти из уравнения нулевой линии при внецентренном
сжатии. Если сначала принять xN = 0, yN = ay, а затем принять yN = 0,
xN = ax, то найдем точки пересечения нулевой линии при внецентренном
сжатии с главными центральными осями:
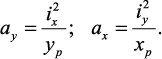
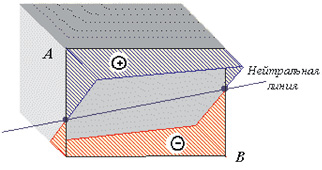
Рис. 44. Нейтральная линия при внецентренном растяжении – сжатии
Нейтральная линия при внецентренном сжатии разделит поперечное
сечение на две части. В одной части напряжения будут сжимающими,
в другой – растягивающими. Расчет на прочность, как и в случае косого
изгиба, проводят по нормальным напряжениям, возникающим в опасной точке
поперечного сечения (наиболее удаленной от нулевой линии).
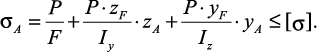 (36)
(36)
Ядро сечения – малая область вокруг центра тяжести поперечного
сечения, характерная тем, что любая сжимающая продольная сила,
приложенная внутри ядра, вызывает во всех точках поперечного сечения
сжимающие напряжения.
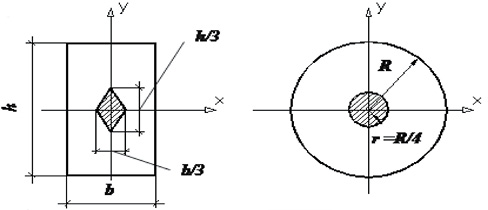
Примеры ядра сечения для прямоугольного и круглого поперечных сечений стержня.
а б
Рис. 45. Форма ядра сечения для прямоугольника и круга
Изгиб с кручением. Такому нагружению (одновременному действию
крутящих и изгибающих моментов)часто подвержены валы машин и механизмов.
Для расчета бруса необходимо прежде всего установить опасные сечения.
Для этого строятся эпюры изгибающих и крутящих моментов.
Используя принцип независимости действия сил, определим напряжения, возникающие в брусе отдельно для кручения, и для изгиба.
При кручении в поперечных сечениях бруса возникают касательные
напряжения, достигающие наибольшего значения в точках контура сечения 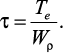
При изгибе в поперечных сечениях бруса возникают нормальные напряжения,
достигающие наибольшего значения в крайних волокнах бруса 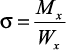 .
.
Касательные напряжения значительно меньше напряжений от крутящего
момента, поэтому ими пренебрегают. Опасное сечение бруса будет
у заделки, где действуют максимальные напряжения от изгиба и кручения.
Исследуем напряженное состояние в наиболее опасной точке A
(рис. 46). Так как напряженное состояние двухосное, то для проверки
прочности применяем одну из гипотез.
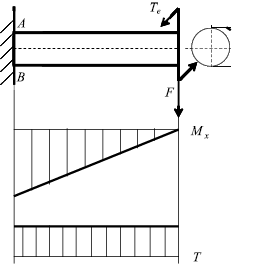
Рис. 46. Эпюры изгибающих и крутящих моментов
Применяя третью теорию прочности
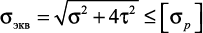
и учитывая, что 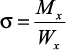 и
и 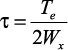 , получаем:
, получаем:
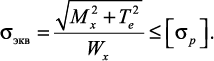
Для подбора сечения находим требуемый момент сопротивления
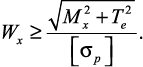
Источник
Ранее мы изучали случай простого (центрального) растяжения и сжатия, когда внешние силы прикладывались в центре тяжести поперечных сечений.
Однако в практике встречаются случаи внецентренного приложения растягивающей или сжимающей нагрузки, как показано на рис. 7.11.

Рис. 7.11. Внецентренное сжатие стержня
Здесь величина е — эксцентриситет нагрузки. Сжатие стержней может вызвать потерю устойчивости, анализ которой необходимо также делать и при расчетах на прочность, однако ограничимся пока рассмотрением элементов конструкций, которые не подвержены потере устойчивости. Это стержни большой жесткости или массивные стержни.
Пусть оси х и у — главные центральные оси инерции сечения. Приведем внешние силы Г к центру тяжести сечения. Для этого на краях стержня в точках на оси стержня, проходящих через точку О, мысленно приложим осевые противоположно направленные силы Г. Тогда силы, векторы которых зачеркнуты одной косой чертой, дадут момент в плоскости под углом к главным осям. А это значит, что вне-центренное растяжение (сжатие) приводится к центральному растяжению (сжатию) и косому изгибу. Найдем внутренние силовые факторы в сечении а—а (см. рис. 7.11), для чего используем метод сечений. Рассмотрим равновесие отсеченной нижней части стержня. После приведения силы Т7к центру тяжести сечения получим следующие внутренние силовые факторы: Nz = -Р — продольная сжимающая сила; Мх = Ру/г и Му = Рхг — изгибающие моменты, где уР ихг—координаты точки приложения силы Р.
Выведем рабочие формулы для расчета на прочность массивных стержней при вненентренном растяжении (сжатии) (рис. 7.12).

Рис. 7.12. Приложение внеценгренной нагрузки к стержню: а — расчетная схема; б — равновесие части стержня
Найдем внутренние силовые факторы в произвольном сечении, находящемся на расстоянии I от свободного края, для чего используем метод сечений. Рассмотрев равновесие оставленной части стержня (рис. 7.12, б), можно увидеть, что он испытывает растяжение совместно с двумя изгибами:
ЛД =-Р ; Мх = /г/г/2 ; Му =-РЬ/2 .
Если бы сила /’лежала в одной из главных плоскостей, то она вызвала бы сжатие с прямым изгибом.
Для определения напряжения в любой точке поперечного сечения необходимо использовать ранее выведенные формулы для сжатия (растяжения) и простого плоского изгиба, а также иметь в виду справедливость принципа независимости действия сил.
Например, в точке А сечения (см. рис. 7.12, б) все три внутренних силовых фактора вызовут напряжения одного знака, поэтому должны суммироваться:
=-М,/А-Мх^х-Му^у = -Р/А-[(РИ/2)/ІУх]-[(РЬ/2)/1?г]
ИЛИ
а =-Р/_РхРх/ _Ругу/ =_/г

У
+ +
/ Г / I
к /у / х;
,(7.10)

и г* — так называемые радиусы инерции по
перечного сечения.
Как и при косом изгибе, найдем опасные точки в сечении, для чего прежде всего найдем положение нейтральной линии.
Условие для нейтральной линии можно записать в виде о = 0. Координаты точек нейтральной линии — х0, >>0. После подстановки в формулу (7.10) получим

Но У/Л Ф 0, тогда
- (7.П)
- 1 + хгхо/2 + урУу = 0 . іу Л2
Это и есть уравнение нейтральной линии, представляющей собой уравнение прямой в отрезках (т.е. линии, не проходящей через начало координат).
Определим положение нейтральной линии. Полагая в (7.11) *о = 0, у0 = получим отрезок ау и, полагая х0 = ах, = 0, получим отрезок ах:




(7.12)
Полученные отрезки ах и ау представляют собой отрезки, отсекаемые нейтральной линией на координатных осях. Таким образом, нейтральная линия проходит за центром тяжести сечения от точки приложения силы.
Части сечения, расположенные по разные стороны от нейтральной линии, испытывают напряжения разного знака. Если провести прямые линии, параллельные нейтральной оси и так, чтобы они касались контура поперечного сечения, то мы найдем опасные точки. Напряжения в этих точках можно определить, используя формулу (7.10), если подставить сюда координаты найденных опасных точек.
Максимальное напряжение, необходимое для составления условия прочности для материала, одинаково работающего на растяжение и сжатие, получится при подстановке в (7.10) координат наиболее удаленной от нейтральной оси опасной точки.
Если материал хрупкий, то расчет ведется как по наибольшим растягивающим напряжениям, так и по наибольшим сжимающим напряжениям.
В том случае, когда сила Е приложена центрально, нейтральная линия находится в бесконечности и напряжения в поперечном сечении распределены равномерно. По мере того как точка приложения силы удаляется от центра тяжести, нейтральная линия приближается к центру тяжести. Из сказанного следует, что нейтральная ось может находиться за контуром поперечного сечения. Этот вывод полезен при расчетах конструкций, плохо работающих на растяжение, например кирпичных, каменных или бетонных колонн. Желательно, чтобы эти конструкции вообще не испытывали растягивающих напряжений. Это требование можно выполнить, если нейтральная линия в крайнем случае только касается контура поперечного сечения.
На рис. 7.13, а показаны различные положения нейтральных линий и соответствующие им точки приложения силы Т. Если же непрерывно «перемещать» по контуру нейтральную линию, то получится непрерывная линия вокруг центра тяжести поперечного сечения, определяющая геометрическое место точек приложения силы Р. Эта линия ограничивает некоторую зону, которая называется ядром сечения.
Таким образом, получается, что приложенные силы в точке ядра сечения не вызывают появления в поперечном сечении напряжений различных знаков. Если поперечное сечение стержня имеет контур с внутренними углами или отрицательную кривизну, то для определения точек ядра сечения надо обходить эти места, как показано на рис. 7.13, а.

Рис. 7.13. Определение ядра сечения
Для определения точек ядра сечения можно воспользоваться формулами (7.12). Рассмотрим, например, как определить ядро сечения для случая прямоугольного поперечного сечения (рис. 7.14).

С
I
і
1
I



Рис. 7.14. Определение ядра сечения для случая прямоугольного
поперечного сечения

- 2. Повернем нейтральную ось в положение II—II, т.е.
- 1. Проведем нейтральную ось по контуру в положение 1-І, тогда:


= оо
В этом случае:

При переходе из положения 1—1 в положение II—II нейтральная ось вращается в вершине прямоугольника, в это время точка приложения сосредоточенной силы перемещается по прямой 1-2. Аналогично находят другие точки ядра сечения.
Контрольные вопросы
- 1. Какой вид изгиба называется косым?
- 2. В чем отличие косого изгиба от прямого?
- 3. Как найти положение нейтральной линии сечения при косом изгибе?
- 4. Определение нормальных напряжений при косом изгибе.
- 5. Как определяются максимальные напряжения при изгибе с растяжением (сжатием)? Как найти опасную точку сечения?
- 6. Проходит ли нейтральная линия сечения через его центр тяжести при изгибе с растяжением (сжатием)?
- 7. Что такое внецентренное растяжение (сжатие)?
- 8. Положение нейтральной оси при внецентренном растяжении (сжатии).
- 9. Как найти опасные точки (точку) при внецентренном растяжении?
- 10. Как записываются условия прочности при изгибе с растяжением (сжатием)?
- 11. Что такое ядро сечения? Показать построение ядра сечения на примере прямоугольного сечения.
Источник
Внецентренное растяжение (сжатие) вызывается силой, параллельной оси бруса, но не совпадающей с ней (рис. 9.4).
Проекция точки приложения силы на поперечное сечение называется полюсом или силовой точкой, а прямая, проходящая через полюс и центр сечения, — силовой линией.
Внецентренное растяжение (сжатие) может быть сведено к осевому растяжению (сжатию) и косому изгибу, если перенести силу Р в центр тяжести сечения. Так, сила Р, отмеченная на рис. 9.4 одной черточкой Г вызовет осевое растяжение бруса, а пара сил, отмеченных двумя черточками, — косой изгиб.
Рис. 9.4
На основании принципа независимости действия сил напряжения в точках поперечного сечения при внецентренном растяжении (сжатии) определяются по формуле
В эту формулу осевую силу изгибающие моменты а также координаты точки сечения, в которой определяется напряжение, надо подставлять с их знаками. Для изгибающих моментов примем такое же правило знаков, как и при косом изгибе, а осевую силу будем считать положительной, когда она вызывает растяжение.
Если координаты полюса обозначить через , то момент Формула (9.5) принимает вид
Из этого уравнения видно, что концы векторов напряжений в точках сечения расположены на плоскости. Линия пересечения плоскости напряжений с плоскостью поперечного сечения является нейтральной линией, уравнение которой находим, приравнивая правую часть равенства (9.6) нулю. После сокращения на Р получим
откуда
Таким образом, нейтральная линия при внецентренном растяжении (сжатии) не проходит через центр тяжести сечения и не перпендикулярна плоскости действия изгибающего момента. Нейтральная линия отсекает на осях координат отрезки
Представим моменты инерции как произведения площади сечения на квадрат соответствующего радиуса инерции
Тогда выражения (9.8) можно записать так:
Из формул (9.8) видно, что полюс и нейтральная линия всегда расположены по разные стороны от центра тяжести сечения, причем положение нейтральной линии определяется координатами полюса.
Рис. 9.5
Рис. 9.6.
При приближении полюса по силовой линии к центру тяжести сечения нейтральная линия будет удаляться от центра, оставаясь параллельной своему первоначальному направлению. В пределе при нейтральная линия удалится в бесконечность. В этом случае будет иметь место центральное растяжение (сжатие) бруса.
На силовой линии всегда можно найти такое положение полюса, при котором нейтральная линия будет касаться контура сечения, нигде не пересекая его. Если провести все возможные нейтральные линии так, чтобы они касались контура сечения, нигде не пересекая его, и найти соответствующие им полюсы, то окажется, что полюсы будут расположены на вполне определенной для каждого сечения замкнутой линии. Область, ограниченная этой линией, называется ядром сечения. В круглом сечении, например, ядро представляет собой круг диаметром в 4 раза меньшим диаметра сечения, а в прямоугольных и двутавровых сечениях ядро имеет форму параллелограмма (рис. 9.5).
Из самого построения ядра сечения следует, что до тех пор, пока полюс находится внутри ядра, нейтральная линия не пересечет контур сечения и напряжения во всем сечении будут одного знака. Если, же полюс расположен вне ядра, то нейтральная линия пересечет контур сечения, и тогда в сечении будут действовать напряжения разного знака. Указанное обстоятельство необходимо учитывать при расчете на виецентренное сжатие стоек из хрупких материалов. Поскольку хрупкие материалы плохо воспринимают растягивающие нагрузки, то желательно внешние силы прикладывать к стойке так, чтобы во всем сечении действовали только напряжения сжатия. Для этого точка приложения равнодействующей внешних сил, сжимающих стойку, должна находиться внутри ядра сечения.
Расчет на прочность при внецентренном растяжении и сжатии производится так же, как и при косом изгибе, — по напряжению в опасной точке поперечного сечения. Опасной является точка сечения, наиболее удаленная от его нейтральной линии. Однако в тех случаях, когда в этой точке действует напряжение сжатия, а материал стойки хрупкий, опасной может быть точка, в которой действуй наибольшее растягивающее напряжение.
Эпюра напряжений строится на оси, перпендикулярной к нейтральной линии сечения, и ограничена прямой линией (см. рис. 9,4).
Условие прочности запишется так:
Здесь — координаты опасной точки, а — допускаемое напряжение на растяжение или сжатие.
Пример. Определить, во сколько раз напряжение в опасной точке бруса прямоугольного сечения при внецентренном приложении нагрузки больше, чем при центральном ее приложении (рис. 9.6).
Решение. При центральном приложении нагрузки напряжения во всех точках поперечных сечений стойки одинаковы.
При внецентренном приложении нагрузки в поперечных сечениях стойки действуют осевая сила и изгибающие моменты и Подставляя в формулу (9.7) значения силовых факторов и моментов инерции, находим уравнение нейтральной линии:
Наиболее удалена от нейтральной линии точка А с координатами и Напряжение в этой точке
Итак, напряжение в опасной точке, при внецентренном приложении силы Р оказалось в семь раз больше, чем при центральном ее приложении. Этот результат показывает, насколько важно для уменьшения напряжений обеспечивать центральное приложение нагрузки.
Источник
