Напряжения при растяжении пластины

Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Растяжение пластины с отверстиями
[c.230]
РАСТЯЖЕНИЕ ПЛАСТИНЫ С ОТВЕРСТИЯМИ
[c.233]
При одноосном растяжении пластины с отверстием в форме астроиды (см. рис. ПЗО) в направлении оси симметрии, проходящей через пару точек возврата, имеем [ ]
[c.539]
Аналогичное явление концентрации напряжений имеет место при растяжении пластины с отверстием в центре. В случае круглого отверстия (рис. 5, Ь), диаметр которого мал по сравнению с шириной пластины (a/d>5), максимальные растягиваюш,ие напряжения в точках т и п по краям отверстия в три раза больше напряжения,
[c.563]
Для анизотропных при упругой деформации материалов следует учитывать зависимость концентрации напряжений от направления нагружения. Так, для фанеры с отношением модулей упругости вдоль и поперек волокон 2.1, при растяжении пластины с отверстием коэффициент концентрации при нагружении вдоль волокон равен 5,45, а поперек — 4,15 [6].
[c.100]
При растяжении пластин с двумя симметричными выточками (см. рис. 10, а), как и при растяжении пластин с отверстием, происходит смещение максимума осевых растягивающих напряжений от дна выточки в тело пластины.
[c.557]
Растяжение пластины с отверстием (см, фнг, 412, в). Наибольшее
[c.625]
При растяжении пластины с отверстием (риг 10) в качестве номинального напряжения принимают
[c.21]
ОДНООСНОЕ РАСТЯЖЕНИЕ ПЛАСТИНЫ С ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ
[c.321]
ВСЕСТОРОННЕЕ РАСТЯЖЕНИЕ ПЛАСТИНЫ с ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ
[c.323]
При т = О имеет место случай всестороннего растяжения пластины с круговым отверстием по формуле (9.434) получим величину (оее)гаах = 2о, совпадающую с результатом формулы (9.331) при г =а = а.
[c.324]
Предположим, что в рассмотренных задачах о растяжении пластины с эллиптическим отверстием интенсивность усилий а фиксирована, а параметр эллиптического отверстия /п 1, т. е. отверстие вырождается в прямолинейную щель длиной 4 по оси Oxi (см. 27 данной главы). В этом случае напряжение 099 на концах щели (в точках А, см. рис. 9.51) согласно формулам (9.430) и (9.434) неограничено возрастает при любом конечном значении а как при одноосном, так и при всестороннем растяжении пластины.
[c.324]
Согласно уравнению (7.18), эти зависимости изображаются пучком прямых, проходящих через точку с координатами lg( —1)=0 и lg(L/G) =1,95. Угол наклона прямой к оси абсцисс определяется значением постоянной v . Аналогичный результат дает сопоставление расчетных данных по уравнению (7.20) и данных испытаний круглых и плоских гладких образцов различных размеров при изгибе и растяжении — сжатии, круглых образцов (гладких и с надрезом) различного диаметра при изгибе с вращением и растяжении — сжатии, пластин с отверстием различных размеров при растяжении— сжатии (все образцы были изготовлены из среднеуглеродистой стали одной плавки). Несмотря на такое разнообразие типов и размеров образцов и видов нагружения, все экспериментальные точки достаточно хорошо ложатся на одну прямую. Таким образом, пределы выносливости указанных образцов, найденные
[c.145]
| Рис. 9.54. Напряжения в пластине с отверстием а) при равномерном растяжении в двух направлениях 6) при чистом сдвиге. | 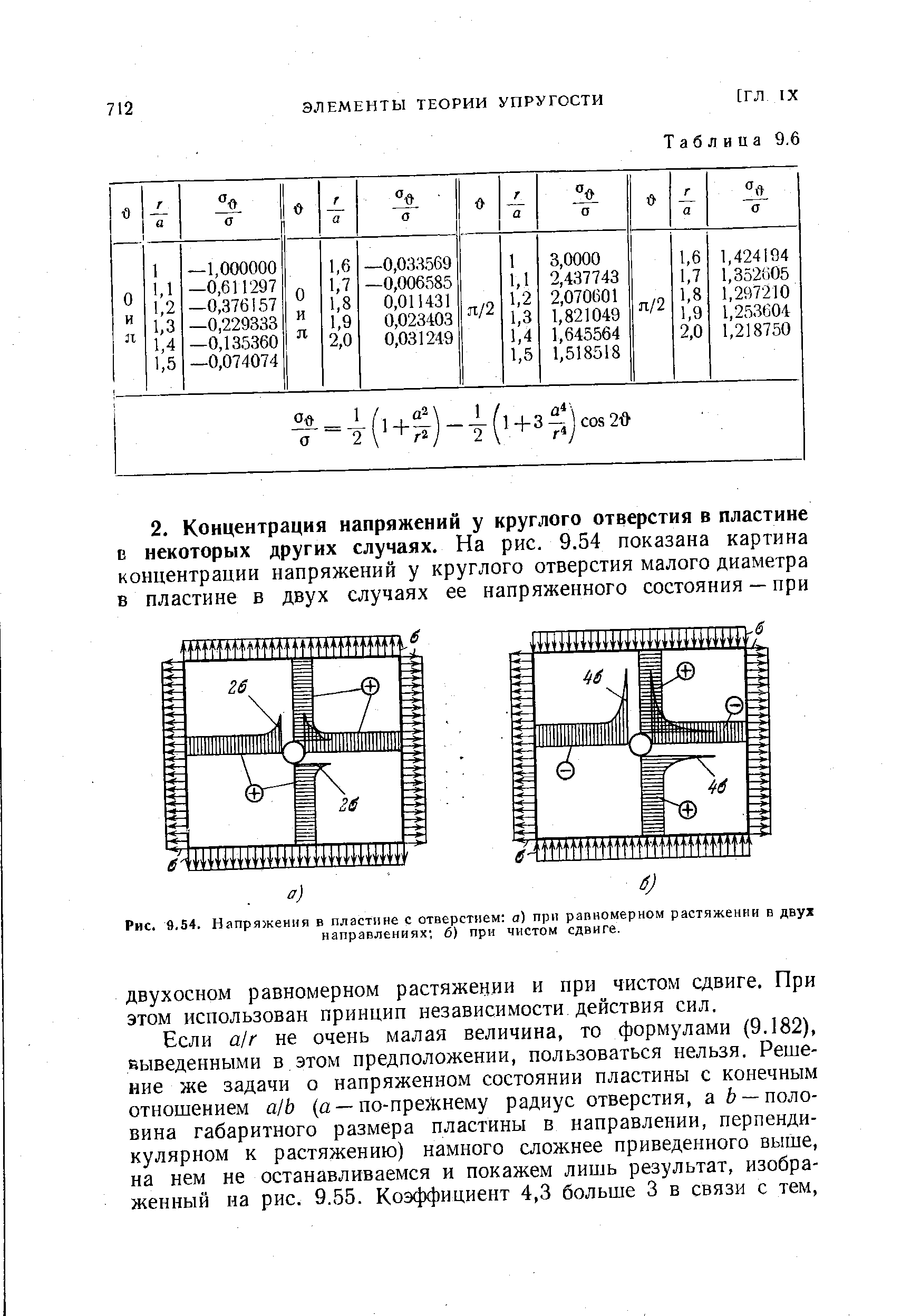 |
В целях определения временных эффектов малоциклового деформирования ([20] изучали кинетику напряженно-деформированного состояния при растяжении-сжатии типичных конструктивных элементов пластины с отверстием при растяжении-сжатии по контуру, цилиндрического стержня с кольцевой выточкой и сильфонно-го компенсатора при заданных осевых перемещениях. Первые два конструктивных элемента, нагруженные заданными максимальными усилиями, имитировали напряженно-деформированное состояние зон концентрации напряжений сосудов давления, работающих при повторных нагрулвнутренним давлением. У сильфонных компенсаторов отсутствуют зоны концентрации напряжений места возникновения максимальных напряжений определяются изгибом гофр, причем повторное нагружение происходит в условиях заданных осевых перемещений. Принятые конструктивные элементы являются характерными и контрастными по условиям нагружения.
[c.202]
Пластины с отверстием и циклический стержень с кольцевой выточкой подвергали растяжению-сжатию при симметричном цикле номинальные напряжения достигали 80… 100 МПа.
[c.204]
В работе [68] выполнен анализ долговечности в зонах концентрации напряжений, В целях определения влияния ползучести на число циклов до разрушения (появления трещины) рассчитали долговечность при циклическом осевом растяжении плоских образцов (пластина с отверстием при повторном осевом растяжении) жаропрочных алюминиевых сплавов. Температуры испытания 120.,, 190° С являются для рассматриваемых материалов достаточно высокими ползучесть и релаксация напряжений выражены.
[c.209]
Растяжение пластины с трещиной, выходящей из кругового отверстия
[c.230]
Сопоставление экспериментального решения в напряжениях задач о растяжении полос с отверстиями и вырезами [1], а также пластины с отверстием и задачи о чистом изгибе прямого бруса [2]
[c.125]
Пример 2. Определить среднее значение И коэффициент вариации предела выносливости пластины с отверстием при растяжении-сжатии (рис. 20) И = 100 мм а = = 10= = мм t = мм.
[c.278]
В случае одноосного растяжения пластины с круговым отверстием и двумя равными щелями в направлении, перпендикулярном линии щелей (см. рис. П27), А. А. Каминский нашел простую приближенную формулу Р ]
[c.539]
Перепад порового давления в анизотропном грунте 269—271 Пластинка с краевым надрезом ( компактный образец ) 231—233 Пластины с отверстием при растяжении 356—358 Пластический куб внутри упругого полупространства 360—361 Пластических деформаций зависимость от времени 338 Поровое давление 282 Потенциал скорости 373 Пошаговые алгоритмы в вязкопластично сти 349—351
[c.487]
При растяжении пластинки с двумя симметричными выточками, как и при растяжении пластин с отверстием, наблюдается смещение максимума осевых растягивающих напряжений от дна выточки в тело пластины, уменьшение Оа и увеличение (в сравнении с упругими значениями) по 1мере развития упругопластических деформаций.
[c.136]
При последовательном растяжении пластины с отверстием различными усилиями PJPy = 2,0) по осям ож и оу картина распределения напряжений несколько меняется. Нагружение пластины усилием Рх = 40 кгс/мм приводит к возникновению в ней большой зоны пластичности (заштрихована на рис. 3.11, а) глубиной порядка 3,2 мм. Последующее растяжение по оси оу Ру = = 20 кгс/мм ) резко уменьшает эту зону, концентрируя ее возле точек Сх — (заштрихована па рис. 3.11, б) с глубиной проникновения около 0,3 мм.
[c.91]
Влияние концентрации напряжений. Концентрация напряжений оказывает существенное влияние на прочность стеклопластиков, так как они не обладают пластическими свойствами. В то же время из-за гетерогенности структуры материала области с концентратором могут исключаться из работы вследствие отслоения, что наблюдалось в материале АГ-4-С. В табл. 127 представлен эффективный коэффициент концентрации при растяжении пластины с отверстием. Испытывались образцы размером 250Х ЮХ 6 мм, вырезанные из плит, при скорости деформирования 1 %/мин.
[c.124]
Растяжение пластины с круглым отверстием (задача Кирша). Пусть радиус отверстия а в несколько раз меньше ширины пластины. Тогда можно считать, что имеем бесконечную пластину, растянутую напряжением = о и имеющую отверстие радиуса а (рис. 4.58). Выделим из пластины кольцо достаточно большого радиуса г = Ъ. Вдали от отверстия имеется простое растяжение Од. = о, поэтому по формулам (4.106) для наклонных нлош адок найдем напряжения
[c.121]
ОДНОСТОРОННЕЕ РАСТЯЖЕНИЕ ПЛАСТИНЫ С МАЛЫМ КРУГОВЫМ ОТВЕРСТИЕМ (ЗАДАЧА КИРША)
[c.302]
Рассматриваемые тела с трещинами условно представим в виде пластины единичной толщины, в которой имеется сквозная прямолинейная щ( ль длиной 21, малой в сравнении с размерами пластины. При этом 21 >> 10 нм. По толщине пластины напряженное и деформированное состояния условно считаем постоянными. Исходя из точного решения задачи теории упругости о растяжении пластины с эллиптическим отверстием, когда равномерное растяжение интенсивностью перпендикулярно направлению большой полуоси эллипса длиной I при стремлении малой полусх и эллипса длиной Ь к нулю, в 1920 г. Гриффитс получил формулу
[c.185]
Растяжение пластины с круговым отверстием (задача Кирша)
[c.398]
Напряжения и деформации в зоне концентрации при осевом растяжении-сжатии цилиндрического стержня с кольцевой выточкой (теоретический коэффициент концентрации напряжений аа = 4,25) рассчитывали с помощью метода конечных элементов. Задача о пластине с отверстием (ао = 2), нагруженной на виешнем контуре
[c.203]
Значения обычно весьма близки ка, т = 6ч-10, так что вторым слагаемым в скобках можно пренебречь, в результате чего последнее выражение приводится к формуле (3.30) при L = = 2яа = nd, где d — диаметр бруса по дну надреза. Все сказанное справедливо и для круглого ступенчатого бруса с переходом от одного сечения к другому по галтели при растяжении-сжатии или изгибе с вращением, причем в этом случае также справедливо уравнение (3.30) при L = nd, Таким образом, уравнение (3.30) применимо для всех деталей, показанных на рис. 3.9 и им аналогичным. Значения параметра L указаны на этом рисунке. Параметр L равен периметру рабочего сечения, если максимальные напряжения одинаковы по всему периметру (круглые брусья при растяжении-слрастяжении-сжатии и круглый ступенчатый брус при изгибе с вращением), но имеющие одно и то же значение критерия подобия -к-, то согласно уравнению (3.30) эти
[c.65]
Окончательно заключаем, что в случае равномерного растяжения пластины с круговым отверстием на бесконечности имеет место единственное условие эквивалентности подкрепления (16.28) впервые установленное Е. Мэнсфилдом [261].
[c.597]
Для надрезанных дисков Винн и Вундт (1958 г.) вывели уравнение, основываясь на исследованиях Бови (1956 г.), которые он выполнил для бесконечной пластины с отверстием, подверженной двухосному растяжению. В отверстии были расходящиеся в стороны трещины. Для диска с двумя диаметрально противоположными надрезами в зоне центрального отверстия это уравнение имеет вид
[c.111]
Основы теории пластичности
(1956) — [
c.230
]
Источник
