Напряжение на растяжение трубы

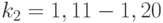
Трубопровод, уложенный в грунт, находится под воздействием внешних сил. Эти силы вызывают сложные напряжения в теле трубы и стыковых соединениях.

В результате действия внутреннего давления в теле трубы возникают следующие главные нормальные напряжения; продольные, кольцевое, радиальное. (см. рис. 1).

2.1. Определяется радиальное напряжение, обусловленное внутренним давлением, равное ему по величине и противоположное по направлению

Рис.1. Напряжение в теле трубы

2.2. Определяется по формуле Мариотта кольцевое напряжение, возникающее в трубе под действием внутреннего и внешнего давлений.

Где d – внутренний диаметр трубы, м

= 240,0

2.3. Определяется продольное напряжение, возникающее от внутреннего давления

где μ – коэффициент Пуассона (коэффициент поперечного сужения при продольном растяжении). Для стали μ = 0,3

= 72,0 МПа

2.4. Определяется по формуле Гука продольное напряжение, возникающее вследствие изменения температуры трубопровода

Где α – коэффициент линейного расширения металла, град-1. Для стали α = 000012 град-1 =

E – модуль упругости стали при растяжении, сжатии и изгибе трубы (модуль Юнга), МПа.

T1 – наименьшая температура грунта на глубине укладки трубы, К;

T1 = +279 К.

T2 – температура воздуха во время укладки трубопровода в траншею, К;

T2 = +288 К.

2.5. Определяются продольные напряжения, появляющиеся в трубе при ее холодном упругом изгибе, который является следствием неровностей рельефа

Где ρи — радиус изгиба трубы, м. В соответствии со СНиП III – 42-80* радиус изгиба трубы равен не менее 1000 Dy – условный диаметр трубопровода. У проектируемого газопровода ρи = 1000 м.

Проверка прочности трубопровода при эксплуатации

При эксплуатации трубопровода совместное действие внутреннего давления и изгибающих условий может вызвать гораздо большие суммарные напряжения в продольном направлении трубы, чем в момент испытаний. Уязвимым местом трубопровода в этом случае могут оказаться поперечные сварные швы. Прочность поперечных сварных швов в наиболее тяжелый период эксплуатации проверяют из условия, что суммарная продольная нагрузка должна быть меньше расчетного сопротивления трубы (так называемой несущей способности трубы).

Где np, nt, npи – коэффициенты перегрузки, которые при учете совместного действия могут быть приняты равными единице.

Тогда

Вывод:

Прочность трубопровода при эксплуатации обеспечена.

Таблица вариантов

Вариант
Диаметр трубопровода D, м	0,377	0,82	0,53	1,02	0,63	0,72	0,72	0,53	0,426	0,63
p, МПа	5,5	7,6	5,8	5,6	5,2	5,6	6,0	5,6	5,5	7,6
t1	4,5	3,5
t2	15,5
pи, м
Категория участка	I	II	III	IV	I	II	III	IV	I	II

Вариант
Диаметр трубопровода D, м	1,02	0,426	0,63	1,22	1,22	1,42	0,53	1,22	0,426	0,325
p, МПа	5,8	5,6	5,0	7,6	5,4	7,6	5,2	7,6	5,4	5,6
t1	3,8	4,2
t2	11,5
pи, м
Категория участка	III	IV	I	II	III	IV	I	II	III	IV

Вариант
Диаметр трубопровода D, м	0,82	0,377	1,22	0,72	0,377	1,22	0,63	0,82	1,22	1,42
p, МПа	5,5	7,6	5,2	7,6	5,4	5,6	4,8	5,6	5,0	7,6
t1
t2
t2
Категория участка	I	II	III	IV	I	II	III	IV	I	II

Напряжения в трубопроводах и толщина стенок труб

К нагрузкам трубопровода относят внутреннее давление продукта в трубе, вес конструкций, давление грунта, снега и ветра, внешнее гидростатическое давление и архимедова сила. К воздействиям относят предварительное напряжение элементов, изменение температуры, просадки оснований и сейсмические явления. Учет внутреннего давления при расчетах прочности трубопроводов обязателен, а остальные нагрузки учитываются в зависимости от конкретных условий.

Нормативные нагрузки — это наибольшие внешние нагрузки, допускаемые при нормальной эксплуатации трубопровода. Расчетные нагрузки отличаются от нормативных нагрузок на величину коэффициента надежности по перегрузке п при наиболее неблагоприятных сочетаниях.

Нагрузки и воздействия, связанные с осадками и пучениями грунта, перемещением опор определяются на основании анализа грунтовых условий в процессе строительства и эксплуатации трубопровода. Параметры сейсмических колебаний грунта назначаются без учета заглубления трубопровода, а как для сооружения, расположенного на поверхности земли.

Нормативный температурный перепад в металле стенок труб принимается равным разнице между максимальной или минимальной температурой стенок в процессе эксплуатации и наименьшей или наибольшей температурой, при которой фиксируется расчетная схема трубопровода (привариваются компенсаторы, проводится засыпка трубы), т. е. когда фиксируется статически неопределимая система.

При установлении температурного перепада и невозможности температурных деформаций в трубопроводе сформируются следующие напряжения:

(
8.10)

где — коэффициент линейного расширения материала трубы; — модуль упругости материала трубы; — температура, при которой фиксируются элементы конструкции в проектном положении; — наибольшая или наименьшая расчетная температура.

Усилия в трубопроводе, действующие в тангенциальном направлении, называют кольцевыми (
рис.
8.3), в осевом направлении — продольными.

Схема внутренних напряжений в трубе

Рис.
8.3.
Схема внутренних напряжений в трубе

Под воздействием внутреннего давления в трубе с внутренним диаметром в стенке толщиной формируется кольцевое напряжение

(
8.11)

Зависимость между продольными и поперечными (кольцевыми) напряжениями определяется через коэффициент Пуассона m следующим образом:

(
8.12)

В процессе строительства трубопровод искривляется как в горизонтальном, так и в вертикальном направлении. Изгиб вызывает появление в стенке трубы дополнительных напряжений, которые зависят от радиуса упругого изгиба и геометрических характеристик трубы.

Если трубопровод не может перемещаться в продольном и поперечном направлении, то при совместном действии внутреннего давления, температуры и изгибающего момента продольные напряжения в искривленном трубопроводе определяются следующей зависимостью:

(
8.13)

Здесь — кольцевые напряжения от рабочего нормативного давления; — внутренний диаметр трубы; — номинальная толщина стенки трубы; — коэффициент Пуассона материала трубы; — коэффициент линейного расширения металла трубы; — расчетный температурный перепад (положительный при нагревании); — модуль упругости (модуль Юнга) материала трубы; — минимальный радиус упругого изгиба оси трубопровода; — наружный диаметр трубопровода.

Знак «минус» в (8.13) относится к случаю, когда имеет отрицательное значение, т. е. расчетная температура меньше начальной температуры. В таком случае растягивающие продольные напряжения увеличиваются. В случае, когда имеет положительное значение, растягивающие напряжения уменьшаются и даже могут стать сжимающими.

Под прочностью трубопровода понимают его способность сопротивляться внутренним и внешним нагрузкам без разрушения и без потери устойчивости. Для обеспечения прочноети необходимо определить напряжения в стенках трубопровода от различных нагрузок и сравнить с контролируемым сопротивлением материала трубы . Если расчетные напряжения окажутся меньше значения , прочность считается обеспеченной.

Сопротивление материала нагрузкам характеризуется диаграммой растяжения или сжатия. На этой диаграмме имеются обычно три характерных значения: — напряжения на конце участка упругой зависимости: — напряжения на площадке текучести; — временное сопротивление разрыву, при котором происходит быстрое разрушение материала. Например, для стали Ст.3 , а . Принимая в расчетах в качестве контролируемого сопротивления , получим одно значение толщины стенки труб, а принимая — другое значение толщины стенок.

Магистральные трубопроводы рассчитываются на нагрузки и воздействия по методу предельных состояний. Для всех схем их прокладки принимают два предельных состояния работы материала:

Напряжения в материале трубы определяют от всех нормативных нагрузок и воздействий с учетом продольных и поперечных перемещений трубопровода в соответствии с правилами строительной механики и курса сопротивления материалов.

В строительных нормах в качестве расчетных сопротивлений приняты два контролируемых сопротивления растяжению (сжатию) и , которые следует определять по формулам:

(
8.14)

(
8.15)

Здесь — коэффициент условий работы трубопровода, зависящий от категории трубопровода и его участка; и — коэффициенты надежности (безопасности) по материалу труб с учетом технологии их изготовления и сварки; — коэффициент надежности, учитывающий внутреннее давление, диаметр и назначение трубопровода.

В последних зависимостях значение принимается равным минимальному значению для материала; принимается равным пределу текучести по техническим условиям на трубы.

В соответствии с методикой расчета прочности по предельным состояниям различают расчетные и нормативные нагрузки. Расчетные нагрузки учитывают их возможное отклонение от нормативных с помощью различных значений коэоффици-ентов перегрузки.

Расчетная толщина стенки трубопровода определяется следующей зависимостью:

(
8.16)

Здесь — коэффициент перегрузки или коэффициент надежности по рабочему давлению в трубопроводе: — рабочее нормативное давление: — наружный диаметр трубопровода.

Пусть трубопровод с наружным диаметром 1220 мм работает при рабочем давлении . Нормативное расчетное сопротивление материала стенки трубы . Коэффициент безопасности по материалу , коэффициент надежности , коэффициент перегрузки , коэффициент условий работы . При таких условиях работы толщина стенок трубопровода должна быть равной .

При наличии в трубопроводе продольных осевых сжимающих напряжений расчетная толщина стенки трубопровода определяется по формуле (8.16), в которой расчетное сопротивление умножается на коэффициент . учитывающий двухосное напряженное состояние трубы:

(
8.17)

где — абсолютное значение продольных сжимающих напряжений от расчетных нагрузок и воздействий.

Толщину стенки труб следует принимать не менее , но не менее 4 мм для труб диаметром свыше 200 мм. Полученное расчетное значение толщины стенки трубы округляется до ближайшего большего значения, предусмотренного ГОСТом.

Источник

ПОДВЕРЖЕННОЙ ДЕЙСТВИЮ ВНУТРЕННЕГО ДАВЛЕНИЯ, ПРОДОЛЬНОЙ СИЛЫ И КРУТЯЩЕГО МОМЕНТА

(ЗАДАЧА № 9)

Основные формулы

Рис. 2.21. Тонкостенная труба под действием внутреннего
давления, продольной силы и крутящего момента

Рассматривается длинная прямолинейная цилиндрическая тонкостенная труба (рис. 2.21) с , . Труба нагружена внутренним давлением , по ее торцам приложены силы и крутящие моменты .

Напряжения в трубе обозначаем, используя местную декартову систему координат x, y, z: ось x параллельна оси трубы, ось z направлена по касательной к срединной линии поперечного сечения, осью y служит продолжение радиуса R.

Сила вызывает в поперечном сечении трубы продольное усилие и создает нормальное напряжение (рис. 2.22)

Рис. 2.22. Напряжения
в трубе от продольной силы

Рис. 2.23. Напряжения в трубе от
внутреннего давления

Здесь – площадь поперечного сечения тонкостенной трубы.

Внутреннее давление вызывает растяжение трубы в кольцевом направлении (рис. 2.23), чему соответствует напряжение в продольных сечениях трубы:

Рис. 2.24. Напряжения
в трубе от крутящего
момента

Напряжения положительны при . Случай отвечает давлению, приложенному к наружной поверхности.

Крутящий момент создает касательные напряжения (рис. 2.24):

Они направлены так, чтобы уравновесить пару сил М.

По толщине трубы напряжения распределены равномерно. Остальные напряжения либо в точности равны нулю, либо малы: , .

Напряженное состояние элементарного параллелепипеда, вырезанного из трубы (рис. 2.25), является плоским. Анализ напряженного состояния выполняется так же, как в задаче № 7.

Условие задачи

Рис. 2.25. Напряженное
состояние точки трубы

Труба с радиусом сечения м толщиной см загружена продольной растягивающей силой кН, внутренним давлением МПа и крутящим моментом . Материал трубы – чугун с такими характеристиками: МПа, МПа, . Нормативный коэффициент запаса прочности .

Требуется:

1) найти напряжения на гранях элемента, выделенного из трубы;

2) найти главные напряжения и положения главных площадок;

3) проверить прочность и определить действительный коэффициент запаса прочности;

4) показать направление трещины, возникающей при повышении уровня напряженного состояния до критического.

В расчетно-графической работе студенту требуется, кроме того, вычислить напряжения по указанной наклонной площадке. Это задание выполняется так же, как в задаче № 7.

Решение

Начать решение задачи нужно с изображения трубы и действующих на нее сил. Рядом со стрелками указываются абсолютные значения сил. Знаки учитываются соответствующим направлением стрелок.

Проверим применимость к данной задаче формул для вычисления напряжений в тонкостенной трубе. Так как , то труба является тонкостенной. Следовательно, вышеприведенные формулы применимы.

Нормальное напряжение от продольного растяжения силой

положительно.

Нормальное напряжение, вызванное внутренним давлением ,

МПа

также положительно.

Касательное напряжение, вызванное моментом , по модулю равно

Принимая во внимание направление крутящего момента (см. рис. 2.24) и учитывая правило знаков для касательного напряжения при плоском напряженном состоянии, получаем .

Теперь изобразим найденное напряженное состояние точки трубы в виде плоского рисунка, учтя правила знаков для напряжений. Для последующей проверки прочности вычислим главные напряжения:

Главные напряжения, пронумерованные должным образом,

, , .

Тангенс угла наклона главной площадки

Отсюда два главных угла

Соответствие угла главным площадкам (1 или 2) устанавливается так же, как в задаче № 7. Главные направления 1 и 2 показаны на рис. 2.26. Проверку вычисленных значений главных напряжений и главных направлений можно выполнить графически, построив круг напряжений Мора. Построение круга напряжений описано при решении задачи № 7.

Материал является хрупким (чугун), поэтому с целью проверки прочности используем вторую теорию прочности или теорию прочности Мора.

Согласно второй теории прочности

значит, прочность обеспечена.

Вычислим действительный коэффициент запаса прочности:

Рис. 2.26. Вероятное
направление трещин

Вероятная плоскость отрыва (трещины) перпендикулярна первому главному направлению, то есть наклонена к продольной оси трубы под углом . Она показана на рис. 2.26, где ось – продольная ось трубы. Направление вероятной плоскости отрыва на рисунке привязано к оси конструкции, значит, может быть показано и на самой конструкции.

Согласно пятой теории прочности (теории Мора)

то есть прочность также обеспечена. Вычислим фактический коэффициент запаса прочности:

КРУЧЕНИЕ

Рекомендуемая литература

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл.5 (§ 5.1–5.4), гл. 11 (§ 11.5);

Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 6 (§ 27, 29–30, 32);

Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 6 (§ 6.1–6.4, 6.6, 6.7).

Основные понятия и формулы

При кручении поперечные сечения стержня поворачиваются вокруг его продольной оси, а продольные волокна при этом искривляются, превращаясь в пространственные кривые. Кручение вызывается парами сил, действующими в плоскости поперечных сечений. В поперечных сечениях стержня возникает одно внутреннее усилие — крутящий момент Мк. Стержень, работающий на кручение, принято называть валом.

Рис. 3.1. Правило знаков для крутящего
момента

Крутящие моменты в сечениях определяются, как и другие виды усилий, методом сечений. Крутящий момент в сечении равен сумме моментов внешних сил, действующих по одну сторону от сечения, относительно продольной оси стержня. Примем правило знаков для крутящего момента: его положительное направление соответствует повороту сечения по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали (рис. 3.1).

Напряженное состояние в любой точке поперечного сечения при кручении является чистым сдвигом, и в точках поперечного сечения возникают касательные напряжения.

Касательные напряжения при кручении стержня круглого сечения с радиусом R (или кольцевого сечения с внешним радиусом R) определяются по формуле

, (3.1)

Рис. 3.2. Распределение
касательных напряжений
в круглом сечении

где — расстояние от центра до точки, в которой мы определяем t. Эти напряжения направлены перпендикулярно радиусу, соединяющему центр круга с рассматриваемой точкой. Эпюра распределения касательных напряжений на любом диаметре будет иметь вид, показанный на рис. 3.2. Максимальные касательные напряжения, как следует из формулы (3.1), действуют в точках на контуре сечения и они равны

, (3.2)

где – полярный момент сопротивления.

Деформацию стержня круглого (кольцевого) сечения при кручении характеризует угол закручивания поперечного сечения на участке длиной (рис. 3.3)

. (3.3)

Относительная величина этого угла (на единицу длины) называется погонным углом закручивания

. (3.4)

Рис. 3.3. Деформация стержня при кручении

Эпюры распределения касательных напряжений в стержнях прямоугольного сечения показаны на рис. 3.4. Максимальные касательные напряжения действуют в точках, расположенных по середине длинной стороны сечения. Они равны

. (3.5)

Напряжения в точках по середине короткой стороны

Рис. 3.4. Распределение
касательных напряжений
в прямоугольном сечении

. (3.6)

Погонный и полный углы закручивания для стержней прямоугольного сечения определяются по формулам

; . (3.7)

Геометрические характеристики сечения, входящие в формулы (3.1)–(3.7), можно найти следующим образом:

Полярный момент инерции и полярный момент сопротивления:

* для круглого сечения

, ; (3.8)

* для кольцевого сечения

; . (3.9)

Здесь — отношение радиусов внутреннего и внешнего контуров кольца.

Для стержня прямоугольного сечения геометрическая характеристика жесткости

(3.10)

и момент сопротивления кручению

, (3.11)

где — меньшая сторона прямоугольного сечения, а коэффициенты , , в формулах (3.6), (3.10), (3.11) определяются в зависимости от отношения сторон сечения по таблицам, имеющимся в справочной литературе, например в [3, § 6.6].

Модуль сдвига в формулах (3.3) и (3.7)

. (3.12)

Целью расчета вала на кручение, как правило, является удовлетворение двум условиям: прочности и жесткости. Условие прочности в опасной точке вала при кручении записывается так:

, (3.13)

где [t] берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:

* из второй теории прочности

; (3.14)

* из теории Мора

, (3.15)

где .

Из теорий прочности для пластичных материалов при чистом сдвиге получим:

* по третьей теории прочности

, (3.16)

* по четвертой теории прочности

. (3.17)

Условие жесткости вала при кручении – это условие, ограничивающее деформации стержня, а именно:

, (3.18)

где – допускаемый погонный угол закручивания, величина которого нормируется.

Удовлетворяя этим двум условиям, можно либо подбирать размеры сечения, либо определять допускаемую нагрузку на стержень.

Источник