На рисунке представлена диаграмма растяжения материала закон гука
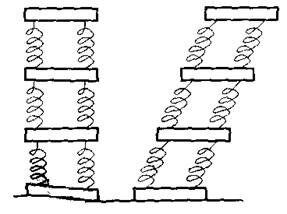
Диаграммы нагружения и разгружения образцов.
Закон повторного нагружения
        Диаграмма растяжения образца позволяет оценить поведение материала образца в упругой и упруго-пластической стадиях деформирования, определить механические характеристики материала.
        Для получения численно сопоставимых между собой механических характеристик материалов диаграммы растяжения образцов перестраивают в диаграммы растяжения материалов, т.е. в зависимость между напряжением   и деформацией  , которые определяют по формулам
     ,
где - сила, действующая на образец,
     
 - начальная площадь поперечного сечения и начальная длина расчетной части образца.
        Диаграмма растяжения материала, полученная при этих условиях (без учета изменения размеров расчетной части образца), называется условной диаграммой растяжения материала в отличие от действительной диаграммы растяжения, которую получают с учетом изменений размеров образца.
        Диаграмма растяжения материала зависит от его структуры, условий испытаний (температуры, скорости деформирования).
   
        Диаграмма растяжения образца из низкоуглеродистой стали при однократном нагружении до разрушения. Конечная точка диаграммы соответствует разрушению.
        На начальном участке диаграммы между силой   и удлинением   соблюдается прямая пропорциональная зависимость — образец подчиняется
закону Гука. В точке А диаграммы закон Гука нарушается: зависимость между силой и удлинением становится нелинейной. На диаграмме наблюдается горизонтальный участок (участок БВ), называемый площадкой текучести. В этой стадии испытания образец удлиняется (деформируется) практически при постоянной силе. Это явление называется текучестью, при этом образец деформируется равномерно и по всей длине рабочей части. В точке В площадка текучести заканчивается и начинается участок упрочнения. В конечной точке Д этого участка достигается максимальная сила, которую может выдержать образец.
        При нагружении до предела пропорциональности (точка Г диаграммы) и при дальнешем уменьшении нагрузки образец разгружается по линейному закону, который совпадает с законом первичного нагружения. В этом заключается «закон разгрузки». При нагружении образца в пределах действия закона Гука законы нагружения и последующего разгружения совпадают. При полной разгрузке образца его размеры и форма возвращаются к первоначальной кривой однократного нагружения.
        Напряженное состояние образца до точки Д — одноосное.
        Далее начинается участок разрушения или участок местной текучести. Он характеризуется местным утонением образца и появлянием шейки.
        На конечном участке ДЕ (после возникновения шейки) происходит локализация деформаций в шейке, в остальной части образца они практически не увеличиваются. Деформация в шейке неоднородная, имеет существенный градиент вдоль оси образца. Напряженное состояние на этом участке становится неоднородным, кроме того, оно изменяется качественно — становится трехосным.
Диаметр шейки уменьшается по мере деформирования образца, и образец разрывается по наименьшему сечению шейки.
        Если при испытании на растяжение нагружение приостановить, например, в точке Г диаграммы и осуществить разгружение образца, то окажется, что диаграмма разгружения и диаграмма предыдущего нагружения не совпадают. Линия разгружения в этом случае — прямая, параллельная начальному линейному участку диаграммы растяжения образца. Такой характер деформирования образца при его разгружении называется законом разгружения.
При повторном нагружении диаграмма до точки Г совпадает с линией разгружения, а затем будет совпадать с диаграммой растяжения образца при однократном нагружении.
Такой характер деформирования называется законом повторного нагружения и заключается в пропорциональной зависимости силы и удлинения, которая сохраняется до значения силы, достигнутой при первичном нагружении.
         При разгружении образца в пределах участка ОА законы нагружения, разгружения и повторного нагружения совпадают.
Источник
Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.
Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).
Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.
Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
На рис. 1 показана диаграмма для малоуглеродистой стали. Она построена в системе координат F-Δl, где:
F — продольная растягивающая сила, [Н];
Δl — абсолютное удлинение рабочей части образца, [мм]

Рис. 1 Диаграмма растяжения стального образца
Как видно из рисунка, диаграмма имеет четыре характерных участка:
I — участок пропорциональности;
II — участок текучести;
III — участок самоупрочнения;
IV — участок разрушения.
Построение диаграммы
Рассмотрим подробнее процесс построения диаграммы.
В самом начале испытания на растяжение, растягивающая сила F, а следовательно, и деформация Δl стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О).
На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня Δl растут пропорционально увеличивающейся нагрузке F.
После прохождения точки А диаграмма резко меняет свое направление и на участке II начинающемся в точке B линия какое-то время идет практически параллельно оси Δl, то есть деформации стержня увеличиваются при практически одном и том же значении нагрузки.
В этот момент в металле образца начинают происходить необратимые изменения. Перестраивается кристаллическая решетка металла. При этом наблюдается эффект его самоупрочнения.
После повышения прочности материала образца, диаграмма снова «идет вверх» (участок III) и в точке D растягивающее усилие достигает максимального значения. В этот момент в рабочей части испытуемого образца появляется локальное утоньшение (рис. 2), так называемая «шейка», вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).
Рис. 2 Стальной образец с «шейкой»
Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения образца, растягиваещее усилие необходимое для его растяжения уменьшается, и кривая диаграммы «идет вниз».
В точке E происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована «шейка»
Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:
W=0,8Fmax∙Δlmax
По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.
Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.
Предел пропорциональности >
Примеры решения задач >
Лабораторные работы >
Источник
Графическое изображение зависимости между напряжениями (или нагрузками) и деформациями материала (или перемещениями при деформировании) представляет собой диаграмму деформирования.
Испытательные машины имеют специальные приспособления, которые автоматически фиксируют диаграмму растяжения. На диаграмме по оси ординат откладываются действующие осевые нагрузки, а по оси абсцисс — абсолютные деформации.
На рис. 2.2 даны типичные диаграммы растяжения различных металлов. Диаграмма с постепенным переходом из упругой в пластическую область (рис. 2.2, а) свойственна большинству металлов в пластичном состоянии (легированные стали, медь, бронза).
Рис. 2.2. Диаграммы растяжения:
а — для большинства металлов в пластичном состоянии с постепенным переходом из упругой в пластическую область; б — для некоторых металлов в пластичном состоянии со скачкообразным переходом в пластическую область; в — для хрупких металлов
Пластичные материалы разрушаются при больших остаточных деформациях (больших остаточных удлинениях, измеряемых после разрыва).
Диаграмма со скачкообразным переходом в пластическую область в виде четко обозначенной «площадки» текучести (рис. 2.2, б) свойственна некоторым металлам. К таким металлам можно отнести мягкую углеродистую сталь, а также некоторые отожженные марганцовистые и алюминиевые бронзы.
Хрупкие материалы разрушаются при малых остаточных деформациях. К хрупким материалам можно отнести закаленную и неотпущенную сталь, серый чугун.
Характерные участки и точки диаграммы растяжения показаны на рис. 2.3. По оси абсцисс откладывают абсолютные удлинения А/ образца, а по оси ординат — значения растягивающей силы Р. Сначала получим на первом участке диаграммы 0—1 прямолинейную зависимость между силой и удлинением, что отражает закон Гука. При дальнейшем увеличении силы (за точкой 1) прямолинейная зависимость между Р и А/ нарушается. Точка 1 соответствует пределу пропорциональности, т. е. наибольшему напряжению, при котором еще соблюдается закон Гука. Если нагрузку, соответствующую точке 1, обозначить ,Pnu, а начальную площадь сечения образца Fq, то предел пропорциональности
Рис. 2.3. Характерные участки и точки диаграммы растяжения
Несколько выше точки 1 находится точка Г, соответствующая пределу упругости. Если нагрузку, соответствующую точке Г, обозначить через Руп, то предел упругости
По ГОСТу предел упругости задается и обозначается ag os — напряжение, при котором остаточное удлинение достигает 0,05 % длины участка образца, равного базе тензометра.
За точкой Г возникают уже заметные остаточные деформации. В точке 2 диаграммы частицы материала начинают переходить и область пластичности — наступает явление текучести образца.
На диаграмме растяжения получается горизонтальный участок 2—3 (площадка текучести), параллельный оси абсцисс. Для участка 2—3 характерен рост деформации без заметного увеличения нагрузки. Обозначим величину нагрузки, соответствующей площадке текучести 2—3, через Рт. Напряжение ат, отвечающее этой нагрузке, это то напряжение, при котором рост деформации происходит без заметного увеличения нагрузки, оно и является физическим пределом текучести.
Предел текучести (физический) — это механическая характеристика материалов: напряжение, отвечающее нижнему положению площадки текучести в диаграмме растяжения для материалов, имеющих эту площадку (см. рис. 2.3):
Предел текучести устанавливает границу между упругой и упруго-пластической зонами деформирования.
Даже небольшое увеличение напряжения (нагрузки) выше предела текучести вызывает значительные деформации.
Для материалов, не имеющих на диаграмме площадки текучести, принимают условный предел текучести: напряжение, при котором остаточная деформация образца достигает определенного значения, установленного техническими условиями (большего, чем это установлено для предела упругости).
Обычно допуском для величины остаточной деформации при растяжении принято остаточное удлинение 0,2 %. Эта величина называется условным пределом текучести:
где Pq 2 — нагрузка при условном пределе текучести.
При увеличении напряжений сверх предела текучести при растяжении в результате сильной деформации происходит упрочнение металла (изменение его структуры и свойств) и сопротивление деформации увеличивается, поэтому за участком текучести, т. е. за точкой 3, наблюдается подъем кривой растяжения (участок упрочнения). До точки 4 удлинение образца происходит равномерно. Наибольшее значение нагрузки, предшествовавшее разрушению образца, обозначим Рмакс. Точка 4 характеризует максимальное условное напряжение, возникающее в процессе испытания, называемое временным сопротивлением.
Временное сопротивление ав — условное напряжение, определяемое по отношению действующей силы к исходной площади поперечного сечения образца и отвечающее наибольшей нагрузке ^макс’ предшествовавшей разрушению образца:
В момент, соответствующий нагрузке Рмакс, появляется заметное местное сужение образца (шейка). Если до этого момента образец имел цилиндрическую форму, то теперь растяжение образца сосредоточивается в области шейки.
Участку 4—5 соответствует быстрое уменьшение сечения шейки, вследствие чего растягивающая сила уменьшается, хотя напряжение растет (площадь сечения в шейке ^врFq).
При дальнейшей деформации шейка сужается и образец разрывается по наименьшему сечению FK, где напряжения в действительности достигают наибольшей величины. Таким образом, нарастание пластической деформации при растяжении происходит поэтапно: равномерная пластическая деформация до точки 4 и местная пластическая деформация от точки 4 до точки 5 — момента разрушения.
Моменту разрыва соответствует точка 5, усилие разрыва обозначим Рк. Отношение разрывающего усилия к действительной площади сечения в месте разрыва называется истинным сопротивлением разрыву:
У пластичных металлов в является характеристикой сопротивления пластической деформации, а у хрупких — характеристикой сопротивления разрушению.
Для пластичных материалов, образующих при растяжении шейку, характеристикой сопротивления разрушению служит истинное сопротивление разрыву (при разрушении).
При определении пределов пропорциональности, упругости, текучести и временного сопротивления соответствующая им нагрузка Р относилась к начальной площади поперечного сечения образца, т. е. площади образца до испытания. При растяжении образца в области упругой деформации или близко от нее, т. е. при определении пределов пропорциональности и упругости, можно пренебречь небольшим изменением площади сечения образца.
Однако в области пластической деформации изменение сечения образца становится значительным. Поэтому теоретически возможно для определения временного сопротивления и предела текучести относить соответствующую нагрузку не к исходной площади образца, а к его действительной площади, которую он имеет в момент приложения соответствующей нагрузки.
Напряжения, определенные по отношению приложенной нагрузки к начальной площади образца, называются условными напряжениями, а определенные по отношению к действительной площади — истинными.
На рис. 2.4 дана диаграмма истинных напряжений. В диаграмме по оси абсцисс откладывается относительное удлинение с = Д///0, а по оси ординат — нормальное напряжение а = P/Fq, где /0 и Fq — первоначальные длина и площадь сечения образца. Диаграмма в координатах «напряжения — деформации» на участке 4—5 является условной, как было указано выше. При напряжении, соответ-
Рис. 2.4. Диаграмма истинных напряжений ствующем временному сопротивлению (точка 4), образуется шейка и площадь сечения резко уменьшается, поэтому истинное напряжение увеличивается и истинная диаграмма 4—5′ расположена выше условной диаграммы 4—5.
Следует отметить, что временное сопротивление не совпадает с сопротивлением разрыву и оказывается меньше последнего. Истинное сопротивление разрыву получается делением наибольшей нагрузки Рпч (точка 4′) на истинную уменьшенную площадь сечения FBp в момент начала появления шейки.
Таким образом, истинные напряжения с увеличением деформации непрерывно растут до момента разрушения образца.
Показателем пластической деформации является его абсолютное остаточное удлинение А/0Ст.п ПРИ разрыве (отрезок ОЛ[ на рис. 2.3), так как упругая деформация (отрезок A^2) исчезает после разрыва:
где /0 — начальная длина образца, /к — конечная длина образца (рис. 2.5).
Общее удлинение образца при растяжении слагается из равномерного и сосредоточенного удлинения (за счет образования шейки). Так как размеры испытуемых образцов могут быть различными, то характеристикой пластичности образца служит не его абсолютное, а относительное остаточное удлинение при разрыве 6 — отношение приращения расчетной длины образца после разрыва
к первоначальной расчетной длине /0 в процентах:
Чем больше 5, тем пластичнее металл.
Рис. 2.5. Образцы до растяжения (а) и после растяжения (б)
Другой характеристикой пластичности металла является относительное сужение сечения ц/ после разрыва (в процентах) — отношение разности начальной площади и минимальной площади поперечного сечения образца разрыва к начальной площади поперечного сечения образца.
Если Fq — начальная площадь образца, FK — минимальная площадь сечения в месте образования шейки (в месте разрыва), то относительное сужение (в процентах)
При оценке свойств образцов пластических материалов большое значение имеет их сопротивление пластической деформации. Оно показывает, какое напряжение можно допустить, не вызывая (или вызывая допускаемую величину) пластической деформации, т. е. изменения металла под действием внешних сил.
Свойства, характеризующие сопротивление пластической деформации, можно разделить на две группы: сопротивление металла малым пластическим деформациям и сопротивление металла значительным пластическим деформациям.
Величиной, характеризующей сопротивление малым пластическим деформациям, является предел упругости. Свойства сопротивления металла значительным пластическим деформациям проявляются при напряжениях выше условного предела текучести. Для пластических металлов временное сопротивление определяет сопротивление их значительным пластическим деформациям. Временное сопротивление является основной характеристикой хрупких материалов, разрушающихся при малых пластических деформациях.
В табл. 2.1 приведены механические характеристики некоторых материалов.
Источник
Деформация
Деформация (от лат. Deformatio – искажение) – изменение формы и размеров тела под действием внешних сил.
Деформации возникают потому, что различные части тела движутся по-разному. Если бы все части тела двигались одинаково, то тело всегда сохраняло бы свою первоначальную форму и размеры, т.е. оставалось бы недеформированным. Рассмотрим несколько примеров.
- Возьмем мягкую резинку для карандаша и нажмем на нее пальцем (рис. 1). Палец, нажимающий на резинку, перемещает верхние слои резинки; нижний слой, лежащий на столе, остается неподвижным, так как он соприкасается с гораздо более жесткой, чем резинка, поверхностью стола. Разные части резинки смещаются по-разному, и резинка меняет свою форму: возникает деформация. Деформированная резинка действует на соприкасающиеся с ней тела с некоторой силой. Палец отчетливо чувствует давление резинки. Если палец убрать, то резинка примет прежнюю форму.
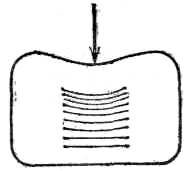
Рис. 1
- Возьмем мягкую цилиндрическую пружину и медленно опустим ее одним концом на стол. Пружина окажется сжатой (рис. 2). Происходит эта деформация следующим образом: после того как нижний виток пружины коснулся поверхности стола, этот виток перестает двигаться, верхние же витки пружины продолжают опускаться и приближаются к нижним виткам; пружина сжимается, и появляются силы упругости; движение верхних витков прекращается только тогда, когда возникшая в результате сжатия сила упругости будет в любом месте пружины действовать на вышележащие витки с силой, равной их весу. Но для этого витки пружины должны быть сжаты тем сильнее, чем ниже они расположены, так как действующая с их стороны сила упругости должна уравновешивать вес большего числа витков.
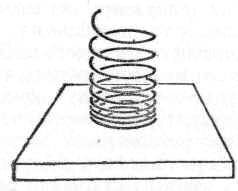
Рис. 2
- Пусть на тело действуют силы упругости. Эти силы не могут сообщать ускорений внутренним частям ускоряемого тела. Значит, ускоряемое тело может начать двигаться как целое только после того, как внутри него возникнут деформации, а вместе с ними и силы упругости, которые сообщат внутренним частям тела требуемое ускорение. Таким образом, тело, движущееся с ускорением под действием сил, возникающих при непосредственном соприкосновении, во всех случаях окажется деформированным. Эти деформации и являются причиной возникновения силы, действующей со стороны ускоряемого тела на соприкасающееся с ним ускоряющее.
Виды деформации
Деформации растяжения и сжатия. Если к однородному, закрепленному с одного конца стержню приложить силу F вдоль его оси в направлении от стержня, то он подвергнется деформации растяжения. Деформацию растяжения испытывают тросы, канаты, цепи в подъемных устройствах, стяжки между вагонами и т.д. Если на закрепленный стержень подействовать силой вдоль его оси по направлению к стержню, то он подвергнется сжатию. Деформацию сжатия испытывают столбы, колонны, стены, фундаменты зданий и т.п. При растяжении или сжатии изменяется площадь поперечного сечения тела.
Деформация сдвига. Деформацию сдвига можно наглядно продемонстрировать на модели твердого тела, представляющего собой ряд параллельных пластин, соединенных между собой пружинами (рис. 3). Горизонтальная сила F сдвигает пластины друг относительно друга без изменения объема тела. У реальных твердых тел при деформации сдвига объем также не изменяется. Деформации сдвига подвержены заклепки и болты, скрепляющие части мостовых ферм, балки в местах опор и др. Сдвиг на большие углы может привести к разрушению тела – срезу. Срез происходит при работе ножниц, долота, зубила, зубьев пилы и т.д.

Рис. 3
Деформация изгиба. Легко согнуть стальную или деревянную линейку руками или с помощью какой-либо другой силы. Балки и стержни, расположенные горизонтально, под действием силы тяжести или нагрузок прогибаются – подвергаются деформации изгиба. Деформацию изгиба можно свести к деформации неравномерного растяжения и сжатия. Действительно, на выпуклой стороне (рис. 4) материал подвергается растяжению, а на вогнутой – сжатию. Причем чем ближе рассматриваемый слой к среднему слою KN, тем растяжение и сжатие становятся меньше. Слой KN, не испытывающий растяжения или сжатия, называется нейтральным. Так как слои АВ и CD подвержены наибольшей информации растяжения и сжатия, то в них возникают наибольшие силы упругости (на рисунке 4 силы упругости показаны стрелками). От внешнего слоя к нейтральному эти силы уменьшаются. Внутренний слой не испытывает заметных деформаций и не противодействует внешним силам, а поэтому является лишним в конструкции. Его обычно удаляют, заменяя стержни трубами, а бруски – тавровыми балками (рис. 5). Сама природа в процессе эволюции наделила человека и животных трубчатыми костями конечностей и сделала стебли злаков трубчатыми, сочетая экономию материала с прочностью и меткостью «конструкций».
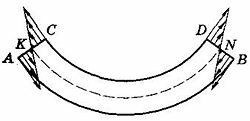
Рис. 4
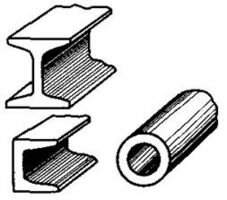
Рис. 5
Деформация кручения. Если на стержень, один из концов которого закреплен (рис. 6), подействовать парой сил, лежащей в плоскости поперечного сечения стержня, то он закручивается. Возникает, как говорят, деформация кручения.
Каждое поперечное сечение поворачивается относительно другого вокруг оси стержня на некоторый угол. Расстояние между сечениями не меняется. Таким образом, опыт показывает, что при кручении стержень можно представить как систему жестких кружков, насаженных центрами на общую ось. Кружки эти (точнее, сечения) поворачиваются на различные углы в зависимости от их расстояния до закрепленного конца. Слои поворачиваются, но на различные углы. Однако при этом соседние слои поворачиваются друг относительно друга одинаково вдоль всего стержня. Деформацию кручения можно рассматривать как неоднородный сдвиг. Неоднородность сдвига выражается в том, что деформация сдвига изменяется вдоль радиуса стержня. На оси деформация отсутствует, а на периферии она максимальна. На самом удаленном от закрепленного конца торце стержня угол поворота наибольший. Его называют углом кручения. Кручение испытывают валы всех машин, винты, отвертки и т.п.

Рис. 6
Основными деформациями являются деформации растяжения (сжатия) и сдвига. При деформации изгиба происходит неоднородное растяжение и сжатие, а при деформации кручения – неоднородный сдвиг.
| Вид деформации | Признаки |
|---|---|
| Растяжения | увеличивается расстояние между молекулярными слоями. |
| Сжатия | уменьшается расстояние между молекулярными слоями. |
| Кручения | поворот одних молекулярных слоев относительно других. |
| Изгиба | одни молекулярные слои растягиваются, а другие сжимаются или растягиваются, но меньше первых. |
| Сдвига | одни слои молекул сдвигаются относительно других. |
| Упругая | после прекращения воздействия тело полностью вос-станавливает первоначальную форму и размеры. |
| Пластичная | после прекращения воздействия тело не восстанавливает первоначальную форму или размеры. |
Силы упругости.
При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.
Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости.
Силы упругости препятствуют изменению размеров и формы тела. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. Например, со стороны упруго деформированной доски D на брусок С, лежащий на ней, действует сила упругости Fупр (рис. 7).
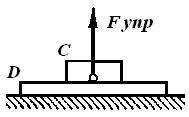
Рис. 7
Важная особенность силы упругости состоит в том, что она направлена перпендикулярно поверхности соприкосновения тел, а если идет речь о таких телах, как деформированные пружины, сжатые или растянутые стержни, шнуры, нити, то сила упругости направлена вдоль их осей.
В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела.
Силу, действующую на тело со стороны опоры или подвеса, называют силой реакции опоры или силой натяжения подвеса. На рисунке 8 приведены примеры приложения к телам сил реакции опоры (силы N1, N2, N3, N4 и N5) и сил натяжения подвесов (силы T1, T2, T3 и T4).
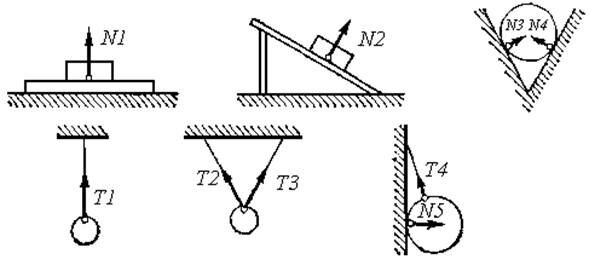
Рис. 8
Абсолютное и относительное удлинения
Линейная деформация (деформация растяжения) – деформация, при которой происходит изменение только одного линейного размера тела.
Количественно она характеризуется абсолютным Δl и относительным ε удлинением.
(~Delta l = |l — l_0|) ,
где Δl – абсолютное удлинение (м); l и l0 – конечная и начальная длина тела (м).
- Если тело растягивают, то l > l0 и Δl = l – l0;
- если тело сжимают, то l < l0 и Δl = –(l – l0) = l0 – l (рис. 9).
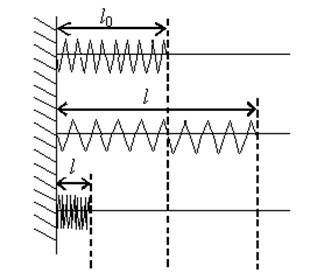
Рис. 9
(~varepsilon = frac{Delta l}{l_0}) или (~varepsilon = frac{Delta l}{l_0} cdot 100%) ,
где ε – относительное удлинение тела (%); Δl – абсолютное удлинение тела (м); l0 –начальная длина тела (м).
Закон Гука
Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид
(~F_{ynp} = k cdot Delta l) , (1)
где Fупр – модуль силы упругости, возникающей в теле при деформации (Н); Δl – абсолютное удлинение тела (м).
Коэффициент k называется жесткостью тела – коэффициент пропорциональности между деформирующей силой и деформацией в законе Гука.
Жесткость пружины численно равна силе, которую надо приложить к упруго деформируемому образцу, чтобы вызвать его единичную деформацию.
В системе СИ жесткость измеряется в ньютонах на метр (Н/м):
(~[k] = frac{[F_{ynp}]}{[Delta l]}) .
Коэффициент жесткости зависит от формы и размеров тела, а также от материала.
Закон Гука для одностороннего растяжения (сжатия) формулируют так:
сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.
Механическое напряжение.
Состояние упруго деформированного тела характеризуют величиной σ, называемой механическим напряжением.
Механическое напряжение σ равно отношению модуля силы упругости Fупр к площади поперечного сечения тела S:
(~sigma = frac{F_{ynp}}{S}) .
Измеряется механическое напряжение в Па: [σ] = Н/м2 = Па.
Наблюдения показывают, что при небольших деформациях механическое напряжение σ пропорционально относительному удлинению ε:
(~sigma = E cdot |varepsilon|) . (2)
Эта формула является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным.
Коэффициент пропорциональности Е в законе Гука называется модулем упругости (модулем Юнга). Экспериментально установлено, что
модуль Юнга численно равен такому механическому напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза.
Докажем это: Из закона Гука получаем, что (~E = frac{sigma}{varepsilon}) . Если модуль Юнга E численно равен механическому напряжению σ, то (~varepsilon = frac{Delta l}{l_0} = 1) . Тогда (~Delta l = l — l_0 = l_0 ; l = 2 l_0) .
Измеряется модуль Юнга в Па: [E] = Па/1 = Па.
Практически любое тело (кроме резины) при упругой деформации не может удвоить свою длину: значительно раньше оно разорвется. Чем больше модуль упругости Е, тем меньше деформируется стержень при прочих равных условиях (l0, S, F). Таким образом, модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения или сжатия.
Закон Гука, записанный в форме (2), легко привести к виду (1). Действительно, подставив в (2) (~sigma = frac{F_{ynp}}{S}) и (~varepsilon = frac{Delta l}{l_0}) , получим:
(~frac{F_{ynp}}{S} = E cdot frac{Delta l}{l_0}) или (~F_{ynp} = frac{E cdot S}{l_0} cdot Delta l) ,
где (~frac{E cdot S}{l_0} = k) .
Диаграмма растяжения
Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств (например, с помощью гидравлического пресса) подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения σ от относительного удлинения ε. Этот график называют диаграммой растяжения (рис. 10).
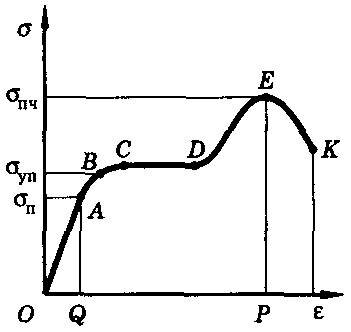
Рис. 10
Многочисленные опыты показывают, что при малых деформациях напряжение σ прямо пропорционально относительному удлинению ε (участок ОА диаграммы) – выполняется закон Гука.
Эксперимент показывает, что малые деформации полностью исчезают после снятия нагрузки (наблюдается упругая деформация). При малых деформациях выполняется закон Гука. Максимальное напряжение, при котором еще выполняется закон Гука, называется пределом пропорциональности σп. Он соответствует точки А диаграммы.
Если продолжать увеличивать нагрузку при растяжении и превзойти предел пропорциональности, то деформация становится нелинейной (линия ABCDEK). Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участок АВ графика). Максимальное напряжение, при котором еще не возникают заметные остаточные деформации, называется пределом упругости σуп. Он соответствует точке В диаграммы. Предел упругости превышает предел пропорциональности не более чем на 0,33%. В большинстве случаев их можно считать равными.
Если внешняя нагрузка такова, что в теле возникают напряжения, превышающие предел упругости, то характер деформации меняется (участок BCDEK). После снятия нагрузки образец не принимает прежние размеры, а остается деформированным, хотя и с меньшим удлинением, чем при нагрузке (пластическая деформация).
За пределом упругости при некотором значении напряжения, соответствующем точке С диаграммы, удлинение возрастает практически без увеличения нагрузки (участок CD диаграммы почти горизонтален). Это явление называется текучестью материала.
При дальнейшем увеличении нагрузки напряжение повышается (от точки D), после чего в наименее прочной части образца появляется сужение («шейка»). Из-за уменьшения площади сечения (точка Е) для дальнейшего удлинения нужно меньшее напряжение, но, в конце концов, наступает разрушение образца (точка К). Наибольшее напряжение, которое выдерживает образец без разрушения, называется пределом прочности. Обозначим его σпч (оно соответствует точке Е диаграммы). Его значение сильно зависит от природы материала и его обработки.
Чтобы свести к минимуму возможность разрушения сооружения, инженер должен при расчетах допускать в его элементах такие напряжения, которые будут составлять лишь часть предела прочности материала. Их называют допустимыми напряжениями. Число, показывающее, во сколько раз предел прочности больше допустимого напряжения, называют коэффициентом запаса прочности.
Обозначив запас прочности через n, получим:
(~n = frac{sigma_{np}}{sigma}) .
Запас прочности выбирается в зависимости от многих причин: качества материала, характера нагрузки (статическая или изменяющаяся со временем), степени опасности, возникающей при разрушении, и т.д. На практике запас прочности колеблется от 1,7 до 10. Выбрав правильно з?
