Модуль упругости при растяжении меди

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 января 2018;
проверки требуют 8 правок.
Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:
где:
В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука):
.
Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:
- Модуль Юнга (E) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия (удлинения). Часто модуль Юнга называют просто модулем упругости.
- Модуль сдвига или модуль жесткости (G или ) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига является одной из составляющих явления вязкости.
- Модуль объёмной упругости или Модуль объёмного сжатия (K) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля (для несжимаемой жидкости — бесконечен).
Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.
Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.
В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.
Модули упругости (Е) для некоторых веществ:
| Материал | Е, МПа | Е, кгс/см² |
|---|---|---|
| Алюминий | 70000 | 713 800 |
| Вода | 2030 | 20300 |
| Дерево | 10000 | 102 000 |
| Кость | 30000 | 305 900 |
| Медь | 100000 | 1 020 000 |
| Резина | 5 | 50 |
| Сталь | 200000 | 2 039 400 |
| Стекло | 70000 | 713 800 |
См. также[править | править код]
- Модуль Юнга
- Модуль сдвига G
- Жёсткость
- Предел текучести
- Упругость
- Предел прочности
- Упругие волны
- Уравнение Гассмана
- en:Dynamic modulus
Ссылки[править | править код]
- Free database of engineering properties for over 63,000 materials
- Расчёт модуля упругости по ПНАЭ Г-7-002-86
- Иомдина Е. Н. Механические свойства тканей глаза человека. (недоступная ссылка)
Литература[править | править код]
- Модули упругости // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1974. — Т. XVI. — С. 406. — 616 с.
- G. Mavko, T. Mukerji, J. Dvorkin. The Rock Physics Handbook. Cambridge University Press 2003 (paperback). ISBN 0-521-54344-4
Источник
Механические свойства меди Механические свойства различных марок меди при стандартных статических Механические свойства бескислородной меди М16 при стандартных 1. Табл. 1. Механические свойства | ||
Свойства | Состояние | |
деформированное | отожженое | |
Временное | 340…450 | 220…250 |
Предел текучести | 280-420 | 60-75 |
Относительное удлинение δ , % | 4…6 | 40…50 |
Относительное сужение ψ, % | 35…45 | 70…80 |
Твердость по Бринеллю, HB | 90…110 | 45 |
Предел выносливости σ-1, | 100…120 | 70…80 |
Ударная вязкость KCU, | 1,0 | 1,70 |
*kσ — коэффициент концентрации напряжений
Влияние степени холодной деформации и температуры отжига на механические
свойства меди показано на рис. 1 и 2.
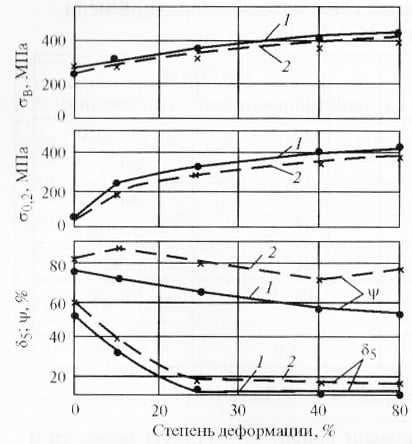
Рис. 1 Влияние степени холодной деформации (%) на механические свойства
меди:
1 — кислородсодержащей; 2 — раскисленной
фосфором, с высоким остаточным содержанием фосфора
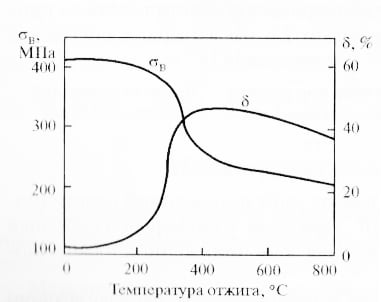
Рис. 2. Влияние
температуры отжига (в течение часа) на механические свойства
кислородсодержащей меди М1
Содержание кислорода в меди влияет на ударную вязкость и технологическую
пластичность.
Например, ударная вязкость горячекатаных медных полос (99.9%
Cu)
с различным содержанием кислорода составляет:
О2, % 0,026 0,030
0,034 0,042
KCU,кДж/м2
860 560
510 270
Влияние кислорода на технологическую пластичность на примере медной
проволоки диаметром
2,6
мм в твердом состоянии и с содержанием меди 99,90% следующее:
Способ получения | Число гибов при радиусе равном 5 мм | Число скручиваний загиба, на длине 152 мм |
Бескислородная | 12 | 92 |
Бескислородная | 7 | 45 |
Медь и многие ее сплавы имеют зоны пониженной пластичности («провала»
пластичности). При этом у кислородсодержащей меди наблюдается явно
выраженная зона пониженной пластичности при температурах 300…500°С; у
меди, раскисленной фосфором и с большим его остаточным содержанием
(0,04%), также наблюдается пониженная пластичность в этом интервале
температур. С повышением чистоты меди зона пониженной пластичности
уменьшается, а у бескислородной меди высокой чистоты (99,99%) эта зона
практически отсутствует. Зона пониженной пластичности отсутствует и у
меди, раскисленной бором (0,01% В).
При
отрицательных температурах медь имеет более высокие прочность и
пластичность, чем при температуре 20°С.
Механические свойства меди, на примере применяемой для электродов
контактной сварки, при высоких температурах приведены в табл. 2.
| Табл. 2. Механические свойства меди при высоких температурах | |||||||
| Свойства | Температура, °С | ||||||
| 20 | 200 | 300 | 400 | 500 | 600 | 700 | |
| Временное сопротивление σb , МПа | 220 | 200 | 150 | 110 | 70 | 50 | 30 |
| Предел текучести σ0,2 , Мпа | 60 | 50 | 50 | 40 | 30 | 20 | 10 |
| Относительное удлинение δ , % | 45 | 45 | 40 | 38 | 47 | 57 | 71 |
| Относительное сужение ψ, % | 90 | 88 | 77 | 73 | 86 | 100 | 100 |
| Твердость по Виккерсу, HV | 50 | 40 | 38 | 35 | 19 | 1 | 9 |
| Ударная вязкость KCU, МДж/м2 | 1,7 | 1,5 | 1,4 | 1,4 | 1,2 | 0,9 | 0,8 |
Длительная | — | — | — | 25 | 10 | 6 | 5 |
Характеристики
упругости.
Упругие свойства изотропного материала характеризуются модулями
нормальной упругости
Е
(модуль Юнга), сдвига
G
и объемного сжатия
Есж,
а также коэффициентом Пуассона (µ). Значения модулей
Е и
G
в интервале температур 300… 1300К уменьшаются по линейному закону.
Лишь в области низких температур наблюдается отклонение от равномерного
изменения модулей (табл. 3).
| Табл. 3. Модули упругости и сдвига меди при различных температурах | |||||||||
| Модули, ГПа | Температура, К | ||||||||
| 4,2 | 100 | 200 | 300 | 500 | 700 | 900 | 1100 | 1300 | |
| Е | 141 | 139 | 134 | 128 | 115 | 103 | 89,7 | 76,8 | 63,7 |
| G | 50 | 49,5 | 47,3 | 44,7 | 37,8 | 31 | 24,1 | 18,5 | 11,5 |
Регламентированные механические свойства продукции из меди при различных
способах изготовления, состояниях поставки и размерах приведены в табл.
4 — 7.
Как
правило, на лентах толщиной менее 0,5 мм, а также на лентах толщиной
0,5… 1,5 мм в мягком состоянии, используемых для штамповки, временное
сопротивление и относительное удлинение не определяют, а проводят
испытания на выдавливание лунки по Эриксену (см. табл. 5).
| Табл. 4. Плоский прокат из меди. Размеры и механические свойства | ||||||
| Продукция, стандарт или технические условия | Марка | Изгот. | Сост. пост. | Толщина, мм | Временное сопротивление σb , МПа | Относительное удлинение δ10, % |
| не менее | ||||||
| Плиты из раскисленной меди, ТУ 48-21-517-85 | M1p | ГК | — | 75…11О | 180 | 20 |
| Листы общего назначения, ГОСТ 1173-2006 | M1, M1p, М1ф, М2, М2р, М3, МЗр | ГК | — | 3…25 | 200 | 30 |
| ХК | М | 0,05… 12 | 200…260 | 36 | ||
| ПТ | 240…310 | 12 | ||||
| Тв | 290 | 3 | ||||
| Листы и полосы повышенного качества ТУ 48-21-664-79 | M1 | ЛХК | М | 3…8 | 200 | 36 |
| ЛГК | — | 8…10 | 200 | 30 | ||
| ПХК | М | 3…6 | 200 | 36 | ||
| Шины для электротехнических целей, ГОСТ 434-78 | M1 | ХК | М | св. 7 | — | 35 |
| Ленты общего назначения, ГОСТ 1173-2006 | M1, M1p, М1ф, М2, M2p, М3, МЗр | ХК | М | 0,1…6 | 200…260 | 36 |
| ПТ | 240…310 | 12 | ||||
| Тв | 290 | 3 | ||||
| Ленты для коаксиальных магистральных кабелей, ГОСТ 16358-79 | M1 | хк | М | 0,16…0,3 | 210 | δ5≥25 |
| Ленты для капсюлей, ГОСТ 1018-77 | M1, M1p, М2, M2p | ХК | М | 0,35…1,86 | 200 | 36 |
| Ленты для электротехн ических целей, ТУ 48-21-854-88 | M1, М2 | ХК | М | до 0,2 | — | — |
| 0,2…2,5 | — | 36 | ||||
| 2,5—3,53 | — | 36 | ||||
| 3,55…5,5 | — | 36 | ||||
| Тв | до 0,2 | 310 | — | |||
| 0,2…2.5 | 310 | — | ||||
| 2,5…3,53 | 284 | |||||
| 3,55…5,5 | 284 | — | ||||
| Фольга рулонная для технических целей, ГОСТ 5638-75 | M1, М2 | ХК | Тв | 0,015…0,05 | 290 | — |
| Условные обозначения: | ||||||
| ГК — горячекатаные; ХК — холоднокатаные; ЛХК листы холоднокатаные; Л ГК — листы горячекатаные; ПХК — полосы холоднокатаные; М — мягкое; ПТ — полутвердое; Тв — твердое. | ||||||
| Табл. 5. Характеристики холоднокатаных лент при испытании по Эриксену (радиус пуансона 10 мм) | ||||
| Ленты | Марка | Состояние | Толщина, мм | Глубина лунки, мм, не менее |
| Общего назначения, ГОСТ 1173-2006 | M1, M1p, М1p, М2, М2р, М3, МЗр | мягкое | 0,1…0,14 | 7 |
| 0,14…0,16 | 7 | |||
| 0,16…0,28 | 8 | |||
| 0,28…0,55 | 8,5 | |||
| 0,55…0,6 | 9 | |||
| 0,6…1,1 | 9,5 | |||
| 1,1…1,5 | 10 | |||
| Радиаторные, ГОСТ 20707-80 | M1, М2, М3 | мягкое | 0,06…0,07 | 4,5…9.0 |
| 0,08…0,09 | 6,0…9,0 | |||
| 0,1 | 7,5 | |||
| 0,12…0,15 | 7,5 | |||
| 0,17…0,25 | 8 | |||
| твердое | 0,1 | 1,5…3,5 | ||
| 0,12…0,15 | 1,5…3,5 | |||
| Для электротехнических целей, ТУ 48-21-854-88 | M1 | мягкое | 0,1…0,15 | 7,5 |
| 0,2…0,25 | 8 | |||
| 0,3…0,5 | 8,2 | |||
| 0,6…1 | 9,5 | |||
| Таблица 6. Трубы и трубки из меди. Размеры и механические свойства | ||||||
| Продукция, стандарт или технические условия | Марка | Изгот. | Сост. пост. | Диаметр, мм / Толщина стенки, мм | Временное сопротивление σb , МПа | Относительное удлинение δ10, % |
| не менее | ||||||
| Трубы общего назначения, ГОСТ 617-2006 | M1, M1p, М1ф, М2р, МЗр, М2, М3 | ХД | М | 3…360 / 0,8…10 | 200 | 35 |
| ПТ | 240 | 8 | ||||
| Тв | 280 | |||||
| Пр | — | до 200 / 5…30 | 190 | 30 | ||
| >200 / 5…30 | 180 | 30 | ||||
| Трубы квадратные и прямоугольные е круглым отверстием, ТУ48-21-497-81 | M1, M1p, М1ф, М2р, МЗр, М2, М3 | Т, П | М | b; h; d | 200 | 35 |
| 15…20,5; | ||||||
| 13.5…14; | ||||||
| 6…12,5 | ||||||
| Пр | b; h; d | 190 | 30 | |||
| 36…120; | ||||||
| 16…36; | ||||||
| 11…28 | ||||||
| Трубы медные, ТУ 48-21-482-85 | M1, M1p, М1ф, М2р, МЗр, М2, М3 | Пр | — | 30 / 9 | 190 | 30 |
| Трубки медные тонкостенные, ТУ 48-21-161-85 | M1, М2 | Т | М | 0,8…2 / 0,15…0,5 | 210 | 35 |
| Тв | — | 4 | ||||
| Трубки медные тонкостенные. ГОСТ 11383-75 | M1, М2, М3 | Т | М | 1,5…28 / 0,15…0,7 | 210 | 35 |
| Тв | 340 | 2 | ||||
| Трубы медные круглого сечения для воды и газа ГОСТ 52318-2005 | M1p, М1ф | Т | М | 6…22 / 0,5…1.5 | 220 | δ10≥40 |
| ПТ | 6…54 / 0,5…2 | 250 | δ10≥20 | |||
| Тв | 6…267 / 0,5…3 | 290 | δ10≥3 | |||
| Условные обозначения: | ||||||
| ХД — холоднодеформированные; Пр — прессованные; Т гянутые; | ||||||
| П — прокатанные: М — мягкое; ПТ — полутвердое; Тв — твердое; h, h,d — ширина, высота, диаметр отверстия. | ||||||
| Таблица 7. Прутки, катанка и проволока из меди. Размеры и механические свойства | ||||||
| Продукция,стандарт или технические условия | Марка | Изгот. | Сост. пост. | Размеры, мм | Временное сопротивление σb , МПа | Относительное удлинение δ10, % |
| не менее | ||||||
| Прутки квадратные, ТУ 48-21-97-72 | М2 | Пр | — | 42…94 | 200 | 30 |
| Прутки, IOCT 1535-2006 | M1, M1p, Мф, М2р, МЗр, М2, М3 | Т | М | 3…50 | 200 | 35 |
| ПТ | 240 | 10 | ||||
| Тв | 270 | 5 | ||||
| Пр | — | 20…50 | 190 | 30 | ||
| Профили из бескислородной меди, ТУ 48-21-637-79 | М0б | Т | М | b x h 11,4 x 8 | 200 | 38 |
| Проволока для заклепок, ТУ 48-21-456-2006 | M1, М2 | Т | Тв | d 1…2 | 240 | 8 |
| d 2…10,7 | 240 | 15 | ||||
| Проволока из бескислородной меди, ТУ 48-21-158-72 | М0б | Т | М | d 3,5;4,2 | 200 | 30 |
| Проволока крешерная, ГОСТ 4752-79 | М0б | ХД | Тв | d 3…10 | 320… | — |
| 360 | ||||||
| Проволока для электротехнических целей, ГОСТ 434-78 | М0, M1 | Т | М | d до 2,5 | — | 35 |
| d 2,5…7 | — | 35 | ||||
| d 7…10 | — | 35 | ||||
| d св. 10 | — | 35 | ||||
| Тв | d до 2,5 | 310 | — | |||
| d 2,5…7 | 290 | — | ||||
| d 7…10 | 270 | — | ||||
| d св. 10 | 270 | — | ||||
| Катанка медная, ТУ 16705.491-2001 | не ниже M1 | НЛ | — | d 8…23 | 160 | 35 |
| Условные обозначения: | ||||||
| Пр — прессованные; Т — тянутые; ХД — холоднодеформированная; НЛ — непрерывное литье и прокатка; | ||||||
| М — мягкое; ПТ — полутвердое; Тв — твердое; b — ширина; h — высота; d — диаметр. | ||||||
Источник
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Модуль Юнга
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (1012Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
E=α/ε
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Виды деформации
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Δl = α * (lF) / S
Величину, обратную α, и называют модулем Юнга:
1/α = E
Относительная деформация:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
ε=α σ
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
σ = ε/α = E ε
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Запас прочности
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
Источник
