Модуль упругости материала на растяжение

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 января 2018; проверки требуют 8 правок.
Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:
где:
В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука):
.
Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:
- Модуль Юнга (E) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия (удлинения). Часто модуль Юнга называют просто модулем упругости.
- Модуль сдвига или модуль жесткости (G или ) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига является одной из составляющих явления вязкости.
- Модуль объёмной упругости или Модуль объёмного сжатия (K) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля (для несжимаемой жидкости — бесконечен).
Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.
Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.
В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.
Модули упругости (Е) для некоторых веществ:
| Материал | Е, МПа | Е, кгс/см² |
|---|---|---|
| Алюминий | 70000 | 713 800 |
| Вода | 2030 | 20300 |
| Дерево | 10000 | 102 000 |
| Кость | 30000 | 305 900 |
| Медь | 100000 | 1 020 000 |
| Резина | 5 | 50 |
| Сталь | 200000 | 2 039 400 |
| Стекло | 70000 | 713 800 |
См. также[править | править код]
- Модуль Юнга
- Модуль сдвига G
- Жёсткость
- Предел текучести
- Упругость
- Предел прочности
- Упругие волны
- Уравнение Гассмана
- en:Dynamic modulus
Ссылки[править | править код]
- Free database of engineering properties for over 63,000 materials
- Расчёт модуля упругости по ПНАЭ Г-7-002-86
- Иомдина Е. Н. Механические свойства тканей глаза человека. (недоступная ссылка)
Литература[править | править код]
- Модули упругости // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1974. — Т. XVI. — С. 406. — 616 с.
- G. Mavko, T. Mukerji, J. Dvorkin. The Rock Physics Handbook. Cambridge University Press 2003 (paperback). ISBN 0-521-54344-4
Источник
Мо́дуль Ю́нга (синонимы: модуль продольной упругости, модуль нормальной упругости) — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации[1]. Обозначается большой буквой Е.
Назван в честь английского физика XIX века Томаса Юнга.
В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал деформируемой среды и процесса.
В Международной системе единиц (СИ) измеряется в ньютонах на квадратный метр или в паскалях. Является одним из модулей упругости.
Модуль Юнга рассчитывается следующим образом:
где:
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
где — плотность вещества.
Связь с другими модулями упругости[править | править код]
В случае изотропного тела модуль Юнга связан с модулем сдвига и модулем объёмной упругости соотношениями
и
где — коэффициент Пуассона.
Температурная зависимость модуля Юнга[править | править код]
Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости определяется как вторая производная от внутренней энергии по соответствующей деформации . Поэтому при температурах ( — температура Дебая)
температурная зависимость модуля упругости определяется простым соотношением
где
— адиабатический модуль упругости идеального кристалла при ; — дефект модуля, обусловленный тепловыми фононами; — дефект модуля, обусловленный тепловым движением электронов проводимости[2]
Значения модуля Юнга для некоторых материалов[править | править код]
Значения модуля Юнга для некоторых материалов приведены в таблице
См. также[править | править код]
- Закон Гука
Примечания[править | править код]
- ↑ Главный редактор А. М. Прохоров. Модули упругости // Физический энциклопедический словарь. — М.: Советская энциклопедия (рус.). — 1983. — Статьи в Физическом энциклопедическом словаре и Физической энциклопедии.
- ↑ Паль-Валь Л. Н., Семеренко Ю. А., Паль-Валь П. П., Скибина Л. В., Грикуров Г. Н. Исследование акустических и резистивных свойств перспективных хромо-марганцевых аустенитных сталей в области температур 5—300 К // Конденсированные среды и межфазные границы. — 2008. — Т. 10, вып. 3. — С. 226—235.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В. И. Анурьев; 8-е изд., перераб и доп. Под ред. И. Н. Жестковой. — М.: Машиностроение, 2001. — С. 34. ISBN 5-217-02963-3
- ↑ Галашев А. Е., Рахманова О. Р. Устойчивость графена и материалов на его основе при механических и термических воздействиях (рус.) // Успехи физических наук. — М.: РАН, ФИАН, 2014. — Т. 184, вып. 10. — С. 1051.
- ↑ В.Д. Нацик, П.П. Паль-Валь, Л.Н. Паль-Валь, Ю.А. Семеренко. Низкотемпературный a-пик внутреннего трения в ниобии и его связь с релаксацией кинков на дислокациях // ФНТ. — 2001. — Т. 27, вып. 5. — С. 547—557.
- ↑ П.П. Паль-Валь, В.Д. Нацик, Л.Н. Паль-Валь, Ю.А. Семеренко. Нелинейные акустические эффекты в монокристаллах ниобия, обусловленные дислокациями // ФНТ. — 2004. — Т. 30, вып. 1. — С. 115—125.
Литература[править | править код]
- Волькенштейн В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. — СПб.: Лань, 1999. — 328 с.
Ссылки[править | править код]
- Квазистатический модуль Юнга (код на Mathcad).
Источник
Предел прочности при растяжении
Предел прочности при растяжении (Tensile Strength at Yield) — одна из наиболее важных характеристик термопластов, это сопротивление, которое материал оказывает на напряжение растяжения. Оно определяется как наименьшее напряжение растяжения (сила, деленная на единицу площади поперечного разреза), требуемое, чтобы начать растягивать предмет.
Измеренное усилие делится на площадь поперечного сечения образца, получаемая величина, измеряемая в Н/мм² (а также в мегапаскалях МПа или гигапаскалях ГПа) и называется пределом прочности при растяжении.
Определение данного параметра проводят по международной методике ISO 527-1 (Пластики: определение параметров упругости) на т.н. разрывных машинах.
| Вложение 305 | Величина данного параметра определяет стойкость материала к статическим напряжениям, т.е. его прочность под постоянной растягивающей нагрузкой. В частности подобные напряжения испытывают конструкционные материалы для емкостного оборудования – одной из основных сфер применения инженерных термопластов. Значение данного параметра для различных термопластов – см. здесь. Помимо прочности при растяжении, для конструкционных материалов могут измеряться также прочности на сжатие, скручивание и т.д., однако для инженерных термопластов измерение данных параметров, как правило, не имеет практического смысла. |
Предел прочности при разрыве
Данные показатель называют также разрывным усилием (Tensile Strength at Break, Breaking Strength) и он также характеризует сопротивление, которое материал оказывает на напряжение растяжения. Оно определяется как наименьшее напряжение растяжения (сила, деленная на единицу площади поперечного разреза), требуемое, чтобы разрушить предмет.
Измеренное усилие делится на площадь поперечного сечения образца, получаемая величина, измеряемая в Н/мм² (а также в мегапаскалях МПа или гигапаскалях ГПа) и называется пределом прочности при разрыве.
Определение данного параметра проводят по международной методике ISO 527-1 на т.н. разрывных машинах в рамках единого теста с определением предела прочности при растяжении.
Значение данного параметра для различных термопластов – см. здесь.
Относительное удлинение при разрыве
Относительное удлинение (Elongation at Break) характеризует величину деформаций материала при растяжении. Данный показатель измеряется как отношение величины деформации образца к его первоначальной длине и измеряется в %.
Определение данного параметра проводят по международной методике ISO 527-1 на т.н. разрывных машинах в ходе тестов по определению пределов прочности при растяжении и разрыве.
Значение данного параметра для различных термопластов – см. здесь.
При сопоставлении этих показателей можно заметить что материалы с высокой прочностью к растяжениям и разрывам, как правило, имеют низкие показатели относительного удлинения и наоборот. Это позволяет делить термопласты на «прочные», которые выдерживают высокие механические нагрузки, но быстро ломаются при наступлении деформаций; и эластичные, которые не так прочны, однако способны сохранять свои прочностные свойства при деформациях.
Модуль упругости при растяжении
Модуль упругости при растяжении (Modulus of elasticity at tension, E-modulus) определяют как отношение приращения механического напряжения к соответствующему приращению относительного удлинения. Данный параметр характеризует сопротивление материала растяжению и измеряется в Н/мм².
Помимо модуля упругости при растяжении, могут также измеряться модули упругости при сжатии и сгибе, однако для инженерных термопластов именно первый показатель наиболее важен и имеет практическое применение, в частности, при статическом расчете безнапорных сварных емкостей из термопластов по методике DVS-2205.
Испытания проводятся по методике ISO 527-1 на том же оборудовании что и предел прочности при растяжении/разрыве. В отечественной практике также используется ГОСТ 9550-81 (Пластики. Метод определения модуля упругости при растяжении, сжатии и изгибе.)
Значение данного параметра для различных термопластов – см. здесь.
Источник
Определение прочности материала при растяжении проводится по ГОСТ 11262, а определение модуля упругости – по ГОСТ 9550-81.
Образцы для испытаний термопластов и армированных пластиков должны соответствовать типу и размерам, указанным на рисунке и в таблице.
Рисунок 1: Образцы для испытаний материалов на растяжение (Числовые значения параметров приведены в таблице 1)
Образец типа 1 применяют для испытаний пластмасс с высоким относительным удлинением при разрыве (полиэтилен, пластифицированный поливинилхлорид), образец типа 2 – для испытаний большинства материалов (термореактивные, термопластичные и слоистые пластики), образец типа 3 в форме полоски – для испытаний стеклопластиков.
Таблица 1
| Размеры образцов, мм | Образец типа | ||
| 1 | 2 | 3 | |
| Общая длина l1, не менее | 115 | 150 | 250 |
| Расстояние между метками, определяющими положение кромок зажимов на образце, l2 | 80±5 | 115±5 | 170±5 |
| Длина рабочей части l3 | 33±1 | 60±1 | – |
| Расчетная длина l | 25±1 | 50±1 | 50±1 |
| Ширина головки b1 | 25±0,5 | 20±0,5 | 25±0,5 |
| Ширина рабочей части b2 | 6±0,4 | 10±0,5 | – |
| Толщина h | 2±0,2(от 1 до 3) | 4±0,4(от 1 до 10) | 2±0,2(от 1 до 6) |
Диаграмму растяжения строят при нагружении образца до разрушения. Скорость нагружения – 2,0±0,4 мм/мин. По удлинению в момент разрушения Dl определяют относительно удлинение при разрыве e.
По максимальному значению нагрузки Fpвычисляют предел прочности при растяжении.
Удлинение измеряют прибором с погрешностью не более 2% в диапазоне 0,1–0,5 мм. База преобразователя перемещения L, устанавливаемого на образец, не менее 20 мм.
По диаграмме деформирования определяют значения нагрузок F1 и F2 и удлинение Dl1 и Dl2, соответствующих относительному удлинению 0,1% и 0,3% и рассчитывают модуль упругости при растяжении.
При невозможности записи диаграммы деформирования модуль упругости определяют при циклическом нагружении образца (до получения стабильных приращений) в диапазоне усилий F1 = (0,05–0,1)×Fр до F2 = 0,2×Fр. При значениях нагрузки F1 и F2 определяют приращение Dl на базе L.
Испытания полимерных материалов на растяжение: экспериментальная часть
Испытания на растяжение полимерных материалов проводят при температуре 23±2°С в соответствии с ГОСТ 11262–80 и ГОСТ 9550–81.
Перед испытанием замеряют ширину и толщину образцов в рабочей части с точностью до 0,01 мм не менее чем в трех местах и вычисляют площадь поперечного сечения. В расчет принимают наименьшую площадь поперечного сечения.
Перед испытанием на образец наносят необходимые метки (без повреждения образцов), ограничивающие его базу и положение кромок захватов (таблица).
Образцы закрепляют в зажимы испытательной машины по меткам, определяющим положение кромок зажимов, таким образом, чтобы продольные оси зажимов и ось образца совпадали между собой и с направлением движения подвижного зажима. Зажимы затягивают равномерно, чтобы не было проскальзывания образца в процессе испытания, но при этом не происходило его разрушение в месте закрепления. Далее настраивают прибор для замера деформаций.
Затем образец нагружают возрастающей нагрузкой, величину которой фиксируют по шкале динамометра. Скорость нагружения составляет 25 мм/мин при определении прочности и относительного остаточного удлинения. В момент разрушения фиксируют наибольшее усилие и определяют прочность при растяжении по формуле
где Fp – нагрузка, при которой образец разрушился, Н; S = b×h – начальное поперечное сечение образца, мм2; b, h – ширина и толщина образца соответственно, мм.
Образцы, разрушившиеся за пределами рабочей части, за результат не принимают.
По удлинению в момент разрушения Dl определяют относительное удлинение при разрыве e:
где Dl – изменение расчетной длины образца в момент разрыва, мм; l – расчетная длина, мм.
Модуль упругости определяют по формуле
где F1, F2 – значения нагрузок, соответствующих относительному удлинению 0,1% и 0,3%, Н; Dl1, Dl2 – удлинение при нагрузках F1, F2 соответственно, мм.
За результат измерения прочности, относительного удлинения и модуля упругости принимают среднее арифметическое значение для всех образцов.
Результаты испытаний заносят в протокол.
Образцы протоколов испытаний на растяжение
ПРОТОКОЛ № ____ от _____________
Испытания на растяжение по ГОСТ 11262–80
- ИСПЫТАТЕЛЬНАЯ МАШИНА (тип, номер, год выпуска, шкала)
- АППАРАТУРА: (измеритель удлинения, тип и основные характеристики)
- МАТЕРИАЛ: (тип, марка или состав связующего, ГОСТ, дата изготовления)
- ОБРАЗЦЫ: (тип, размеры, количество, метод изготовления)
- УСЛОВИЯ КОНДИЦИОНИРОВАНИЯ: температура 20 °С, относительная влажность 50% в течение 24 ч.
- УСЛОВИЯ ПРОВЕДЕНИЯ ИСПЫТАНИЯ: (температура, влажность, скорость нагружения)
- РЕЗУЛЬТАТЫ ИСПЫТАНИЙ:
| № п/п | l0, мм | Размеры образцов, мм | S0, мм2 | F, Н | sр, МПа | |
| h | b | |||||
| 1 | ||||||
| … | ||||||
| Среднее арифметическое значение, МПа | ||||||
| Среднее квадратическое отклонение | ||||||
| Коэффициент вариации, % | ||||||
Испытания провел:
ПРОТОКОЛ № ____ от _____________
Определения модуля упругости при растяжении по ГОСТ 9550–81
- ИСПЫТАТЕЛЬНАЯ МАШИНА (тип, номер, год выпуска, шкала)
- АППАРАТУРА: (измеритель удлинения, тип и основные характеристики)
- МАТЕРИАЛ: (тип, марка или состав связующего, ГОСТ, дата изготовления)
- ОБРАЗЦЫ: (тип, размеры, база, количество, метод изготовления)
- УСЛОВИЯ КОНДИЦИОНИРОВАНИЯ: температура 20 °С, относительная влажность 50 % в течение 24 часов.
- УСЛОВИЯ ПРОВЕДЕНИЯ ИСПЫТАНИЯ: (температура, влажность, скорость нагружения)
- РЕЗУЛЬТАТЫ ИСПЫТАНИЙ:
| № п/п | l0, мм | Размеры образцов, мм | S0, мм2 | Нагрузка, Н | Удлинение, мм | Ер, ГПа | |||
| h | b | F1 | F2 | l1 | l2 | ||||
| 1 | |||||||||
| … | |||||||||
| Среднее арифметическое значение | |||||||||
| Среднее квадратическое отклонение | |||||||||
| Коэффициент вариации, % | |||||||||
Испытания провел:
Читайте также: Механические свойства полимеров
Список литературы:
Пластмассы. Метод определения модуля упругости при растяжении, сжатии и изгибе: ГОСТ 9550–81. – Взамен ГОСТ 9550–71; введ. 01.07.1982. – М.: ИПК Изд-во стандартов, 2004. – 8 с.
Пластмассы. Метод испытания на растяжение: ГОСТ 11262–80. – Взамен ГОСТ 11262–76; введ. 01.12.1980. – М.: Изд-во стандартов, 1986.– 16 с.
Пластмассы. Методы механических испытаний. Общие требования: ГОСТ 14359–69. – Введен 01.01.1970. – М.: Изд-во стандартов, 1979.– 21 с.
Расчеты и испытания на прочность. Методы механических испытаний композиционных материалов с полимерной матрицей (композитов). Метод испытания плоских образцов на растяжение при нормальной, повышенной и пониженной температурах: ГОСТ 25.601–80. – Введен 01.07.81. – М.: Изд-во стандартов, 1980.– 16 с.
Автор: Кордикова Е.И., кандидат технических наук, доцент кафедры механики материалов и конструкций БГТУ
Источник: Композиционные материалы: Лабораторный практикум, 2007 год
Дата в источнике: 2007 год
Источник
Диаграммы напряжений
На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.
Тут может возникнуть вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления некоторого предела — сопротивления, существуют только в теории. В реальности большинство материалов обладают как упругими так и пластическими свойствами, что это за свойства, рассмотрим ниже на примере металлов.
Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.
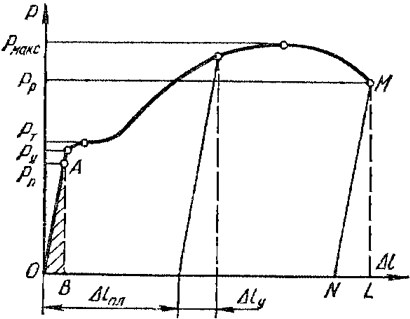
Рисунок 318.1. Диаграмма напряжений для стального образца.
На данной диаграмме мы видим 5 характерных точек:
1. Предел пропорциональности Рп (точка А)
Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:
σп = Рп/Fo (318.2.1)
Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:
Рп = kΔl (318.2.2)
где k — коэффициент жесткости:
k = EF/l (318.2.3)
где l — длина образца, F — площадь сечения, Е — модуль Юнга.
Модули упругости
Главными характеристиками упругих свойств материалов являются модуль Юнга Е (модуль упругости первого рода, модуль упругости при растяжении), модуль упругости второго рода G (модуль упругости при сдвиге) и коэффициент Пуассона μ (коэффициент поперечной деформации).
Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности
Модуль Юнга также определяется опытным путем при испытании стандартных образцов на растяжение. Так как нормальные напряжения в материале равны силе, деленной на начальную площадь сечения:
σ = Р/Fо (318.3.1), (317.2)
а относительное удлинение ε — отношению абсолютной деформации к начальной длине
εпр = Δl/lo (318.3.2)
то модуль Юнга согласно закону Гука можно выразить так
Е = σ/εпр = Plo/FoΔl = tgα (318.3.3)
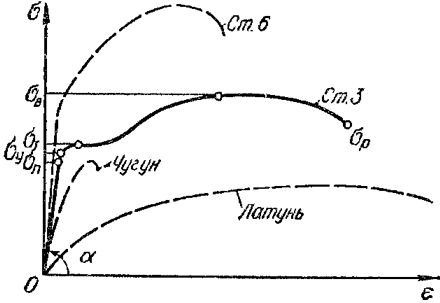
Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов
Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным
Под воздействием нагрузок не только увеличивается длина образца, но и уменьшается площадь рассматриваемого поперечного сечения (если предположить, что объем материала в области упругих деформаций остается постоянным, то значит увеличение длины образца приводит к уменьшению площади сечения). Для образца, имеющего круглое сечение, изменение площади сечения можно выразить так:
εпоп = Δd/do (318.3.4)
Тогда коэффициент Пуассона можно выразить следующим уравнением:
μ = εпоп/εпр (318.3.5)
Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига
Модуль сдвига G может быть определен опытным путем при испытании образцов на кручение.
При угловых деформациях рассматриваемое сечение перемещается не линейно, а под некоторым углом — углом сдвига γ к начальному сечению. Так как касательные напряжения равны силе, деленной на площадь в плоскости которой действует сила:
т = Р/F (318.3.6)
а тангенс угла наклона можно выразить отношением абсолютной деформации Δl к расстоянию h от места фиксации абсолютной деформации до точки, относительно которой осуществлялся поворот:
tgγ = Δl/h (318.3.7)
то при малых значениях угла сдвига модуль сдвига можно выразить следующим уравнением:
G = т/γ = Ph/FΔl (318.3.8)
Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны между собой следующим отношением:
Е = 2(1 + μ)G (318.3.9)
Значения постоянных Е, G и µ приводятся в таблице 318.1
Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов
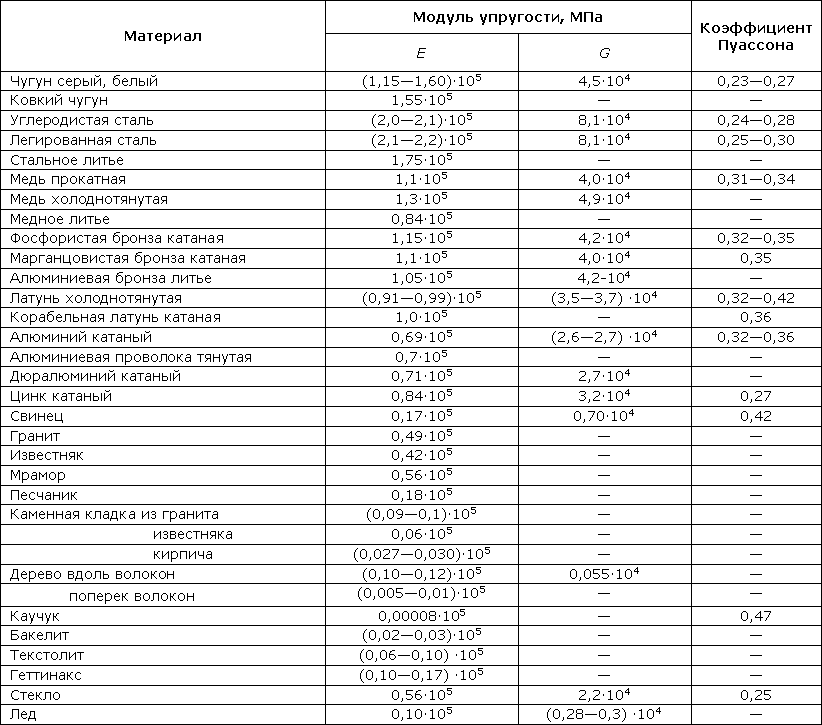
Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления различных строительных материалов меняются и более точные значения модулей упругости следует уточнять по действующим в настоящий момент нормативным документам. Модули упругости бетона зависят от класса бетона и потому здесь не приводятся.
Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. Между тем на диаграмме напряжений можно выделить еще несколько точек:
2. Предел упругости Ру
Нормальные напряжения в поперечном сечении образца при достижении предела упругости будут равны:
σу = Ру/Fo (318.2.4)
Предел упругости ограничивает участок на котором появляющиеся пластические деформации находятся в пределах некоторой малой величины, нормированной техническими условиями (например 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается соответственно допуску σ0.001, σ0.01 и т.д.
3. Предел текучести Рт
σт = Рт/Fo (318.2.5)
Ограничивает участок диаграммы на котором деформация увеличивается без значительного увеличения нагрузки (состояние текучести). При этом по всему объему образца происходит частичный разрыв внутренних связей, что и проводит к значительным пластическим деформациям. Материал образца полностью не разрушается, но его начальные геометрические размеры претерпевают необратимые изменения. На отшлифованной поверхности образцов наблюдаются фигуры текучести — линии сдвигов (открытые профессором В. Д. Черновым). Для различных металлов углы наклона этих линий различны, но находятся в пределах 40-50о. При этом часть накопленной потенциальной энергии необратимо расходуется на частичный разрыв внутренних связей. При испытании на растяжение принято различать верхний и нижний пределы текучести — соответственно наибольшее и наименьшее из напряжений, при которых возрастает пластическая (остаточная) деформация при почти постоянной величине действующей нагрузки.
На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.
Некоторые материалы не имеют выраженной площадки текучести. Для них за условный предел текучести σ0.2 принимается напряжение, при котором остаточное удлинение образца достигает значения ε ≈0,2%.
4. Предел прочности Рмакс (временное сопротивление)
Нормальные напряжения в поперечном сечении образца при достижении предела прочности будут равны:
σв = Рмакс/Fo (318.2.6)
После преодоления верхнего предела текучести (на диаграммах напряжения не показан) материал снова начинает сопротивляться нагрузкам. При максимальном усилии Рмакс начинается полное разрушение внутренних связей материала. При этом пластические деформации концентрируются в одном месте, образуя в образце так называемую шейку.
Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.
В таблицах 318.2 — 318.5 приведены ориентировочные величины пределов прочности для некоторых материалов:
Таблица 318.2 Ориентировочные пределы прочности на сжатие (временные сопротивления) некоторых строительных материалов.

Примечание: Для металлов и сплавов значение пределов прочности следует определять согласно нормативных документов. Значение временных сопротивлений для некоторых марок стали можно посмотреть здесь.
Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для некоторых пластмасс

Таблица 318.4. Ориентировочные пределы прочности для некоторых волокон
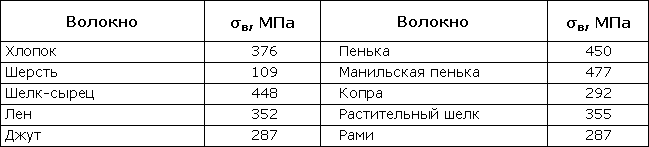
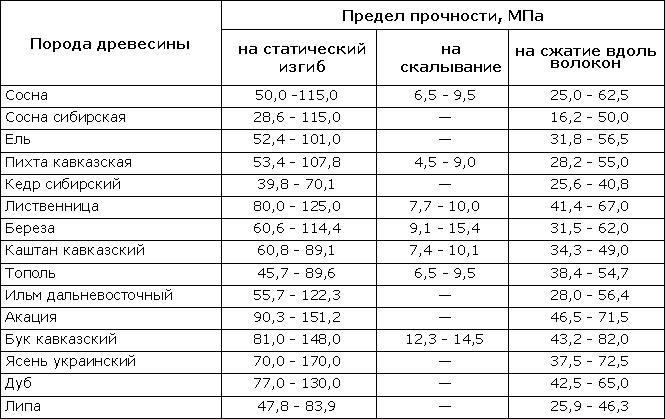
Таблица 318.5. Ориентировочные пределы прочности для некоторых древесных пород
5. Разрушение материала Рр
Если посмотреть на диаграмму напряжений, то создается впечатление, что разрушение материала наступает при уменьшении нагрузки. Такое впечатление создается потому, что в результате образования «шейки» значительно изменяется площадь сечения образца в районе «шейки». Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, то будет видно, что напряжения в рассматриваемом сечении увеличиваются до некоторого предела:
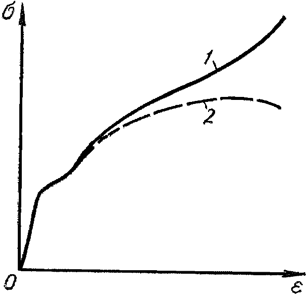
Рисунок 318.3. Диаграмма напряжений: 2 — по отношению к начальной площади поперечного сечения, 1 — по отношению к изменяющейся площади сечения в районе шейки.
Тем не менее более правильным является рассмотрение прочностных характеристик материала по отношению к площади первоначального сечения, так как расчетами на прочность изменение первоначальной геометрической формы редко предусматривается.
Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:
ψ = 100(Fo — F)/Fo (318.2.7)
где Fo — начальная площадь поперечного сечения образца (площадь поперечного сечения до деформации), F — площадь поперечного сечения в районе «шейки». Чем больше значение ψ, тем более ярко выражены пластические свойства материала. Чем меньше значение ψ, тем больше хрупкость материала.
Если сложить разорванные части образца и измерить его удлинение, то выяснится, что оно меньше удлинения на диаграмме (на длину отрезка NL), так как после разрыва упругие деформации исчезают и остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.
За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 некоторая точка между пределом текучести и пределом прочности), и затем разгрузить его, то в образце останутся пластические деформации, но при повторном загружении через некоторое время предел упругости станет выше, так как в данном случае изменение геометрической формы образца в результате пластических деформаций становится как бы результатом действия внутренних связей, а изменившаяся геометрическая форма, становится начальной. Этот процесс загрузки и разгрузки материала можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:

Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям)
Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Тем не менее при повышении прочности металла путем наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому полезным как правило считается относительно небольшой наклеп.
Работа деформации
Прочность материала тем выше, чем больше внутренние силы взаимодействия частиц материала. Поэтому величина сопротивления удлинению, отнесенная к единице объема материала, может служить характеристикой его прочности. В этом случае предел прочности не является исчерпывающей характеристикой прочностных свойств данного материала, так как он характеризует только поперечные сечения. При разрыве разрушаются взаимосвязи по всей площади сечения, а при сдвигах, которые происходят при всякой пластической деформации, разрушаются только местные взаимосвязи. На разрушение этих связей затрачивается определенная работа внутренних сил взаимодействия, которая равна работе внешних сил, затрачиваемой на перемещения:
А = РΔl/2 (318.4.1)
где 1/2 — результат статического действия нагрузки, возрастающей от 0 до Р в момент ее приложения (среднее значение (0 + Р)/2)
При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение:
А = ηРмаксΔlмакс (318.4.2)
где η — коэффициент полноты диаграммы, равный отношению площади всей диаграммы, ограниченной кривой АМ и прямыми ОА, MN и ON, к площади прямоугольника со сторонами 0Рмакс (по оси Р) и Δlмакс (пунктир на рис. 318.1). При этом надо вычесть работу, определяемую площадью треугольника MNL (относящуюся к упругим деформациям).
Работа, затрачиваемая на пластические деформации и разрушение образца, является одной из важных характеристик материала, определяющих степень его хрупкости.
Деформация сжатия
Деформации сжатия подобны деформациям
