Модуль силы упругости при растяжении

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 января 2018;
проверки требуют 8 правок.
Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:
где:
В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука):
.
Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:
- Модуль Юнга (E) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия (удлинения). Часто модуль Юнга называют просто модулем упругости.
- Модуль сдвига или модуль жесткости (G или ) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига является одной из составляющих явления вязкости.
- Модуль объёмной упругости или Модуль объёмного сжатия (K) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля (для несжимаемой жидкости — бесконечен).
Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.
Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.
В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.
Модули упругости (Е) для некоторых веществ:
| Материал | Е, МПа | Е, кгс/см² |
|---|---|---|
| Алюминий | 70000 | 713 800 |
| Вода | 2030 | 20300 |
| Дерево | 10000 | 102 000 |
| Кость | 30000 | 305 900 |
| Медь | 100000 | 1 020 000 |
| Резина | 5 | 50 |
| Сталь | 200000 | 2 039 400 |
| Стекло | 70000 | 713 800 |
См. также[править | править код]
- Модуль Юнга
- Модуль сдвига G
- Жёсткость
- Предел текучести
- Упругость
- Предел прочности
- Упругие волны
- Уравнение Гассмана
- en:Dynamic modulus
Ссылки[править | править код]
- Free database of engineering properties for over 63,000 materials
- Расчёт модуля упругости по ПНАЭ Г-7-002-86
- Иомдина Е. Н. Механические свойства тканей глаза человека. (недоступная ссылка)
Литература[править | править код]
- Модули упругости // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1974. — Т. XVI. — С. 406. — 616 с.
- G. Mavko, T. Mukerji, J. Dvorkin. The Rock Physics Handbook. Cambridge University Press 2003 (paperback). ISBN 0-521-54344-4
Источник
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Механика
Силы в природе
1.12. Сила упругости. Закон Гука
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
| Рисунок 1.12.1. Деформация растяжения ( x > 0 ) и сжатия ( x < 0 ). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
| Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
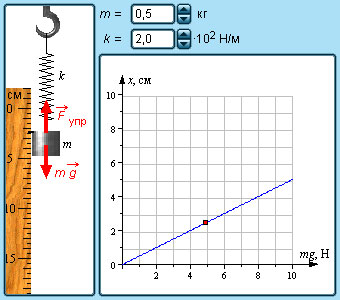 |
Модель. |
Источник
Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие
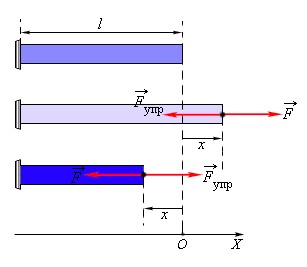
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Закон Гука
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k — коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
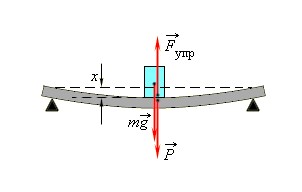
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр.
Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.
Источник
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.
Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.
Деформация.
Силы упругости возникают при деформациях тел. Деформация — это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб.
Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.
Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.
Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:
1. действует между соседними слоями деформированного тела и приложена к каждому слою;
2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры).
Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил
выходит далеко за рамки школьной программы.
В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.
Закон Гука.
Деформация называется малой, если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.
Закон Гука. Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину , сила упругости даётся формулой:
(1)
где — коэффициент жёсткости пружины.
Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.
Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):
 |
| Рис. 1. Закон Гука |
Коэффициент жёсткости — о угловой коэффициент в уравнении прямой . Поэтому справедливо равенство:
,
где — угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .
Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 — это лишь небольшой начальный участок криволинейного графика, описывающего зависимость от при всех значениях деформации .
Модуль Юнга.
В частном случае малых деформаций стержней имеется более детальная формула, уточняющая общий вид ( 1 ) закона Гука.
Именно, если стержень длиной и площадью поперечного сечения растянуть или сжать
на величину , то для силы упругости справедлива формула:
.
Здесь — модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.
Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.
Источник
Дата введения 1982-07-01
Постановлением государственного комитета СССР по стандартам от 26 августа 1981 г. N 4058 дата введения установлена 01.07.82
Ограничение срока действия снято по протоколу N 5-94 Межгосударственного совета по стандартизации, метрологии и сертификации (ИУС 11-12-94)
ВЗАМЕН ГОСТ 9550-71
ИЗДАНИЕ (май 2004 г.) с Поправкой (ИУС 11-89).
Настоящий стандарт распространяется на пластмассы и устанавливает методы определения модуля упругости при растяжении, сжатии и изгибе.
Стандарт не распространяется на ячеистые пластмассы и пленки из пластмасс.
Стандарт полностью соответствует СТ СЭВ 2345-80.
Термины, применяемые в настоящем стандарте, и их пояснения приведены в приложении.
1. МЕТОД ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ПРИ РАСТЯЖЕНИИ
1.1. Сущность метода
Сущность метода заключается в определении модуля упругости при растяжении как отношения приращения напряжения к соответствующему приращению относительного удлинения, установленному настоящим стандартом.
1.2. Отбор образцов
1.2.1. Для испытания применяют образцы по ГОСТ 11262-80.
1.2.2. Количество образцов, взятых для испытания одной партии материала, а для анизотропных материалов в каждом из выбранных направлений, должно быть не менее 3.
1.3. Аппаратура
Для проведения испытания применяют аппаратуру по ГОСТ 11262-80, при этом испытательная машина должна обеспечивать скорость раздвижения зажимов (1,0±0,5)% в минуту, а прибор для измерения удлинения должен обеспечивать измерение с погрешностью не более 0,002 мм.
1.4. Подготовка к испытанию
1.4.1. Перед испытанием образцы кондиционируют в стандартной атмосфере по ГОСТ 12423-66 не менее 16 ч, если в нормативно-технической документации на конкретную продукцию нет других указаний.
1.4.2. Перед испытанием измеряют толщину и ширину образца по ГОСТ 11262-80.
1.5. Проведение испытания
1.5.1. Испытание проводят при температуре и относительной влажности, указанных в нормативно-технической документации на конкретную продукцию.
Если в нормативно-технической документации на конкретную продукцию нет других указаний, то испытание проводят в соответствии с ГОСТ 12423-66 при температуре (23±2) °С и относительной влажности (50±5)%.
1.5.2. Образец закрепляют в машину так, чтобы продольные оси зажимов и ось образца совпадали с линией, соединяющей точки крепления зажимов на испытательной машине.
1.5.3. На образце, закрепленном в зажимах, проводят установку и настройку прибора для измерения удлинения.
1.5.4. Образец нагружают при скорости раздвижения зажимов испытательной машины, обеспечивающей скорость деформации образца (1,0±0,5)% в минуту. Нагружение осуществляют до величины относительного удлинения 0,5%.
Если образцы разрушаются до достижения относительного удлинения 0,5%, нагружение проводят до меньшей величины деформации, установленной в нормативно-технической документации на конкретную продукцию.
1.5.5. Графическую запись нагрузки и деформации проводят в следующем масштабе:
100-150 мм на диаграмме должно соответствовать 0,4% относительного удлинения;
не менее 100 мм на диаграмме должно соответствовать приращению нагрузки, соответствующему увеличению относительного удлинения на 0,4%.
1.6. Обработка результатов
1.6.1. По диаграмме определяют значения нагрузки, соответствующие величинам относительного удлинения 0,1 и 0,3%. Допускаются меньшие значения относительного удлинения для образцов, предусмотренных в п.1.5.4.
1.6.2. Модуль упругости при растяжении () в МПа вычисляют по формуле
,
где — нагрузка, соответствующая относительному удлинению 0,3%, Н;
— нагрузка, соответствующая относительному удлинению 0,1%, Н;
— расчетная длина образца, мм;
— площадь начального поперечного сечения образца, мм;
— удлинение, соответствующее нагрузке , мм;
— удлинение, соответствующее нагрузке ,
мм.
1.6.3. За результат испытания принимают среднеарифметическое значение всех параллельных определений.
1.6.4. Величину стандартного отклонения вычисляют по ГОСТ 14359-69.
1.6.5. Результаты испытания записывают в протокол, который должен содержать следующие данные:
наименование и марку пластмассы и номер партии;
метод испытания;
наименование испытательной машины;
тип и марку прибора для измерения деформации;
условия проведения испытания (скорость нагружения, температура, графическая запись и т.д.);
тип испытуемого образца (форма, размеры);
условия подготовки испытуемого образца;
количество образцов, взятых для испытания;
среднеарифметическое определяемого показателя и стандартное отклонение;
дату испытания;
обозначение настоящего стандарта.
2. МЕТОД ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ПРИ СЖАТИИ
2.1. Сущность метода
Сущность метода заключается в определении модуля упругости при сжатии как отношения приращения напряжения к соответствующему приращению относительной деформации сжатия, установленному настоящим стандартом.
2.2. Отбор образцов
2.2.1. Для испытания применяют образцы по ГОСТ 4651-82. База измерения деформации должна составлять не менее 10 мм и не более высоты образца при измерении деформации прибором, установленным на образце.
При изготовлении образцов из изделий толщиной менее 5 мм используют образцы в форме прямоугольных пластин размерами (80±2)х(10,0±0,5) мм, а толщина образца равна толщине изделия. Для армированных пластмасс ширина образцов равна (15,0±0,5) мм. Для предотвращения потери устойчивости при испытании таких образцов применяют приспособление (черт.1).
Черт.1. Приспособление для испытания на сжатие образцов толщиной менее 5 мм
Приспособление для испытания на сжатие образцов толщиной менее 5 мм
Черт.1
2.2.2. Количество образцов должно соответствовать п.1.2.2.
2.3. Аппаратура
Для проведения испытания применяют аппаратуру по ГОСТ 4651-82, при этом испытательная машина должна обеспечивать скорость сближения опорных площадок со скоростью деформации образца (1,0±0,5)% в минуту, а прибор для измерения деформации сжатия должен обеспечивать измерение с погрешностью не более 0,002 мм.
2.4. Подготовка к испытанию
2.4.1. Перед испытанием образцы кондиционируют в стандартной атмосфере по ГОСТ 12423-66 не менее 16 ч, если в нормативно-технической документации на конфетную продукцию нет других указаний.
2.4.2. Перед испытанием измеряют размеры образцов по ГОСТ 4651-82.
2.5. Проведение испытания
2.5.1. Испытания проводят при температуре и относительной влажности, указанных в п.1.5.1.
2.5.2. Образец устанавливают на опорных плитах испытательной машины так, чтобы продольная ось образца совпадала с направлением действия силы.
2.5.3. Устанавливают прибор для измерения деформации. Деформацию при сжатии определяют измерением расстояния между площадками или по изменению базы на образце (см. п.2.2.1).
2.5.4. Образец нагружают при скорости сближения площадок испытательной машины, обеспечивающей скорость деформации образца (1,0±0,5)% в минуту. Нагружение осуществляют до величины деформации 0,5%.
Если образцы разрушаются до достижения относительной деформации 0,5%, нагружение осуществляют до меньшей величины деформации, установленной в нормативно-технической документации на конкретную продукцию.
2.5.5. Графическую запись нагрузки и деформации проводят в соответствии с п.1.5.5 при значениях относительной деформации сжатия, равных значениям относительного удлинения, указанных в п.1.5.5.
2.6. Обработка результатов
2.6.1. По диаграмме определяют значения нагрузки, соответствующие величинам относительной деформации 0,1 и 0,3%.
Допускаются меньшие значения относительной деформации при сжатии для образцов, предусмотренных в п.2.5.4.
2.6.2. Модуль упругости при сжатии () в МПа вычисляют по формуле
,
где — нагрузка, соответствующая относительной деформации 0,3%, Н;
— нагрузка, соответствующая относительной деформации 0,1%, Н;
— начальная высота образца или базы, мм;
— площадь начального поперечного сечения образца, мм;
— изменение высоты или базы, соответствующее нагрузке , мм;
— изменение высоты или базы, соответствующее нагрузке, ,
мм.
2.6.3. За результат испытания принимают среднеарифметическое значение всех параллельных определений.
2.6.4. Величину стандартного отклонения вычисляют, как указано в п.1.6.4.
2.6.5. Результаты испытания оформляют протоколом, как указано в п.1.6.5.
3. МЕТОД ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ПРИ ИЗГИБЕ
3.1. Сущность метода
Сущность метода заключается в определении модуля упругости при изгибе как отношения приращения напряжения к соответствующему приращению относительной деформации, установленному настоящим стандартом.
3.2. Отбор образцов
3.2.1. Для испытания применяют образцы по ГОСТ 4648-71.
3.2.2. Количество образцов должно соответствовать п.1.2.2.
3.3. Аппаратура
Для проведения испытания применяют аппаратуру по ГОСТ 4648-71, при этом испытательная машина должна обеспечивать скорость сближения нагружающего наконечника и опор, соответствующую скорости деформации образца (1,0±0,5)% в минуту, а прибор для измерения деформации образца должен обеспечивать измерение с погрешностью не более 0,01 мм.
3.4. Подготовка к испытанию
3.4.1. Перед испытанием образцы кондиционируют в стандартной атмосфере по ГОСТ 12423-66 не менее 16 ч, если в нормативно-технической документации на конкретную продукцию нет других указаний.
3.4.2. Перед испытанием измеряют размеры образцов по ГОСТ 4648-71.
3.5. Проведение испытания
3.5.1. Испытания на изгиб проводят двумя методами:
А — при нагружении по трехточечной схеме (черт.2);
Б — при нагружении по четырехточечной схеме (черт.3).
Черт.2. Трехточечная схема нагружения при изгибе
Трехточечная схема нагружения при изгибе
Метод А
Черт.2
Черт.3. Четырехточечная схема нагружения при изгибе
Четырехточечная схема нагружения при изгибе
Метод Б
— нагрузка; — расстояние между опорами; — прогиб; — эпюра момента
Черт.3
При методе А испытуемый образец нагружают наконечником в середине расстояния между опорами.
При методе Б испытуемый образец нагружают парой наконечников, расположенных в средней трети расстояния между опорами.
Выбор метода предусматривается в нормативно-технической документации на конкретную продукцию.
Прогиб измеряют:
в методе А — в середине расстояния между опорами (черт.2). Величину прогиба оценивают по величине перемещения подвижной части нагружающего устройства;
в методе Б — в соответствии с черт.3.
3.5.2. Испытания проводят при температуре и относительной влажности, указанных в п.1.5.1.
3.5.3. Расстояние между опорами () устанавливают в зависимости от толщины образца () от 15 до 17 мм и измеряют с погрешностью не более 0,5%.
3.5.4. На образце, лежащем на опорах, осуществляют установку и настройку прибора для измерения прогиба.
3.5.5. Образцы нагружают при скорости сближения нагружающего наконечника и опор, обеспечивающей скорость деформации образца (1,0±0,5)% в минуту.
Нагружение осуществляют до величины относительной деформации крайних волокон 0,5%.
Относительную деформацию крайних волокон () вычисляют по формуле
для метода А
;
для метода Б
,
где — значение прогиба, мм;
— толщина образца, мм;
— расстояние между опорами, мм.
Если образцы разрушаются до достижения относительной деформации крайних волокон 0,5%, нагружение осуществляют до меньшей величины деформации, установленной в нормативно-технической документации на конкретную продукцию.
3.5.6. Графическую запись нагрузки и деформации проводят в соответствии с п.1.5.5 при значениях прогиба, соответствующих значениям относительной деформации крайних волокон, указанных в п.1.5.5.
3.6. Обработка результатов
3.6.1. По диаграмме определяют значения нагрузки и прогиба, соответствующие значениям относительной деформации крайних волокон 0,1 и 0,3%.
Допускаются меньшие значения относительной деформации при изгибе для образцов, предусмотренных в п.3.5.5.
3.6.2. Модуль упругости при изгибе () в МПа вычисляют по формуле
для метода А
;
для метода Б
,
где — расстояние между опорами, мм;
— нагрузка при величине относительной деформации крайних волокон 0,3%, Н;
— нагрузка при величине относительной деформации крайних волокон 0,1%, Н;
— ширина образца, мм;
— толщина образца, мм;
— прогиб образца, соответствующий относительной деформации крайних волокон 0,3%, мм;
— прогиб образца, соответствующий относительной деформации крайних волокон 0,1%, мм
.
3.6.3. За результат испытания принимают среднеарифметическое значение всех параллельных определений.
3.6.4. Величину стандартного отклонения вычисляют, как указано в п.1.6.4.
3.6.5. Результаты испытания оформляют протоколом, как указано в п.1.6.5.
ПРИЛОЖЕНИЕ (справочное). Термины, применяемые в настоящем стандарте, и их пояснения
ПРИЛОЖЕНИЕ
Справочное
Понятие | Обозначение | Единица измерения | Определение |
Модуль упругости | МПа | Мера жесткости материала, характеризующаяся сопротивлением развитию упругих деформаций. | |
при растяжении | МПа | Модуль упругости определяют как отношение приращения напряжения к соответствующему приращению деформации | |
при сжатии | МПа | ||
при изгибе | МПа | ||
2. Скорость деформации | мин | Изменение относительной деформации растяжения или сжатия в единицу времени. Скорость деформации при растяжении и сжатии определяют как отношение скорости перемещения подвижного элемента испытательной машины () к длине образца между кромками зажимов или сжимающими площадками. При изгибе вычисляют по формуле для метода А ; для метода Б , где — скорость относительной деформации крайних волокон образца, равная 0,01 мин; — расстояние между опорами, мм; — толщина образца, мм. |
ПРИЛОЖЕНИЕ. (Поправка).
Текст документа сверен по:
официальное издание
М.: ИПК Издательство стандартов, 2004
Источник
