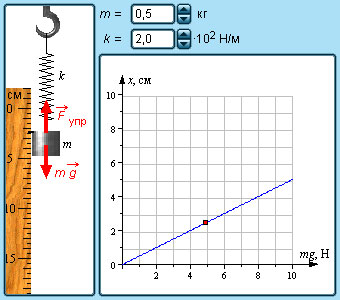
Модуль растяжения пружины формула
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Механика
Силы в природе
1.12. Сила упругости. Закон Гука
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
| Рисунок 1.12.1. Деформация растяжения ( x > 0 ) и сжатия ( x < 0 ). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
| Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
 |
Модель. |
Источник
Сил упругости возникает при деформации физического тела, то есть когда изменяются размеры и форма тела. Эта сила направлена в сторону, противоположную силе, создающей деформацию. На примере пружины выясним как сила упругости связана с величиной деформации. Рассмотрим также причины возникновения упругих сил.

Закон Гука
Пружину можно сжимать, растягивать, изгибать или скручивать. В каждом из этих случаев будут возникать силы упругости, стремящиеся вернуть форму и размеры пружины в начальное состояние. Для понимания основных закономерностей будем рассматривать только линейные сжатия и растяжения (вдоль оси х). Для вычисления сил при деформациях изгибов и скручивании требуется применение более сложного математического аппарата.

Рис. 1. Деформации растяжения и сжатия пружины.
Если начальная длина, ненапряженной пружины, равна L0, то для малых деформаций выполняется закон Гука, открытый экспериментально:
$ F_уп = − k * Δх $ (1),
где, в формуле силы упругости пружины:
Fуп — сила упругости пружины, Н;
k — коэффициент жесткости пружины, Н/м;
Δх —величина деформации (дельта икс), м.
Величина малых деформаций должна быть намного меньше начальной длины пружины:
$ Δх
Рис. 2. Портрет Роберта Гука.
Этот фундаментальный закон был открыт английским ученым Робертом Гуком в 1660г. Кроме этого он сделал много других замечательных изобретений и экспериментов:
- открыл эффект образования цветов тонких пленок, которое в оптике называется явлением интерференции;
- предложил модель волнообразного распространения света;
- сформулировал предположение о связи теплоты с движением частиц, из которых состоит тело;
- изобрел спиральную пружину для регулировки часов, усовершенствовал барометр, гигрометр, анемометр.
Источник силы упругости
Происхождение сил упругости связано с электромагнитным взаимодействием молекул и атомов. Когда происходит увеличение размеров пружины (растяжении), то силы взаимного притяжения “пытаются” восстановить начальные размеры. При сжатии пружины начинают работать силы отталкивания. Когда тело не деформировано, расстояние между молекулами соответствует равенству сил притяжения и отталкивания.
Динамометры
Упругие свойства пружин используются в приборах для измерения силы. Обычно динамометр состоит из двух основных частей: пружины (упругий элемент) и шкалы устройства, на которой нанесены цифровые значения силы или массы, если этот прибор предназначен для бытового применения. Измеряемое усилие прикладывается к пружине, которая деформируется и сдвигает стрелку прибора вдоль отсчетной шкалы.

Рис. 3. Пружинные динамометры.
Хотя закон Гука и считается универсальным, но диапазон деформаций в котором он выполняется сильно отличается для разных тел. Например, в металлических проволоках (прямолинейных) и стержнях максимальная величина относительной деформации (отношение Δх к L0), для которой еще будет справедлив закон Гука, составляет не более 1%. При больших деформациях наступают необратимые разрушения материалов.
Что мы узнали?
Итак, мы узнали, что сила упругости пружины прямо пропорциональна величине деформации тела и направлена в сторону, обратную направлению сдвига пружины. Силы упругости связаны с электромагнитным взаимодействием молекул и атомов. При сжатии включается механизм отталкивания электрических одноименных зарядов. При растяжении — начинает работать механизм притяжения разноименных зарядов.
Тест по теме
Оценка доклада
Средняя оценка: 4.7. Всего получено оценок: 75.
Источник
Определение и формула жесткости пружины
Определение
Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.
Чаще всего ее обозначают ${overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.
Рассмотрим пружину, на которую действует растягивающая сила ($overline{F}$), которая направлена вертикально вниз (рис.1).
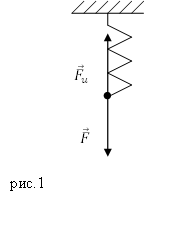
Силу $overline{F }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${overline{F}}_u$), уравновешивающая силу $overline{F }$. Если деформация является небольшой и упругой, то удлинение пружины ($Delta l$) прямо пропорционально деформирующей силе:
[overline{F}=kDelta lleft(1right),]
где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.
Жесткость (как свойство) — это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости — это основная характеристика жесткости (как свойства тела).
Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:
[k=frac{Gd^4}{8d^3_pn}left(2right),]
где $G$ — модуль сдвига (величина, зависящая от материала); $d$ — диаметр проволоки; $d_p$ — диаметр витка пружины; $n$ — количество витков пружины.
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
[left[kright]=left[frac{F_{upr }}{x}right]=frac{left[F_{upr }right]}{left[xright]}=frac{Н}{м}.]
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Формула жесткости соединений пружин
Пусть $N$ пружин соединены последовательно. Тогда жесткость всего соединения равна:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}+dots =sumlimits^N_{ i=1}{frac{1}{k_i}left(3right),}]
где $k_i$ — жесткость $i-ой$ пружины.
При последовательном соединении пружин жесткость системы определяют как:
[k=k_1+k_2+dots +sumlimits^N_{i=1}{k_i}left(4right).]
Примеры задач с решением
Пример 1
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac{Н}{м}. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.
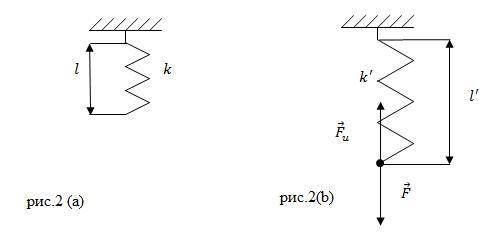
Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
[k=k’left(1.1right).]
При упругих деформациях выполняется закон Гука:
[F=kDelta l left(1.2right).]
Из (1.2) найдем удлинение пружины:
[Delta l=frac{F}{k}left(1.3right).]
Длина растянутой пружины равна:
[l’=l+Delta l=l+frac{F}{k}.]
Вычислим новую длину пружины:
[l’=0,01+frac{2}{10}=0,21 left(мright).]
Ответ. 1) $k’=10 frac{Н}{м}$; 2) $l’=0,21$ м
Пример 2
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?
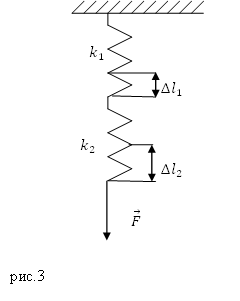
Решение. Если пружины соединены последовательно, то деформирующая сила ($overline{F}$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:
[F=k_1Delta l_1left(2.1right).]
Для второй пружины запишем:
[F=k_2Delta l_2left(2.2right).]
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
[k_1Delta l_1=k_2Delta l_2left(2.3right).]
Из равенства (2.3) получим удлинение первой пружины:
[Delta l_1=frac{k_2Delta l_2}{k_1}.]
Ответ. $Delta l_1=frac{k_2Delta l_2}{k_1}$
Читать дальше: формула закона Архимеда.
Источник
Главная
Расчет
пружин
10.
Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765-86 в
ред. 1990г.
Пружина сжатия
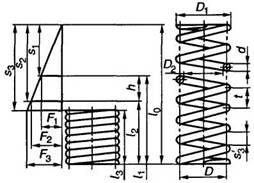
Пружина растяжения
Наименование | Обозначение | Расчетные |
1. Сила пружины | F1 | Принимаются в зависимости от нагрузки пружины |
2. Сила пружины при рабочей деформации (соответствует наибольшему принудительному | F2 | |
3. Рабочий ход | h | |
4. Наибольшая нагружении или разгрузке, м/с | Vmax | |
5. Выносливость | NF | |
6. Наружный | D1 | Предварительно назначают с учетом конструкции таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
7. Относительный растяжения служит | δ | δ = 1-F2/F3. (1) Для пружин сжатия классов I и IIδ=0,05…0,25; для пружин растяжения для одножильных пружин класса IIIδ=0,10…0,40; для трехжильных класса IIIδ=0,15…0,40 |
8. Сила пружины | F3 | F3=F2/(1-δ) (2) Уточняется по таблицам ГОСТ 13766-86-ГОСТ |
9. Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н | F0 | F0= (0,1… 0,25) F3 |
10. Диаметр | d | Выбирается по таблицам ГОСТ 13764-86-ГОСТ |
11. Диаметр | d1 | |
12. Жесткость | c1 | |
13. Максимальная | s’3 (при F0=0) s»3 (при F0>0) | Выбирается по таблицам ГОСТ 13764-86-ГОСТ |
14. Максимальное (Коэффициент k см. | τ3 | Назначается по табл. 2 ГОСТ 13764-86. При проверке Для трехжильных пружин |
15. Критическая скорость пружины сжатия, м/с (Максимальная скорость меньше vK, т.е. vK | vк | Для трехжильных пружин |
16. Модуль сдвига, | G | Для пружинной стали G = 7,85·104 |
17. Динамическая | Р | p = γ/g, где g-ускорение свободного падения, м/с2; γ — удельный вес, Н/м3. Для пружинной стали р = 8·103 |
18. Жесткость | с | Для пружин с предварительным напряжением Для трехжильных пружин |
19. Число рабочих | n | n = c1/c (7) |
20. Полное число | n1 | n1 = n+ n2, (8) где n2 — число опорных витков |
21. Средний | D | D = D1 – d = D2 + d Для трехжильных пружин D = D1– d1= D2+ |
22. Индекс пружины | i | i = D/d (10) Для трехжильных пружин i= D/d1 (10а) Рекомендуется назначать от 4 до 12 |
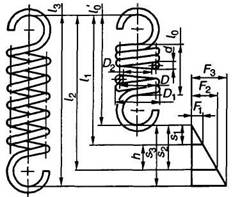
Наименование | Обозначение | Расчетные | ||||||
23. Коэффициент расплющивания учитывающий увеличение сечения витка вдоль оси пружины | Δ | Для трехжильного троса с углом свивки по таблице, приведенной ниже | ||||||
i | 40 | 45 | 50 | 55 | 60 | 7,0 и более | ||
Δ | 1,029 | 1,021 | 1,015 | 1,010 | 1,005 | 1,000 | ||
24. | s1 | s1=F1/c (11) | ||||||
25. Рабочая | s2 | s2= F2/c (12) | ||||||
26. Максимальная | s3 | s3= F3/c (13) | ||||||
27. Длина пружины | l3 | l3 = (n1 + 1 – n3)d, где n3 — число обработанных Для трехжильных пружин l3 = (n + l)d1Δ. Для пружин растяжения с зацепами l3 = l0 + s3 | ||||||
28. Длина пружины | l0 | l0=l3+s3 | ||||||
29. Длина пружины | l0′ | l0′ = (n1+1)d (15а) | ||||||
30. Длина пружины | 1l | l1 = l0-s1. Для пружин растяжения l1= l0+s1(16а) | ||||||
31. Длина пружины | l2 | l2=l0-s2. Для пружин растяжения l2=l0+s2 | ||||||
32. Шаг пружины в | t | t = s’3+d. (18) Для трехжильных пружин t = s’3+d1Δ. Для пружин растяжения t = d(18б) | ||||||
33. Напряжение в | τ1 | |||||||
34. Напряжение в | τ2 | |||||||
35. Коэффициент, | k | Для трехжильных пружин где | ||||||
36. Длина | l | |||||||
37. Масса пружины | m | |||||||
38. Объем, | V | |||||||
39. Зазор между витком пружины | λ | Устанавливается в зависимости от формы | ||||||
40. Внутренний | D2 | D2=D1-2d (25) | ||||||
41. Временное сопротивление | Rm | Устанавливается при испытаниях проволоки по ГОСТ 9389-75 и ГОСТ 1071-81 | ||||||
42. Максимальная или работа деформации, | Для пружин сжатия и растяжения без предварительного для пружин растяжения с предварительным | |||||||
Методика
определения размеров пружин по ГОСТ 13765-86.
1. Исходными величинами для определения
размеров пружин являются силы F1 и F2, рабочий ход h,
наибольшая скорость перемещения подвижного конца пружины при нагружении или
при разгрузке vmах,
выносливость NF и наружный диаметр пружины D1 (предварительный).
Если задана только одна сила F2,
то вместо рабочего хода h для подсчета берут величину рабочей деформации s2,
соответствующую заданной силе.
2. По величине заданной выносливости NF
предварительно определяют принадлежность пружины к соответствующему классу по
табл. 1.
3. По заданной силе F2 и крайним
значениям инерционного зазора δ вычисляют по формуле (2) значение силы F3.
4. По значению F3, пользуясь табл.
2, предварительно определяют разряд пружины.
5. По табл. 11-17 находят строку, в которой наружный
диаметр витка пружины наиболее близок к предварительно заданному значению D1.
В этой же строке находят соответствующие значения силы F3 и диаметра
проволоки d.
6. Для пружин из закаливаемых марок сталей
максимальное касательное напряжение τ3 находят по табл. 2, для
пружин из холоднотянутой и термообработанной τ3
вычисляют с
учетом значений временного сопротивления Rm. Для холоднотянутой проволоки Rm определяют из ГОСТ
9389-75, для термообработанной — из ГОСТ 1071-81.
7. По полученным значениям F3 и
τ3, a также по заданному значению F2 по формулам (5)
и (5а) вычисляют критическую скорость vK и
отношение vmax/vK,
подтверждающее или
отрицающее принадлежность пружины к предварительно
установленному классу.
При несоблюдении условий vmax/vK<1 пружины I и II классов относят к
последующему классу или повторяют расчеты, изменив исходные условия. Если
невозможно изменение исходных условий, работоспособность обеспечивается
комплектом запасных пружин.
8. По окончательно установленному классу и разряду
в соответствующей таблице на параметры витков пружин, помимо ранее найденных
величин F3, D1, и d, находят величины c1 и s3,
после чего остальные размеры пружины и габариты узла вычисляют по формулам
(6)… (25).
Примеры
определения размеров пружин и формулы для проверочных расчетов жесткости и
напряжений
Пример 1. Пружина сжатия.
Дано: F1 = 20Н; F2 =
80Н; h = 30мм; D1 = 10… 12мм; vmax
= 5м/с; NF≥ 1 · 107.
По табл. 1 убеждаемся, что при заданной
выносливости NF пружину следует отнести к классу 1.
По формуле (2), пользуясь интервалом значений
δ от 0,05 до 0,25 (см. п. 7 табл. 10), находим граничные значения силы F3,
а именно:
В интервале от 84 до 107Н (ГОСТ 13766-86)
пружин класса I, разряда 1 имеются следующие силы F3: 85; 90; 95;
100 и 106Н (табл. 11).
Исходя из заданных размеров
диаметра и стремления обеспечить наибольшую критическую скорость, останавливаемся на витке со следующими
данными (номер позиции 355):
F3 = 106Н; d = 1,80мм; D1
= 12мм; с1 = 97,05Н/мм; s’3=
1,092мм.
Учитывая, что для пружин класса I норма
напряжений τ = 0,3Rm (см. табл. 2), находим, что для найденного
диаметра проволоки из углеродистой холоднотянутой стали расчетное напряжение
τ3 = 0,3·2100 = 630Н/мм2.
Принадлежность к классу I проверяем определением
отношения vmax/vK,
для чего предварительно определяем критическую скорость по формуле (5) при
δ = 0,25:
Полученная величина свидетельствует о наличии
соударения витков в данной пружине, и, следовательно, требуемая выносливость
может быть не обеспечена. Легко убедиться, что при меньших значениях силы F3
отношение vmax /vк будет еще больше отличаться от единицы
и указывать на еще большую интенсивность соударения витков.
Используем пружины класса II. Заданному
наружному диаметру и найденным выше силам F3 соответствует виток с
данными по ГОСТ 13770-86 (см. табл. 14, позиция 303): F3=95,0H;
d=1,4мм; D1=11,5мм; с1=36,58Н/мм;
s’3=2,597мм.
Учитывая норму напряжений для пружин класса
IIτ3 = 0,5Rm, находим τ3 =
0,5×2300= 1150Н/мм2.
По формуле (2) вычисляем δ = 1-F2/F3
= 1 – 80/95 = 0,16 и находим vKи
vmax /vK,
с помощью которых определяем принадлежность пружин ко II классу:
Полученная величина указывает на отсутствие
соударения витков. Следовательно, выбранная пружина удовлетворяет заданным условиям.
Пружины класса II относятся к разряду ограниченной выносливости, поэтому
следует учитывать комплектацию машины запасными пружинами с учетом опытных
данных.
Определение остальных размеров производим по
формулам табл. 10.
По формуле (6) находим жесткость пружины:
Число рабочих витков пружины определяем по
формуле (7):
n= c1/c = 36,58/2,0 = 18,29 ≈
18,5.
Уточняем жесткость пружины:
c = c1/n= 36,68/18,5 = 1,977 ≈
2,0Н/мм.
При полутора нерабочих витках полное число витков
находим по формуле (8):
n1 = n + n2 =18,5 +
1,5= 20.
По формуле (9) определяем средний диаметр
пружины:
D = 11,5 — 1,4 = 10,1мм.
Деформации, длины и шаг пружины вычисляем по
формулам (11)-(18):
На этом определение размеров пружины и
габарита узла (размер li) заканчивается.
Следует отметить, что некоторое увеличение
выносливости может быть достигнуто при использовании пружины с большей
величиной силы F3, чем найденная в
настоящем примере. С целью выяснения габаритов, занимаемых такой пружиной,
проведем анализ:
остановимся, например, на витке со следующими
данными по ГОСТ 13770-86 (см. табл. 14, позиция 313): F3 = 106Н; d =
1,4мм; D1 = 10,5мм; с1 =
50,01Н/мм; s3′ = 2,119мм.
Находим τ3 = 1150Н/мм2 и производим расчет в той же
последовательности:
Очевидно, что у этой пружины создается
большой запас на несоударяемость витков.
Далее в рассмотренном ранее порядке находим
n= 50,01/2,0 = 25,01 ≈ 25,0.
Уточненная жесткость с =50,01/25,0 ≈
2,0Н/мм;
Таким образом, устанавливаем, что применение
пружины с более высокой силой F3 хотя и привело к большему запасу на
несоударяемость витков, но оно сопровождается
увеличением габарита узла (размер l1) на 15,3мм. Можно показать,
что если выбрать виток с большим диаметром, например D1=16мм (см.
табл. 14, номер позиции 314), то тогда потребуется расширить узел по диаметру,
но при этом соответственно уменьшится размер l1.
Пример 2. Пружина сжатия.
Дано: F1 = 100Н; F2 =
250Н; h = 100мм; D1 = 15…25мм; vmax
= 10м/с.
Независимо от заданной выносливости на
основании формулы (5) можно убедиться, что при значениях 8, меньших 0,25
[формула (1)], все одножильные пружины, нагружаемые со скоростью vmax более 9,4м/с,
относятся к III классу.
По формуле (2) с учетом диапазона значений
δ для пружин класса III от 0,1 до 0,4 [формула (1)] находим границы сил F3:
Верхние значения силы F3, как
видно из табл. 2, не могут быть получены из числа одножильных конструкций,
поэтому с учетом коэффициентов δ = 0,15…0,40 [формула (1)] для
трехжильных пружин устанавливаем новые пределы F3, по формуле (2):
F3 = 294…417H.
Для указанного интервала в ГОСТ 13774-86
имеются витки со следующими силами F3: 300; 315; 335; 375 и 400Н (табл. 16а).
Исходя из заданных размеров диаметра и
наименьших габаритов узла, предварительно останавливаемся на витке со
следующими данными (номер позиции 252): F3 = 300Н; d=1,4мм; d1=3,10мм;
D1 = 17мм; с1 = 50,93Н/мм; s’3
= 5,890мм.
Согласно ГОСТ 13764-86 для пружин класса
IIIτ3 = 0,6Rm. Используя ГОСТ 9389-75, определяем
напряжение для найденного диаметра проволоки:
τ3 = 0,6 · 2300 = 1380Н/мм3.
Принадлежность к классу проверяем путем
определения величины отношения vmax/vK, для чего предварительно находим 8 и критическую
скорость по формулам (1), (2) и (5а):
Полученное неравенство свидетельствует о
наличии соударения витков и о принадлежности пружины к классу III.
Определение остальных параметров производится
по формулам табл. 10.
По формуле (6) находим жесткость:
Число рабочих витков пружины вычисляют по
формуле (7):
Уточненная жесткость:
Полное число витков находят по формуле (8):
n1 = n + 1,5 = 34,0 + 1,5 = 35,5.
По формуле (9а) определяют средний диаметр
пружины:
D = D1 – d1 = 17 — 3,10
= 13,90мм.
Деформации, длины и шаг пружины находят по
формулам табл. 10:
Проанализируем пружины, соответствующие трем
ближайшим значениям F3, взятым из ГОСТ 13774-86 (пружины класса III, разряда 1) для
рассмотренного случая (табл. 16а).
Вычисления, проделанные в аналогичном
порядке, показывают, что для трех соседних сил F3 образуется шесть
размеров пружин, удовлетворяющих требованиям по величине наружного диаметра.
Сведения о таких пружинах приведены ниже.
F3,H | 300 | 315 | 335 | |||
d, мм | 1,4 | 1,6 | 1,4 | 1,6 | 1,4 | 1,6 |
d1, мм | 3,10 | 3,50 | 3,10 | 3,50 | 3,10 | 3,50 |
D1, мм | 17,0 | 24,0 | 16,0 | 22,0 | 15,0 | 21,0 |
vmax/vK | 1,43 | 1,50 | 1,16 | 1,21 | 0,942 | 0,984 |
l0, мм | 317,0 | 273,9 | 355,1 | 309,0 | 405,1 | 337,0 |
l1,мм | 250,4 | 207,2 | 288,4 | 242,3 | 338,4 | 270,3 |
l2, мм | 150,4 | 107,2 | 188,4 | 142,3 | 238,4 | 170,3 |
n1 | 36,0 | 20,0 | 44,5 | 27,0 | 56,0 | 31,0 |
V,мм3 | 57000 | 93000 | 58000 | 92000 | 60000 | 93000 |
Из этих данных следует, что с возрастанием F3
уменьшается отношение vmax/vK и, в частности, может быть устранено
соударение витков, но вместе с этим возрастают габариты по размерам l1.
С возрастанием диаметров пружин габариты по
размерам 1Х уменьшаются, однако существенно возрастают объемы пространств, занимаемые
пружинами.
Следует отметить, что если бы для рассматриваемого
примера, в соответствии с требованиями распространенных классификаций, была
выбрана пружина класса I, то при одинаковом диаметре гнезда (D1 ≈
18мм) даже самая экономная из них потребовала бы длину гнезда l1 =
546мм, т.е. в 2,2 раза больше, чем рассмотренная выше. При этом она была бы в
11,5 раза тяжелее и, вследствие малой критической скорости (vK
= 0,7м/с), практически неработоспособной при заданной скорости нагружения 10м/с.
Пример 3. Пружина растяжения.
Дано: F1=250Н; F2=800Н;
h=100мм; D1=28…32мм; NF≥ 1 · 105.
На основании ГОСТ 13764-86 по величине NF
устанавливаем, что пружина относится к классу II (см. табл. 1.) По формуле (2)
находим силы F3, соответствующие предельной деформации:
В интервале сил 842…889Н в ГОСТ 13770-86
для пружин класса II, разряда 1 (номер пружины 494) имеется виток со следующими
параметрами: F3=850Н; D1=30мм; d = 4,5мм; с1 = 242,2Н/мм; s’3 = 3,510мм.
По заданным параметрам с помощью формулы (6)
определяем жесткость пружины:
Число рабочих витков находим по формуле (7):
Деформации и длины пружины вычисляют по
формулам [( 11Н17а)]:
Размер l2 с учетом конструкций
зацепов определяет длину гнезда для размещения пружины растяжения в узле.
Размер l3 с учетом конструкций
зацепов ограничивает деформацию пружины растяжения при заневоливании.
Трехжильные пружины (угол свивки
24°).
Жесткость
где
Напряжение
Полученные значения жесткости должны
совпадать с вычисленными по формуле (6).
Полученные значения
напряжений должны совпадать с указанными в ГОСТ 13764-86 для соответствующих
разрядов с отклонениями не более ±10%.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика
Теория машин и механизмов
Источник
