Мягкая сталь при растяжении
Если подвергнуть образец растяжению, последовательно увеличивая нагрузку Р, и производить при этом замеры получающихся удлинений ∆l, то можно построить опытную диаграмму растяжения, откладывая удлинение в функции нагрузки.
Для удобства сравнения эту диаграмму выражают в напряжениях и относительных удлинениях:
где σ — нормальное напряжение;
F — первоначальная площадь сечения образца; ε — относительное удлинение в процентах;
l0 — первоначальная длина образца.
Величина относительного удлинения зависит от длины и поперечного сечения образца и увеличивается с уменьшением отношения
. Поэтому для сохранения сравнимости результатов испытаний установлены два типа образцов — длинный и короткий — с соотношениями между длиной и площадью сечения1
Опытная диаграмма растяжения малоуглеродистой стали марки Ст. 3 показана на фигуре.
Диаграмма растяжения стали марки Ст. 3
Вначале зависимость между напряжениями и относительными удлинениями определяется законом прямой линии, т. е. они пропорциональны между собой.
Это выражается линейным уравнением (зависимость Гука)
где Е — постоянный коэффициент пропорциональности, называемый модулем упругости при растяжении. Для стали Е = 2 100 000 кг/см2.
Пропорциональная зависимость между деформацией и напряжением имеет предел. То наибольшее напряжение в материале, при котором начинается отклонение от прямолинейной зависимости, называется пределом пропорциональности σпц.
Несколько выше этой точки лежит предел упругости σуп, соответствующий наибольшей деформации, которая полностью исчезает после разгрузки. Точное определение этой точки на кривой опытным путем затруднительно, поскольку она фиксируется моментом начала получения остаточных деформаций после снятия нагрузки, что означает переход материала в пластическую стадию.
Для малоуглеродистых сталей при нагружении выше предела пропорциональности кривая диаграммы растяжения отходит от прямой и, плавно поднимаясь, делает скачок (образуя характерный «зуб»), после чего с незначительными колебаниями идет параллельно горизонтальной оси. Образец удлиняется без приращения нагрузки, материал течет. То нормальное напряжение, практически постоянное, при котором происходит течение материала, называется пределом текучести σт.
Горизонтальный участок диаграммы, называемый площадкой текучести, для малоуглеродистых сталей находится в пределах относительных удлинений от ε = 0,2% до ε = 2,5%. Наличие у материала площадки текучести является положительным фактором в работе стальных конструкций.
В других сталях, не малоуглеродистых, переход в пластическую стадию происходит постепенно, без площадки текучести и без «зуба». Для них предел упругости и предел текучести, таким образом, принципиально не отличаются друг от друга. За предел текучести этих сталей принимается то напряжение, при котором остаточная деформация достигает 0,2%.
При снятии нагрузки с образца, получившего пластическую деформацию, диаграмма разгрузки идет по прямой С — D параллельно упругой прямой нагрузки.
Когда относительное удлинение достигает определенной величины (ε ≈ 2,5% для Ст. 3), материал прекращает течь и становится опять способным к сопротивлению. Он как бы самоупрочняется. Однако зависимость между напряжениями и деформациями подчиняется уже криволинейному закону, с быстрым нарастанием деформаций, после чего в образце образуется шейка и, наконец, происходит полное разрушение его.
Предельная сопротивляемость материала, которая характеризует его прочность, определяется наибольшим напряжением в процессе разрушения. Это напряжение называется пределом прочности σпч (временным сопротивлением); оно условно; поскольку при построении диаграммы растяжения напряжения, относят к первоначальной площади сечения образца, не учитывая сужения и образования шейки.
Полное остаточное удлинение, замеренное после разрушения, является мерой пластичности стали.
Таким образом, важнейшими показателями механических свойств, характеризующими работу стали, являются: предел текучести, предел прочности и относительное удлинение. Эти показатели, так же как и химический состав, указываются в сертификатах, которые сопровождают каждую партию поставляемого металла.
Государственным стандартом на поставку строительной стали гарантируются следующие ее механические характеристики.
Таблица Показатели механических свойств строительных сталей
1 Н. А. Шапошников, Механические испытания металлов, Машгиз, 1951.
«Проектирование стальных конструкций»,
К.К.Муханов
Источник
Лабораторная работа № 1
Цель работы – изучить поведение малоуглеродистой стали при растяжении и определить ее механические характеристики.
Основные сведения
Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.
Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.
В таких случаях, кроме металлографических исследований, определяются главные механические характеристики на образцах, взятых из зоны разрушения конструкции. Образцы изготавливаются по ГОСТ 1497-84 и могут иметь различные размеры и форму (рис. 1.1).
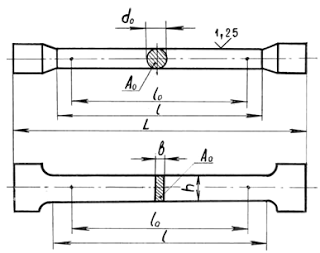
Рис. 1.1. Образцы для испытания на растяжение
Между расчетной длиной образца lо и размерами поперечного сечения Ао (или dо для круглых образцов) выдерживается определенное соотношение:
В испытательных машинах усилие создается либо вручную — механическим приводом, либо гидравлическим приводом, что присуще машинам с большей мощностью.
В данной работе используется универсальная испытательная машина УММ-20 с гидравлическим приводом и максимальным усилием 200 кН, либо учебная универсальная испытательная машина МИ-40КУ (усилие до 40 кН).
Порядок выполнения и обработка результатов
Образец, устанавливаемый в захватах машины, после включения насоса, создающего давление в рабочем цилиндре, будет испытывать деформацию растяжения. В измерительном блоке машины есть шкала с рабочей стрелкой, по которой мы наблюдаем рост передаваемого усилия F.
Зависимость удлинения рабочей части образца от действия растягивающей силы во время испытания отображается на миллиметровке диаграммного аппарата в осях F-Δl (рис. 1.2).
В начале нагружения деформации линейно зависят от сил, потому участок I диаграммы называют участком пропорциональности. После точки В начинается так называемый участок текучести II.
На этой стадии стрелка силоизмерителя как бы спотыкается, приостанавливается, от точки В на диаграмме вычерчивается либо прямая, параллельная горизонтальной оси, либо слегка извилистая линия — деформации растут без увеличения нагрузки. Происходит перестройка структуры материала, устраняются нерегулярности в атомных решетках.
Далее самописец рисует участок самоупрочнения III. При дальнейшем увеличении нагрузки в образце происходят необратимые, большие деформации, в основном концентрирующиеся в зоне с макронарушениями в структуре – там образуется местное сужение — «шейка».
На участке IV фиксируется максимальная нагрузка, затем идет снижение усилия, ибо в зоне «шейки» сечение резко уменьшается, образец разрывается.
При нагружении на участке I в образце возникают только упругие деформации, при дальнейшем нагружении появляются и пластические — остаточные деформации.
Если в стадии самоупрочнения начать разгружать образец (например, от т. С), то самописец будет вычерчивать прямую СО1. На диаграмме фиксируются как упругие деформации Δlу (О1О2), так и остаточные Δlост (ОО1). Теперь образец будет обладать иными характеристиками.
Так, при новом нагружении этого образца будет вычерчиваться диаграмма О1CDЕ, и практически это будет уже другой материал. Эту операцию, называемую наклеп, широко используют, например, в арматурных цехах для улучшения свойств проволоки или арматурных стержней.
Диаграмма растяжения (рис. 1.2) характеризует поведение конкретного образца, но отнюдь не обобщенные свойства материала. Для получения характеристик материала строится условная диаграмма напряжений, на которой откладываются относительные величины – напряжения σ=F/A0 и относительные деформации ε=Δl/l0 (рис. 1.3), где А0, l0 – начальные параметры образца.
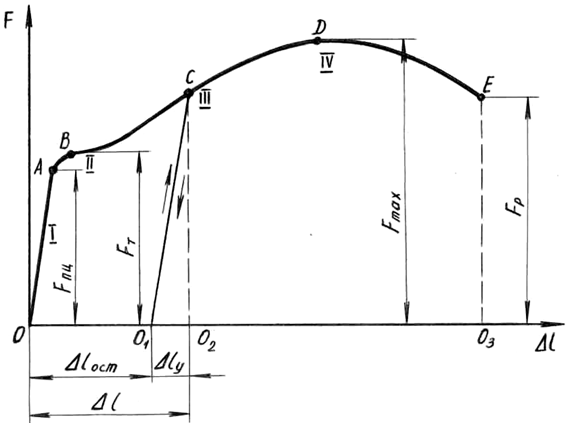
Рис. 1.2. Диаграмма растяжения образца из малоуглеродистой стали
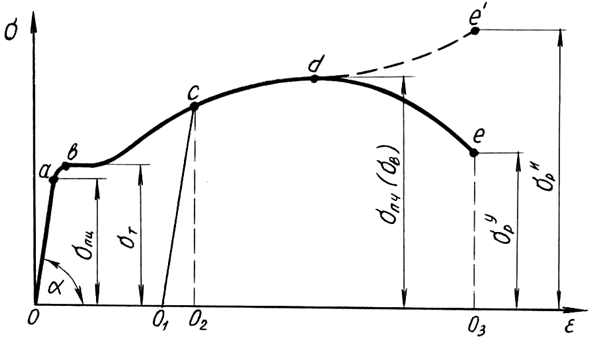
Рис. 1.3. Условная диаграмма напряжений при растяжении
Условная диаграмма напряжений при растяжении позволяет определить следующие характеристики материала (рис. 1.3):
σпц – предел пропорциональности – напряжение, превышение которого приводит к отклонению от закона Гука. После наклепа σпц может быть увеличен на 50-80%;
σу – предел упругости – напряжение, при котором остаточное удлинение достигает 0,05%. Напряжение σу очень близко к σпц и обнаруживается при более тонких испытаниях. В данной работе σу не устанавливается;
σт – предел текучести – напряжение, при котором происходит рост деформаций при постоянной нагрузке.
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют ≈0,2% (рис. 1.4);
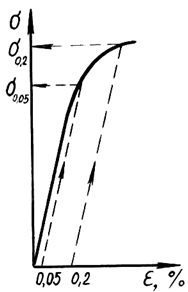
Рис. 1.4. Определение предела упругости и условного предела текучести
σпч (σв) – предел прочности (временное сопротивление) – напряжение, соответствующее максимальной нагрузке;
σр – напряжение разрыва. Определяется условное σур и истинное σир=Fр/Аш, где Аш – площадь сечения «шейки» в месте разрыва.
Определяются также характеристики пластичности – относительное остаточное удлинение
δ = (l1 – l0)∙100% / l0,
где l1 – расчетная длина образца после разрыва,
и относительное остаточное сужение
ψ = (А0 — Аш)∙100% / А0.
По диаграмме напряжений можно приближенно определить модуль упругости I рода
E=σпц/ε=tgα,
причем после операции наклепа σпц возрастает на 20-30%.
Работа, затраченная на разрушение образца W, графически изображается на рис. 1.2 площадью диаграммы OABDEO3. Приближенно эту площадь определяют по формуле:
W = 0,8∙Fmax∙Δlmax.
Удельная работа, затраченная на разрушение образца, говорит о мере сопротивляемости материала разрушению w = W/V, где V = A0∙l0 – объем рабочей части образца.
По полученным прочностным и деформационным характеристикам и справочным таблицам делается вывод по испытуемому материалу о соответствующей марке стали
Контрольные вопросы
- Изобразите диаграмму растяжения образца из малоуглеродистой стали (Ст.3). Покажите полные, упругие и остаточные абсолютные деформации при нагружении силой, большей, чем Fт.
- На каком участке образца происходят основные деформации удлинения? Как это наблюдается на образце? Какие нагрузки фиксируются в этот момент?
- Объясните, почему после образования шейки дальнейшее растяжение происходит при все уменьшающейся нагрузке?
- Перечислите механические характеристики, определяемые в результате испытаний материала на растяжение. Укажите характеристики прочности и пластичности.
- Дайте определение предела пропорциональности.
- Дайте определение предела упругости.
- Дайте определение предела текучести.
- Дайте определение предела прочности.
- Как определить предел текучести при отсутствии площадки текучести? Покажите, как это сделать, по конкретной диаграмме.
- Какие деформации называются упругими, какие остаточными? Укажите их на полученной в лабораторной работе диаграмме растяжения стали.
- Как определяется остаточная деформация после разрушения образца?
- Выделите на диаграмме растяжения образца из мягкой стали упругую часть его полного удлинения для момента действия максимальной силы.
- Какое явление называется наклепом? До какого предела можно довести предел пропорциональности материалов с помощью наклепа?
- Как определяется работа, затраченная на разрушение образца? О каком свойстве материала можно судить по удельной работе, затраченной на разрушение образца?
- Как определить марку стали и допускаемые напряжения для нее после проведения лабораторных испытаний?
- Чем отличается диаграмма истинных напряжений при растяжении от условной диаграммы?
- Можно ли определить модуль упругости материала по диаграмме напряжений?
- Как определить работу, затрачиваемую на деформации текучести лабораторного образца?
Испытание материалов на сжатие >
Краткая теория >
Примеры решения задач >
Источник
Макеты страниц
Рассмотрим теперь диаграмму зависимости между силой и деформацией в целом. В качестве наиболее типичного материала выберем мягкую сталь с небольшим содержанием углерода. Будем откладывать по оси ординат силу, поделенную на первоначальную площадь поперечного сечения, по оси абсцисс — удлинение, отнесенное к первоначальной длине. В результате получим диаграмму, изображенную на рис. 74.
Рис. 74.
Горизонтальный участок диаграммы называется участком текучести, а соответствующее напряжение — пределом текучести . В начале участка текучести на диаграмме часто появляется зуб, напряжение поднимается выше предела текучести, причем деформация приблизительно следует закону Гука, а потом падает до величины и сохраняет на площадке текучести постоянное значение. После того как достигнута точка В на диаграмме, нагрузка начинает возрастать, материал вновь приобретает способность сопротивляться пластической деформации. Это явление носит название упрочнения. До точки С на диаграмме удлинение происходит равномерно, первоначально цилиндрический образец сохраняет цилиндрическую форму, утоньшаясь с ростом удлинения. Достижение силой максимального значения в точке С связано с появлением шейки, то есть местного сужения образца. Начиная с этого момента, все растяжение локализируется в области шейки; сечение в середине шейки быстро уменьшается, настолько быстро, что, хотя напряжение продолжает расти, растягивающая сила убывает. Таким образом, падение диаграммы после точки С не означает, что способность материала сопротивляться деформации уменьшается, наоборот, сопротивление продолжает расти, но эффект уменьшения площади сечения оказывается преобладающим. Вне области шейки при уменьшении силы падают и напряжения, поэтому после достижения точки С значительная часть длины образца не подвергается дальнейшей деформации. Наконец, в точке D происходит разрыв образца. Сила, соответствующая точке С, называется разрушающей силой, частное от деления разрушающей силы на первоначальную площадь поперечного сечения называется временным сопротивлением или пределом прочности . Нужно заметить, что не есть напряжение, при котором происходит разрыв; для определения последнего следовало бы разделить силу, соответствующую точке D, на площадь сечения шейки в момент разрыва. Эта величина больше, чем временное сопротивление, но и ее нельзя принять за физическую характеристику прочности, так как в шейке напряженное состояние является сложным.
Временное сопротивление вообще не является напряжением, так как оно определяется по первоначальной площади сечения, а к моменту достижения точки С сечение образца успевает существенно уменьшиться. Таким образом, временное сопротивление — это условная характеристика, являющаяся суммарным выражением целого ряда физических свойств. Процесс образования шейки можно трактовать как процесс потери устойчивости равномерного течения металла, малые отклонения от идеальной геометрической формы до достижения точки временного сопротивления мало сказываются на процессе деформирования, тогда как после достижения этой точки эти малые случайные отклонения неизбежно растут и приводят к образованию шейки.
Временное сопротивление чрезвычайно просто определяется на опыте, для этого не нужно измерять деформации, достаточно разорвать образец на машине и отметить при этом максимальное достигнутое значение силы. Поэтому до настоящего времени эта характеристика является основной для суждения о прочности металла и до недавнего времени величины допускаемых напряжений устанавливались в зависимости от временного сопротивления.
Вторая важная характеристика — это относительное удлинение при разрыве, то есть абсцисса точки D. Важность этой характеристики уже была указана выше, в § 58. Высококачественные легированные стали тем и отличаются от простых углеродистых, что при высоком временном сопротивлении они обнаруживают большое удлинение при разрыве.
Строя диаграмму растяжения, подобную изображенной на рис. 74, мы не вправе называть величину, откладываемую по оси ординат, напряжением, так как площадь поперечного сечения образца меняется в процессе растяжения. Величина, откладываемая по оси абсцисс, также не может быть названа, строго говоря, относительным удлинением, так как после точки С все удлинение локализируется в области шейки и отнесение его к общей первоначальной длине образца теряет смысл. Истинной диаграммой растяжения, в отличие от приведенной на рис. 74 условной диаграммы, называется диаграмма зависимости между напряжением и относительной деформацией. Для построения такой диаграммы необходимо относить силу каждый раз к фактической площади поперечного сечения. До точки С построение истинной диаграммы не встречает принципиальных затруднений, удлинение определяется обычным способом, наряду с измерением деформации производится измерение поперечных размеров образца и производится соответствующий перерасчет. Истинная диаграмма, показанная на рис. 75, идет всегда выше условной, приведенной на том же чертеже пунктиром. В точке С, соответствующей точке С условной диаграммы, касательная к истинной диаграмме не становится горизонтальной, в соответствии с тем, что было сказано выше.
Для дальнейшего построения приходится прибегать к гипотезам, относящимся к распределению напряжений и деформаций в шейке; таким образом, часть истинной диаграммы после точки С получается не как результат прямого эксперимента, а на основе некоторого пересчета. Метод подобного пересчета предложил Н. Н. Давиденков.
Рис. 75.
Другая возможность построения диаграммы растяжения, связывающей не условные, а истинные (с известным приближением) напряжения и деформации, заключается в том, что по оси абсцисс откладывается не удлинение в направлении действия растягивающей силы, а поперечная деформация. За меру поперечной деформации принимают относительное уменьшение площади поперечного сечения образца:
Здесь — первоначальная площадь поперечного сечения образца, F — минимальная площадь поперечного сечения деформированного образца. Пока удлинение равномерно, величины связаны между собою следующим образом:
Это легко установить, воспользовавшись условием неизменности объема (изменение объема происходит только за счет упругой деформации, а ею можно пренебречь, когда удлинение велико).
Рис. 76.
Для большинства металлов диаграмма а — от точки С, соответствующей образованию шейки, почти до точки разрыва D (рис. 76) является прямолинейной. Диаграмма характеризует зависимость истинного напряжения от истинной деформации при растяжении лучше, чем условная диаграмма, но и она не отражает сложного характера напряженного состояния в шейке.
Источник
