Матрица растяжения и поворота
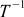
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 марта 2019;
проверки требуют 3 правки.
Ма́трицей поворо́та (или матрицей направляющих косинусов) называется ортогональная матрица[1], которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в двумерном пространстве[править | править код]
В двумерном пространстве поворот можно описать одним углом со следующей матрицей линейного преобразования в декартовой системе координат:
Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:
Координаты (x′,y′) в результате поворота точки (x, y) имеют вид:
Конкретные знаки в формулах зависят от того, является ли система координат правосторонней или левосторонней, и выполняется ли вращение по или против часовой стрелки. Верхний знак указан для обычного соглашения: правосторонняя система координат и положительное направление вращения против часовой стрелки (тот же знак верен для левосторонней координатной системы при выборе положительного направления вращения по часовой стрелке; в оставшихся двух комбинациях — нижний знак).
Матрица поворота в трёхмерном пространстве[править | править код]
Любое вращение в трёхмерном пространстве может быть представлено как композиция поворотов вокруг трёх ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трёх матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол в трёхмерном пространстве с неподвижной системой координат являются:
- Вращение вокруг оси :
- Вращение вокруг оси :
- Вращение вокруг оси :
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси[2]. Например, при повороте на угол вокруг оси ось переходит в : . Аналогично, и . Правая система координат связана с выбором правого базиса (см. правило буравчика).
Матрица поворота в -мерном пространстве[править | править код]
Совершенно аналогично могут быть записаны матрицы поворота конечномерного пространства любой более высокой размерности.
Надо только иметь в виду, что для размерностей пространства, не равных трём, невозможно указать единственную прямую, ортогональную двум данным прямым, а поэтому нельзя говорить о вращении вокруг какой-то оси, можно же говорить о вращении в какой-то плоскости[3]. Все точки при повороте в пространстве любой размерности, начиная с 2, всегда движутся параллельно некоторой (двумерной) плоскости.
Итак, совершенно аналогично трёхмерному случаю (с приведенной оговоркой) можем написать матрицу поворота в любой координатной плоскости для любой размерности пространства.
Например:
— матрица поворота в 5-мерном пространстве в плоскости ,
— матрица поворота в 7-мерном пространстве в плоскости .
- При таком подходе знаки перед синусами расставлять даже легче, поскольку они определяются порядком перечисления осей плоскости вращения: какая названа первой, в той строке перед синусом минус.
- Легко видеть, что матрица поворота в плоскости совпадает (что естественно) с матрицей поворота в плоскости и т. д. с точностью до замены угла поворота на противоположный.
- Поэтому такие матрицы с переставленными индексами очевидно не независимы, и для получения произвольного поворота достаточно включить в композицию каждую плоскость только один раз, то есть, скажем, только , а не и .
- Исходя из этого, нетрудно сосчитать их общее количество: , где n — размерность пространства.
Изменение оси поворота[править | править код]
Пусть — матрица поворота вокруг оси с ортом на угол , — матрица поворота вокруг оси с ортом на тот же угол, причем
где — матрица поворота, изменяющая орт оси поворота . Тогда
где — транспонированная матрица .
Перестановочность поворотов[править | править код]
Если — матрица поворота вокруг оси с ортом на угол , — матрица поворота вокруг оси с ортом на угол ,
то — матрица, описывающая поворот, являющийся результатом двух последовательно осуществленных поворотов ( и ), поскольку
При этом последовательность поворотов можно поменять, видоизменив поворот :
где матрица — матрица поворота на угол вокруг оси c ортом повернутым с помощью поворота :
поскольку , так как матрица поворота является ортогональной матрицей ( — единичная матрица). Заметим, что коммутативности поворотов в обычном смысле нет, то есть
Выражение матрицы поворота через углы Эйлера[править | править код]
Последовательные повороты около осей на угол прецессии (), угол нутации () и на угол собственного вращения () приводят к следующему выражению для матрицы поворота:
Ось — ось X, повёрнутая первым поворотом (на ), — ось Z, повёрнутая первым и вторым поворотом (на и ). Вследствие перестановочности поворотов приведённая матрица соответствует поворотам на углы , , вокруг осей Z, X, Z:
.
В случае, если повороты задаются в другой последовательности, матрица поворота находится перемножением матриц для вращения вокруг соответствующих декартовых осей координат, например:
Матрица поворота вокруг произвольной оси[править | править код]
Пусть ось вращения задана единичным вектором , а угол поворота .
Тогда матрица поворота в декартовых координатах имеет вид:
Выражение матрицы поворота через кватернион[править | править код]
Если задан кватернион , то соответствующая матрица поворота имеет вид:
Свойства матрицы поворота[править | править код]
Если — матрица, задающая поворот вокруг оси на угол , то:
Примечания[править | править код]
См. также[править | править код]
- Матрица перехода
- Поворот
Литература[править | править код]
- Лурье А. И. Аналитическая механика. — М.:Физматлит. — 1961. — 824 с.
Ссылки[править | править код]
- Поворот плоскости. Матрица поворота
Источник
В этой статье я кратко расскажу, как именно преобразуются координаты точек при повороте камеры в 3D играх, css-преобразованиях и вообще везде, где есть какие-то вращения камеры или предметов в пространстве. По совместительству это будет кратким введением в линейную алгебру: читатель узнает, что такое (на самом деле) вектор, скалярное произведение и, наконец, матрица поворота.
Введение
Задача. Предположим, что у нас есть двумерная картинка, как ниже (домик).
Предположим также, что мы смотрим на домик из начала координат в направлении ОХ. Теперь мы повернулись на некоторый угол против часовой стрелки. Вопрос: как будет выглядеть для нас домик? Интуитивно понятно, что результат будет примерно такой, как на картинке ниже.
Но как рассчитать результат? И, что хуже всего, как это делать в трехмерном пространстве? Если, например, мы вращаем камеру очень хитро: сначала вдоль оси ОZ, потом ОX, потом OY?
Ответы на эти вопросы даст статья ниже. Вначале я расскажу, как представлять домик в виде цифр (то есть расскажу о векторах), потом—о том, что такое углы между векторами (то есть о скалярном произведении) и наконец—о том, как вращать камеру (о матрице поворота).
Координаты вектора
Давайте подумаем о векторах. То есть о стрелках с длиной и направлением.
В приложении к компьютерной графике—каждая такая стрелка задает точку в пространстве.
Их-то мы и хотим научиться вращать. Потому что когда мы повернем все стрелки на картинке выше, мы повернем домик. Давайте представим, что все, что мы умеем делать с этими стрелками—это складывать и домножать на число. Как в школе: чтоб сложить два вектора, надо провести линию от начала первого вектора до конца второго.
Пока мы сосредоточимся на двумерных векторах. Для начала, нам хотелось бы научиться как-то записывать эти векторы через числа, потому что каждый раз рисовать их на бумаге в виде стрелок не очень удобно.
Научимся мы это делать, вспомнив о том, что любой вектор можно представить как сумму некоторых специальных векторов (ОХ и ОY), возможно, домноженных на определенные коэффициенты. Эти специальные векторы называются базисными, а коэффициенты—ни что иное, как координаты нашего вектора. Если мы будем обозначать базисные векторы через (здесь i—это индекс вектора, он равен либо 1, либо 2), рассматриваемый вектор как , а координаты последнего как , то получим формулу
(1)
Можно показать, что эти координаты будут единственными для данного базиса.
Польза от процедуры приписывания координат нашим стрелочкам очевидна—раньше надо было постоянно рисовать стрелку, чтоб описать вектор, а теперь достаточно просто написать два числа—координаты этого вектора. Например, мы можем условиться писать вот так: . Или так: . Тогда , а . Замечательно.
В настоящей математике процедура несколько другая. Вначале описываются свойства, которым должны удовлетворять какие угодно объекты, чтобы мы называли их векторами. Они очень естественные. Например, векторы должны поддерживать операцию сложения (двух векторов) и домножения на число. Сумма двух векторов не должна зависеть от порядка слагаемых. Сумма трех векторов не должна зависеть от того, в каком порядке мы их складываем попарно. И т. д. Полный список есть на википедии.
Если наши какие угодно штуки удовлетворяют этим свойствам, то эти штуки можно называть векторами (это такой duck typing). А все множество этих штук—векторным или линейным пространством. Свойства выше называют аксиомами, и из них выводят все остальные свойства векторов (или линейного пространства—отсюда и название «линейная алгебра»). Например, можно вывести, что среди векторов будут существовать такие особые, базисные векторы, через которые можно выразить любой вектор по формуле (1) и то, что это разложение на координаты будет единственным для данного базиса. Очень быстро можно показать, что наши стрелочки как раз удовлетворяют этим аксиомам. Аксиоматический подход удобен, потому что если мы столкнемся с какими-то другим объектами, которые удовлетворяют аксиомам, то к ним сразу можно применить все результаты нашей теории. Кроме того, так мы избегаем определений стрелочек на пальцах в начале теории.
Можно легко показать (из тех самых аксиом), что при сложении векторов их соответствующие координаты будут складываться, а при домножении вектора на число все координаты домножаются на это же число. Теперь, чтоб сложить два вектора, как на картинке ниже, мы можем не рисовать их (и не вести линию от начала первого вектора до конца второго), а писать, например, .
Скалярное произведение
Давайте теперь введем специальную функцию от двух произвольных векторов a и b, которую будем называть скалярным произведением. Мы будем обозначать его вот так: . Эти модные скобочки по-научному называются бра- и кет- векторы. Никакой пользы от них пока нет, но выглядит здорово—кроме того, это обозначение все-таки имеет глубокий смысл, особенно если вдаваться в математические подробности или квантовую механику.
В духе нашего аксиоматического подхода мы лишь потребуем, чтоб скалярное произведение удовлетворяло нескольким аксиомам. Если вместо первого вектора взять сумму векторов типа , то мы хотим, чтоб . Здесь греческие буквы—множители, x и y—вектора. Еще мы хотим, чтоб если такую сумму подставить вместо второго вектора, то можно сделать такие же преобразования (скалярное произведение суммы векторов тоже оказывается суммой скалярных произведений, а множители также выносятся за скобки). Кроме того, мы хотим, чтоб значения всегда были неотрицательными. Наконец, мы хотим, чтоб равнялось нулю тогда и только тогда, когда сам вектор нулевой. Ах да, и еще, чтоб .
Если мы добавим к наших стрелочкам на бумаге линейку и транспортир, то этим аксиомам будет удовлетворять функция, известная со школы: , где длины векторов меряются линейкой, угол между векторами —транспортиром.
Если же линейки и транспортира у нас нет, то из скалярного произведения можно определить длину вектора——и угол между векторами : . Конечно же, угол зависит от способа определения скалярного произведения.
Давайте посмотрим, как выражается скалярное произведение через отдельные координаты векторов. Предположим, что у нас есть два вектора a и b, которые выглядят вот так: , . Тогда .
Выглядит не очень. Чтоб сделать жизнь лучше, мы будем дальше работать только с особыми системами координат. Мы выберем только те системы координат, у которых базисные векторы имеют единичную длину и перпендикулярны между собой. Другими словами,
(2a) , если
(2b) , если
Такие векторы называются ортонормированными. Выражение для скалярного произведения в ортонормированных системах координат преображается до неузнаваемости:
(3)
Все системы координат в этой статье предполагаются ортонормированными. Удивительно, но из нашего построения следует, что результат формулы (3) не зависит от того, какой именно ортонормированный базис для координат выбрать.
Внимательно посмотрев на картинку «Разложение вектора на координаты» (она приведена еще раз после этого абзаца), можно заподозрить, что координата вектора—это не что иное, как его проекция на соответствующий базисный вектор. То есть значение скалярного произведения исходного вектора с одним из базисных векторов:
(4)
Действительно, например, . Кажется, что это тавтология, потому что координаты базисных векторов в своем же базисе всегда будут (1, 0) и (0, 1). Но ведь мы можем взять другие базисные векторы, и выразить их через старый базис. Например, новый ортонормированный базис может выглядеть в старом базисе как и . И тогда мы можем определить, например, первую координату вектора в новом базисе по формуле (4) как .
Дотошный читатель скажет «но ведь формулу (3) можно использовать в качестве определения скалярного произведения, и тогда нам не надо никакой ортонормированности базисных векторов». И будет прав в том, что формула (3) может работать как одно из определений скалярного произведения. Но здесь есть тонкий момент: тогда нам надо показать, что при изменении системы координат эта же формула, но с координатами векторов a и b из другого базиса, даст такое же число. А это будет только в том случае, если все базисы ортонормированны. Это можно будет показать, прочитав следующий раздел.
Поворот системы координат
Давайте выясним, как меняются координаты векторов, если мы меняем всю систему координат. Зачем нам вообще менять систему координат? Если немного подумать, то станет ясно, что поворот системы координат эквивалентен повороту камеры в 3D или 2D-моделировании (смотрите ниже чуть модифицированный рисунок с домиком). Так что научиться вращать систему координат—это как раз то, что нам надо.
Давайте обозначим i-ую координату вектора а в новой системе координат как , а новые базисные векторы как . Кроме того, обозначим j-ую координату СТАРОГО базисного вектора i в НОВОМ базисе как . Наконец, обозначим i-ую координату НОВОГО базисного вектора j в СТАРОМ базисе как . Теперь мы можем выразить исходный вектор и старые базисные векторы через новые базисные векторы. А именно
(5) и
(6)
Кроме того, можно выразить новые базисные векторы через старые:
(7)
Некоторые из этих разложений изображены на картинке ниже.
Теперь мы просто перепишем формулу (1) через векторы нового базиса:
Если сравнить это с формулой (5), и вспомнить, что координаты векторов определены однозначно, то можно заметить, что
(8) и
Удивительно, как эти формула похожи на уравнения (3)! Они выглядят как скалярное произведение вектора с определенными векторами (ниже мы покажем, что это не случайно).
Если записать уравнения (9) одной формулой, то получится
(9)
Эту формулу можно вывести по-другому, объединив (4), (1) и (7): . Если вспомнить свойства скалярного произведения, то эта формула распадается на четыре суммы. Если же теперь вспомнить о том, что наши базисные векторы ортонормированны, то получаем .
Эта формула выглядит не совсем так, как формула (9): вместо здесь стоят . Это не ошибка—просто . То есть j-ая координата СТАРОГО базисного вектора i в НОВОМ базисе всегда равна i-ой координате НОВОГО базисного вектора j в СТАРОМ базисе, . Это станет очевидно, если попытаться выразить эти координаты через формулу (4):
(10) ,
А скалярное произведение, как мы помним, не зависит от порядка произведения векторов.
Это станет еще более очевидно, если вспомнить о том, что эти скалярные произведения—это углы между разными (единичными) базисными векторами. Эти углы, разумеется, не зависят от того, откладывать ли их по или против часовой стрелки.
Матрица поворота
Если вы знакомы с матрицами, то формулу (9) (две формулы) можно переписать в матричном виде
(11)
Что это вообще все значит?! Как обычно, здесь нет никакой магии—просто мы договариваемся, что домножение этой таблички из чисел слева на вектор справа вычисляется как формула (9). То есть каждую строчку таблички мы домножаем на столбец справа (как будто бы мы совершаем скалярное произведение двух векторов), и результаты записываем друг под другом, тоже получая столбец.
Можно, кстати, распространить это правило на перемножение двух табличек: договоримся домножать каждую строчку первой таблички на каждый столбец второй, и результаты тоже записывать в табличку: перемножение первой строчки с третьим столбцом запишем в первую строчку и третий столбец. Формула (11) тогда становится частным случаем этого правила. Схематически это все изображено на рисунке ниже.
Таблички из чисел, снабженные таким правилом домножения на векторы и другие таблички, будем называть матрицами.
Правило перемножения матриц выглядит еще более естественно, если узнать, что скалярное произведение, как мы договорились его обозначать, , на самом предполагает, что вектор a—это строка, а вектор b—столбец. До этого мы договорились записывать векторы столбцами, и вектор-строка a на самом деле—это не просто перевернутый вектор a, а объект специального двойственного векторного пространства. Но в случае ортонормированных базисов координаты исходного и двойственного векторов совпадают (то есть а-строка и а-столбец одинаковы), так что эти детали не влияют на наше изложение. Все нормально. Кроме того, с другой стороны, формула (3) для скалярного произведения—это частный случай перемножения матриц.
Вообще, можно показать, что домножение на матрицы соответствует определенным трансформациям векторов. Вместо «трансформации» принято говорить операторы. А домножение на матрицу является линейным оператором. Кроме того, для любого линейного оператора существует одна и только одна матрица оператора. О том, что это такое, можно почитать на википедии. Если описывать это здесь, то статья никогда не закончится.
Итак, как мы выяснили, поворот системы координат эквивалентен повороту камеры в 3D или 2D-моделировании. Поэтому матрица из формулы (11) называется матрицей поворота. Формулу (11) можно интерпретировать не как замену системы координат, а как описание оператора поворота.
Пока не совсем понятно, как вычислять эту матрицу. Это несложно, если обратиться к формулам (10) и вспомнить, что косинус угла между единичными векторами равен их скалярному произведению. Тогда, например, , где —угол вращения системы координат (камеры). Он по определению положительный, если вращение происходит против часовой стрелки, и отрицательный при вращении по часовой стрелке (смотрите рисунок чуть ниже—он уже был, но теперь снова актуален). Если немного повозиться с геометрией или тригонометрией, то можно выяснить, что вся матрица поворота выглядит вот так:
(12a)
Если заглянуть в википедию, то формула там выглядит немного по-другому:
(12b)
Это все потому, что в ней—это угол вращения самих векторов (или наших объектов типа домика). Он тоже считается положительным, если вращение происходит против часовой стрелки. Но вращение камеры противоположно вращению объектов, то есть угол вращения камеры равен углу вращения объектов, но взятому с обратным знаком.
Снова актуальный рисунок:
Приятные мелочи
Эти матрицы—очень удобные штуки. Их можно перемножать и складывать, притом не только по две, но и по три и по четыре. Матрицы можно обозначать большими буквами. Например, Т—обычное обозначение для матриц поворота (она, безусловно, зависит от того, как поворачивать систему или камеру). Тогда формула (11) перейдет в .
У матриц есть единичная матрица—в том смысле, что любой вектор, будучи домноженным на нее слева, остается самим собой. И любая матрица тоже. Единичная матрица выглядит как таблица, вся заполненная нулями, только на диагонали стоят единицы. Такая матрица соответствует повороту на ноль градусов. То есть отсутствию поворота. Она выглядит так:
(13)
Если немного посчитать или подумать, то перемножение матриц поворота соответствует нескольким поворотам, совершенным один за другим (но в другом порядке—справа налево). Так что если в вашей программе происходит несколько заранее известных поворотов подряд, то не спешите их применять для всех точек в вашем трехмерном мире. Лучше перемножьте матрицы, получите общую матрицу поворота, и уже примените ее.
Для многих матриц можно найти такие, что при домножении первой на вторую получается единичная матрица. Эти новые матрицы называются обратными, и для T они обозначаются как . То есть .
Если еще немного подумать, то такая матрица должна соответствовать обратному для Т повороту—такому, который нейтрализует Т. Это уже очень удобно. Если научиться вычислять обратные матрицы, можно легко вращать камеру обратно, при необходимости.
Если подумать совсем не немного, и даже немного посчитать, то для матриц поворота, в силу того, что они обладают специальной структурой (см. формулу (10)), очень легко получить обратные матрицы: достаточно просто повернуть матрицу вдоль диагонали из левого верхнего в правый нижний угол (той самой диагонали, вдоль которой стоят единицы в единичной матрице). Эта операция называется транспонированием. Она намного (намного-намного) быстрее, чем поиск обратной матрицы в общем случае.
Трехмерное пространство
Наконец, перейдем к трехмерному пространству. Все формулы преобразуются тривиально—в векторах оказывается три координаты, в скалярном произведении—три суммы и т. п.
Сложность возникает только с матрицей поворота. Интуитивно почти очевидно, что любой поворот представим в виде последовательности трех поворотов (вдоль OX, OY, OZ) (впрочем, надо слегка потрудиться, чтоб это показать)—так что этими тремя углами поворота можно задать любое вращение. Три матрицы, соответствующие этим поворотам, можно перемножить, и получить общую матрицу для любого трехмерного поворота (с тремя параметрами—углами поворотов относительно координатных осей). Ее вид можно найти на википедии.
Можно показать, что вместо трех углов любой трехмерный поворот можно задать вектором, вокруг которого происходит поворот, и углом, на который мы вращаем камеру вдоль этого вектора (положим, против часовой стрелки, если смотреть с конца вектора). Как ни странно (а точнее, разумеется), этот способ тоже требует три числа. Поскольку длина вектора нам не важна, мы можем сделать его единичной длины. Тогда, чтоб его задать, нам потребуется только два числа (например, два угла—скажем, относительно OX и OY). К этим двум числам добавляется угол, на который мы будем совершать вращение относительно вектора. Формулу для матрицы поворота с этими параметрами тоже можно найти на википедии.
На этом все, спасибо за внимание.
P.S. В процессе подготовки статьи выяснилось, что формулы выглядят немного размытыми, хоть и сохранены вроде бы с 600 dpi в png. Видимо, так неудачно Inkscape сохраняет маленькие png. За это я дико извиняюсь, но сил переделывать у меня нет.
P.P.S. Хоть картинки и залиты на habrastorage, но иногда некоторые не отображаются. Видимо, какие-то проблемы с habrastorage. Попробуйте просто перезагрузите страничку
Источник
