Лекции по сопромату растяжение сжатие

Растяжение  (сжатие) – это такой   вид нагружения стержня, при котором в его поперечном сечении возникает внутренняя продольная сила Ν, действующая вдоль центральной оси z.

Продольная сила Ν – это равнодействующая всех внутренних нормальных сил в сечении. Для вычисления продольной силы применяется метод сечений.

Продольная сила Ν численно равна алгебраической сумме проекций всех сил, действующих по одну сторону от рассматриваемого сечения,  на продольную ось бруса.

Правило знаков для продольной силы Ν: при растяжении продольная сила положительна, при сжатии – отрицательна.

График изменения продольных сил по длине стержня называется эпюрой. Эпюра N строится методом сечений на характерных участках бруса. Строится эпюра для использования ее при расчете бруса на прочность. Она дает возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.

При растяжении (сжатии) возникают только нормальные напряжения. Согласно гипотезе Я. Бернулли (или гипотеза плоских сечений) в поперечных сечениях, удаленных от места приложения нагрузок, нормальные напряжения распределяются по сечению практически равномерно, а сами сечения, перпендикулярные к оси стержня z, остаются плоскими в процессе нагружения.

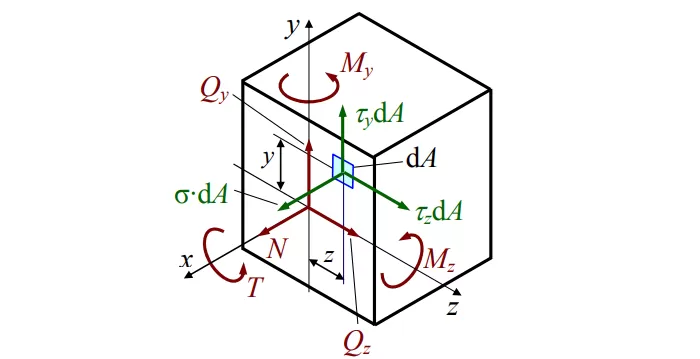
Нормальные напряжения в сечении при  растяжении (сжатии) вычисляются по формуле

где А – площадь поперечного сечения.

Правило знаков для σ совпадает с правилом знаков для N.

В наклонном сечении, нормаль к которому составляет угол α с осью стержня z,

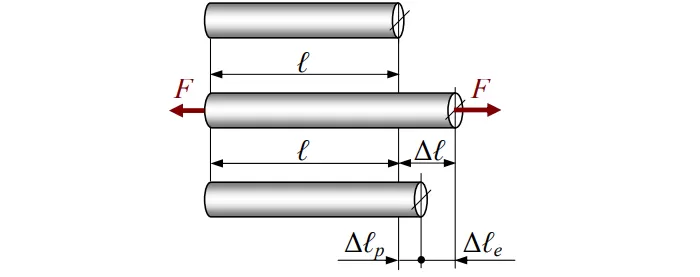
При растяжении в продольном направлении стержень удлиняется, а его поперечные размеры уменьшаются, при сжатии, напротив, в продольном направлении стержень укорачивается, а его поперечные размеры увеличиваются; Δℓ — абсолютное удлинение или укорочение участка стержня длиной ℓ, Δb – абсолютная поперечная деформация.

Относительное удлинение или укорочение участка стержня длиной ℓ, называемое линейной деформацией, определяется следующим образом

ε=Δℓ/ℓ.

Экспериментально установлено, что в определенной области нагрузок при упругом поведении материала между нормальными напряжениями и линейными деформациями существует линейная зависимость (закон Гука для напряжений)

σ=εЕ,

где Е – модуль продольной упругости или модуль Юнга, это физическая const. Для каждого из материалов величина модуля упругости имеет свое значение:

сталь, Е = 2.105 МПа,

медь, Е = 1.105 МПа,

алюминий, Е = 0,7.105 МПа.

Значение модуля упругости устанавливается экспериментально.

Согласно закону Гука (данную запись называют законом Гука для деформаций)

Δℓ=Νℓ/ЕА

Произведение ЕА – называется жесткостью стержня при растяжении – сжатии.

Перемещение произвольного сечения ступенчатого стержня

w=∑Δℓi

Относительная поперечная деформация:

ε′=Δb/b

где b – поперечный размер стержня.

Эксперименты также показывают, что в упругой стадии деформирования между продольной и поперечной деформациями существует взаимосвязь

μ  =│ε′⁄ε│ — const,

где   μ —  коэффициент Пуассона, берется по модулю ,поскольку у продольной и поперечной деформации разные знаки (при растяжении продольные волокна увеличиваются, а поперечные уменьшаются в размере).

Для твердых материалов имеет значения коэффициент Пуассона

0≤μ ≤0,5

Изменение температуры стержня вызывает его удлинение (при нагревании) или укорочение (при охлаждении)

где — a- коэффициент линейного температурного расширения; Δtº=(tºк-tºн) — изменение температуры между значениями начальным (tºн) и конечным (tºк).

Статически неопределимыми называют системы, имеющие лишние связи – внешние или внутренние.

Для определения внутренних усилий в таких системах недостаточно рассматривать только уравнения равновесия.

В этом случае требуются дополнительные уравнения, число которых равно количеству лишних связей. Дополнительные уравнения составляются на основе анализа картины деформирования системы и использования законов деформирования ее элементов.

Алгоритм решения подобных задач включает следующее:

1)   Статическая часть. Составляются уравнения равновесия с включением неизвестных усилий, действующих по направлению лишних связей.

2)    Геометрическая часть. Составляются уравнения, описывающие взаимосвязь перемещений характерных точек, удлинений и укорочений отдельных стержней между собой.

3)   Физическая связь. Записываются законы деформирования отдельных стержней системы.

Порядок расчета статически неопределимых брусьев

1.  Задаться направлениями возможных опорных реакций и составить уравнение      статики для всей системы в целом.
2. Определить степень статической неопределимости и использовать метод сечений с целью выразить неизвестные усилия через неизвестные опорные реакции. При этом неизвестные продольные силы (N) следует предполагать положительными и поэтому направлять «от сечения».
3. Сформулировать условие совместности деформаций участков бруса.
4. В процессе превращения условия совместности в уравнение совместности деформаций различий в характере деформаций участков не учитывать.

Порядок расчета статически неопределимых шарнирно-стержневых систем

1. Задаться направлениями опорных реакций, но уравнений равновесия для всей системы не составлять, а сразу использовать метод сечений и составить уравнения статики для выделенной части системы.
2. Определить степень статической неопределимости как разницу между количеством всех неизвестных, оказавшихся в уравнениях статики, и числом самих этих уравнений.
3. Рассмотреть (изобразить) любую возможную картину деформаций системы и из ее анализа сформулировать условия совместности деформаций стержней системы (столько, какова степень статической неопределимости).
4. В процессе преобразования условий совместности в уравнения совместности деформаций обязательно учитывать различие в характере деформаций стержней (т.е. вводить удлинение со знаком «плюс», а укорочение со знаком «минус») в соответствии с той картиной деформации, которую мы рассматриваем.

Многочисленные учебники «Cопромат для чайников» создают для развенчания мифа о непостижимой сложности дисциплины. Этой наукой пугают на первых курсах вузов. Для начала расшифруем грозный термин «сопротивление материалов».

На деле – проста и решение почти не выходит за рамки школьной задачи о растяжении и сжатии пружины. Другое дело – найти слабое звено конструкции и свести расчет к несложной постановке. Так что не стоит зевать на лекциях по основам механики. При подготовке к урокам можно пользоваться решениями онлайн, но на экзаменах помогут только свои знания.

Что такое сопромат

Это методика расчета деталей, конструкций на способность выдерживать нагрузки в требуемой степени. Или хотя бы для предсказания последствий. Не более, хотя почему-то относят руководство к наукам.

Этой «наукой» прекрасно владели древнегреческие и древнеримские инженеры, сооружавшие сложнейшие механизмы. Понятия не имея о структуре, уравнении состояния вещества и прочих теориях, египтяне строили исполинские плотины и пирамиды.

Основные задачи по сопротивлению материалов

Задача следует напрямую из определения. А вот каковы критерии упомянутого слова «выдерживать»? Неясно, что скрывается под «материалом» и как реальные вещи схематизировать.

Требования

Перечислены далеко не все, но для статики и базовой программы хватит:

1. Прочность – способность образца воспринимать внешние силы без разрушения. Слегка мнущаяся под весом оборудования подставка никого не интересует. Основную-то функцию она выполняет.

2. Жесткость – свойство воспринимать нагрузку без существенного нарушения геометрии. Гнущийся под силой резания инструмент даст дополнительную погрешность обработки. К ошибке приведет деформация станины агрегата.

3. Устойчивость – способность конструкции сохранять стабильность равновесия. Поясним на примере: стержень находится под грузом, будучи прямым – выдерживает, а чуть изогнется – характер напряжения изменится, груз рухнет.

Материал и силы

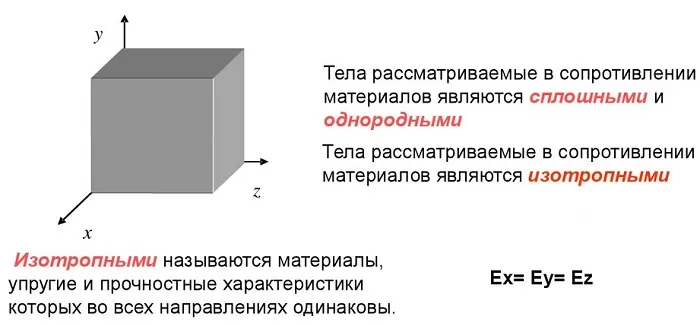
Как всякая методика, сопромат принимает массу упрощений и прямо неверных допущений:

• материал однороден, среда сплошная. Внутренние особенности в расчет не берутся;

• свойства не зависят от направления;

• образец восстанавливает начальные параметры при снятии нагрузки;

• поперечные сечения не меняются при деформации;

• в удаленных от места нагрузки местах усилие распределяется равно по сечению;

• результат воздействия нагрузок равен сумме последствий от каждой;

• деформации не влияют на точки приложения сил;

• отсутствуют изначальные внутренние напряжения.

Схемы

Служат для создания возможности расчета реальных конструкций:

• тело – объект с практически одинаковыми «длина х ширина х высота»;

• брус (балка, стержень, вал) – характеризуется значительной длиной.

На рисунке показаны опоры с воспринимаемыми реакциями (обозначены красным цветом):

Рис. 1. Опоры с воспринимаемыми реакциями:

а) шарнирно-подвижная;

б) шарнирно-неподвижная;

в) жесткая заделка (защемление).

Силы в сопромате

Приложенные извне, уравновешиваются возникающими изнутри. Напомним, рассматривается статическая ситуация. Материал «сопротивляется».

Разделим нагруженное тело виртуальным сечением P (см. рис. 2).

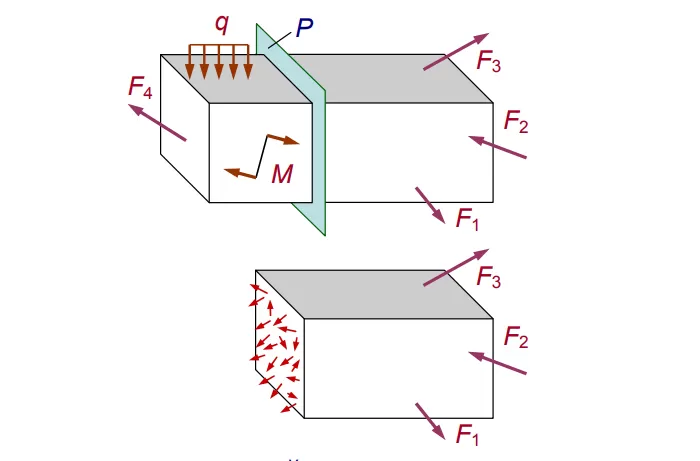
Рис. 2

Заменим хаос равнодействующей R и моментом M (см. рис. 3):

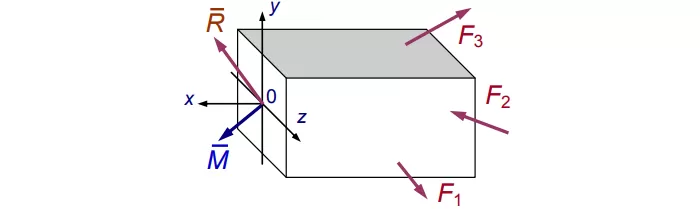
Рис. 3

Распределив по осям, получим картину нагрузки сечения (см. рис. 4):

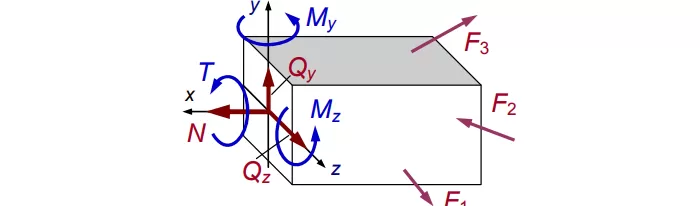
Рис. 4

Нагрузки и деформации, изучаемые в сопромате

Изучим несколько принятых терминов.

Напряжения

В теле приложенные силы распределяются по сечению. Нагружен каждый элементарный «кусочек». Разложим силы:

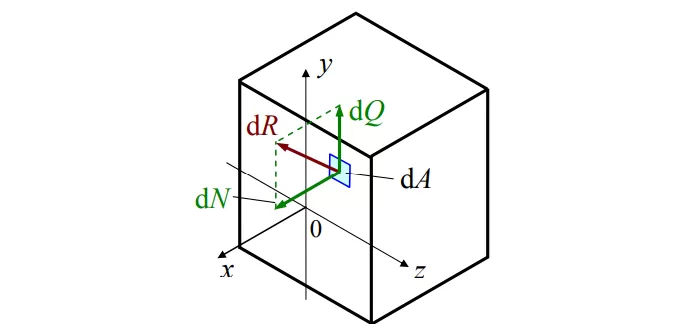
Элементарные усилия таковы:

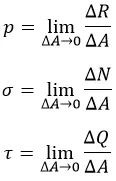
• σ – «сигма», нормальное напряжение. Перпендикулярно сечению. Характерно для сжатия / растяжения;

• τ – «тау», касательное напряжение. Параллельно сечению. Появляется при кручении;

• p – полное напряжение.

Просуммировав элементы, получим:

Здесь:

• N – нормальная сила;

• A – площадь сечения.

В принятой в России системе СИ сила измеряется в ньютонах (Н). Напряжения – в паскалях (Па). Длины в метрах (м).

Деформации

Различают деформацию упругую (с индексом «e») и пластическую (с индексом «p»). Первая исчезает по снятии растягивающей / сжимающей силы, вторая – нет. 

Полная деформация будет равна:

Деформация относительная обозначается «ε» и рассчитывается так:

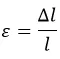
Под «сдвигом» понимается смещение параллельных слоев. Рассмотрим рисунок:

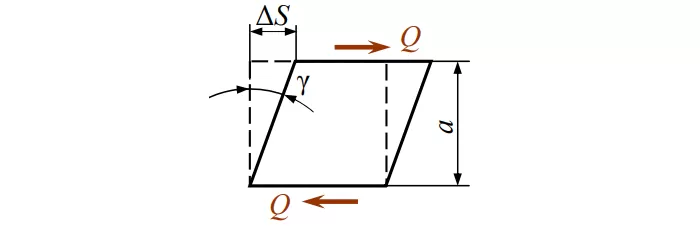
Здесь γ – относительный сдвиг.

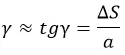
Виды нагрузки

Перечислены основные.

1. Растяжение и сжатие – нагрузка нормальной силой (по оси стержня).

2. Кручение – действует момент. Обычно рассчитываются передающие усилия валы.

3. Изгиб – воздействие направлено на искривление.

Основные формулы

Базовый принцип сопромата единственный. В упомянутой задаче о пружине применим закон Гука:

E – модуль упругости (Юнга). Величина зависит от используемого материала. Для стали полагают равным 200 х 106 Па.

Сопротивление материала прямо пропорционально деформации:

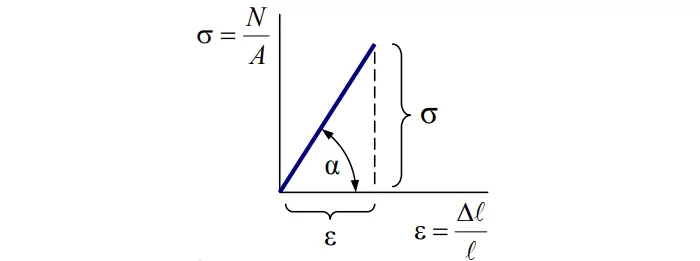
Закон верен не всегда и не для всех материалов. Как уже упоминалось, принимается как одно из допущений.

Реальная диаграмма

Растяжение стержня из низкоуглеродистой стали выглядит следующим образом:

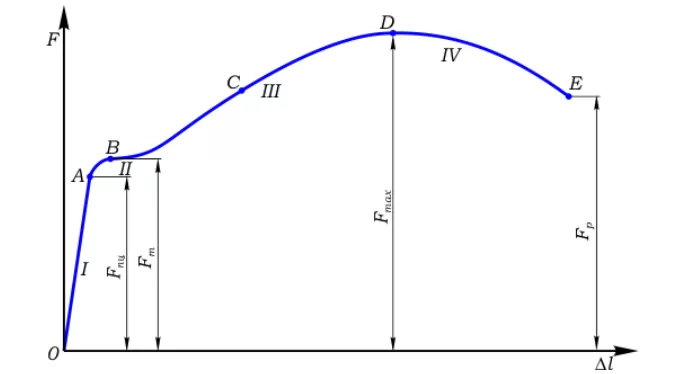
Принимаемые схемы:

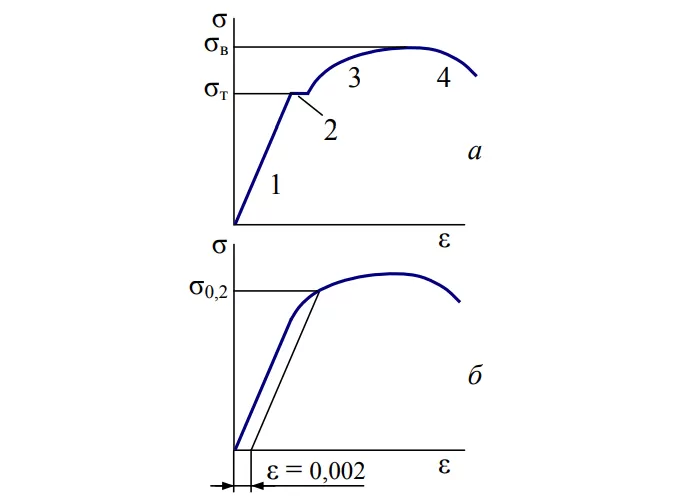
График (б) относится к большей части конструкционных материалов: подкаленные стали, сплавы цветных металлов, пластики.

Расчеты обычно ведут по σт (а) и σ0.2 (б). С незначительными пластическими деформациями конструкции или без таковых.

Пример решения задачи

Какой груз допустимо подвесить на пруток из стали 45 Ø10 мм?

Решение.

σ0,2 для стали 45 равна 245 МПа (из ГОСТ).

Площадь сечения прутка:

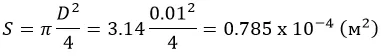
Допустимая сила тяжести:

Для получения веса следует разделить на ускорение свободного падения g:

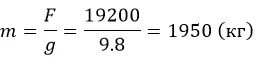
Ответ: необходимо подвесить груз массой 1950 кг.

Как найти опасное сечение

Наиболее простой способ – построение эпюры. На закрепленную балку действуют точечные и распределенные силы. Считаем на характерных участках, начиная с незакрепленного конца. 

Усилие положительно, если направлено на растяжение.

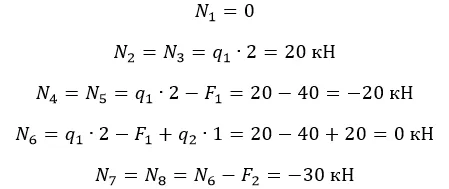
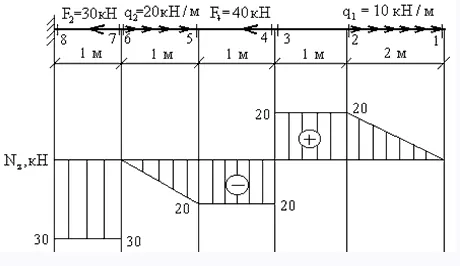
На схеме показано, что:

• на участке (7 — 8) действует сжатие 30 кН;

• на (2 — 3) – растяжение 20 кН.

Зачем и кому нужен сопромат

Даже не имеющий отношения к прочностным расчетам инженер-универсал должен иметь понятие о приблизительных (на 10-20%) значениях. Знать конструкционные материалы, представлять свойства. Чувствовать заранее слабые места агрегатов.

Совершенно необходим разработчикам различных конструкций, машиностроительных изделий. Будущим архитекторам в вузах преподается в виде предмета «Строительная механика».

Методика помогает на стадии проектирования обеспечивать необходимый запас прочности изделий. Стойкость к постоянным и динамичным нагрузкам. Это сберегает массу времени и затрат в дальнейших изготовлении, испытании и эксплуатации изделия. Обеспечивает надежность и долговечность.