Лабораторные работы по сопромату растяжение
Лабораторная работа № 1
Цель работы – изучить поведение малоуглеродистой стали при растяжении и определить ее механические характеристики.
Основные сведения
Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.
Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.
В таких случаях, кроме металлографических исследований, определяются главные механические характеристики на образцах, взятых из зоны разрушения конструкции. Образцы изготавливаются по ГОСТ 1497-84 и могут иметь различные размеры и форму (рис. 1.1).
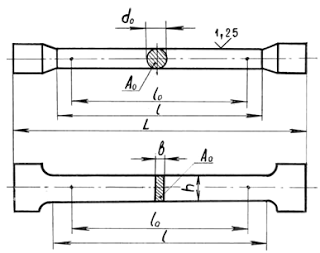
Рис. 1.1. Образцы для испытания на растяжение
Между расчетной длиной образца lо и размерами поперечного сечения Ао (или dо для круглых образцов) выдерживается определенное соотношение:
В испытательных машинах усилие создается либо вручную — механическим приводом, либо гидравлическим приводом, что присуще машинам с большей мощностью.
В данной работе используется универсальная испытательная машина УММ-20 с гидравлическим приводом и максимальным усилием 200 кН, либо учебная универсальная испытательная машина МИ-40КУ (усилие до 40 кН).
Порядок выполнения и обработка результатов
Образец, устанавливаемый в захватах машины, после включения насоса, создающего давление в рабочем цилиндре, будет испытывать деформацию растяжения. В измерительном блоке машины есть шкала с рабочей стрелкой, по которой мы наблюдаем рост передаваемого усилия F.
Зависимость удлинения рабочей части образца от действия растягивающей силы во время испытания отображается на миллиметровке диаграммного аппарата в осях F-Δl (рис. 1.2).
В начале нагружения деформации линейно зависят от сил, потому участок I диаграммы называют участком пропорциональности. После точки В начинается так называемый участок текучести II.
На этой стадии стрелка силоизмерителя как бы спотыкается, приостанавливается, от точки В на диаграмме вычерчивается либо прямая, параллельная горизонтальной оси, либо слегка извилистая линия — деформации растут без увеличения нагрузки. Происходит перестройка структуры материала, устраняются нерегулярности в атомных решетках.
Далее самописец рисует участок самоупрочнения III. При дальнейшем увеличении нагрузки в образце происходят необратимые, большие деформации, в основном концентрирующиеся в зоне с макронарушениями в структуре – там образуется местное сужение — «шейка».
На участке IV фиксируется максимальная нагрузка, затем идет снижение усилия, ибо в зоне «шейки» сечение резко уменьшается, образец разрывается.
При нагружении на участке I в образце возникают только упругие деформации, при дальнейшем нагружении появляются и пластические — остаточные деформации.
Если в стадии самоупрочнения начать разгружать образец (например, от т. С), то самописец будет вычерчивать прямую СО1. На диаграмме фиксируются как упругие деформации Δlу (О1О2), так и остаточные Δlост (ОО1). Теперь образец будет обладать иными характеристиками.
Так, при новом нагружении этого образца будет вычерчиваться диаграмма О1CDЕ, и практически это будет уже другой материал. Эту операцию, называемую наклеп, широко используют, например, в арматурных цехах для улучшения свойств проволоки или арматурных стержней.
Диаграмма растяжения (рис. 1.2) характеризует поведение конкретного образца, но отнюдь не обобщенные свойства материала. Для получения характеристик материала строится условная диаграмма напряжений, на которой откладываются относительные величины – напряжения σ=F/A0 и относительные деформации ε=Δl/l0 (рис. 1.3), где А0, l0 – начальные параметры образца.
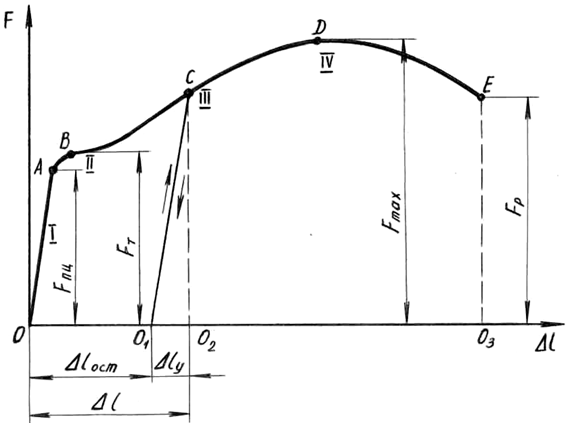
Рис. 1.2. Диаграмма растяжения образца из малоуглеродистой стали
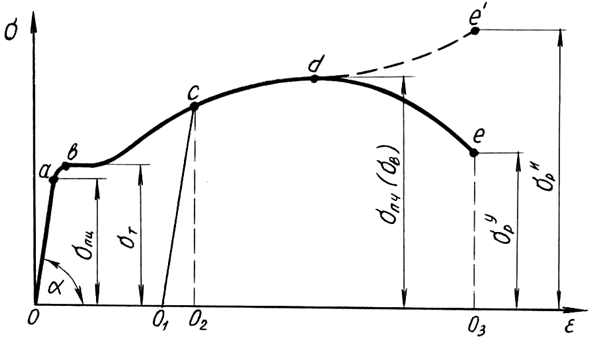
Рис. 1.3. Условная диаграмма напряжений при растяжении
Условная диаграмма напряжений при растяжении позволяет определить следующие характеристики материала (рис. 1.3):
σпц – предел пропорциональности – напряжение, превышение которого приводит к отклонению от закона Гука. После наклепа σпц может быть увеличен на 50-80%;
σу – предел упругости – напряжение, при котором остаточное удлинение достигает 0,05%. Напряжение σу очень близко к σпц и обнаруживается при более тонких испытаниях. В данной работе σу не устанавливается;
σт – предел текучести – напряжение, при котором происходит рост деформаций при постоянной нагрузке.
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют ≈0,2% (рис. 1.4);

Рис. 1.4. Определение предела упругости и условного предела текучести
σпч (σв) – предел прочности (временное сопротивление) – напряжение, соответствующее максимальной нагрузке;
σр – напряжение разрыва. Определяется условное σур и истинное σир=Fр/Аш, где Аш – площадь сечения «шейки» в месте разрыва.
Определяются также характеристики пластичности – относительное остаточное удлинение
δ = (l1 – l0)∙100% / l0,
где l1 – расчетная длина образца после разрыва,
и относительное остаточное сужение
ψ = (А0 — Аш)∙100% / А0.
По диаграмме напряжений можно приближенно определить модуль упругости I рода
E=σпц/ε=tgα,
причем после операции наклепа σпц возрастает на 20-30%.
Работа, затраченная на разрушение образца W, графически изображается на рис. 1.2 площадью диаграммы OABDEO3. Приближенно эту площадь определяют по формуле:
W = 0,8∙Fmax∙Δlmax.
Удельная работа, затраченная на разрушение образца, говорит о мере сопротивляемости материала разрушению w = W/V, где V = A0∙l0 – объем рабочей части образца.
По полученным прочностным и деформационным характеристикам и справочным таблицам делается вывод по испытуемому материалу о соответствующей марке стали
Контрольные вопросы
- Изобразите диаграмму растяжения образца из малоуглеродистой стали (Ст.3). Покажите полные, упругие и остаточные абсолютные деформации при нагружении силой, большей, чем Fт.
- На каком участке образца происходят основные деформации удлинения? Как это наблюдается на образце? Какие нагрузки фиксируются в этот момент?
- Объясните, почему после образования шейки дальнейшее растяжение происходит при все уменьшающейся нагрузке?
- Перечислите механические характеристики, определяемые в результате испытаний материала на растяжение. Укажите характеристики прочности и пластичности.
- Дайте определение предела пропорциональности.
- Дайте определение предела упругости.
- Дайте определение предела текучести.
- Дайте определение предела прочности.
- Как определить предел текучести при отсутствии площадки текучести? Покажите, как это сделать, по конкретной диаграмме.
- Какие деформации называются упругими, какие остаточными? Укажите их на полученной в лабораторной работе диаграмме растяжения стали.
- Как определяется остаточная деформация после разрушения образца?
- Выделите на диаграмме растяжения образца из мягкой стали упругую часть его полного удлинения для момента действия максимальной силы.
- Какое явление называется наклепом? До какого предела можно довести предел пропорциональности материалов с помощью наклепа?
- Как определяется работа, затраченная на разрушение образца? О каком свойстве материала можно судить по удельной работе, затраченной на разрушение образца?
- Как определить марку стали и допускаемые напряжения для нее после проведения лабораторных испытаний?
- Чем отличается диаграмма истинных напряжений при растяжении от условной диаграммы?
- Можно ли определить модуль упругости материала по диаграмме напряжений?
- Как определить работу, затрачиваемую на деформации текучести лабораторного образца?
Испытание материалов на сжатие >
Краткая теория >
Примеры решения задач >
Источник
ЛАБОРАТОРНЫЕ РАБОТЫ ПО СОПРОМАТУ, ЧАСТЬ 1
Работы №1,2,3,4,5,6
1. Механические характеристики материалов, используемые при расчетах на прочность, определяются экспериментально на стандартных образцах.
2. Основными являются испытания на растяжение, сжатие, кручение. В результате испытаний получается кривая в координатах нагрузка – перемещение, называемая характеристикой образца.
3. диаграммой или характеристикой материала — кривая, построенная в координатах напряжение – деформация, С помощью определенных формул
Лабораторная работа №1
ИСПЫТАНИЕ НА РАСТЯЖЕНИЕ ОБРАЗЦОВ МАТЕРИАЛА
Для испытаний на растяжение используется десятикратный образец (рис.1.1 в журнале), у которого l0 = 10 d0. Здесь l0 — длина базы, т.е. размера, изменения которого фиксируются при эксперименте как Δl – удлинение образца, d0 – первоначальный диаметр образца. Образец растягивают до тех пор, пока он не разрушится. После испытаний получается характеристика образца в координатах F, Δl. С помощью формул и из характеристики образца получается диаграмма (характеристика) материала в координатах — напряжение, — деформация.
Испытание малоуглеродистой стали — типичного пластичного материала
Участки характеристики образца:
ОА — линейный участок, материал подчиняется закону Гука, удлинение образца определяется по формуле ; до точки В деформации упруги, то есть они полностью исчезают после разгрузки;
CD — горизонтальный участок диаграммы — площадка текучести, деформации интенсивно нарастают при постоянной нагрузке;
DE — зона упрочнения: в кристаллах металла произошла перестройка, и материал может снова сопротивляться нагружению;
EG — зона разрушения.
В точке Е при в образце возникает местное утонение — шейка. Дальнейшие деформации сосредотачиваются в районе шейки, которая при этом интенсивно утоняется, деформировать образец становится легче и поэтому нагрузка уменьшается. После разрыва образца материал в районе шейки теплый. Это зона больших пластических деформаций, при их образовании материал нагревается.
На характеристике образца с помощью геометрических построений находят характерные точки, соответствующие силам Fпц, Fy, Fт, Fmax, Fраз. Затем по формулам сопромата вычисляют соответствующие напряжения и строят диаграмму (характеристику) материала, с помощью которойопределяют механические характеристики материала:
— предел пропорциональности — наибольшее напряжение, до которого справедлив закон Гука (s = E e);
— предел упругости — наибольшее напряжение, до которого деформации полностью упруги, то есть целиком исчезают при разгрузке;
— предел текучести — напряжение, при котором деформации интенсивно нарастают при постоянной нагрузке;
— предел прочности — напряжение, численно равное максимальной нагрузке, деленной на первоначальную площадь сечения образца.
Характеристика стали называется условной, так как она получена на основании формул и , где A0 и l0 — первоначальная площадь сечения и первоначальная длина образца, в то время как при растяжении изменяются как длина образца, так и размеры его сечения. Если учитывать эти изменения, то получим истинную диаграмму, изображенную тонкой линией на рис. 1.12. Только на истинной диаграмме есть напряжение при разрыве , это самое большое значение напряжения во время испытаний. Amin — площадь сечения шейки в месте разрыва, , dmin — диаметр шейки в месте разрыва. При растяжении стальной образец интенсивно деформируется. Остаточное удлинение после разрыва достигает 30%.
Образец после разрыва
На условной характеристике напряжения при разрыве нет!
В конструкциях, как правило, материал работает при напряжениях, меньших предела текучести. Как видно из рис. 1.12, условная и истинная диаграммы практически совпадают и до значения напряжения, равного пределу текучести sт. Поэтому на практике используют для расчетов условную диаграмму.
Если материал нагрузить за пределы упругости и разгрузить, то при разгрузке исчезнут только упругие деформации, а пластические останутся (рис. 1.14).
Закон разгрузки и повторного нагружения
Если нагрузить материал за пределы упругой зоны (точка К выше точки В, соответствующей пределу упругости, рис. 1.14), а затем разгрузить, то линия разгрузки KL будет параллельна первоначальному участку диаграммы ОА (точка А соответствует пределу пропорциональности). При вторичном нагружении (линия LK) материал сохраняет пропорциональную зависимость между нагрузкой F и удлинением Dl (то есть между s и e) вплоть до максимального напряжения первичного нагружения (точка K), а затем следует по первоначальной кривой КЕ. Это свойство материалов используется на практике, например, при заневоливании пружин. После изготовления пружины нагружают за пределы упругости, увеличивая тем самым величину осадки пружины, пропорциональную силе.
На рис. 1.14:
OАВK — линия первичного нагружения;
KL — линия разгрузки;
OL — пластическое или остаточное удлинение образца;
LM — упругое удлинение, исчезающее при разгрузке;
LKE — линия вторичного нагружения.
Таким образом, удлинение образца в точке K (отрезок ОM на рис. 1.14) с помощью линии разгрузки KL,параллельной первоначальному линейному участкудиаграммы ОА, можно разделить на упругую часть (LM) и пластическую часть (OL).
Условный или технический предел текучести
Некоторые пластичные материалы, например, алюминий, не имеют площадки текучести на диаграмме. Для таких материалов используется условный или технический предел текучести
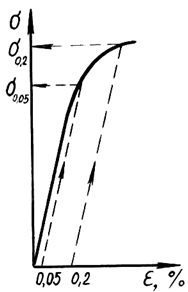
s0,2 — это напряжение, при котором остаточная деформация равна 0,2%, то есть величина 0,002 в масштабе диаграммы, рис. 1.15.
Для определения s0,2 сначала отложим по оси e величину остаточной деформации, равную 0,002 в масштабе диаграммы. Затем проведем LK÷÷ ОА. Получим пересечение с кривой (точка K). Соответствующее точке K напряжение и есть условный или технический предел текучести s0,2.
Лабораторная работа №2
ИСПЫТАНИЕ НА СЖАТИЕ ОБРАЗЦОВ МАТЕРИАЛА
Для испытаний на сжатие используется цилиндрический образец, , рис. 2.11.
Испытание чугуна
— предел прочности чугуна при сжатии.
Чугун при сжатии разрушается по поверхностям, наклоненным примерно под углом 45° к оси образца, рис. 2.14. Именно в этих плоскостях действуют максимальные касательные напряжения при растяжении, сжатии, и чугун разрушается от сдвигов в кристаллической решетке по этим плоскостям.
Чугун работает на сжатие лучше, чем на растяжение, предел прочности чугуна при сжатии больше предела прочности при растяжении , рис. 2.15.
На рис. 2.16 приведены характеристики стали и чугуна при сжатии.
Предел текучести стали при сжатии меньше предела прочности чугуна при сжатии .
Лабораторная работа №3
ИСПЫТАНИЕ НА КРУЧЕНИЕ ОБРАЗЦОВ МАТЕРИАЛА
Для испытания материалов при чистом сдвиге (при кручении) используют цилиндрический образец. В процессе испытаний записывается диаграмма кручения — зависимость M = f(j). М — это нагрузка, то есть момент, скручивающий образец, j — угол закручивания образца, рис. 3.11
(рис. 3.1 в журнале).
Лабораторная работа № 4
ОПРЕДЕЛЕНИЕ УПРУГИХ ПОСТОЯННЫХ ИЗОТРОПНЫХ МАТЕРИАЛОВ
Коэффициентом Пуассона ν называется модуль отношения поперечной относительной деформации к продольной: . Для всех материалов коэффициент Пуассона изменяется в пределах ( ν = 0 для пробки и ν = 0,5 для резины).
Модулем упругости первого рода или модулем Юнганазывается коэффициент пропорциональности между напряжениями и деформациями в начальной стадии нагружения материала или коэффициент пропорциональности в законе Гука. Этот коэффициент характеризует неподатливость материала к деформациям.
Для экспериментального определения коэффициента Пуассона надо замерить поперечную и продольную деформации в растянутом плоском образце (рис. 4.2 в журнале).
Деформация измеряется электрическим тензометром, который состоит из датчика омического сопротивления, или тензорезистора, и электронного усилителя деформации, который представляет собой мостик Уитстона, рис. 4.11 (рис.4.4 в журнале).
Мостик это четыре сопротивления как четыре стороны квадрата. Одна диагональ этого квадрата – источник питания, другая диагональ – гальванометр. При отношении сопротивлений мостик сбалансирован и по диагонали не протекает ток, стрелка гальванометра стоит на нуле. Мостик выйдет из баланса, когда изменится одно (или несколько) из сопротивлений моста и нарушится вышеприведенное соотношение. При этом стрелка гальванометра отклоняется. Одно из сопротивлений моста это датчик. Датчик (или тензорезистор) это плоская спираль из тонкой константановой проволоки, помещенная между двумя полосками бумаги. Датчик приклеивается к образцу. При растяжении образца растягивается и проволока датчика, изменяется его омическое сопротивление. Мостик выходит из баланса, стрелка гальванометра отклоняется на величину, пропорциональную изменению сопротивления датчика или на величину, пропорциональную деформации слоя материала, к которому приклеен датчик. Чтобы привести мостик в баланс, вращаем ручку реохорда (т.е. изменяем другие сопротивления) до тех пор, пока мостик не сбалансируется и стрелка гальванометра не встанет на ноль. Снимаем показания реохорда. Разность между последующим и предыдущим показаниями реохорда, умноженная на цену деления, и есть величина деформации, соответствующая приложенной нагрузке.
Одно из сопротивлений мостика это компенсационный датчик. Он не нагружен, но реагирует на изменение температуры окружающей среды таким же образом, как и рабочий датчик. Находясь в плече, противоположном рабочему датчику, компенсационный датчик исключает температурный фактор из эксперимента.
Лабораторная работа №6
КОСОЙ ИЗГИБ
Если плоскость изгибающего момента не проходит через главную ось сечения, то такой вид нагружения называется косым изгибом. Главными называются оси, относительно которых центробежный момент инерции равен нулю ( ), а осевые моменты инерции имеют экстремальное значение, то есть один из них это Jmax, а другой Jmin. Заметим, что ось симметрии всегда является главной осью, а вторая главная ось ей перпендикулярна и в наших задачах проходит через центр тяжести сечения.
При косом изгибе балка гнется не в плоскости действия изгибающего момента
(т.е. не в той плоскости, в которой ее гнут), а в некоторой другой, более близкой к плоскости минимальной жесткости.
Нейтральная линия проходит через центр тяжести сечения, но она не перпендикулярна моментной линии. Нейтральная линия отклоняется от перпендикулярного положения к оси минимум. Моментная линия это след моментной плоскости на поперечном сечении.
Определение напряжения
.Для определения напряжений при косом изгибе раскладываем изгибающий момент по главным осям. Следует помнить, что момент носит индекс той оси, вокругкоторой он действует. Проведя нейтральную линию, находим опасную точку как наиболее удаленную от нейтральной линии. Максимальное напряжение в этой точке (назовем ее точкой А) определяем как сумму напряжений от каждого момента отдельно по формуле
, где xA и yA – координаты опасной точки A относительно главных осей x, y.
В нашей задаче разложим силу по главным осям x, y, получим составляющие (рис.1).
Построив эпюры, определим изгибающие моменты в заданном сечении на расстоянии l1 от свободного конца балки
В прямоугольном сечении опасная будет точка в углу (при любом положении нейтральной линии). Напряжение в этой угловой точке
Определение перемещения
Перемещение вычисляем как геометрическую сумму перемещений по главным осям (рис.2).
Перемещение вдоль главной оси определим, перемножив по правилу Верещагина эпюры от нагрузки и от единичного фактора (смотри рис.)
, тогда
.
ЛАБОРАТОРНЫЕ РАБОТЫ ПО СОПРОМАТУ, ЧАСТЬ 1
Работы №1,2,3,4,5,6
1. Механические характеристики материалов, используемые при расчетах на прочность, определяются экспериментально на стандартных образцах.
2. Основными являются испытания на растяжение, сжатие, кручение. В результате испытаний получается кривая в координатах нагрузка – перемещение, называемая характеристикой образца.
3. диаграммой или характеристикой материала — кривая, построенная в координатах напряжение – деформация, С помощью определенных формул
Лабораторная работа №1
ИСПЫТАНИЕ НА РАСТЯЖЕНИЕ ОБРАЗЦОВ МАТЕРИАЛА
Для испытаний на растяжение используется десятикратный образец (рис.1.1 в журнале), у которого l0 = 10 d0. Здесь l0 — длина базы, т.е. размера, изменения которого фиксируются при эксперименте как Δl – удлинение образца, d0 – первоначальный диаметр образца. Образец растягивают до тех пор, пока он не разрушится. После испытаний получается характеристика образца в координатах F, Δl. С помощью формул и из характеристики образца получается диаграмма (характеристика) материала в координатах — напряжение, — деформация.
Испытание малоуглеродистой стали — типичного пластичного материала
Участки характеристики образца:
ОА — линейный участок, материал подчиняется закону Гука, удлинение образца определяется по формуле ; до точки В деформации упруги, то есть они полностью исчезают после разгрузки;
CD — горизонтальный участок диаграммы — площадка текучести, деформации интенсивно нарастают при постоянной нагрузке;
DE — зона упрочнения: в кристаллах металла произошла перестройка, и материал может снова сопротивляться нагружению;
EG — зона разрушения.
В точке Е при в образце возникает местное утонение — шейка. Дальнейшие деформации сосредотачиваются в районе шейки, которая при этом интенсивно утоняется, деформировать образец становится легче и поэтому нагрузка уменьшается. После разрыва образца материал в районе шейки теплый. Это зона больших пластических деформаций, при их образовании материал нагревается.
На характеристике образца с помощью геометрических построений находят характерные точки, соответствующие силам Fпц, Fy, Fт, Fmax, Fраз. Затем по формулам сопромата вычисляют соответствующие напряжения и строят диаграмму (характеристику) материала, с помощью которойопределяют механические характеристики материала:
— предел пропорциональности — наибольшее напряжение, до которого справедлив закон Гука (s = E e);
— предел упругости — наибольшее напряжение, до которого деформации полностью упруги, то есть целиком исчезают при разгрузке;
— предел текучести — напряжение, при котором деформации интенсивно нарастают при постоянной нагрузке;
— предел прочности — напряжение, численно равное максимальной нагрузке, деленной на первоначальную площадь сечения образца.
Характеристика стали называется условной, так как она получена на основании формул и , где A0 и l0 — первоначальная площадь сечения и первоначальная длина образца, в то время как при растяжении изменяются как длина образца, так и размеры его сечения. Если учитывать эти изменения, то получим истинную диаграмму, изображенную тонкой линией на рис. 1.12. Только на истинной диаграмме есть напряжение при разрыве , это самое большое значение напряжения во время испытаний. Amin — площадь сечения шейки в месте разрыва, , dmin — диаметр шейки в месте разрыва. При растяжении стальной образец интенсивно деформируется. Остаточное удлинение после разрыва достигает 30%.
Образец после разрыва
На условной характеристике напряжения при разрыве нет!
В конструкциях, как правило, материал работает при напряжениях, меньших предела текучести. Как видно из рис. 1.12, условная и истинная диаграммы практически совпадают и до значения напряжения, равного пределу текучести sт. Поэтому на практике используют для расчетов условную диаграмму.
Если материал нагрузить за пределы упругости и разгрузить, то при разгрузке исчезнут только упругие деформации, а пластические останутся (рис. 1.14).
Закон разгрузки и повторного нагружения
Если нагрузить материал за пределы упругой зоны (точка К выше точки В, соответствующей пределу упругости, рис. 1.14), а затем разгрузить, то линия разгрузки KL будет параллельна первоначальному участку диаграммы ОА (точка А соответствует пределу пропорциональности). При вторичном нагружении (линия LK) материал сохраняет пропорциональную зависимость между нагрузкой F и удлинением Dl (то есть между s и e) вплоть до максимального напряжения первичного нагружения (точка K), а затем следует по первоначальной кривой КЕ. Это свойство материалов используется на практике, например, при заневоливании пружин. После изготовления пружины нагружают за пределы упругости, увеличивая тем самым величину осадки пружины, пропорциональную силе.
На рис. 1.14:
OАВK — линия первичного нагружения;
KL — линия разгрузки;
OL — пластическое или остаточное удлинение образца;
LM — упругое удлинение, исчезающее при разгрузке;
LKE — линия вторичного нагружения.
Таким образом, удлинение образца в точке K (отрезок ОM на рис. 1.14) с помощью линии разгрузки KL,параллельной первоначальному линейному участкудиаграммы ОА, можно разделить на упругую часть (LM) и пластическую часть (OL).
Условный или технический предел текучести
Некоторые пластичные материалы, например, алюминий, не имеют площадки текучести на диаграмме. Для таких материалов используется условный или технический предел текучести
s0,2 — это напряжение, при котором остаточная деформация равна 0,2%, то есть величина 0,002 в масштабе диаграммы, рис. 1.15.
Для определения s0,2 сначала отложим по оси e величину остаточной деформации, равную 0,002 в масштабе диаграммы. Затем проведем LK÷÷ ОА. Получим пересечение с кривой (точка K). Соответствующее точке K напряжение и есть условный или технический предел текучести s0,2.
Источник
