Лабораторная работа испытание материалов растяжение сжатие
Лабораторная работа № 1
Цель работы – изучить поведение малоуглеродистой стали при растяжении и определить ее механические характеристики.
Основные сведения
Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.
Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.
В таких случаях, кроме металлографических исследований, определяются главные механические характеристики на образцах, взятых из зоны разрушения конструкции. Образцы изготавливаются по ГОСТ 1497-84 и могут иметь различные размеры и форму (рис. 1.1).
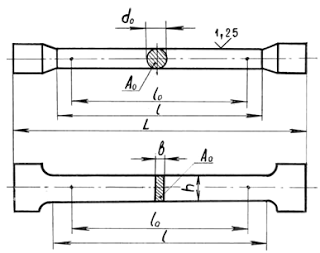
Рис. 1.1. Образцы для испытания на растяжение
Между расчетной длиной образца lо и размерами поперечного сечения Ао (или dо для круглых образцов) выдерживается определенное соотношение:
В испытательных машинах усилие создается либо вручную — механическим приводом, либо гидравлическим приводом, что присуще машинам с большей мощностью.
В данной работе используется универсальная испытательная машина УММ-20 с гидравлическим приводом и максимальным усилием 200 кН, либо учебная универсальная испытательная машина МИ-40КУ (усилие до 40 кН).
Порядок выполнения и обработка результатов
Образец, устанавливаемый в захватах машины, после включения насоса, создающего давление в рабочем цилиндре, будет испытывать деформацию растяжения. В измерительном блоке машины есть шкала с рабочей стрелкой, по которой мы наблюдаем рост передаваемого усилия F.
Зависимость удлинения рабочей части образца от действия растягивающей силы во время испытания отображается на миллиметровке диаграммного аппарата в осях F-Δl (рис. 1.2).
В начале нагружения деформации линейно зависят от сил, потому участок I диаграммы называют участком пропорциональности. После точки В начинается так называемый участок текучести II.
На этой стадии стрелка силоизмерителя как бы спотыкается, приостанавливается, от точки В на диаграмме вычерчивается либо прямая, параллельная горизонтальной оси, либо слегка извилистая линия — деформации растут без увеличения нагрузки. Происходит перестройка структуры материала, устраняются нерегулярности в атомных решетках.
Далее самописец рисует участок самоупрочнения III. При дальнейшем увеличении нагрузки в образце происходят необратимые, большие деформации, в основном концентрирующиеся в зоне с макронарушениями в структуре – там образуется местное сужение — «шейка».
На участке IV фиксируется максимальная нагрузка, затем идет снижение усилия, ибо в зоне «шейки» сечение резко уменьшается, образец разрывается.
При нагружении на участке I в образце возникают только упругие деформации, при дальнейшем нагружении появляются и пластические — остаточные деформации.
Если в стадии самоупрочнения начать разгружать образец (например, от т. С), то самописец будет вычерчивать прямую СО1. На диаграмме фиксируются как упругие деформации Δlу (О1О2), так и остаточные Δlост (ОО1). Теперь образец будет обладать иными характеристиками.
Так, при новом нагружении этого образца будет вычерчиваться диаграмма О1CDЕ, и практически это будет уже другой материал. Эту операцию, называемую наклеп, широко используют, например, в арматурных цехах для улучшения свойств проволоки или арматурных стержней.
Диаграмма растяжения (рис. 1.2) характеризует поведение конкретного образца, но отнюдь не обобщенные свойства материала. Для получения характеристик материала строится условная диаграмма напряжений, на которой откладываются относительные величины – напряжения σ=F/A0 и относительные деформации ε=Δl/l0 (рис. 1.3), где А0, l0 – начальные параметры образца.
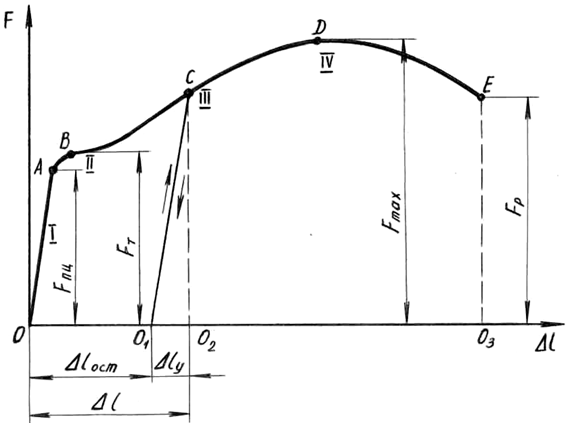
Рис. 1.2. Диаграмма растяжения образца из малоуглеродистой стали
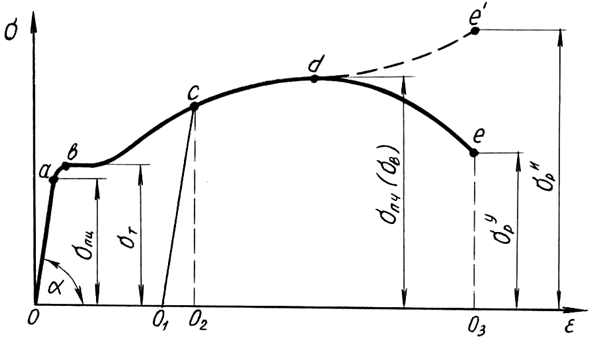
Рис. 1.3. Условная диаграмма напряжений при растяжении
Условная диаграмма напряжений при растяжении позволяет определить следующие характеристики материала (рис. 1.3):
σпц – предел пропорциональности – напряжение, превышение которого приводит к отклонению от закона Гука. После наклепа σпц может быть увеличен на 50-80%;
σу – предел упругости – напряжение, при котором остаточное удлинение достигает 0,05%. Напряжение σу очень близко к σпц и обнаруживается при более тонких испытаниях. В данной работе σу не устанавливается;
σт – предел текучести – напряжение, при котором происходит рост деформаций при постоянной нагрузке.
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют ≈0,2% (рис. 1.4);
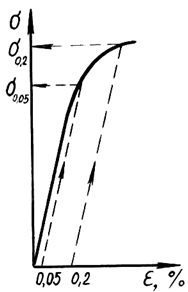
Рис. 1.4. Определение предела упругости и условного предела текучести
σпч (σв) – предел прочности (временное сопротивление) – напряжение, соответствующее максимальной нагрузке;
σр – напряжение разрыва. Определяется условное σур и истинное σир=Fр/Аш, где Аш – площадь сечения «шейки» в месте разрыва.
Определяются также характеристики пластичности – относительное остаточное удлинение
δ = (l1 – l0)∙100% / l0,
где l1 – расчетная длина образца после разрыва,
и относительное остаточное сужение
ψ = (А0 — Аш)∙100% / А0.
По диаграмме напряжений можно приближенно определить модуль упругости I рода
E=σпц/ε=tgα,
причем после операции наклепа σпц возрастает на 20-30%.
Работа, затраченная на разрушение образца W, графически изображается на рис. 1.2 площадью диаграммы OABDEO3. Приближенно эту площадь определяют по формуле:
W = 0,8∙Fmax∙Δlmax.
Удельная работа, затраченная на разрушение образца, говорит о мере сопротивляемости материала разрушению w = W/V, где V = A0∙l0 – объем рабочей части образца.
По полученным прочностным и деформационным характеристикам и справочным таблицам делается вывод по испытуемому материалу о соответствующей марке стали
Контрольные вопросы
- Изобразите диаграмму растяжения образца из малоуглеродистой стали (Ст.3). Покажите полные, упругие и остаточные абсолютные деформации при нагружении силой, большей, чем Fт.
- На каком участке образца происходят основные деформации удлинения? Как это наблюдается на образце? Какие нагрузки фиксируются в этот момент?
- Объясните, почему после образования шейки дальнейшее растяжение происходит при все уменьшающейся нагрузке?
- Перечислите механические характеристики, определяемые в результате испытаний материала на растяжение. Укажите характеристики прочности и пластичности.
- Дайте определение предела пропорциональности.
- Дайте определение предела упругости.
- Дайте определение предела текучести.
- Дайте определение предела прочности.
- Как определить предел текучести при отсутствии площадки текучести? Покажите, как это сделать, по конкретной диаграмме.
- Какие деформации называются упругими, какие остаточными? Укажите их на полученной в лабораторной работе диаграмме растяжения стали.
- Как определяется остаточная деформация после разрушения образца?
- Выделите на диаграмме растяжения образца из мягкой стали упругую часть его полного удлинения для момента действия максимальной силы.
- Какое явление называется наклепом? До какого предела можно довести предел пропорциональности материалов с помощью наклепа?
- Как определяется работа, затраченная на разрушение образца? О каком свойстве материала можно судить по удельной работе, затраченной на разрушение образца?
- Как определить марку стали и допускаемые напряжения для нее после проведения лабораторных испытаний?
- Чем отличается диаграмма истинных напряжений при растяжении от условной диаграммы?
- Можно ли определить модуль упругости материала по диаграмме напряжений?
- Как определить работу, затрачиваемую на деформации текучести лабораторного образца?
Испытание материалов на сжатие >
Краткая теория >
Примеры решения задач >
Источник
Лабораторная работа №3 Испытания на растяжение малоуглеродистой стали
Цель работы:
1.Получить диаграмму растяжения;
2. Определить характеристики прочности материала;
3.Определить характеристики пластичности материала.
Оборудование и приборы:
1.Испытательная разрывная машина WР 300;
2.Штангенциркуль;
3.Образцы (сталь).
Теоретическая часть
При определении качества конструкционных материалов, выпускаемых промышленностью, одним из основных видов испытаний являются испытания на растяжение. Результаты испытаний позволяют судить о прочности материала при статических нагрузках, выбирать материал для проектируемой конструкции. Они являются основными при расчетах на прочность деталей машин и элементов конструкций.
Механические характеристики материалов зависят от многих факторов: вида нагружения, времени воздействия нагрузки, скорости нагружения, температуры, радиации и др.
Наиболее простыми являются испытания материалов при комнатной температуре t=20°С и статическом нагружении, когда dέ /dt~0,01мин-1
Механические характеристики делятся на три группы:
-характеристики прочности;
-характеристики пластичности;
-характеристики вязкости.
Характеристиками прочности измеряют силовую реакцию твердых тел на воздействие внешних нагрузок.Эта реакция постоянна в процессе нагружения и в ней явно прослеживаются несколько характерных зон (см.диаграмму нагружения).К характеристикам прочности относятся: предел пропорциональности, предел упругости. Предел текучести, предел прочности, разрушающее напряжение. Дадим определение этих понятий в порядке возрастания значений их величин.
Предел пророрциональности-это наибольший уровень условного напряжения при котором не наблюдается существенного нарушения закона Гука (каково удлинение, такова сила). Это напряжение определяется по формуле
где Fpγ нагрузка, соответствующая пределу пропорциональности; A0первоначальная площадь поперечного сечения образца.
Предел упругости – это наибольший уровень условного напряжения, при котором материал проявляет упругие свойства, заключающиеся в том, что образец практически полностью восстанавливает свои первоначальные размеры после снятия внешней нагрузки. Его определяют по формуле
где Fe нагрузка, соответствующая пределу упругости.
Предел текучести – это наименьший уровень условного напряжения, при котором наблюдается значительный рост деформаций образца при постоянной (или слегка уменьшающейся) нагрузке. Этот предел определяют по формуле
где Fy нагрузка, соответствующая пределу текучести.
Если в поведении материала не прослеживается площадка текучести (см. диаграмму нагружения) и стрелка силоизмерителя не останавливается на некоторый промежуток времени, то определяют условный предел текучести, соответствующий относительной деформации образца έ=0,002 или 0,2 %:
Предел прочности, чаще называемый временным сопротивлением, – это условное напряжение, соответствующее наибольшему уровню нагрузки, воспринимаемому образцом. Находят эту величину по формуле
где Fu наибольшая нагрузка на образец.
Разрушающее напряжение – это напряжение, при котором происходит разрыв образца. Этот предел не имеет особого практического значения и используется только при изучении процесса образования трещин. Разрушающие напряжения делятся на условные и истинные:
Условное
истинное
где Ffy разрушающая нагрузка; A1— площадь поперечного сечения образца в месте разрыва.
Так как первоначальная площадь A0 приблизительно в два раза превышает площадь разрыва A1, а разрушающая нагрузка Ffy составляет приблизительно 80 % от наибольшей нагрузки Fu, то
Характеристиками пластичности измеряют деформативную реакцию твёрдых тел, т.е. их способность изменять свои размеры под воздействием нагрузок. Пластичность материала характеризуют две величины:
— относительное остаточное удлинение образца (в процентах)
— относительное остаточное сужение поперечного сечения (в процентах)
В этих формулах ℓ0, A0 длина расчётной части и площадь сечения до нагружения; ℓ1, A1 то же после разрыва образца.
Характеристикой вязкости измеряют способность твёрдых тел сопротивляться импульсному и ударному воздействию нагрузок. Количественным показателем этой характеристики является удельная работа внешних сил, затрачиваемая на деформирование и разрушение единицы объёма материала:
где W – работа, совершаемая машиной на растяжение образца вплоть до его разрыва; V0=A0ℓ0- объём расчётной части образца.
Для испытания на растяжение используются специально изготовленные образцы, которые вытачиваются из прутка или вырезаются из листа. Основной особенностью этих образцов является наличие длинной, сравнительно тонкой рабочей части и усиленных мест (головок) по концам для захвата.
Проводятся испытания цилиндрического образца, форма и размеры которого приведены на рис. 1.

Рис.1. Цилиндрический образец:
ℓ0=10d — расчетная длина образца, ℓ1=12,5√F — рабочая длина образца, ℓ2=10√F−ℓ0∕2 — длина конусообразной части образца, ℓ3=d — длина головки образца, L — полная длина образца , d=1,13√F — диаметр сечения расчетной и рабочей длины, d1=1,5√F — диаметр основания конуса (у головки), d2=2√F — диаметр головки образца.
Для замера деформаций на расчетной части образца отмечают отрезок, называемый расчетной длиной. Чаще всего применяются цилиндрические образцы, у которых расчетная длина равна десяти диаметрам (длинные образцы) и образцы с расчетной длиной равной пяти диаметрам (короткие образцы). Чтобы результаты испытаний образцов прямоугольного и круглого сечений были сопоставимы, в случае прямоугольного сечения в качестве характеристики, определяющей расчетную длину, принимается диаметр равновеликого круга.
На рис. 2 показан эскиз пропорционального цилиндрического образца до нагружения и после его разрыва.
Для получения сравнимых результатов испытаний образцы с цилиндрической или прямоугольной формой поперечного сечения рабочей части изготавливаются по ГОСТ 1497-84.

Рис. 2. Образец для испытания на растяжение: а – до нагружения; б – после разрыва
ДИАГРАММОЙ РАСТЯЖЕНИЯ называется график, показывающий функциональную зависимость между нагрузкой и деформацией при статическом растяжении образца до его разрыва. Эта диаграмма вычерчивается автоматически на разрывной машине специальным приспособлением. В нашей лаборатории для этой цели используется разрывная машина Р-10.
На рис. 3 показан примерный вид параметрической диаграммы растяжения малоуглеродистой стали в координатах: абсолютное удлинение Δℓ(t) − нагрузка F(t). В качестве параметра здесь выступает время нагружения, которое для простоты обычно не показывают.

Так как испытание проводят на гидравлической машине, в которой деформация является первичной (), а нагрузка вторичной (), то осью абсцисс (аргументом) является абсолютное удлинение Δℓ, а осью ординат (функцией) – нагрузка F, т.е. фактически мы имеем зависимость F=f(Δℓ), интерпретированную Гуком, проводившим опыты в упруго-пропорциональной зоне нагружения: «каково удлинение, такова сила». Однако в современной трактовке, с учётом того что в реальных условиях эксплуатации машин и сооружений первичной является нагрузка, функциональную зависимость обращают, полагая, что Δℓ=f(F), и обсуждают, как изменяется деформация образца в зависимости от нагрузки (какова сила, таково удлинение).
На диаграмме растяжения OABCDEG показаны 7 характерных точек, соответствующих определённому уровню нагрузки и ограничивающих 6 различных зон деформирования:
OA – зона пропорциональности (линейной упругости);
AB – зона нелинейной упругости;
BC – зона упругопластических деформаций;
CD – зона текучести (пластических деформаций);
DE – зона упрочнения;
EG – зона закритических деформаций.
На участке OA смещение атомов монокристаллов пропорционально приложенной нагрузке. Дефекты кристаллической решётки практически не проявляются.
На участке OB материал ведёт себя упруго. Поведение кристаллической решётки на участке AB характеризуется небольшой нелинейностью. Нужно заметить, что на участке пропорциональности OA материал ведёт себя одновременно и как абсолютно упругий (т. B всегда выше т. A).
На участке BC наблюдается нарастающая нелинейность в деформировании кристаллической решётки. Для выхода новых дислокаций (нарушений строения кристаллов) на поверхность монокристаллов требуется всё меньшее приращение внешней нагрузки .
На участке CD, называемом площадкой текучести, происходит лавинообразный выход дислокаций на поверхность, что приводит к значительному удлинению образца при почти постоянном уровне нагрузки, когда .
На участке DE после выхода на поверхность большей части дефектов кристаллической решётки материал самоупрочняется, и образец всё ещё способен воспринимать некоторое приращение нагрузки. Однако расстояние между атомами постепенно достигает критического значения (приблизительно в два раза больше первоначального), за которым происходит «разрыв» внутренних связей. При подходе к т. E деформации начинают локализоваться в области наиболее слабого сечения, где зарождается шейка образца.
На участке EG заканчивается формирование шейки. Происходит лавинообразное разрушение связей, когда процесс деформирования уже необратим и временное равновесие между внутренними силами и внешней нагрузкой возможно только при уменьшении последней. В т. G происходит разрыв образца. Его размеры восстанавливаются на величину упругой деформации, которая на 2 – 3 порядка меньше остаточных пластических деформаций. У многих материалов разрушение происходит без заметногообразования шейки.
Источник
Лабораторная работа № 2
Цель работы – изучить поведение различных материалов и определить их механические характеристики при статическом сжатии.
Основные сведения
Испытания материалов на сжатие проводят на специальных прессах или универсальных испытательных машинах по специальным методикам: для стали и чугуна используется ГОСТ 25.503-80, бетона — ГОСТ 10.180-90, древесины поперек волокон ГОСТ 16483.11-72, древесины вдоль волокон ГОСТ 16483.10-73.
Параметры образцов, видео и результаты испытаний на сжатие:
- стали
- чугуна
- дерева вдоль волокон
- дерева поперек волокон
- бетона (цементного образца)
Образцы материалов для испытания на сжатие изготовляются в виде цилиндров высотой h и диаметром d . Для чугуна, например, рекомендуется диаметр от 10 до 25 мм. Отношение h/d должно быть в пределах от 1 до 2. При значении h/d >2 сказывается влияние продольного изгиба. При значении h/d<1 в большей степени сказывается влияние сил трения, возникающих между торцами образца и опорными плитами машины.
Силы трения тормозят развитие деформации у торцов образца, чем и объясняется его бочкообразная форма в результате испытаний. Одним из способов уменьшения сил трения является смазывание торцов образца графитом, графитовой смазкой или парафином.
Образцы из искусственного камня (цементного или иного раствора) изготавливаются в виде кубиков или цилиндров.
Деревянные образцы изготавливают в виде прямоугольной призмы с основанием 20 х 20 мм и высотой вдоль волокон 30 мм или кубиков со стороной 20 мм и более.
Пластичные материалы (мягкая сталь, медь и др.) одинаково хорошо работают на растяжение и сжатие, поэтому испытание на сжатие является дополнением к испытанию этих материалов на растяжение.
Для пластичных материалов модуль упругости Е, предел упругости и предел текучести при сжатии примерно те же, что и при растяжении. При сжатии пластичных материалов сила постоянно возрастает (кривая I рис. 2.1), при этом величину напряжений, соответствующих разрушающей силе, определить невозможно, так как образец не разрушается, а превращается в диск (рис. 2.2,а).
Характеристики, аналогичные относительному удлинению и относительному сужению при разрыве, при испытании на сжатие также получить невозможно.
Испытанию на сжатие подвергают главным образом хрупкие материалы, которые, как правило, лучше сопротивляются сжатию, чем растяжению, и применяются для изготовления элементов, работающих на сжатие. Для их расчета на прочность необходимо знать характеристики материалов, получаемые при испытании на сжатие.
На рис. 2.1 кривая 2 показывает диаграмму сжатия чугуна, из которой видно, что закон Гука выполняется лишь приближенно в начальной стадии нагружения.
Верхняя точка диаграммы соответствует разрушающей нагрузке Fmax, определив которую, вычисляют предел прочности материала на сжатие σспч=Fmax/A
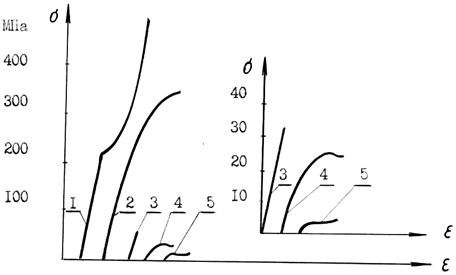
Рис. 2.1. Диаграммы сжатия:
1 – малоуглеродистой стали; 2 – чугуна; 3 – бетона;
4 – сосны вдоль волокон; 5 – сосны поперек волокон
Разрушение чугунного образца происходит внезапно при незначительных остаточных деформациях. Разрушению предшествует образование трещин, расположенных приблизительно под углом 45° к образующим боковой поверхности образца, т.е. по линиям действия максимальных касательных напряжений (рис. 2.2,б).
Характер разрушения образцов из бетона (цементного раствора, камня) показан на рис. 2.2,в – при наличии сил трения между плитами машины и торцами образца. Разрушение происходит путем выкрашивания материала у боковых поверхностей в средней части образца. Трещины образуются под углом 45° к линии действия нагрузки.
При снижении сил трения за счет нанесения слоя парафина на опорные поверхности образца разрушение происходит в виде продольных трещин, материал расслаивается по линиям, параллельным действию сжимающей силы, и сопротивление материала уменьшается (рис. 2.2, г).
Диаграмма сжатия бетона показана на рис. 2.1, кривая 3. Из диаграммы видно, что рост нагрузки сопровождается упругими деформациями вплоть до разрушения, что вообще характерно для хрупких материалов.

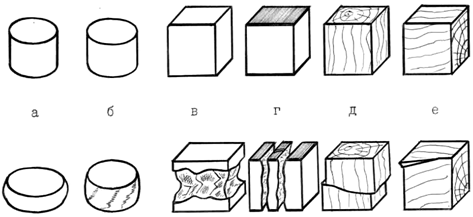
Рис 2.2. Вид образцов из различных материалов до и после испытания на сжатие:
а – малоуглеродистая сталь; б – чугун;
в – цементный раствор без смазки торцов;
г – цементный раствор со смазкой торцов;
д – дерево вдоль волокон;
е – дерево поперек волокон
Особым своеобразием отличается сопротивление сжатию древесины как материала анизотропного и обладающего волокнистой структурой. При сжатии, как и при растяжении, древесина обладает различной прочностью в зависимости от направления сжимавшей силы по отношению к направлению волокон.
Видео сжатия древесины вдоль волокон
Сжатие древесины поперек волокон
На рис. 2.1 изображены диаграммы сжатия образцов из древесины одной породы. Кривая 4 иллюстрирует сжатие образца вдоль волокон, а кривая 5 — поперек волокон. При сжатии вдоль волокон древесина значительно (в 8-10 раз) прочнее, чем при сжатии поперек волокон.
При сжатии вдоль волокон образец разрушается вследствие сдвига одной части относительно другой (рис. 2.2, д), а при сжатии поперек волокон древесина склонна к прессованию и не всегда удается определить момент начала разрушения (рис. 2.2, е).
Порядок выполнения и обработка результатов
Предложенные для испытания образцы замеряют и, поочередно устанавливая их между опорными плитами машины УММ-20, подвергают статическим нагружениям, в процессе которых на диаграммном аппарате производится запись диаграмм сжатия соответствующих материалов. По контрольной стрелке шкалы силоизмерителя фиксируются максимальные нагрузки для каждого из образцов.
По полученным диаграммам сжатия определяют максимальную нагрузку сжатия стального образца и разрушающие нагрузки для других образцов, корректируя их значения с показателями стрелки силоизмерителя, записывают показания в журнал испытаний. Далее определяют характерные значения напряжений и производят записи в журнал испытаний.
Необходимо сделать зарисовку разрушенных образцов и описать характер их разрушения. Дать сравнительную характеристику работы испытанных материалов.
Контрольные вопросы
- Какой вид имеет диаграмма сжатия стали? В чем отличие этой диаграммы от диаграммы растяжения?
- Какие механические характеристики можно определить по диаграмме сжатия стали?
- Каков вид диаграммы сжатия чугуна, бетона? Каков характер разрушения образцов из этих материалов?
- Какие механические характеристики определяют для хрупких материалов при их испытании на сжатие?
- Какой вид имеет диаграмма сжатия дерева вдоль волокон и какие механические характеристики можно определить по ней?
- Как разрушается дерево при сжатии вдоль и поперек волокон? В каком направлений дерево обладает лучшими механическими свойствами?
- Какие характеристики материала можно получить при испытании на сжатие малоуглеродистой стали, чугуна, бетона, дерева?
- Почему образцы из малоуглеродистой стали и из чугуна при сжатии приобретают бочкообразную форму? Почему это явление не наблюдается у бетонных образцов?
Определение модуля упругости I рода для стали >
Примеры решения задач >
Источник
