Лабораторная по сопромату испытание на растяжение
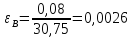
Лабораторная работа №3 Испытания на растяжение малоуглеродистой стали
Цель работы:
1.Получить диаграмму растяжения;
2. Определить характеристики прочности материала;
3.Определить характеристики пластичности материала.
Оборудование и приборы:
1.Испытательная разрывная машина WР 300;
2.Штангенциркуль;
3.Образцы (сталь).
Теоретическая часть
При определении качества конструкционных материалов, выпускаемых промышленностью, одним из основных видов испытаний являются испытания на растяжение. Результаты испытаний позволяют судить о прочности материала при статических нагрузках, выбирать материал для проектируемой конструкции. Они являются основными при расчетах на прочность деталей машин и элементов конструкций.
Механические характеристики материалов зависят от многих факторов: вида нагружения, времени воздействия нагрузки, скорости нагружения, температуры, радиации и др.
Наиболее простыми являются испытания материалов при комнатной температуре t=20°С и статическом нагружении, когда dέ /dt~0,01мин-1
Механические характеристики делятся на три группы:
-характеристики прочности;
-характеристики пластичности;
-характеристики вязкости.
Характеристиками прочности измеряют силовую реакцию твердых тел на воздействие внешних нагрузок.Эта реакция постоянна в процессе нагружения и в ней явно прослеживаются несколько характерных зон (см.диаграмму нагружения).К характеристикам прочности относятся: предел пропорциональности, предел упругости. Предел текучести, предел прочности, разрушающее напряжение. Дадим определение этих понятий в порядке возрастания значений их величин.
Предел пророрциональности-это наибольший уровень условного напряжения при котором не наблюдается существенного нарушения закона Гука (каково удлинение, такова сила). Это напряжение определяется по формуле
где Fpγ нагрузка, соответствующая пределу пропорциональности; A0первоначальная площадь поперечного сечения образца.
Предел упругости – это наибольший уровень условного напряжения, при котором материал проявляет упругие свойства, заключающиеся в том, что образец практически полностью восстанавливает свои первоначальные размеры после снятия внешней нагрузки. Его определяют по формуле
где Fe нагрузка, соответствующая пределу упругости.
Предел текучести – это наименьший уровень условного напряжения, при котором наблюдается значительный рост деформаций образца при постоянной (или слегка уменьшающейся) нагрузке. Этот предел определяют по формуле
где Fy нагрузка, соответствующая пределу текучести.
Если в поведении материала не прослеживается площадка текучести (см. диаграмму нагружения) и стрелка силоизмерителя не останавливается на некоторый промежуток времени, то определяют условный предел текучести, соответствующий относительной деформации образца έ=0,002 или 0,2 %:
Предел прочности, чаще называемый временным сопротивлением, – это условное напряжение, соответствующее наибольшему уровню нагрузки, воспринимаемому образцом. Находят эту величину по формуле
где Fu наибольшая нагрузка на образец.
Разрушающее напряжение – это напряжение, при котором происходит разрыв образца. Этот предел не имеет особого практического значения и используется только при изучении процесса образования трещин. Разрушающие напряжения делятся на условные и истинные:
Условное
истинное
где Ffy разрушающая нагрузка; A1— площадь поперечного сечения образца в месте разрыва.
Так как первоначальная площадь A0 приблизительно в два раза превышает площадь разрыва A1, а разрушающая нагрузка Ffy составляет приблизительно 80 % от наибольшей нагрузки Fu, то
Характеристиками пластичности измеряют деформативную реакцию твёрдых тел, т.е. их способность изменять свои размеры под воздействием нагрузок. Пластичность материала характеризуют две величины:
— относительное остаточное удлинение образца (в процентах)
— относительное остаточное сужение поперечного сечения (в процентах)
В этих формулах ℓ0, A0 длина расчётной части и площадь сечения до нагружения; ℓ1, A1 то же после разрыва образца.
Характеристикой вязкости измеряют способность твёрдых тел сопротивляться импульсному и ударному воздействию нагрузок. Количественным показателем этой характеристики является удельная работа внешних сил, затрачиваемая на деформирование и разрушение единицы объёма материала:
где W – работа, совершаемая машиной на растяжение образца вплоть до его разрыва; V0=A0ℓ0- объём расчётной части образца.
Для испытания на растяжение используются специально изготовленные образцы, которые вытачиваются из прутка или вырезаются из листа. Основной особенностью этих образцов является наличие длинной, сравнительно тонкой рабочей части и усиленных мест (головок) по концам для захвата.
Проводятся испытания цилиндрического образца, форма и размеры которого приведены на рис. 1.

Рис.1. Цилиндрический образец:
ℓ0=10d — расчетная длина образца, ℓ1=12,5√F — рабочая длина образца, ℓ2=10√F−ℓ0∕2 — длина конусообразной части образца, ℓ3=d — длина головки образца, L — полная длина образца , d=1,13√F — диаметр сечения расчетной и рабочей длины, d1=1,5√F — диаметр основания конуса (у головки), d2=2√F — диаметр головки образца.
Для замера деформаций на расчетной части образца отмечают отрезок, называемый расчетной длиной. Чаще всего применяются цилиндрические образцы, у которых расчетная длина равна десяти диаметрам (длинные образцы) и образцы с расчетной длиной равной пяти диаметрам (короткие образцы). Чтобы результаты испытаний образцов прямоугольного и круглого сечений были сопоставимы, в случае прямоугольного сечения в качестве характеристики, определяющей расчетную длину, принимается диаметр равновеликого круга.
На рис. 2 показан эскиз пропорционального цилиндрического образца до нагружения и после его разрыва.
Для получения сравнимых результатов испытаний образцы с цилиндрической или прямоугольной формой поперечного сечения рабочей части изготавливаются по ГОСТ 1497-84.

Рис. 2. Образец для испытания на растяжение: а – до нагружения; б – после разрыва
ДИАГРАММОЙ РАСТЯЖЕНИЯ называется график, показывающий функциональную зависимость между нагрузкой и деформацией при статическом растяжении образца до его разрыва. Эта диаграмма вычерчивается автоматически на разрывной машине специальным приспособлением. В нашей лаборатории для этой цели используется разрывная машина Р-10.
На рис. 3 показан примерный вид параметрической диаграммы растяжения малоуглеродистой стали в координатах: абсолютное удлинение Δℓ(t) − нагрузка F(t). В качестве параметра здесь выступает время нагружения, которое для простоты обычно не показывают.

Так как испытание проводят на гидравлической машине, в которой деформация является первичной (), а нагрузка вторичной (), то осью абсцисс (аргументом) является абсолютное удлинение Δℓ, а осью ординат (функцией) – нагрузка F, т.е. фактически мы имеем зависимость F=f(Δℓ), интерпретированную Гуком, проводившим опыты в упруго-пропорциональной зоне нагружения: «каково удлинение, такова сила». Однако в современной трактовке, с учётом того что в реальных условиях эксплуатации машин и сооружений первичной является нагрузка, функциональную зависимость обращают, полагая, что Δℓ=f(F), и обсуждают, как изменяется деформация образца в зависимости от нагрузки (какова сила, таково удлинение).
На диаграмме растяжения OABCDEG показаны 7 характерных точек, соответствующих определённому уровню нагрузки и ограничивающих 6 различных зон деформирования:
OA – зона пропорциональности (линейной упругости);
AB – зона нелинейной упругости;
BC – зона упругопластических деформаций;
CD – зона текучести (пластических деформаций);
DE – зона упрочнения;
EG – зона закритических деформаций.
На участке OA смещение атомов монокристаллов пропорционально приложенной нагрузке. Дефекты кристаллической решётки практически не проявляются.
На участке OB материал ведёт себя упруго. Поведение кристаллической решётки на участке AB характеризуется небольшой нелинейностью. Нужно заметить, что на участке пропорциональности OA материал ведёт себя одновременно и как абсолютно упругий (т. B всегда выше т. A).
На участке BC наблюдается нарастающая нелинейность в деформировании кристаллической решётки. Для выхода новых дислокаций (нарушений строения кристаллов) на поверхность монокристаллов требуется всё меньшее приращение внешней нагрузки .
На участке CD, называемом площадкой текучести, происходит лавинообразный выход дислокаций на поверхность, что приводит к значительному удлинению образца при почти постоянном уровне нагрузки, когда .
На участке DE после выхода на поверхность большей части дефектов кристаллической решётки материал самоупрочняется, и образец всё ещё способен воспринимать некоторое приращение нагрузки. Однако расстояние между атомами постепенно достигает критического значения (приблизительно в два раза больше первоначального), за которым происходит «разрыв» внутренних связей. При подходе к т. E деформации начинают локализоваться в области наиболее слабого сечения, где зарождается шейка образца.
На участке EG заканчивается формирование шейки. Происходит лавинообразное разрушение связей, когда процесс деформирования уже необратим и временное равновесие между внутренними силами и внешней нагрузкой возможно только при уменьшении последней. В т. G происходит разрыв образца. Его размеры восстанавливаются на величину упругой деформации, которая на 2 – 3 порядка меньше остаточных пластических деформаций. У многих материалов разрушение происходит без заметногообразования шейки.
Источник
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО
ОБРАЗОВАНИЯ
«Национальный
исследовательский ядерный университет
«МИФИ»
Озерский
технологический институт – филиал
НИЯУ МИФИ
Кафедра:
ТМ и МАХП
Лабораторная
работа № 1
По
дисциплине «Сопротивление материалов»
Тема:
«Испытание образца на растяжение».
Выполнили | 1ТМ-16Д | Кузнецов |
Петухов | ||
Рючин | ||
Сергеев | ||
Проверил | Друца |
Озёрск
2017
Цель
работы:
получение и исследование диаграммы
растяжения конструкционного материала
и определение его механических
характеристик.
Приборы
и оборудование:
Разрывная
машина ИМ-4Р (рисунок 1.).
Образец
закрепляется головка-ми в зажимах 1 и
2. Нижний зажим 1 соединен с винтом 13
нагружаю-щего механизма. Верхний зажим
2 соединен с силоизмерительным
ме-ханизмом, состоящим из рычага 3 и
маятника 9. При вращении электро-двигателя
14 винт 13 начинает перемещаться вниз, в
связи с чем усилие растяжения передается
на оба зажима, образец и рычажно-маятниковую
измерительную систе-му. Левый конец
рычага 3 поднима-ется, маятник 9
отклоняется, при этом стрелка 8
перемещается по шкале 6, представляющей
собой линейку с делениями, указывая
действующую нагрузку, а перо 7 автоматически
записывает на бумаге, намотанной на
диаграммном барабане 5, кривую в
координатах нагрузка — деформация.
Вращение барабана 5 осуществляется при
помощи двух пар зубчатых колес 4 и 12. 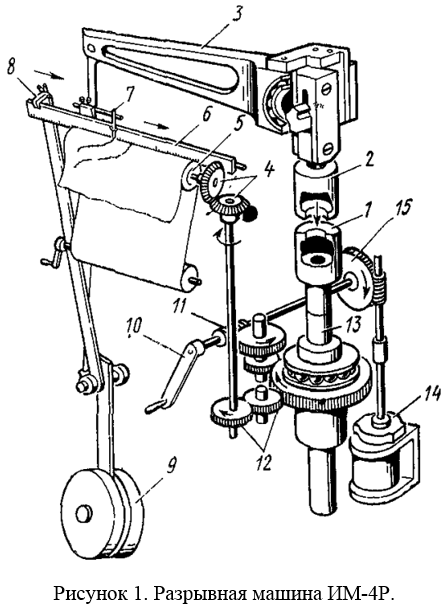
Машина
имеет два привода: электродвигатель,
являющийся нормальным приводом, и
ручной привод, который применяют редко,
например, когда нагружение надо вести
до строго определенной величины.
При
работе с ручным приводом используют
рукоятку 10, которую надо надеть на
правый конец червяка 11. Кроме этого
надо выдвинуть кнопку, находящуюся на
крышке коробки. Это делается для того,
чтобы освободить червяк 11 от сцепления
с осью червячного колеса 15.
Прецизионный
штангенциркуль завода «Калибр»
(рисунок 2.).
Прецизионный
штан-генциркуль состоит из штанги 1 с
губками 7 и 8. На штанге нанесены деления.
По штанге 1 может передви-гаться рамка
4 с губками 6 и 9. К рамке привинчен нони-ус
5. Для грубых измерений передвигают
рамку 4 по штанге 1 и после закрепле-ния
винтом 10 производят отсчет. Для точных
измерений пользуются микрометрической
подачей рамки, состоящей из винта 2,
гайки 3, движка 12 и винта 11. Зажав винт
11 движка, вращением гайки 3 подают рамку
4 до плотного прилегания губок б и 7 или
8 и 9 к измеряемой детали, после чего
производят отсчет.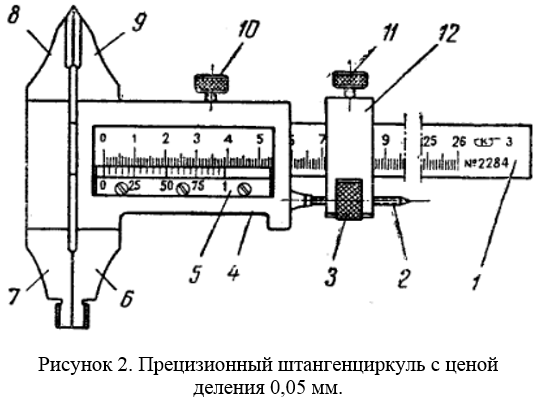
Губки
6 и 7 служат для наружных и внутренних
измерений. При измерении внутренних
размеров к полученным показаниям
прибавляют толщину губок, которая
маркирована на них. Губки 8 и 9 служат
для разметки и наружных измерений.
Ход
работы:
1.
Замерим начальные диаметр и длину
расчётной части исследуемого образца
с помощью штангенциркуля.
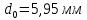 ;
;
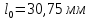 .
.
2.
Произведём растяжение до разрыва
образца на ИМ-4Р с получением диаграммы
нагрузка — деформация на миллиметровой
бумаге.
3.
Замерим диаметр шейки в месте разрыва
и длину расчётной части исследуемого
образца с помощью штангенциркуля.
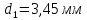 ;
;
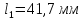 .
.
4.
Обработаем диаграмму растяжения.
4.1
Определим начало координат диаграммы
на миллиметровой бумаге и нанесём
координатные оси.
4.2
Определим масштабы по осям координат.
по
оси абсцисс:
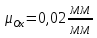 ;
;
по
оси ординат:
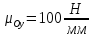 .
.
4.3
Определим по диаграмме растяжения
положение точек A,
C,
D,
K,
соответствующих пределу пропорциональности,
пределу текучести, временному
сопротивлению разрыву, разрыву.
4.4
Для удобства дальнейшей обработки
диаграммы возьмём на ней ещё несколько
дополнительных точек.
4.5
Определим значения нагрузки F
и удлинения Δl
во взятых на диаграмме точках. Полученные
данные сведём в таблицу 1.
5.
Определим значения нормального
напряжения и относительного удлинения
во взятых на диаграмме точках. Полученные
данные сведём в таблицу 1.
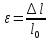 ;
;
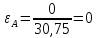 ;
;
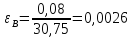 ;
;
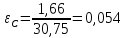 ;
;
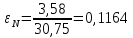 ;
;
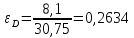 ;
;
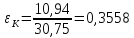 .
.
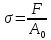 ;
;
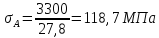 ;
;
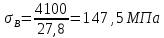 ;
;
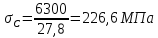 ;
;
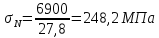 ;
;
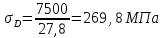 ;
;
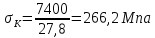 ;
;
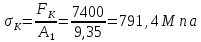 .
.
Таблица | ||||||
Величина | Точки | |||||
A | B | C | N | D | K | |
Нагрузка | 3300 | 4100 | 6300 | 6900 | 7500 | 7400 |
Удлинение | 0,00 | 0,08 | 1,66 | 3,58 | 8,10 | 10,94 |
Нормальные | 118,7 | 147,5 | 226,6 | 248,2 | 269,8 | 266,2 |
791,4 | ||||||
Относительное | 0,00 | 0,0026 | 0,054 | 0,1164 | 0,2634 | 0,3558 |
6.
Построим на основе диаграммы растяжения
образца диаграмму растяжения материала.
Контрольные
вопросы:
1.
Какой вид имеют диаграммы растяжения
образцов малоуглеродистой стали,
легированной стали, чугуна?
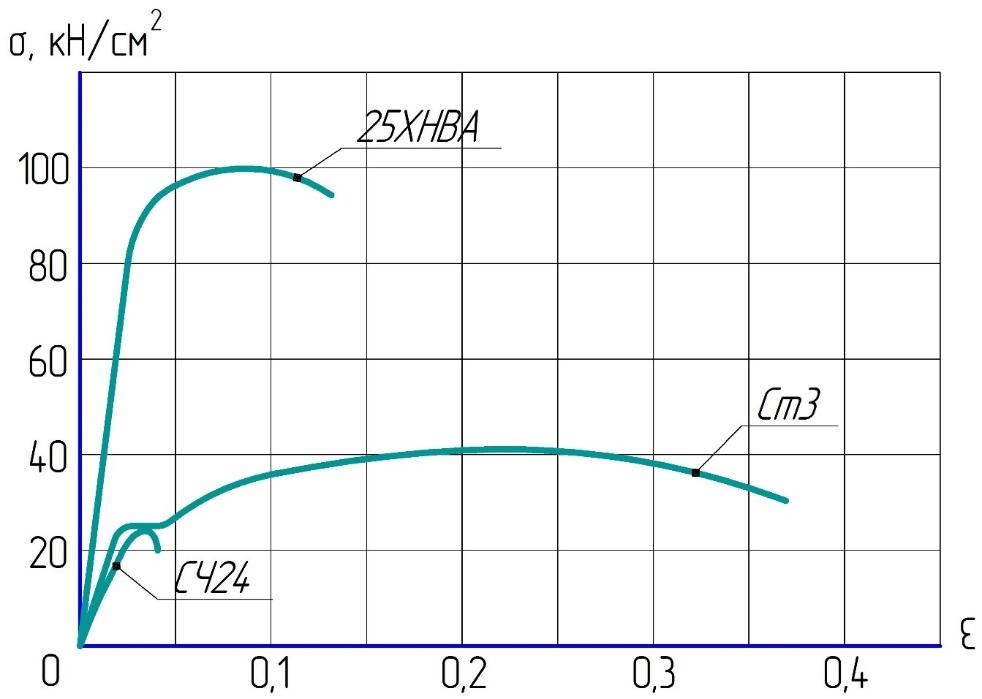
Рисунок
3. Диаграмма растяжения сплавов на
основе железа.
25ХНВА
– малоуглеродистая легированная
качественная конструкционная сталь.
Содержание: углерода – 0,22-0,3 %, хрома –
≤1 %, никеля – ≤1 %, ванадия – ≤1 %.
Ст3
– малоуглеродистая углеродистая
конструкционная сталь обыкновен-ного
качества. Содержание углерода –
0,14-0,22 %.
СЧ-24
–серый чугун с пластинчатым графитом.
Минимальное временное сопротивление
разрыву 240 Мпа.
2.
Как по диаграмме растяжения образца
определить величины упругого и
остаточного удлинений, соответствующих
данной нагрузке?
Необходимо
через точку, соответствующую данной
нагрузке, провести прямую параллельную
участку диаграммы, определяющему
растяжение образца по закону Гука, и
прямую перпендикулярную координатной
оси Ox.
Отрезок между началом координат и
наклонной прямой будет определять
остаточное удлинение, отрезок между
наклонной и перпендикулярной прямыми
будет определять упругое напряжение.
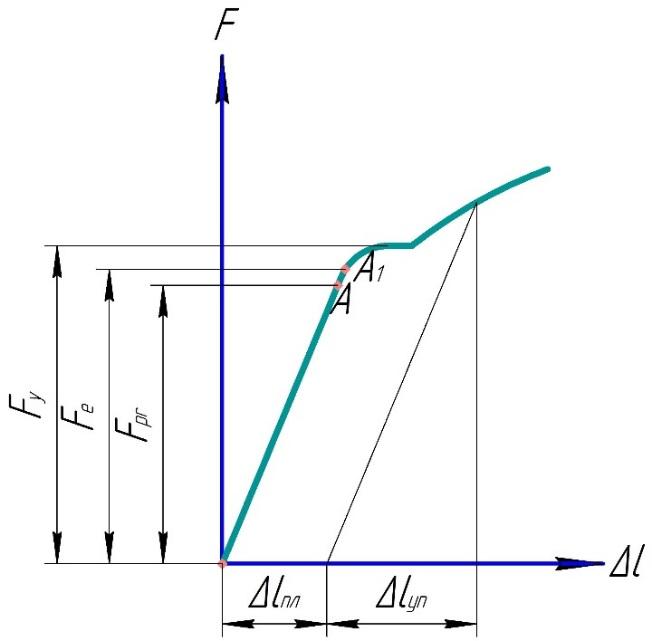
Рисунок
4. Диаграмма растяжения с указанием
способа
определения
остаточного и упругого напряжений.
3.
Что называется физическим и условным
пределом пропорциональности?
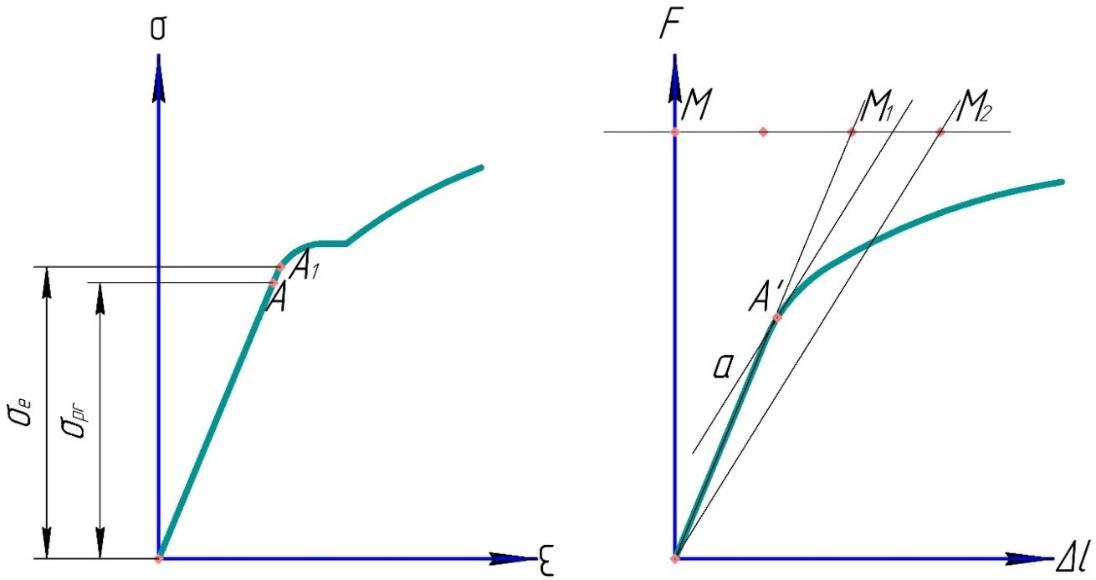
Рисунок
5. Диаграммы растяжения с указанием
физического
и
условного предела пропорциональности.
Физический
предел пропорциональности (т. A
— рисунок 5.) – наибольшее напряжение,
до которого сохраняется прямая
пропорциональная зависимость между
напряжениями и деформациями.
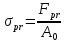 .
.
Условный
предел пропорциональности (т. A’
— рисунок 5.) – напряжение, при котором
отклонение от линейной зависимости
между нагрузкой и удлинением достигает
такой величины, что тангенс угла,
образованного касательной к кривой
деформации
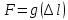
и осью нагрузок увеличивается на 50 %
своего значения на линейном упругом
участке.
4.
Какие механические характеристики
определяют способность материала
пластически деформироваться?
Способность
материала пластически деформироваться
определяет физический, либо условный
предел упругости.
5.
Как на диаграмме растяжения образца
изображаются линии промежуточной
разгрузки и повторного нагружения?
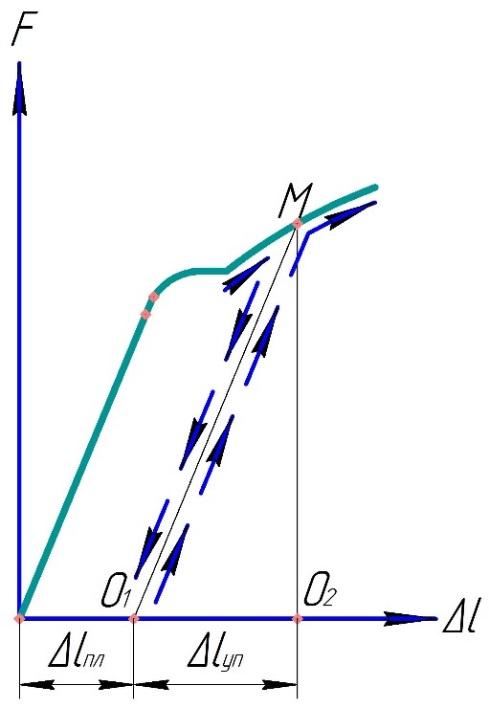
Рисунок
6. Диаграммы
растяжения с указанием линий
промежуточной
разгрузки и повторного нагружения.
Линия
промежуточной разгрузки MO1,
линия повторного нагружения O1M.
6.
С какой целью проводится построение
диаграммы
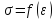 ?
?
Диаграмма
зависимости напряжения от относительного
удлинения является универсальной для
любых значений нагружения, площадей
сечения и длин проектируемых деталей
и их элементов.
Источник
Лабораторная работа 3
Тема: Испытание материалов на растяжение.
Цель
Изучить поведение материала при растяжении до разрушения; получить диаграмму растяжения и установить основные механические характеристики материала образца.
Теоретическое обоснование
Испытание на растяжение является наиболее распространённым видом испытания материалов, так как при нем наиболее ярко выявляются характеристики прочности и пластичности материалов. При определении качества материала, выпускаемого металлургической промышленностью, одним из основных видов испытания также принято испытание на растяжение.

При статических испытаниях на растяжение определяют следующие механические характеристики материалов:
Предел пропорциональности. σпц- наибольшее напряжение, для которого справедлив закон Гука.
Предел упругости. σу- наибольшее напряжение, при котором в образце не возникает остаточных деформаций.
Предел текучести. σт- напряжение при котором происходит рост пластической деформации без заметного увеличения нагрузки.
Предел прочности. σпч- наибольшее условное напряжение, которое определяется делением максимальной нагрузки, выдержанной образцом до разрушения, на первоначальную площадь его поперечного сечения.
Относительное остаточное удлинение при разрыве. σ – величина характеризующая пластичность материала. Она определяется отношением остаточного удлинения образца к его первоначальной длине.
Относительное остаточное сужение. ψ-величина, так же характеризующая пластичность материала. Она определяется отношением изменения площади поперечного сечения образца в месте разрыва к первоначальной площади поперечного сечения.
Машина для испытания.
Для проведения испытаний на растяжение можно использовать универсальную испытательную машину УММ-5, испытательную машину Р-5, пресс Гагарина, испытательные машины ИМ-4Р, ИМ-12А, или ИМ-4А, а также универсальную гидравлическую машину УММ-20 или другие испытательные машины с механическим или гидравлическим приводом, имеющие диаграммный аппарат для регистрации результатов испытаний.
Порядок выполнения работы
1) Эскиз и размеры образца до испытания.
Диаметр d0=10 мм., расчетная длина l0=100 мм., начальная площадь поперечного сечения А0=78,5 мм2.
2) Виды и размеры образца после разрушения.
Диаметр шейки d1=6,5 мм., длина расчётного участка после разрыва l1=126 мм., площадь поперечного сечения образца после разрыва.
3) Схема диаграммы растяжения (с указанием характерных точек).
Усилие текучести Fт=17,3кН., максимальное усилие Fmax=32,2кН., усилие в момент разрыва Fразр=18кН.
4) Результаты испытания:
Предел текучести
![]() =
=![]() *1000=220,38 мПа.
*1000=220,38 мПа.
Временное сопротивление
![]() =
=![]() *1000=410,19 мПа.
*1000=410,19 мПа.
Истинное сопротивление разрыву
![]() =
=![]() *1000=1788,8 мПа.
*1000=1788,8 мПа.
Относительное удлинение
![]() =
=![]() *100%=20,6%.
*100%=20,6%.
Относительное сужение
![]() =
=![]() *100%=77%
*100%=77%
Контрольные вопросы
1) По диаграмме растяжения можно определить пределы прочности, пропорциональности, упругости и текучести.
2) Для участка диаграммы от 0 до 22 кН. справедлив закон Гука.
3) Если материал предварительно вытянуть за предел текучести, то для него не будет справедлив закон Гука, кроме того, в нём будут возникать остаточные деформации, и он будет растягиваться без заметного увеличения нагрузки.
Источник
