Кручение с растяжением внутренние усилия

Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.

Брусья, испытывающие кручение, принято называть валами.

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений: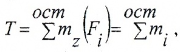

т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

1. поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
2. радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.

Напряжения при кручении

В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле: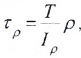

где Iρ — полярный момент инерции.
Эпюра касательных напряжений при кручении имеет следующий вид: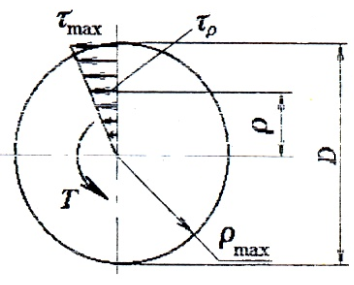

Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρmax: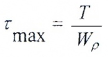

Здесь: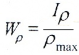

— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала: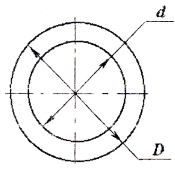


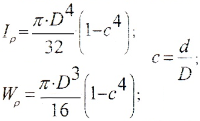
б) для вала сплошного сечения (c=0)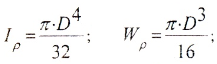

в) для тонкостенной трубы (t0,9)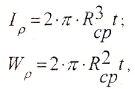

где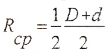

— радиус срединной поверхности трубы.

Деформации

Деформации валов при кручении заключаются в повороте одного сечения относительно другого.

Угол закручивания вала на длине Z определяется по формуле: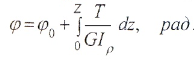

Если крутящий момент и величина GIρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем: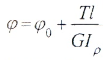

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания: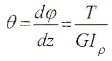

Расчет валов сводится к одновременному выполнению двух условий:

1. условию прочности:
   
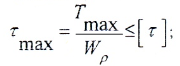
2. условию жесткости:
   

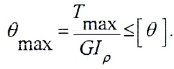
Для стальных валов принимается:

Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:

1. проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
2. Проектировочный расчет, при котором вычисляются диаметры:
   
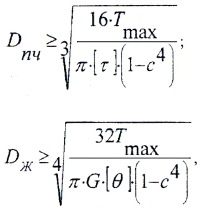
   при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ.
3. Определение грузоподъемности вала:

   Из двух найденных значений крутящего момента необходимо принять меньшее.

При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.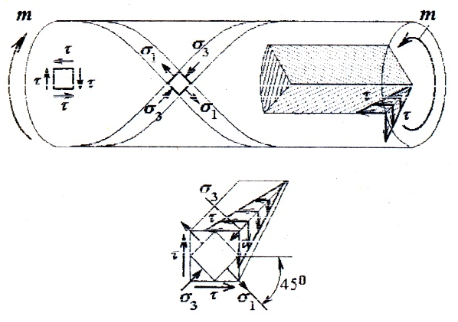

Главные напряжения σ1 = τ, σ3 = -τ наклонены под углом α=±45о к образующей.

Потенциальная энергия упругой деформации определяется по формуле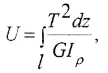

или для участка вала при постоянном T и GIρ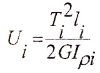

Лекции по сопромату >
Примеры решения задач >

Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.

Внешними нагрузками также являются две противоположно на­правленные пары сил.

Рассмотрим внутренние силовые факторы при кручении круг­лого бруса (рис. 26.1). Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 26.1а). Сечение рассматриваем со стороны отброшенной части.

Внешний момент пары сил разворачивает участок бруса про­тив часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ (рис. 26.1б). Каждая точка сечения имеет симметричную, где возни­кает поперечная сила, направленная в обратную сторону. Эти силы образуют пару с моментом

dm = pdQ;

р — расстояние от точки до центра сечения. Сумма поперечных сил в сечении равна нулю:

С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:

Практически крутящий момент определяется из условия равно­весия отсеченной части бруса.

Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26.1 в):

Эпюры крутящих моментов

Крутящие моменты могут меняться вдоль оси бруса. После опре­деления величин моментов по сечениям строим график-эпюру кру­тящих моментов вдоль оси бруса.

Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае мо­мент внутренних сил упругости направлен против часовой стрелки (рис. 26.2).

Порядок построения эпюры моментов аналогичен построению эпюр продольных сил. Ось эпюры параллельна оси бруса, значения моментов откладывают от оси вверх или вниз, масштаб построения выдерживать обязательно.

Примеры решения задач

Пример 1. На распределительном валу (рис. 26.3) установлены четыре шкива, на вал через шкив 1 подается мощность 12 кВт, кото­рая через шкивы 2, 3, 4 передается потребителю; мощности распреде­ляются следующим образом: Р2 = 8 кВт, Р3 = 3 кВт, Р4 = 1кВт, вал вращается с постоянной скоростью ω = 25 рад/с. Построить эпюру крутящих моментов на валу.

Решение

1. Определяем моменты пар сил на шкивах.

Вращающий момент определяем из формулы мощности при вра­щательном движении

Момент на шкиве 1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противопо­ложное направление. Брус скручивается между движущим момен­том и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:

2. Определяем крутящие моменты в поперечных сечениях бруса с помощью метода сечений.

3. Строим эпюру крутящих моментов. Заметим, что скачок на эпюре всегда численно равен приложенному вращающему моменту.

Выбираем соответствующий масштаб.

Откладываем значения моментов, штрихуем эпюру поперек, об­водим по контуру, записываем значения моментов (см. эпюру под схемой вала (рис. 26.3)). Максимальный крутящий момент на участ­ке III Мкз = 320 Н*м.

Пример 2. Выбрать рациональное расположение колес на валу (рис. 26.5). m1 = 280 Н • м; т2 = 140 Н • м; т3 = 80 Н* м.

Примечание. Меняя местами колеса (шкивы) на валу, можно изменять величины крутящих моментов. Рациональ­ным расположением является такое, при котором крутящие моменты принимают минимальные из возможных значения.

Рассмотрим нагрузки на валу при различном расположении колес.

Из представленных вариантов наиболее рационально располо­жение шкивов в третьем случае, здесь значения крутящих момен­тов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.

Пример 3. Для бруса, изображенного на рис. 2.34, а, построить эпюру крутящих моментов.

Решение

1. Заданный брус имеет три участка I, II, III. Напомним, что границами участков являются сечения, в которых прилажены внешние (скручивающие) моменты.

В данном случае проще, применяя метод сечений, оставлять левую и отбрасывать правую часть бруса — это дает возможность не определять реактивный момент в заделке.

Проводим произвольное поперечное сечение на уча­стке I и составляем уравнение равновесия для оставлен­ной части бруса, изображенной отдельно на рис. 2.34, 6:

В любом сечении участка I крутящий момент имеет найденное значение M1z = т. Из уравнения равновесия для оставленной части значение M1zполучилось со знаком плюс. Это указывает на то, что выбранное направление M1z соответствует действительному.

Эпюра крутящих моментов на этом участке — прямая, параллельная оси абсцисс. Согласно принятому правилу знаков М1я отрицателен, и ординаты эпюры откладываем вниз от ее оси.

2. Проводим произвольное поперечное сечение на участ­ке II и составляем уравнение равновесия для оставлен­ной части бруса, изображенной отдельно на рис. 2.34, в:

Откуда

И в этом случае выбранное направление MIIz соответст­вует действительному. В любом сечении участка II кру­тящий момент MzII= 2m. Согласно принятому правилу знаков, MzIIположителен и ординаты эпюры откладываем вверх от ее оси.

3. Проводим произвольное поперечное сечение на участке III и составляем уравнение равновесия для оставленной части бруса, изображенной отдельно на рис. 2.34, г:

откуда

В любом сечении участка III MzIII = —Зт.

Эпюра крутящих мо­ментов представлена на рис. 2.34, д.

При нагружении бруса сосредоточенными моментами эпюра всегда имеет такой же харак­тер, как и в рассмат­риваемом случае: на от­дельных участках она ограничена прямыми, параллельными оси абсцисс; в местах при­ложения внешних (скру­чивающих) моментов по­лучаются скачки на ве­личину этих моментов.

Пример 4. На вал насажены шкивы 1, 2, 3, 4 (рис. 2.35, а). Шкив 1 передает от ис­точника энергии на вал мощность N1 = 5,2 кВт, а остальные шкивы снимают с вала и передают рабочим машинам мощности соответ­ственно N2 = 1,5 кВт; N3 = 1,7 кВт; N4 = 2,0 кВт. Вал вращается с частотой п = 240 об/мин. Построить эпюру крутящих моментов.

Решение

При построении эпюры крутящих моментов потери в подшипниках не учитываются, поэтому сумма снимаемых с вала мощностей равна подводимой к нему мощности (Л^—N2+Nb+N4). В действительности потери имеют место, но их величина незначительна — не превы­шает 1—2% передаваемой мощности.

Вычислим внешние (скручивающие) моменты, прило­женные к валу:

где

На рис. 2.35,6 показана расчетная схема вала. Вал имеет три участка I, II, III. Эпюра крутящих моментов начинается от середины шкива 1.

На участке I

на участке II

на участке III

Эпюра крутящих моментов показана на рис. 2.35, в.

Поменяем местами шкивы 1 и 2 (рис. 2.36, а). Расчет­ная схема вала показана на рис. 2.36, б.

Эпюра крутящих моментов начинается от середины шкива 2.

На участке I

на участке II

на участке III

Сравнивая эпюры крутящих моментов (см. рис. 2.35, б и 2.36, в), видим, что во втором случае максимальный крутящий момент меньше, чем в первом. Следовательно, второй вариант расположения ведущего шкива предпоч­тительнее.

Контрольные вопросы и задания

1. Какие деформации возникают при кручении?

2. Какие гипотезы выполняются при деформации кручения?

3. Изменяются ли длина и диаметр вала после скручивания?

4. Какие внутренние силовые факторы возникают при круче­нии?

5. Что такое рациональное расположение колес на валу?

6. Для заданного вала (рис. 26.6) выбрать соответствующую эпюру крутящих моментов (а, б, в), m1= 40 Н • м; m2= 180 Н • м; m0= 280 Н • м.

7. В каком порядке рациональнее расположить шкивы на валу для уменьшения нагрузки на вал (рис. 26.7)?

ЛЕКЦИЯ 27

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Построение эпюр крутящих моментов

Иметь представление о деформациях при кручении, о внутрен­них силовых факторах при кручении.

Уметь строить эпюры крутящих моментов.

Деформации при кручении

Кручение круглого бруса происходит при нагружении его па­рами сил с моментами в плоскостях, перпендикулярных продольной оси. При этом образующие бруса искривляются и разворачиваются на угол γ называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол φ, называемый углом закручивания (угол поворота сечения, рис. 26.1).

Длина бруса и размеры поперечного сечения при кручении не изменяются.

Тема 2.5. Кручение. Внутренние силовые факторы при кручении 217

Связь между угловыми деформациями определяется соотноше­нием

l— длина бруса; R — радиус сечения.

Длина бруса значительно больше радиуса сечения, следователь­но, φ » γ.

Угловые деформации при кручении рассчитываются в радиа­нах.

Гипотезы при кручении

1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформа­ции остается плоским и перпендикулярным продольной оси.

2. Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).

3. Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных се­чений не меняются.

Внутренние силовые факторы при кручении

Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.

Внешними нагрузками также являются две противоположно на­правленные пары сил.

Рассмотрим внутренние силовые факторы при кручении круг­лого бруса (рис. 26.1).

Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 26.1а). Сечение рассматриваем со стороны отброшенной части.

Внешний момент пары сил разворачивает участок бруса про­тив часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ (рис. 26.16). Каждая точка сечения имеет симметричную, где возни­кает поперечная сила, направленная в обратную сторону. Эти силы образуют пару с моментом dm = pdQ; p — расстояние от точки

218 Лекция 26

до центра сечения. Сумма поперечных сил в сечении равна нулю: . ΣdQ = 0.

С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:

Практически крутящий момент определяется из условия равно­весия отсеченной части бруса.

Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26.1в):

Эпюры крутящих моментов

Крутящие моменты могут меняться вдоль оси бруса. После определения величин моментов по сечениям строим график-эпюру крутящих моментов вдоль оси бруса.

Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае мо­мент внутренних сил упругости направлен против часовой стрелки (рис. 26.2).

Порядок построения эпюры моментов аналоги­чен построению эпюр про­дольных сил. Ось эпюры параллельна оси бруса, значения моментов откла­дывают от оси вверх или вниз, масштаб построе­ния выдерживать обязательно.

Примеры решения задач

Пример 1.На распределительном валу (рис. 26.3) установлены четыре шкива, на вал через шкив 1 подается мощность 12 кВт, кото­рая через шкивы 2, 3, 4 передается потребителю; мощности распре­деляются следующим образом: Р2 = 8 кВт , Рз = 3 кВт , Р4 = 1кВт ,

Тема 2.5. Кручение. Внутренние силовые факторы при кручении 219

вал вращается с постоянной скоростью ώ = 25 рад/с. Построить эпюру крутящих моментов на валу.

Решение

1. Определяем моменты пар сил на шкивах. Вращающий момент определяем из формулы мощности при вра­щательном движении

Момент на шкиве1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противо­положное направление. Брус скручивается между движущим момен­том и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:

220 Лекция 26

2. Определяем крутящие моменты в поперечных сечениях бруса
с помощью метода сечений.

Сечение I (рис. 26.4а):

— m4 + МК1 = 0; МК1 = m4; МК1 = 40Н • м — крутящий момент отрицательный.

Сечение II (рис. 26.4b):

— m4 – т3 + МК2= 0; МК2 = m4 + m3; МК2 = 40 + 120 = 160Н•м — крутящий момент отрицательный.

Сечение III (рис. 26.4в):

— m4 – т3+ т1 — Мкз = 0; —Мкз = m4 + т3— т1;

-Мкз= 40 + 120 — 480; МКз= 320 Н • м — крутящий момент поло­жительный.

Сечение IV:

MK4= — m4 – т3+ т1 – т2= 0.

3. Строим эпюру крутящих моментов. Заметим, что скачок на
эпюре всегда численно равен приложенному вращающему моменту.

Выбираем соответствующий масштаб.

Откладываем значения моментов, штрихуем эпюру поперек, об­водим по контуру, записываем значения моментов (см. эпюру под схемой вала (рис. 26.3)). Максимальный крутящий момент на участ­ке IIIМкз =320Н•м.

Пример 2.Выбрать рациональное расположение колес на валу (рис. 26.5). т1= 280 Н • м; т2= 140 Н • м; т3= 80 Н • м.

Примечание. Меняя местами колеса (шкивы) на валу, можно изменять величины крутящих моментов. Рациональным рас­положением является такое, при котором крутящие моменты принимают минимальные из возможных значения.

m0 = т1+ т2 + т3 = 280 + 140 + 80 = 500 Н • M.

Тема 2.5. Кручение. Внутренние силовые факторы при кручении 221

Рассмотрим нагрузки на валу при различном расположении колес.

Из представленных вариантов наиболее рационально располо­жение шкивов в третьем случае, здесь значения крутящих момен­тов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.

Контрольные вопросы и задания

1. Какие деформации возникают при кручении?

2. Какие гипотезы выполняются при деформации кручения?

3. Изменяются ли длина и диаметр вала после скручивания?

222 Лекция 26

4. Какие внутренние силовые факторы возникают при кручении?

5. Что такое рациональное расположение колес на валу?

6. Для заданного вала (рис. 26.6) выбрать соответствующую
эпюру крутящих моментов (а, б, в). m1 = 40Н•м; т2 = 180Н•м;
m0 = 280Н•м.

7. В каком порядке рациональнее расположить шкивы на валу
для уменьшения нагрузки на вал (рис. 26.7)?

Тема 2.5. Кручение 223

ЛЕКЦИЯ 27

Тема 2.5. Кручение.

Напряжения и деформации

При кручении

Иметь представление о напряжении и деформациях при круче­нии, о моменте сопротивления при кручении.

Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении.

Напряжения при кручении

Проводим на поверхности бру­са сетку из продольных и попе­речных линий и рассмотрим рису­нок, образовавшийся на поверхно­сти после деформации (рис. 27.1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол φ, продольные линии искривляют­ся, прямоугольники превращают­ся в параллелограммы. Рассмотрим элемент бруса 1234 после деформа­ции.

При выводе формул используем закон Гука при сдвиге и гипотезу

224 Лекция 27

плоских сечений и неискривления радиусов поперечных сечений.

При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27.16).

При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 27.1в), элемент деформируется (рис. 27.1г).

Материал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига.

Закон Гука при сдвиге τ = Gγ,

G — модуль упругости при сдвиге, Н/мм2; γ — угол сдвига, рад.