Косой изгиб с растяжением сжатием
Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения.
Косой изгиб.
Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса.
В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.
Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Условие прочности при косом изгибе:
где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси.
Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности:
где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей.
Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям.
Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей:
Изгиб с растяжением (сжатием).
При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M.
Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса:
К расчёту на прочность бруса при изгибе с растяжением:
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид:
Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле:
где А — площадь поперечного сечения.
Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле:
Условие прочночти имеет вид:
Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям.
Внецентренное растяжение или сжатие.
При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.
К расчёту на прочность бруса при внецентренном растяжении
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Приведём силу F к центру тяжести:
где уF , xF — координаты точки приложения силы F.
В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле:
Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:
Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.
Кручение с изгибом.
Сочетание деформаций изгиба и кручения характерно для работы валов машин.
Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения:
Эпюры напряжений в сечении бруса при кручении с изгибом
Нормальное напряжение достигает максимума на поверхности:
Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала:
Из третьей и четвёртой теории прочности:
При кручении с изгибом условие прочности имеет вид:
Источник
Косой изгиб
Косым изгибом называют такой изгиб стержня, при котором силовая плоскость не совпадает ни с одной из главных плоскостей.
Косой изгиб, вызванный силами, лежащими в одной силовой плоскости, называется плоским косым изгибом. В этом случае изогнутая ось балки представляет собой плоскую кривую, не лежащую
в силовой плоскости.
Если же при косом изгибе действующие на стержень нагрузки не лежат в одной плоскости, то стержень будет испытывать пространственный косой изгиб. В таком случае изогнутая ось — пространственная кривая.
Рассмотрим пример плоского косого изгиба стержня прямоугольного сечения (рис. 7.1, а) [25, 26].
Сила /составляет угол ос с главной вертикальной осью сечения. Разложим силу /’на две составляющие, лежащие в главных плоскостях стержня:
(7.1)
Рх-Р$іпа Ру=Рсо$а.
Каждая составляющая силы /вызовет прямой изгиб: /х — в горизонтальной плоскости (вокруг оси у); Ру — в вертикальной плоскости (вокруг осих).
Следовательно, косой изгиб можно рассматривать как сумму двух прямых изгибов в двух взаимно перпендикулярных плоскостях.
Найдем изгибающие моменты в произвольном сечении, находящемся на расстоянии г от свободного края:
(7.2)
Мх = /уг; Му = /хг.
Нормальное напряжение в произвольной точке К (см. рис. 7 Л, а), имеющей координаты х, у, можно найти как сумму напряжений от двух изгибов (рис. 7.1, б, в):
Рис. 7.1. Косой изгиб стержня:
а — расчетная схема; б — эпюра нормальных напряжений от изгибающего момента Му в — эпюра нормальных напряжений от изгибающего момента Мх
г — составляющие прогиба
Из этого уравнения можно найти положение нейтральной линии сечения, приравняв нормальные напряжения к нулю:
(MX/J;)y + {M,/J,)x=0,
откуда
y = -(MyJx)x/MxJy. (7.4)
Выразим изгибающие моменты Мх и Mv через внешнюю силу F:
у = ~(xF: sin a//7, cos а) (j х /Jv)
у = ~(х$та/со$а)^х^у) = -хХ%а{] х^ Л. (7.5)
Обозначив коэффициент при * через к, получим уравнение вида
У = кх,
где к = -Хёи.(]х/J}>У .
Известно, что это — уравнение прямой, проходящей через начало координат (центр тяжести сечения) и наклоненной под некоторым углом ф к положительному направлению оси х, тангенс которого численно равен коэффициенту пропорциональности к, т. е.
к = Х%ц = -Ща^х/1уУ (7.6)
При прямом изгибе силовая и нейтральная линии сечения были взаимно перпендикулярны. Выясним, будут ли они перпендикулярными и при косом изгибе. Из курса математики известно условие перпендикулярности двух прямых:
к = -1/к1,
где кнкх — угловые коэффициенты прямых, численно равные тангенсам углов наклона этих прямых с положительным направлением оси абсцисс.
Из выражения (7.6) видно, что /х. фJy, tgф?^-tga.
Выразим угол а силовой плоскости через угол (3, который составляет силовая плоскость с положительным направлением оси х:
а = (90° — (3).
Подставим а = (90° — Р) в последнее неравенство:
tgф*-tg(90o-P),
но
tg(90o-P) = ctgP = l/tgP.
Тогда tgф*-l/tgp или
к ф -1Д| .
Это значит, что силовая и нейтральная линии не будут перпендикулярны. Кроме того, нулевая и силовая линии проходят через разные квадранты сечения. Так, в нашем примере силовая линия проходит через первый и третий квадранты, а нулевая — через второй и четвертый.
Зная положение нейтральной линии, легко определить наиболее удаленные от нее точки и, найдя их координаты, вычислить максимальные напряжения в зоне растяжения и сжатия. В приведенном примере это будут точки В и й. В точке й — максимальное напряжение растяжения, в точке В — сжатия:
°0={Мх/-‘Х)У0+{Му/'[у)х0 •
Уп = Ь/2, хп=Ь/2.
Тогда
откуда
Аналогично получим выражение для максимально нагруженной точки в зоне сжатия:
Для сечения простой формы опасная точка находится сразу. В случае сечения сложной формы (рис. 7.2) опасную точку находят графически [24].
Рис. 7.2. Определение опасной точки сечения сложной формы
На вычерченном в масштабе сечении проводят главные центральные оси х и у, строят нейтральную линию, затем, передвигая угольник параллельно нейтральной линии, определяют максимально удаленную точку, координаты хк, ук которой снимают непосредственно с чертежа.
При косом изгибе, как и при прямом, закон распределения напряжений линейный. Зная максимальные напряжения, можно построить эпюру напряжений. Хотя пространственные эпюры более наглядны (рис. 7.1, б, в), чаще строят плоские эпюры. На рис. 7.3 показано построение плоских эпюр для случая, соответствующего рис. 7.1. Условие прочности при косом изгибе будет иметь вид
(7.7)
max
Рис. 7.3. Построение плоских эпюр взамен пространственных
Для выполнения расчетов на жесткость при косом изгибе необходимо знать максимальный полный прогиб, который может быть определен на основе принципа независимости действия сил.
Сначала следует найти отдельно прогибы балки в главных плоскостях так, как это было указано в главе 5, а затем их геометрически сложить.
Так, для нашего примера
fx = F//3EJV = Fsinal3/3EJy ,
fy = F//3EJX = Ecosal}/3EJx полный прогиб свободного конца (рис. 7.1, г) будет равен
/=7л2+Л2 ?
Найдем направление прогиба, обозначив угол между полным прогибом и прогибом в направлении оси х через у.
Тогда
tg У = 4 /Л = (л3 cosa/зял,) ? (зшу If $тЫг) = Jy cosa /J х sin a
/-{/у/1х)Ъ
(7.9)
а =
(7.8)
Подставив (7.9) в выражение (7.8), получим
1ЕУ = (/у/^)[-(1Л8Ф)(/х//>,)] = -1А§Ф,
откуда видно, что направление полного прогиба перпендикулярно к нулевой линии и, следовательно, не совпадает с силовой линией (ранее было показано, что нулевая линия не перпендикулярна силовой), а это, в свою очередь, подчеркивает, что стержень деформируется косо, не в силовой плоскости.
Пример 7.1 [25, 26]. Проверить прочность и жесткость стальной балки, изображенной на рис. 7.4, я, если [о] = 100 МПа, допускаемое значение прогиба 1/1 = //400.
Рис. 7.4. К определению прочности и жесткости балки:
а — расчетная схема; б — эпюра поперечных сил; в — эпюра изгибающих
моментов
Для нахождения момента в опасном сечении строим эпюру изгибающих моментов, предварительно определив реакции. Из симметрии нагружения балки
Ул = У, = чЧ 2-
Опасным будет сечение под серединой балки (рис. 7.4, в), о котором возникает максимальный изгибающий момент
М„ш т, = (?//2)(//2) — («?//2)(//4) = ?/2/8.
Найдем составляющие изгибающего момента:
мтжх = (/2/8)со5ос; Мтаху =(ч12/&упа ,
или, подставив численные значения,
Л/тах,=(и і03-42/8)-0,866 = 1,9 Ю3 Н м,
М
тах у
= (і,2• 103 • 42/8)-0,5 = 1,2-106 Н м.
В точке /) возникают наибольшие напряжения растяжения, а в точке С — сжатия:
а„.с = ±Мх/П’х±Му/Н’у.
Подставив численные значения А/л. и Му и взяв моменты сопротивления сечения из ГОСТ 8239-72: 1?х = 184 см3, ?у = 23,1 см3, получим
адс=±1,9 103/184 10_6±1,2 103/23,М0″6=±62 1 06 Па6 Па.
Найдем прогиб в вертикальной и горизонтальной плоскостях, используя табл. 7.2 [10]: Д. =ц^,=дсо$а; /д = 1840 см4; У^ =115 см4:
/у = (5/384) • {qylЛ|EJx ) = (5 1,2 103 0,866 44)/(384 2 1011 1840-10-8) =
= 0,95 -10_3 м;
/д = (5/384) • (^л./4/?У) = (5 • 1,2 • 103 • 0,5 • 44)/(384 • 2 • 1011 • 115 • 10-8) =
= 8,7-10_3 м.
Полный максимальный прогиб вычислим по формуле
/ = ч/Л2 +1] = А?2 + 0,952 = 8,8 мм.
Найдем 1/1:
[/] = //400 = 4000/400 = 10 мм.
Так как / = 8,8
Источник
Это нагружение получается в случае,
когда сила Рприложена не в плоскости
поперечного сечения (рис.3.4,а). К поперечным
силамPzиPудобавляется
продольная силаN =
Px,
от которой во всех точках поперечного
сечения возникает нормальное напряжение.
В произвольной точке сечения
. (3.12)
Знаки деформации от каждого внутреннего
усилия показаны на рис.3.4,б. Опасная
точка – точка 1. Условие прочности
. (3.13)
а
б
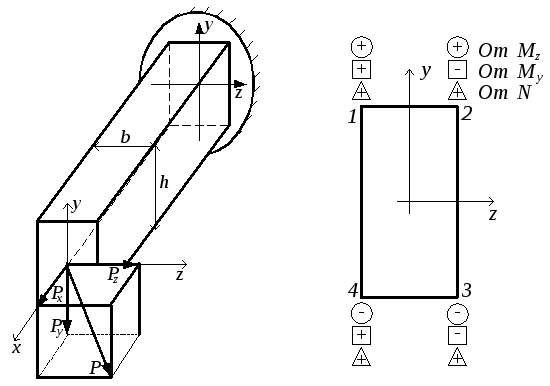
Рис.3.4
Изгиб в двух плоскостях с растяжением
встречается как в паровых, так и в
гидравлических турбинах, где лопасть
(лопатка) нагружена давлением пара или
воды (поперечная нагрузка) и центробежным
усилием (продольная растягивающая
нагрузка).
При расчёте на изгиб со сжатием напряжение,
вызванное продольной силой, подставляется
в формулы (3.12) и (3.13) со знаком «–» (σ =
–N/F).
Ещё раз обращаем внимание на то
обстоятельство, что такой подход
справедлив только для очень жёстких
стержней, у которых вследствие малости
прогибов от поперечных сил можно
пренебречь дополнительным изгибающим
моментом от продольной силы. Для
недостаточно жёстких стержней принцип
независимости действия сил (или принцип
суперпозиции) использован быть не может.
3.4. Внецентренное растяжение (сжатие)
Имеет место при нагружении стержня
силой, параллельной продольной оси и
не совпадающей с центром тяжести сечения.
Эта задача часто встречается в
машиностроении (расчёт станин сверлильного
или фрезерного станков) и в строительстве
(расчёт опор мостов и колонн зданий).
Такое деформирование стержня может
считаться частным случаем рассмотренного
в предыдущем параграфе совместного
действия поперечных и продольной сил.
Рассмотрим внецентренное растяжение
жёсткого стержня (рис.3.5,а), имеющего
поперечное сечение произвольной формы
без углов. Точка приложения силы находится
в первой четверти, координаты её – zpиyp.
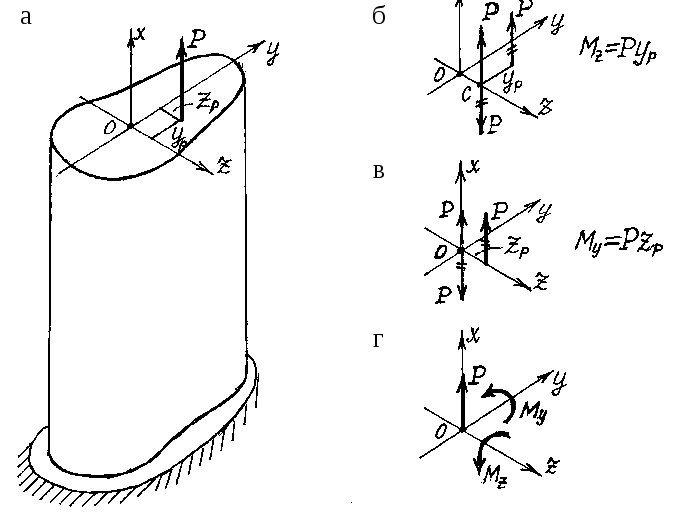
Рис.3.5
Перенесём силу в центр тяжести сечения
в два приёма. Сначала – в точку С на оси
z(рис.3.5,б). Если
в этой точке приложить две равные и
противоположно направленные силыР,
равновесие не нарушится. Дважды
зачёркнутые силы создают моментMz
= P ∙ yp.
Затем переносим силу в центр тяжести
сечения (рис.3.5,в) таким же способом –
возникает моментMy
= P ∙ zp.
Таким образом, при внецентренном
растяжении в поперечном сечении стержня
имеют место три усилия: продольная сила
и два изгибающих момента (рис.3.5,г)
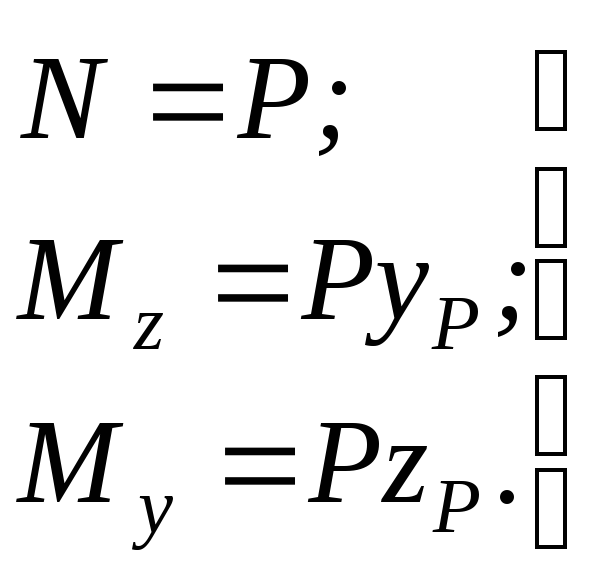. (3.14)
В произвольной точке первой четверти
от всех этих усилий возникнут растягивающие
напряжения, поэтому нормальное напряжение
в любой точке поперечного сечения будет
. (3.15)
Подставляя (3.14) в (3.15), получим
. (3.16)
При определении напряжения в любой
точке сечения необходимо координаты
этой точки zиyподставлять со своими знаками. Обратим
внимание на то обстоятельство, что в
формуле (3.16) отсутствует координатах,
т.е. напряжение постоянно по длине
стержня.
Преобразуем формулу (3.16), вынеся за
скобку P/F,
.
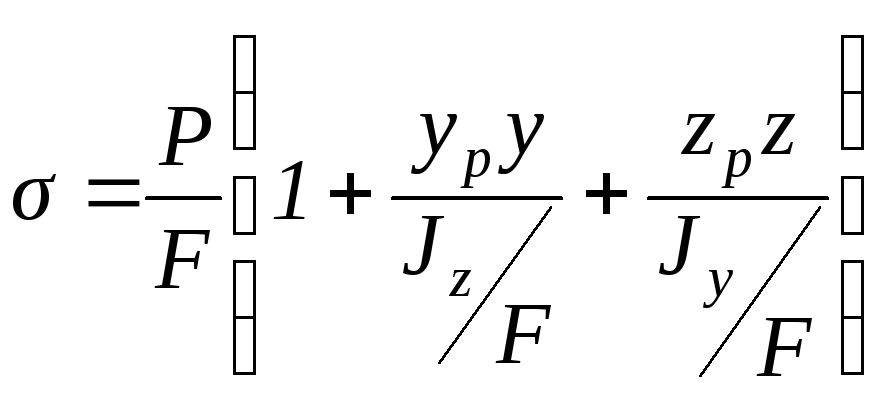Величины,
стоящие в знаменателе второго и третьего
слагаемых, представляют собой квадраты
радиусов инерции сечения (см. формулу
(4.21) на с.66 Ч.1):
,
.
Следовательно,
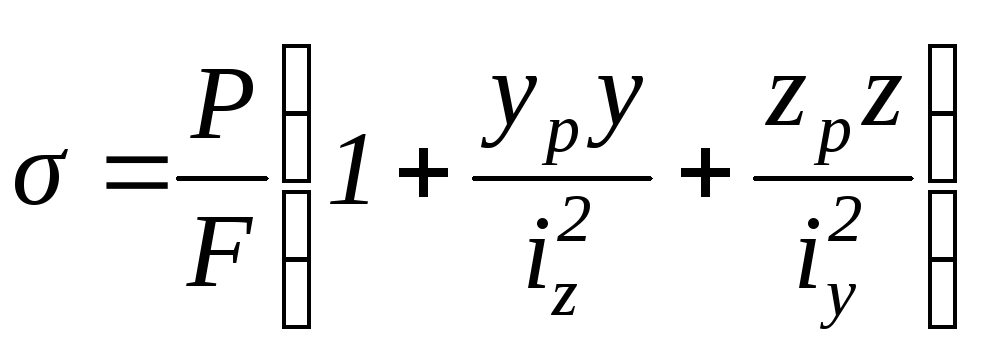(3.17)
Для получения уравнения нейтральной
линии используем формулу (3.17). Обозначим
координаты любой точки нулевой линии
znиyn,
подставим в уравнение (3.17) и приравняем
напряжение к нулю. После сокращения наP/Fполучим уравнение нейтральной линии
. (3.18)
Это
уравнение прямой, не проходящей через
начало координат. Из него можно определить
отрезки, отсекаемые нулевой линией на
осях координат. Обозначим эти отрезки
(рис.3.6) через z
и у.
Если положить zn
= 0, то yn
= у,
а если yn
= 0, то zn
= z.
Из уравнения
(3.18)
,
.
Решая
эти уравнения, получим отрезки, отсекаемые
нулевой линией на осях координат:
,
. (3.19)
Теперь, имея положение нулевой линии,
можно найти наиболее удалённые от неё
точки. Для этого необходимо провести
касательные к сечению, параллельные
нулевой линии. Подставим координаты
точки Св формулу (3.16) и получимσmax;
координаты точкиD–
получимσmin.
Если материал имеет неодинаковую
прочность на растяжение и сжатие, условия
прочности следующие:
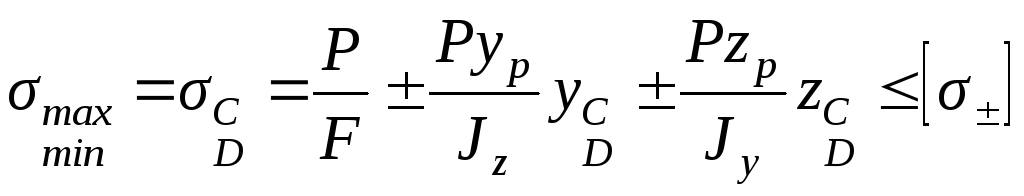. (3.20)
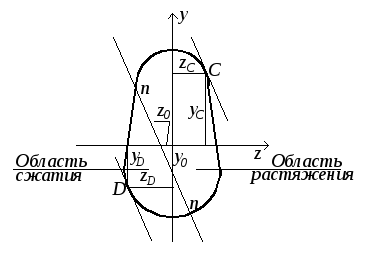
Рис.3.6
Для сечения с углами (рис.3.7) условие
прочности можно записать, не прибегая
к определению положения нейтральной
линии:
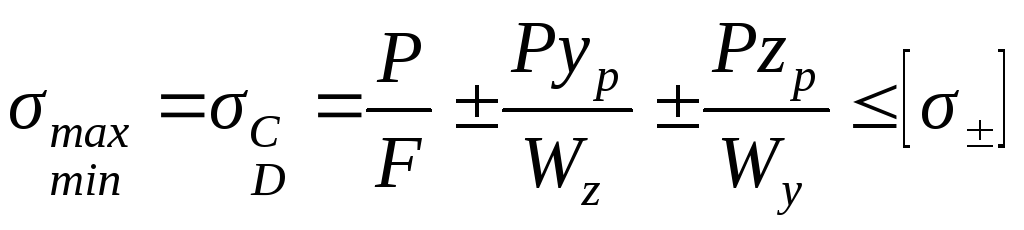. (3.21)
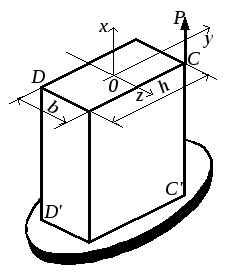
Рис.3.7
В нашем случае:
,
.
,
,
.
Максимальное напряжение имеет место
во всех точках ребра СС′,минимальное
– во всех точках ребраDD′.
В формулах (3.20) и
(3.21) [σ+]
– допускаемое напряжение на растяжение;
[σ-]
– допускаемое напряжение на сжатие.
Рассмотрим теперь частный случай
внецентренного сжатия колонны
прямоугольного сечения, когда одна из
координат точки приложения силы равна
нулю. Пусть сила расположена на оси 0у
(zp
= 0, yp
= ℮), как это показано на рис.3.8.
Подставляя эти значения в формулу
(3.20), получим для крайних волокон
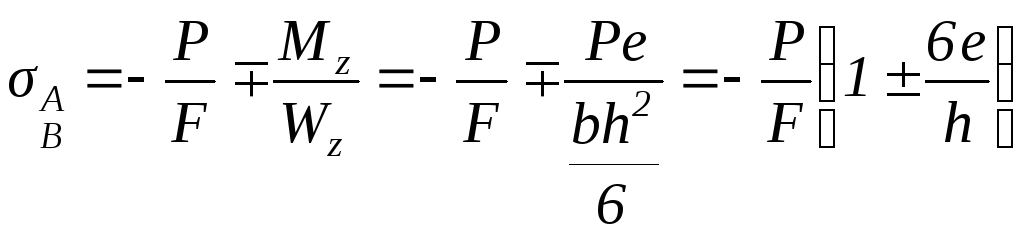. (3.22)
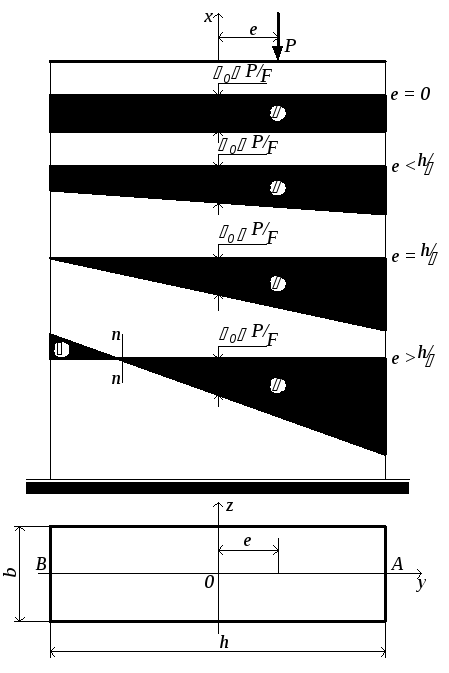
Рис.3.8
Исследуем, как меняется распределение
напряжений в поперечном сечении при
движении силы Рпо оси0у.
Из формулы (3.22)
следует, что при ℮
= 0 напряжения
во всём сечении одинаковые сжимающие.
Если при ℮ =
h/6,
то напряжения во всём сечении одного
знака. В частности, когда ℮
= h/6, напряжения
в точках А
и В
равны: σА
= –2P/F,
σВ
= 0. Если,
наконец, ℮ >
h/6,то
нейтральная ось расположена внутри
сечения. Она разделяет его на две части:
в одной – сжатие, в другой – растяжение.
Таким образом, если не хотят, чтобы в
поперечном сечении появлялись
растягивающие напряжения, нельзя
допускать эксцентриситет силы больше,
чемh/6. Это бывает необходимо, когда
колонна изготавливается из материала
с низкой прочностью на растяжение
(например, бетона, камня, кирпичной
кладки).
Можно найти так называемое ядро сечения
– область вокруг центра тяжести,
характерную тем, что всякая продольная
сила, приложенная внутри этой области,
вызывает во всех точках поперечного
сечения напряжения одного знака. Всякая
сжимающая сила, приложенная где-либо
внутри ядра сечения, вызывает во всём
сечении только сжимающие напряжения,
растягивающая – только растягивающие
напряжения.
Для прямоугольника мы фактически нашли
границы ядра сечения (см.рис.3.8): надо от
центра тяжести отложить по осям в обе
стороны расстояния, равные одной шестой
длины стороны, и соединить точки прямыми
линиями (рис.3.9,а).
Найдём границы ядра сечения для круга.
Ясно, что это тоже будет круг. Если
приложить силу Рв точке С на границе
ядра сечения, то нулевая линия будет
касательной к контуру и перпендикулярной
осиz(рис.3.9,б). Из
формулы (3.19) следует
,
,
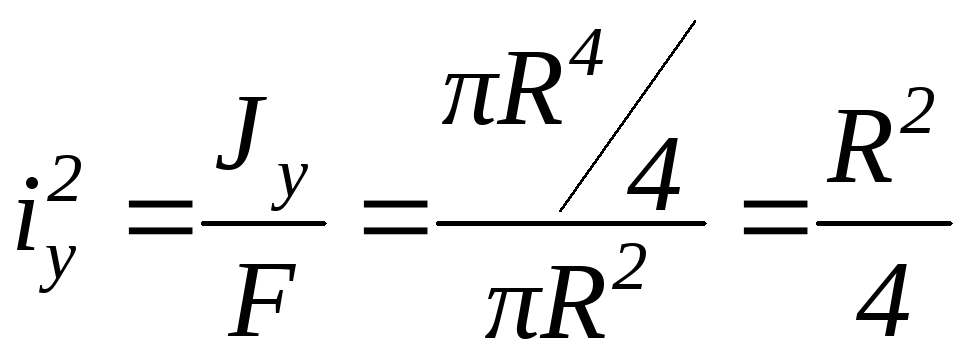,zp
= ℮ = 
.
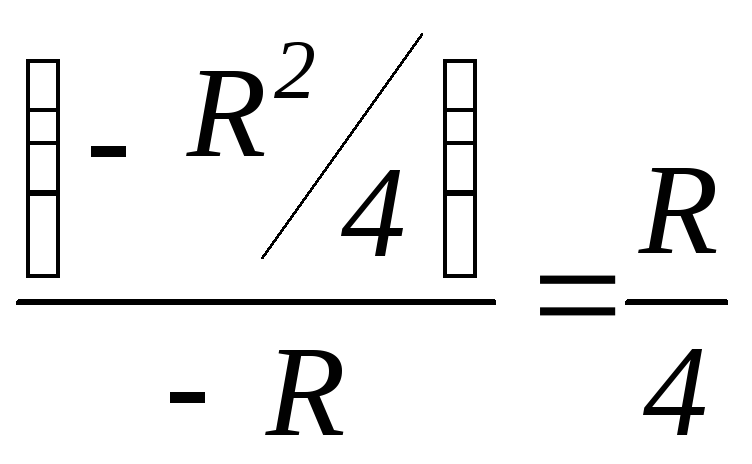Получили,
что для круга ядро сечения – это круг
радиусом
.
а
б
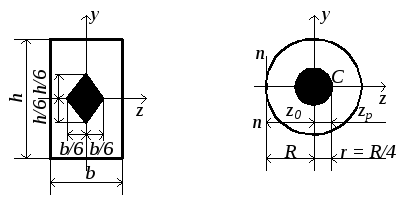
Рис.3.9
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Изгиб с растяжением – частный случай сложного сопротивления, при котором на брус действуют продольные и поперечные нагрузки, пересекающие ось бруса. В общем случае в поперечных сечениях возникают пять внутренних усилий: действующие в двух плоскостях изгибающие моменты Mz, My, поперечные силы Qz, Qy, а также продольная сила N. Возникает сложный изгиб с растяжением или сжатием. Пренебрегая касательными напряжениями от поперечных сил Qz, Qy (для длинных балок с отношением ℓ/h > 10 их влияние незначительно), можно считать напряженное состояние в опасных точках линейным. Внецентренное растяжение или сжатие Внецентренное растяжение – частный случай изгиба с растяжением, при котором брус растягивается силами, параллельными оси бруса так, что их равнодействующая не совпадает с осью бруса, а проходит через точку Р, называемую полюсом силы. Внутренние усилия и напряжения В произвольном сечении х бруса (рис.8.7, а) методом сечений определяем внутренние усилия Рис. 8.6. Примеры деталей и узлов, работающих при внецентренном нагружении: а – болт-костыль; б – пружина сцепления; в – сварное соединение Отличны от нуля три внутренних усилия (рис. 8.7, б), от которых возникают нормальные напряжения, действующие по одной из трех пар граней (рис. 8.7, в); две другие пары граней свободны от напряжений. Имеет место линейное напряженное состояние. Напряжения в произвольной точке являются суммой трех слагаемых Учитывая, что отношение i = – радиус инерции сечения, получим О правиле знаков внутренних усилий. Формула (8.10) выведена для случая положительной растягивающей силы N и изгибающих моментов Mz, My, вызывающих растягивающие напряжения в точке, принадлежащей первой четверти осей координат (где x > 0 и y > 0). Поэтому оси координат поперечного сечения бруса следует направлять так, чтобы полюс P (точка приложения силы) находился в первом квадранте. Если сила, приложенная к брусу, сжимающая, то ее числовое значение будет со знаком минус. Анализ формулы (8.10) 1. Отсутствие координаты х свидетельствует о неизменности напряжений вдоль оси бруса. 2. В случае приложения силы в центр тяжести сечения (zP = 0, yP = 0) напряжения в любой точке сечения постоянны и равны σ = F/A, то есть центральное растяжение является частным случаем внецентренного. Рис. 8.7. Схема к определению внутренних усилий и напряжений при внецентренном приложении силы 3. Независимо от значений координат полюса Р напряжение в центре тяжести сечения (yцт =0, zцт = 0), σцт = F/A. 4. Переменные z и y в первой степени, следовательно, формула (8.10) является уравнением прямой и нормальные напряжения распределяются по линейному закону, значит должна быть нейтральная линия, на которой напряжения равны нулю. Уравнение нейтральной линии при внецентренном растяжении Нейтральная линия (нейтральная ось) – геометрическое место точек, в которых нормальное напряжение в поперечном сечении равно нулю. Приравняем нулю уравнение (8.10). Поскольку F/A ≠ 0, то выражение в скобках равно нулю Переменные z, y в первой степени, следовательно, нормальные напряжения в сечении распределяются по линейной зависимости. Полученное выражение приведем к виду уравнения прямой в отрезках, где a и b – отрезки, отсекаемые линией на осях координат. В нашем случае уравнение нейтральной линии будет записано как Свободный член полученного уравнения не равен нулю, следовательно, нейтральная линия через начало координат не проходит. Отрезки, отсекаемые нейтральной линией на осях y и z, соответственно равны: По найденным значениям отрезков проводят нейтральную линию и находят точки В и С, наиболее удаленные от нее (рис. 8.9). Выполняют это простым геометрическим построением, проводя касательные к сечению, параллельные нейтральной оси. Найденные точки – опасные, поскольку напряжения в них наибольшие по величине. Рис. 8.8. Уравнение прямой в отрезках и график прямой линии, известные из школьного курса Уравнения (8.12), связывающие координаты полюса Р – точки приложения внешней нагрузки с положением нейтральной линии, являются гиперболической функцией. Чем ближе полюс Р к центру тяжести сечения (значения yP, zP уменьшаются), тем нейтральная линия проходит дальше и в пределе стремится к бесконечности. И, наоборот, по мере отдаления точки приложения силы от центра тяжести нейтральная линия асимптотически приближается к нему. Однако пересечь центр тяжести сечения нейтральная линия не может (см. анализ формулы (8.10)). В центре тяжести σцт = F/A (рис. 8.9), поскольку yцт = 0 и zцт = 0 (подставьте в (8.10)). Нейтральная линия может разделять поперечное сечение на области, в которых действуют напряжения разных знаков. Некоторые материалы (чугун, силумин, керамика, кирпичная кладка…) хорошо сопротивляются сжатию и плохо – растяжению. Поэтому необходимо уметь определять такую область приложения нагрузки, в которой не возникают напряжения разных знаков. Ядро сечения Ядро сечения – область вокруг центра тяжести сечения, при приложении нагрузки внутри которой, напряжения во всем сечении будут одного знака. Контур ядра сечения строят путем окатывания нейтральной линией контура поперечного сечения, то есть решают задачу обратную той, в которой определяли положение нейтральной линии: куда следует прикладывать силу, чтобы нейтральная линия не пересекала контур сечения, а только касалась его. Задают несколько положений нейтральной линии, касательной к сечению (например, н.л.1, н.л.2, н.л.3), определяют координаты точек пересечения этих линий с осями координат (например, zн.л.1, yн.л.1). Затем, преобразуя уравнение (11), находят Рис. 8.10. Определение координат отрезков нейтральной линии для построения ядра сечения Рис. 8.9. Эпюра напряжений в поперечном сечении Нейтральная линия соответствующие им координаты точек ядра сечения (точки 1, 2, 3): Так как при переходе нейтральной линии с одной стороны на другую (например, от н.л 3 к н.л 4) она поворачивается вокруг угловой точки сечения, то точка приложения силы перемещается по прямой (на рис. 8.10 отрезок 3 – 4), образуя контур ядра. Пример 8.4. Построить ядро сечения для круга диаметром d. Решение. Квадрат радиуса инерции круга: Задаем положение нейтральной линии 1–1, касательной к окружности. Ее координаты: Координаты точки ядра сечения: Из симметрии сечения относительно его центра тяжести следует, что при других положениях нейтральной линии на окружности диаметром d точки ядра сечения образуют концентрический с ней круг диаметром d/4. Пример 8.5. Построить ядро сечения для прямоугольника с размером сторон bЧh. Решение. Квадраты радиусов инерции: Задаем положение нейтральной линии 1-1, касательной к верхней грани прямоугольника. Ее ко- ординаты: zн.л 1 = ∞; yн.л1 = h/2. Координаты соответствующей точки ядра сечения: Аналогично для нейтральной линии 2-2: zн.л 2 = b/2; yн.л 2 = ∞. Учитывая симметрию прямоугольного сечения относительно осей z и y, задаем положения нейтральных линий на противоположных сторонах прямоугольника и получаем еще две точки. Соединяя все точки, получаем ядро сечения в виде ромба с диагоналями, равными h/3 и b/3. Пример 8.6. Построить ядро сечения для швеллера № 20. Решение. Из таблицы сортамента выпишем исходные данные и выполним рисунок швеллера. Последовательно задаем положение нейтральной линии (I-I, II-II, III-III, IV-IV), касающейся контура сечения, и вычисляем координаты точек ядра сечения. Расчеты представлены в табличном виде. Ядро сечения имеет вид четырехугольника, асимметричного относительно оси ординат. Положение ядра сечения зависит лишь от формы и размеров поперечного сечения, но не зависит от величины приложенной силы. Расчет на прочность при внецентренном нагружении Поверочный расчет выполняют, используя условие прочности Проектный расчет обладает особенностью, связанной с тем, что геометрические характеристики, входящие в условие прочности содержат искомый размер поперечного сечения в разной степени. Площадь А измеряется в м2, а моменты сопротивления W в м3. Попытка выразить искомый yн.л. = h/2 = 20/2 = 10 см; zн.л. = ∞; размер из условия прочности приводит к трансцендентной функции, то есть аналитической функции, не являющейся алгебраической. Проектный расчет выполняют методом итераций 1 [от лат. iteratio – повторение]. В первом приближении, пренебрегая одним из внутренних усилий, – продольной силой N – подбирают размер сечения только из условия прочности при изгибе. Полученный размер подставляют в исходное уравнение и выполняют следующую пробу. Процесс повторяют до тех пор, пока невязка – разность размеров последующей и предыдущей проб, не достигнет заданной наперед малости. Пример 8.7. (Винокуров А. И. Сборник задач … 5.35). Подобрать диаметр стержня выпускного клапана. При расчете использовать усилие F в момент открывания клапана в конце рабочего хода поршня. Решение. Сила давления газов на тарелку клапана 533441Н Внутренние усилия в сечении 1-1 стержня клапана (по модулю): N = F; M = F•e. Условие прочности: По обе стороны от знака неравенства искомый диаметр – имеем трансцендентное уравнение, которое решаем методом приближений: Метод последовательных приближений, при котором каждое новое приближение вычисляют исходя из предыдущего; начальное приближение выбирается в достаточной степени произвольно. Дано: p = 1,5 МПа; e = 12 мм; D = 35 мм; [σ] = 210 МПа Разность между последним и предпоследним приближениями Процесс подбора прекращаем, принимаем d = 10 мм. Проверка: Напряжения изгиба больше напряжений растяжения в 6,9 раза Пример 8.8. (Винокуров А. И. Сборник задач … 5.38.). Из расчета на прочность определить размер h скобы струбцины. Решение. Условие прочности при внецентренном растяжении плоской фигуры σ=+≤[σ] где A = b•h; W = b•h2/6; M = F(a+h/2). Условие прочности: Требуемый размер скобы: Размер h в обеих части неравенства. Полученное уравнение – трансцендентное. Решаем его методом последовательных приближений. В первом приближении принимаем h в скобках под корнем равным нулю: h0 = 0. Тогда Невязка подбора 100 25,4 % Следующее приближение 101,58 мм. Невязка подбора 100 4,5 % Следующее приближение 102,54 мм. Невязка подбора 100 0,95 % невязка менее 1 %, поэтому выходим из цикла подбора. Принимаем h = 103 мм. Проверка: Сопоставим вклады от изгиба и растяжения в общее напряжение: Напряжения от изгиба в 8,24 раза превышают напряжения от растяжения. Полученное соотношение можно сделать более благоприятным снизив долю растягивающих напряжений от изгиба за счет уменьшения плеча е изгибающего момента. На практике применяют тавровое и двутавровое сечения, смещая центр тяжести с ближе к линии действия силы и располагая больше материала в области растягивающих напряжений, к которым хрупкие материалы более чувствительны. Рис. 8.11. Примеры выполнения поперечного сечения бруса, подверженного действию вне?