Как связан модуль сдвига с модулем упругости при растяжении
Наиболее основополагающей моделью материала в механике сплошных сред является модель линейной упругой среды. Как не банально это звучит, но некоторые важные особенности этой модели могут быть не очевидны с первого взгляда. В данной статье мы углубимся в теорию и прикладные аспекты применения этой модели среды и дадим представление об изотропии и анизотропии, допустимых значениях свойств материалов, несжимаемости и влиянии геометрической нелинейности.
Изотропная линейная упругая среда
В подавляющем большинстве случаев при моделировании, включающем применение линейных упругих материалов, имеют дело с изотропной средой, упругие свойства которой не зависят от направления. Для описания такого материала требуется лишь два независимых параметра, определяющих свойства материала. Существует много разных способов выбора этих параметров, однако некоторые из них более популярны, чем другие.
Модуль Юнга, модуль сдвига и коэффициент Пуассона
Модуль Юнга, модуль сдвига и коэффициент Пуассона — наиболее часто встречающиеся в таблицах параметры, описывающие упругие свойства материалов. Они не являются независимыми, так как модуль сдвига, G, связан с модулем Юнга, E, и коэффициентом Пуассона, nu, соотношением
G = frac{E}{2(1+nu)}
Модуль Юнга может быть непосредственно измерен в эксперименте по одноосному растяжению, тогда как модуль сдвига измеряется, например, в эксперименте чистого кручения.
Помимо этого, при одноосном растяжении коэффициент Пуассона определяет, насколько материал будет усаживаться (или, возможно, уширяться) в поперечном направлении. Допустимый диапазон значений составляет -1 <nu< 0.5, где положительные значения указывают на то, что материал становится тоньше при растяжении. Есть несколько материалов, называемых Ауксетиками, которые имеют отрицательный коэффициент Пуассона. Пробка в винной бутылке имеет коэффициент Пуассона близкий к нулю, так что ее диаметр практически не изменяется вне зависимости от того, вытягивают ее или проталкивают.
Для многих металлов и сплавов nu approx1/3, и модуль сдвига, таким образом, составляет около 40% от модуля Юнга.
С учетом возможных значений nu допустимые значения отношения модуля сдвига к модулю Юнга лежат внутри интервала
frac{1}{3} < frac{G}{E} < infty
Когда значение nu приближается к 0.5, материал становится несжимаемым. При анализе таких материалов возникают специфические проблемы, которые мы обсудим ниже.
Модуль объемной упругости
Модуль объемной упругости, K, определяет изменение объема при заданном равномерном сдавливании. Выраженный через E и nu, он запишется в виде:
K = frac{E}{3(1-2nu)}
Когда nu= 1/3, значение модуля объемной упругости равно значению модуля Юнга, но для несжимаемого материала (nu to0.5), K стремится к бесконечности.
Модуль объемной упругости обычно задается вместе с модулем сдвига. Эти две величины являются, в некотором смысле, более физически независимыми параметрами. Изменение объема материала определяется только модулем объемной упругости, тогда как искажение его формы — только модулем сдвига.
Параметры Ламе
Параметры Ламе́ (коэффициенты Ламе, константы Ламе, постоянные Ламе, упругие постоянные Ламе, модули упругости Ламе) mu и lambda в основном используются для математического описания явлений упругости. Полная система 3-х мерных материальных соотношений между тензором напряжений boldsymbol sigma и тензором деформаций boldsymbol varepsilon (в случае однородной изотропной упругой среды) может быть записана в компактной форме с помощью параметров Ламе в виде:
boldsymbol sigma=2mu boldsymbol varepsilon +lambda ; mathrm{trace}(boldsymbol{varepsilon}) mathbf I
Параметр mu является просто модулем сдвига, тогда как параметр lambda может быть представлен как
lambda = frac{E nu}{(1+nu)(1-2nu)}
Полную таблицу преобразований между различными упругими параметрами можно посмотреть здесь.
Несжимаемость линейных упругих материалов
Некоторые материалы, такие как, например, резина, являются практически несжимаемыми. С математической точки зрения полностью несжимаемый материал принципиально отличается от сжимаемого. В силу того, что отсутствует изменение объема, теперь не представляется возможным определить среднее напряжение. Уравнения состояния для среднего напряжения (давления), p, как функции изменения объема, Delta V, в виде
p = f(Delta V)
более не существует, и вместо этого оно должно быть заменено на ограничение, констатирующее, что
Delta V = 0
Другой подход к проблеме несжимаемости следует из факта, что член (1-2nu) появляется в знаменателе материальных уравнений, так что деление на ноль может произойти только при условии nu= 0.5. Не попробовать ли, в таком случае, смоделировать несжимаемый материал приблизительно, установив значение nu= 0.499?
Это можно сделать, но в данном случае, стандартное смещение узлов сетки, полученное на основе формализма метода конечных элементов, может привести к неожиданным результатам. Это вызвано явлением, называемым блокирование. Возможные эффекты:
- чрезмерно жесткие модели;
- «шахматная» картина напряжений;
- сообщения об ошибках или предупреждения от решателя о плохой обусловленности системы уравнений.
Коррекция результатов возможна при использовании смешанной формулировки, в которой давление вводится в качестве дополнительной степени свободы. В среде COMSOL Multiphysics, включить смешанную формулировку можно, выбрав пункт Почти несжимаемый материал в настройках модели материала.
Часть настроек модели линейного упругого материала, с включенной поддержкой смешанной формулировки.
При величине коэффициента Пуассона большей, чем 0,45 (но, естественно, не большей 0,5), или когда модуль объемной упругости более чем на порядок превышает модуль сдвига, целесообразно использовать смешанную формулировку. Эффект от ее использования показан на рисунке ниже.
Распределение напряжений в простой модели плоских деформаций, nu = 0.499. Верхнее изображение показывает решение, основанное на стандартной формулировке, тогда как нижнее относится к смешанной формулировке.
В решении, использующем в качестве степеней свободы только смещения узлов, картина распределения напряжений обнаруживает искажения в левой части, где имеется ограничение. Эти искажения практически полностью устраняются при использовании смешанной формулировки.
Ортотропия и анизотропия
В общем случае свойства линейных упругих материалов зависят от направления. В наиболее общем случае анизотропного материала это означает, что все шесть компонент тензора напряжений могут зависеть от всех шести компонент тензора деформации. Для описания этого требуется 21 материальный параметр. Ясно, что получение всех этих данных в эксперименте является очень непростой задачей. Если напряжение, boldsymbol sigma, и деформацию, boldsymbolvarepsilon, трактовать как 6-ти мерные векторы (по числу независимых компонент тензора), они будут связаны между собой посредством 6х6 симметричной матрицы материальных параметров mathbf D
boldsymbol sigma= mathbf D boldsymbol varepsilon
К счастью, как правило, неизотропные материалы обладают определенной симметрией. В частном случае ортотропного материала, есть три выделенных ортогональных направления, в которых сдвиг отделяется от осевого действия. То есть, растягивание материала вдоль одного из этих главных направлений, приведет только сжатию (без сдвига) в двух других ортогональных направлениях. Полное описание ортотропного материала требует девяти независимых материальных параметров.
Материальные соотношения в ортотропном материале легче воспринимаются, когда они записаны в виде матрицы податливости (обратной к матрице упругих модулей), boldsymbol varepsilon= mathbf C boldsymbol sigma:
mathsf{C} =
begin{bmatrix}
tfrac{1}{E_{rm X}} & -tfrac{nu_{rm YX}}{E_{rm Y}} & -tfrac{nu_{rm ZX}}{E_{rm Z}} & 0 & 0 & 0 \
-tfrac{nu_{rm XY}}{E_{rm X}} & tfrac{1}{E_{rm Y}} & -tfrac{nu_{rm ZY}}{E_{rm Z}} & 0 & 0 & 0 \
-tfrac{nu_{rm XZ}}{E_{rm X}} & -tfrac{nu_{rm YZ}}{E_{rm Y}} & tfrac{1}{E_{rm Z}} & 0 & 0 & 0 \
0 & 0 & 0 & tfrac{1}{G_{rm YZ}} & 0 & 0 \
0 & 0 & 0 & 0 & tfrac{1}{G_{rm ZX}} & 0 \
0 & 0 & 0 & 0 & 0 & tfrac{1}{G_{rm XY}} \
end{bmatrix}
Поскольку матрица податливости должна быть симметричной, то двенадцать независимых используемых параметров (ненулевых компонентов) сокращаются до девяти, с помощью трех соотношений симметрии типа
tfrac{nu_{rm YX}}{E_Y} = tfrac{nu_{rm XY }}{E_X}
Обратите внимание, что nu_{rm YX} neq nu_{rm XY}, поэтому при работе с ортотропными данными необходимо быть уверенным в том, что используется значение нужного коэффициента Пуассона. В разных источниках обозначения и, соответственно, значения могут различаться.
Анизотропия и ортотропия обычно возникают в неоднородных материалах. Зачастую эти свойства не измеряются, а вычисляются с помощью процесса гомогенизации, когда микроскопические свойства масштабируются до макроскопического уровня. (Суть процесса заключается в усреднении микроскопических уравнений — уравнений, описывающих поведение и свойства одной микрочастицы — по макроскопическому объему, выявляя и сохраняя при этом свойства, которые характеризуют, как индивидуальную микрочастицу, так и весь ансамбль микрочастиц в целом.) Обсуждение такой гомогенизации, правда в несколько ином контексте, можно найти в данной блог-статье.
Для неизотропных материалов имеются ограничения на допустимые значения материальных параметров, аналогичные описанным для изотропных материалов. Затруднительно в явном виде продемонстрировать эти ограничения, но есть две вещи, на которые стоит обратить внимание:
- матрица материальных параметров mathbf D должна быть положительно определенной;
- для произвольного анизотропного материала достаточно проверить, что все собственные значения матрицы положительно определенные величины;
- для ортотропного материала это справедливо, если все шесть упругих модулей положительны, и выполняется неравенство nu_{rm XY}nu_{rm YX}+nu_{rm YZ}nu_{rm ZY}+nu_{rm ZX}nu_{rm XZ}+nu_{rm YX}nu_{rm ZY}nu_{rm XZ}<1
- если материал обладает низкой сжимаемостью, то необходимо применять смешанную формулировку;
- для этого можно оценить эффективный модуль объемной упругости и сравнить со значениями модулей сдвига;
- в случае неопределенности лучше перестраховаться и затратить лишние ресурсы на смешанную формулировку, чтобы избежать возможных неточностей.
Геометрическая нелинейность
При решении геометрически нелинейных задач значение термина “линейная упругость” в действительности является вопросом соглашения. Проблема состоит в том, что существует несколько возможных представлений для описания напряжений и деформаций. Обсуждению различных мер деформаций и напряжений посвящена предыдущая блог-статья.
Так как в качестве исходных величин напряжений и деформаций в среде COMSOL Multiphysics приняты второй тензор напряжений Пиола-Кирхгофа и тензор меры деформации Грина-Лагранжа, то естественное свойство линейной упругости состоит в том, что эти величины имеют линейную зависимость друг относительно друга. Такой материал иногда называют материалом Сен-Венана.
Интуитивно можно предположить, что термин “линейная упругость” означает существование линейной зависимости между прикладываемой силой и смещением в простом эксперименте по растяжению. Однако это не так, поскольку и напряжения, и деформации изменяются по мере растяжения. Чтобы показать это, рассмотрим стержень с квадратным поперечным сечением.
Стержень, подвергнутый равномерному растяжению.
Исходная длина стрежня равна L_0, и первоначальная площадь поперечного сечения составляет A_0=a_0^2, где a_0 — сторона начального сечения. Предположим, что стержень удлиняется на величину Delta, так что текущая его длина составляет L=L_0+Delta=L_0(1+xi)
Здесь 1+xi — это осевое растяжение и xi можно рассматривать как относительное удлинение. Новая длина стороны в поперечном сечении будет равна a=a_0+d=a_0(1+eta), где eta — относительное удлинение в поперечном направлении.
Сила может быть выражена через составляющую тензора напряжения Коши sigma_x в осевом направлении, помноженную на текущую площадь поперечного сечения:
F = sigma_x A = sigma_x A_0 (1+eta)^2
Чтобы использовать линейную упругую зависимость тензоров напряжения и деформации, тензор напряжение Коши boldsymbol sigma необходимо выразить через второй тензор напряжения Пиола-Кирхгофа mathbf S с помощью преобразования вида
mathbf sigma = J^{-1} mathbf F mathbf S mathbf F^T
где mathbf F — тензор градиента деформации, а масштабирование объема определяется J = det(mathbf F) якобианом перехода из одной системы координат в другую. Опуская детали, для одноосного случая получим
sigma_x = frac{F_{xX}}{F_{yY}F_{zZ}}S_X= frac{(1+xi)}{(1+eta)^2}S_X
Так как для материала Сен-Венана при одноосном растяжении осевое напряжение связано с осевой деформацией как S_X = E epsilon_X, получаем
F = S_x A_0 (1+xi) = E A_0 (1+xi)varepsilon_X
С учетом того, что осевой член тензора деформации Грина-Лагранжа определяется выражением
varepsilon_X = frac{partial u}{partial X} + frac{1}{2}(frac{partial u}{partial X})^2 = xi+frac{1}{2}xi^2
выражение для силы в зависимости от смещения преобразуется к виду
F = E A_0 (1+xi)(xi + frac{1}{2}xi^2)=E A_0 (xi+frac{3}{2}xi^2+frac{1}{2}xi^3)
Мы видим, что с учетом геометрической нелинейности линейный упругий материал в действительности подразумевает кубическую зависимость между силой и относительным удлинением (или силы от смещения, поскольку Delta =L_0xi), как показано на рисунке ниже.
Одноосный отклик линейного упругого материала, обусловленный геометрической нелинейностью.
Как видно из графика, жесткость материала стремится к нулю со стороны сжатия, xi = sqrt{{1}/{3}}-1 approx -0.42. На практике это означает, что моделирование при такой степени деформации будет бессмысленным. На самом деле это не является проблемой, так как можно смело утверждать, что не существует реальных материалов, которые остаются линейными при таких больших деформациях. Однако модели линейных упругих материалов зачастую используются далеко за пределами разумного диапазона напряжений по нескольким причинам, среди которых можно выделить следующие:
- часто требуется быстро оценить что-нибудь «по порядку величины», прежде чем использовать более сложную модель материалов;
- в модели есть сингулярности, которые вызывают очень высокие деформации в некоторых точках;
- более подробно о сингулярностях можно посмотреть здесь.
- в исследовании контактных задач всегда проявляется геометрическая нелинейность;
- зачастую в ходе анализа высокий уровень сжимающих напряжений (а, следовательно, и деформаций) появляется локально на какое-то время в зоне соприкосновения материалов.
Во всех этих случаях решатель может не найти решения, если деформации сжатия становятся слишком большими. Если вы подозреваете, что столкнулись с такой ситуацией, то хорошей идеей будет графическое построение наименьшего главного значения тензора деформации. Если оно меньше, чем -0,3 или около того, то можно ожидать такого рода сбой при моделировании. Критическим значением, в терминах деформации по Грину-Лагранжу, является -1/3. Если проблема заключается в этом, то следует рассмотреть возможность замены модели на подходящую модель гиперупругого материала.
Сжатие — это не единственная проблема. В приведенном выше анализе коэффициент Пуассона не входил в уравнения. Так что же, на самом деле, происходит с поперечным сечением?
По определению, в одноосном случае поперечная деформация связана с осевой посредством отношения
varepsilon_Y = -nu varepsilon_X
Поскольку эти деформации являются компонентами тензора деформаций Грина-Лагранжа, значит они подчиняются нелинейным выражениям
frac{partial v}{partial Y} + frac{1}{2}(frac{partial v}{partial Y})^2 = -nu (frac{partial u}{partial X} + frac{1}{2}(frac{partial u}{partial X})^2)
Таким образом, при деформации имеется сильная нелинейная зависимость в изменении поперечного сечения. Решение этого квадратного уравнения приводит к следующему соотношению между поперечной и продольной деформациями
eta = sqrt{1-nu(xi^2+2xi)}-1
Результат показан на рисунке ниже.
Поперечное смещение как функция осевого смещения для одноосного растяжения материала Сен-Венана. Показаны зависимости для пяти различных значений коэффициента Пуассона.
Как видно, поперечное сечение быстро сжимается при больших растяжениях с ростом значений коэффициента Пуассона.
Если бы был выбран другой способ представления напряжения и деформации, например, если бы тензор напряжения Коши был пропорционален логарифмической, или “истинной” деформации, то это привело бы, скорее всего, к совсем другому результату. Такой материал имеет жесткость, которая, напротив, уменьшается при удлинении, когда связь между силой и смещением определяется значением коэффициента Пуассона. Тем не менее, оба материала можно корректно называть “линейно упругими”, хотя результаты вычислений для больших упругих деформаций в рамках двух различных платформ моделирования могут сильно различаться между собой.
Заключительные замечания по линейным упругим материалам
Мы проиллюстрировали некоторые ограничения на использование линейных упругих материалов. В частности, указали на возможные подводные камни, связанные с несжимаемостью, и комбинацией линейной упругости с большими деформациями.
Для интересующихся вопросами моделирования материалов в строительной механике и механике сплошных сред рекомендуем ознакомиться со следующими блог-статьями:
- Введение в нелинейные упругие материалы (Introducing Nonlinear Elastic Materials)
- Экспериментальное получение параметров материала для строительной механики (Obtaining Material Data for Structural Mechanics from Measurements)
- Часть 2: Экспериментальное получение параметров материала для строительной механики (Part 2: Obtaining Material Data for Structural Mechanics from Measurements)
- Подгонка параметров различных моделей гиперупругих материалов для соответствия экспериментальным данным (Fitting Measured Data to Different Hyperelastic Material Models)
- Текучесть поверхности и законы пластического течения в геомеханике (Yield Surfaces and Plastic Flow Rules in Geomechanics)
- Вычисление жесткости линейных упругих конструкций: Часть 1 (Computing Stiffness of Linear Elastic Structures: Part 1)
- Вычисление жесткости линейных упругих конструкций: Часть 2 (Computing Stiffness of Linear Elastic Structures: Part 2)
Источник
Диаграммы напряжений
На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.
Тут может возникнуть вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления некоторого предела — сопротивления, существуют только в теории. В реальности большинство материалов обладают как упругими так и пластическими свойствами, что это за свойства, рассмотрим ниже на примере металлов.
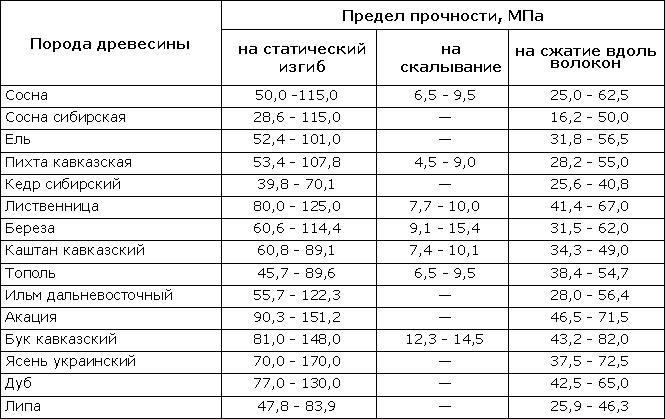
Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.
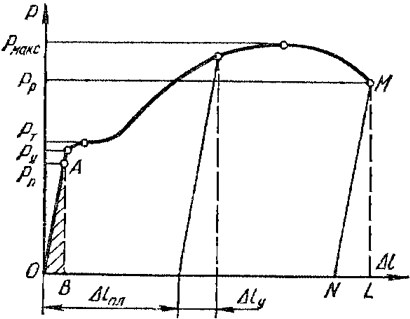
Рисунок 318.1. Диаграмма напряжений для стального образца.
На данной диаграмме мы видим 5 характерных точек:
1. Предел пропорциональности Рп (точка А)
Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:
σп = Рп/Fo (318.2.1)
Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:
Рп = kΔl (318.2.2)
где k — коэффициент жесткости:
k = EF/l (318.2.3)
где l — длина образца, F — площадь сечения, Е — модуль Юнга.
Модули упругости
Главными характеристиками упругих свойств материалов являются модуль Юнга Е (модуль упругости первого рода, модуль упругости при растяжении), модуль упругости второго рода G (модуль упругости при сдвиге) и коэффициент Пуассона μ (коэффициент поперечной деформации).
Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности
Модуль Юнга также определяется опытным путем при испытании стандартных образцов на растяжение. Так как нормальные напряжения в материале равны силе, деленной на начальную площадь сечения:
σ = Р/Fо (318.3.1), (317.2)
а относительное удлинение ε — отношению абсолютной деформации к начальной длине
εпр = Δl/lo (318.3.2)
то модуль Юнга согласно закону Гука можно выразить так
Е = σ/εпр = Plo/FoΔl = tgα (318.3.3)
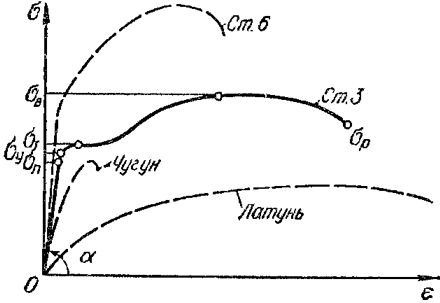
Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов
Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным
Под воздействием нагрузок не только увеличивается длина образца, но и уменьшается площадь рассматриваемого поперечного сечения (если предположить, что объем материала в области упругих деформаций остается постоянным, то значит увеличение длины образца приводит к уменьшению площади сечения). Для образца, имеющего круглое сечение, изменение площади сечения можно выразить так:
εпоп = Δd/do (318.3.4)
Тогда коэффициент Пуассона можно выразить следующим уравнением:
μ = εпоп/εпр (318.3.5)
Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига
Модуль сдвига G может быть определен опытным путем при испытании образцов на кручение.
При угловых деформациях рассматриваемое сечение перемещается не линейно, а под некоторым углом — углом сдвига γ к начальному сечению. Так как касательные напряжения равны силе, деленной на площадь в плоскости которой действует сила:
т = Р/F (318.3.6)
а тангенс угла наклона можно выразить отношением абсолютной деформации Δl к расстоянию h от места фиксации абсолютной деформации до точки, относительно которой осуществлялся поворот:
tgγ = Δl/h (318.3.7)
то при малых значениях угла сдвига модуль сдвига можно выразить следующим уравнением:
G = т/γ = Ph/FΔl (318.3.8)
Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны между собой следующим отношением:
Е = 2(1 + μ)G (318.3.9)
Значения постоянных Е, G и µ приводятся в таблице 318.1
Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов
Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления различных строительных материалов меняются и более точные значения модулей упругости следует уточнять по действующим в настоящий момент нормативным документам. Модули упругости бетона зависят от класса бетона и потому здесь не приводятся.
Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. Между тем на диаграмме напряжений можно выделить еще несколько точек:
2. Предел упругости Ру
Нормальные напряжения в поперечном сечении образца при достижении предела упругости будут равны:
σу = Ру/Fo (318.2.4)
Предел упругости ограничивает участок на котором появляющиеся пластические деформации находятся в пределах некоторой малой величины, нормированной техническими условиями (например 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается соответственно допуску σ0.001, σ0.01 и т.д.
3. Предел текучести Рт
σт = Рт/Fo (318.2.5)
Ограничивает участок диаграммы на котором деформация увеличивается без значительного увеличения нагрузки (состояние текучести). При этом по всему объему образца происходит частичный разрыв внутренних связей, что и проводит к значительным пластическим деформациям. Материал образца полностью не разрушается, но его начальные геометрические размеры претерпевают необратимые изменения. На отшлифованной поверхности образцов наблюдаются фигуры текучести — линии сдвигов (открытые профессором В. Д. Черновым). Для различных металлов углы наклона этих линий различны, но находятся в пределах 40-50о. При этом часть накопленной потенциальной энергии необратимо расходуется на частичный разрыв внутренних связей. При испытании на растяжение принято различать верхний и нижний пределы текучести — соответственно наибольшее и наименьшее из напряжений, при которых возрастает пластическая (остаточная) деформация при почти постоянной величине действующей нагрузки.
На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.
Некоторые материалы не имеют выраженной площадки текучести. Для них за условный предел текучести σ0.2 принимается напряжение, при котором остаточное удлинение образца достигает значения ε ≈0,2%.
4. Предел прочности Рмакс (временное сопротивление)
Нормальные напряжения в поперечном сечении образца при достижении предела прочности будут равны:
σв = Рмакс/Fo (318.2.6)
После преодоления верхнего предела текучести (на диаграммах напряжения не показан) материал снова начинает сопротивляться нагрузкам. При максимальном усилии Рмакс начинается полное разрушение внутренних связей материала. При этом пластические деформации концентрируются в одном месте, образуя в образце так называемую шейку.
Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.
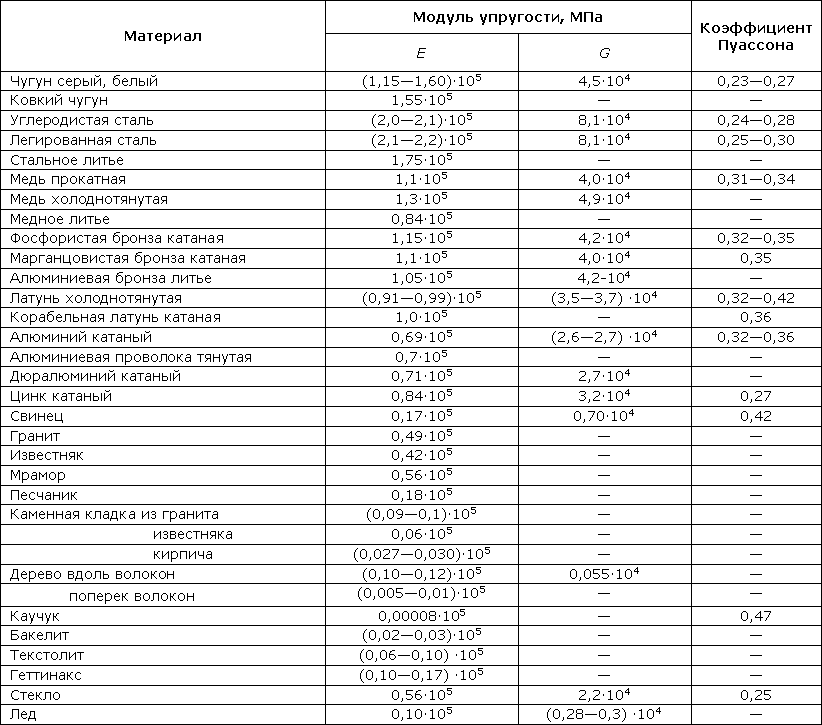
В таблицах 318.2 — 318.5 приведены ориентировочные величины пределов прочности для некоторых материалов:
Таблица 318.2 Ориентировочные пределы прочности на сжатие (временные сопротивления) некоторых строительных материалов.

Примечание: Для металлов и сплавов значение пределов прочности следует определять согласно нормативных документов. Значение временных сопротивлений для некоторых марок стали можно посмотреть здесь.
Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для некоторых пластмасс

Таблица 318.4. Ориентировочные пределы прочности для некоторых волокон
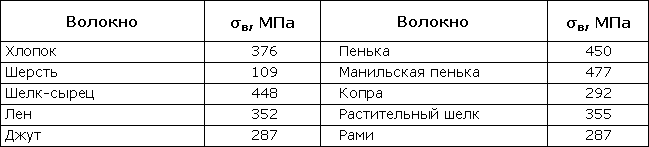
Таблица 318.5. Ориентировочные пределы прочности для некоторых древесных пород

5. Разрушение материала Рр
Если посмотреть на диаграмму напряжений, то создается впечатление, что разрушение материала наступает при уменьшении нагрузки. Такое впечатление создается потому, что в результате образования «шейки» значительно изменяется площадь сечения образца в районе «шейки». Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, то будет видно, что напряжения в рассматриваемом сечении увеличиваются до некоторого предела:
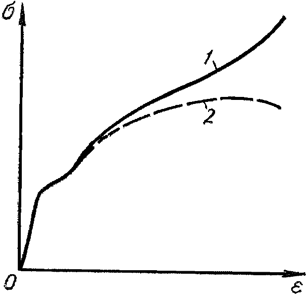
Рисунок 318.3. Диаграмма напряжений: 2 — по отношению к начальной площади поперечного сечения, 1 — по отношению к изменяющейся площади сечения в районе шейки.
Тем не менее более правильным является рассмотрение прочностных характеристик материала по отношению к площади первоначального сечения, так как расчетами на прочность изменение первоначальной геометрической формы редко предусматривается.
Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:
ψ = 100(Fo — F)/Fo (318.2.7)
где Fo — начальная площадь поперечного сечения образца (площадь поперечного сечения до деформации), F — площадь поперечного сечения в районе «шейки». Чем больше значение ψ, тем более ярко выражены пластические свойства материала. Чем меньше значение ψ, тем больше хрупкость материала.
Если сложить разорванные части образца и измерить его удлинение, то выяснится, что оно меньше удлинения на диаграмме (на длину отрезка NL), так как после разрыва упругие деформации исчезают и остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.
За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 некоторая точка между пределом текучести и пределом прочности), и затем разгрузить его, то в образце останутся пластические деформации, но при повторном загружении через некоторое время предел упругости станет выше, так как в данном случае изменение геометрической формы образца в результате пластических деформаций становится как бы результатом действия внутренних связей, а изменившаяся геометрическая форма, становится начальной. Этот процесс загрузки и разгрузки материала можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:

Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям)
Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Тем не менее при повышении прочности металла путем наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому полезным как правило считается относительно небольшой наклеп.
Работа деформации
Прочность материала тем выше, чем больше внутренние силы взаимодействия частиц материала. Поэтому величина сопротивления удлинению, отнесенная к единице объема материала, может служить характеристикой его прочности. В этом случае предел прочности не является исчерпывающей характеристикой прочностных свойств данного материала, так как он характеризует только поперечные сечения. При разрыве разрушаются взаимосвязи по всей площади сечения, а при сдвигах, которые происходят при всякой пластической деформации, разрушаются только местные взаимосвязи. На разрушение этих связей затрачивается определенная работа внутренних сил взаимодействия, которая равна работе внешних сил, затрачиваемой на перемещения:
А = РΔl/2 (318.4.1)
где 1/2 — результат статического действия нагрузки, возрастающей от 0 до Р в момент ее приложения (среднее значение (0 + Р)/2)
При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение:
А = ηРмаксΔlмакс (318.4.2)
где η — коэффициент полноты диаграммы, равный отношению площади всей диаграммы, ограниченной кривой АМ и прямыми ОА, MN и ON, к площади прямоугольника со сторонами 0Рмакс (по оси Р) и Δlмакс (пунктир на рис. 318.1). При этом надо вычесть работу, определяемую площадью треугольника MNL (относящуюся к упругим деформациям).
Работа, затрачиваемая на пластические деформации и разрушение образца, является одной из важных характеристик материала, определяющих степень его хрупкости.
Деформация сжатия
Деформации сжатия подобны деформациям растяжения: сначала происходят упругие деформации, к которым за пределом упругости добавляются пластические. Характер деформации и разрушения при сжатии показан на рис. 318.5:

Рисунок 318.5
а — для пластических материалов; б — для хрупких материалов ; в — для дерева вдоль волокон, г — для дерева поперек волокон.
Испытания на сжатие менее удобны для определения механических свойств пластических материалов из-за трудности фиксирования момента разрушения. Методы механических испытаний металлов регламентируются ГОСТ 25.503-97. При испытании на сжатие формы образца и его размеры могут быть различными. Ориентировочные значения пределов прочности для различных материалов приведены в таблицах 318.2 — 318.5.
Если материал находится под нагрузкой при постоянном напряжении, то к практически мгновенной упругой деформации постепенно прибавляется добавочная упругая деформация. При полном снятии нагрузки упругая деформация уменьшается пропорционально уменьшающимся напряжениям, а добавочная упругая деформация исчезает медленнее.
Образовавшаяся добавочная упругая деформация при постоянном напряжении, которая исчезает не сразу после разгрузки, называется упругим последействием.
Влияние температуры на изменение механических свойств материалов
Твердое состояние — не единственное агрегатное состояние вещества. Твердые тела существуют только в определенном интервале температур и давлений. Повышение температуры приводит к фазовому переходу из твердого состояния в жидкое, а сам процесс перехода называется плавлением. Температуры плавления, как и другие физические характеристики материалов, зависят от множества факторов и также определяются опытным путем.
Таблица 318.6. Температуры плавления некоторых веществ
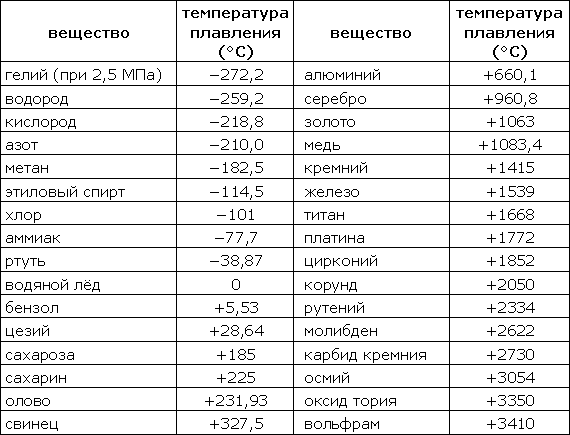
Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).
Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20оС. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35оС.
При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σп, σт и σв) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.
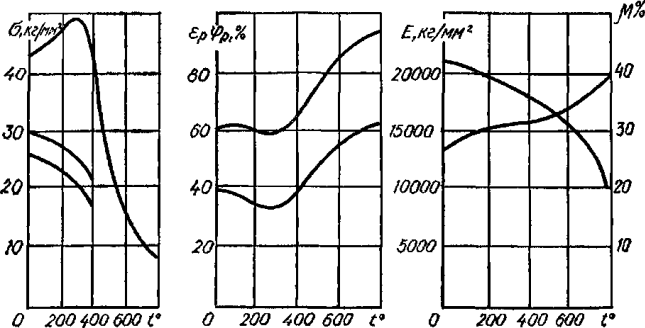
Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.
При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σв1100 = 2σв20.
Характе
