Как найти упругое растяжение

Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Механика
Силы в природе
1.12. Сила упругости. Закон Гука
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
| Рисунок 1.12.1. Деформация растяжения ( x > 0 ) и сжатия ( x < 0 ). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
| Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.
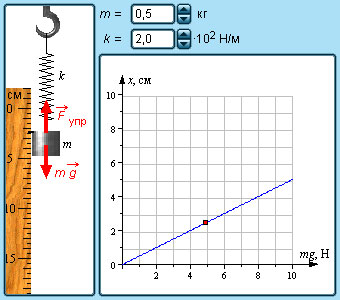
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
 |
Модель. |
Источник
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Электрокапиллярные явления отражают зависимость пограничного натяжения на границе электрод — раствор от потенциала электрода и состава раствора. Для жидких металлов (ртуть, галлий, амальгамы, расплавы) пограничное натяжение у совпадает с обратимой поверхностной работой а и может быть экспериментально измерено, так как жидкая граница раздела допускает изменение ее поверхности в обратимых условиях (достаточно, например, наклонить стаканчик со ртутью, покрытой раствором, чтобы изменилась поверхность ртутного электрода). С другой стороны, даже небольшое упругое растяжение твердого электрода приводит к увеличению расстояния между атомами металла на поверхности, а следовательно, растянутая поверхность не идентична первоначальной и имеет иное значение о. Если при упругом растяжении площадь поверхности увеличилась на с15, то затраченная на растяжение работа равна [c.171]
При положительной магнитострикции направление упругого растяжения является направлением легкого намагничивания, если работа, рас- [c.53]
Влияние упругого растяжения при условии пропускания тока вдоль действующей силы вычисляется ш формулы [c.57]
Проведем небольшой опыт. Увеличим поверхность тела, сохранив его объем. Однако расстояние между молекулами не увеличится, упругого растяжения не произойдет. Молекулы жидкости из объема перейдут на ее поверхность, образуя поверхностный слой толщиной в одну молекулу — мономолекулярный слой. Пусть молекулы будут упакованы в поверхностном слое в виде кубиков одинакового размера с ребром Ь длиной 3—5 А (1А = 10 см). Тогда площадь, занятая одной молекулой (Ь ), будет равна 10—25 а молекул на I см [c.22]
Для осуществления подобного механизма упругого растяжения необходим ряд условий, которые наиболее полно осуществляются именно в молекуле каучука и его аналогов, чем и объясняется, почему именно они, а не все соединения с нитевидными молекулами обладают каучукоподобной упругостью. Прежде всего необходимо, чтобы молекулы были достаточно гибкими, способными легко принимать самые различные формы. Такого рода гибкая молекула должна содержать в качестве боковых отростков по возможности малые группы (в природном каучуке метильная группа). Тем самым становится понятно, почему, например, такое вещество, как полистирол (боковая цепь — фенил), обладает значительно меньшей упругостью, чем природный каучук. [c.322]
Далее необходимо, чтобы межмолекулярные силы были и не слишком малы, и не слишком велики. При слишком малом меж-молекулярном взаимодействии молекулы свободно отрывались бы друг от друга и вместо упругого растяжения наблюдалось бы течение, как у жидкостей или смол. Слишком большие межмолекулярные силы препятствовали бы скольжению молекул и их ориентировке под действием растягивающей силы. Поэтому, например, такое вещество, как клетчатка, не обладает значительной упругостью. Между нитевидными молекулами клетчатки (которые к тому же обладают меньшей гибкостью, чем тонкие молекулы поли-изопреноидов) действуют значительные межмолекулярные силы, прежде всего в виде водородных связей между ОН-группами, входящими в состав разных цепей. Можно вообще предвидеть, что присутствие в макромолекуле полярных групп, сильно увеличивающих взаимодействие между молекулами, должно приводить к уменьшению упругого растяжения. [c.322]
Пределы прочности на растяжение на сжатие на изгиб Модуль упругости (растяжение) Твердость [c.73]
Для капронового волокна теоретическая прочность оказалась меньше технической. Этот физически неоправданный результат свидетельствует о том, что формулами для расчета теоретической прочности твердых тел следует пользоваться с осторожностью, если речь идет о полимерах. Причина этого, по-видимому, заключается в том, что модуль упругости твердых полимеров в основном определяется межмолекулярным взаимодействием (модуль же упругого растяжения отдельной полимерной цепи на один-два порядка больше), а прочность—химическими связями. [c.15]
Механизм упругой деформации заключается в увеличении средних расстояний между атомами и молекулами, а в случае полимеров он сводится к изменению длин связей и деформации валентных углов. Упругая деформация сопровождается изменением объема тела под действием внешнего напряжения и развитие ее связано с изменением потенциальной энергии системы. Вследствие этого твердое тело поглощает тепло (охлаждается) при упругом растяжении и выделяет его при сжатии. При высокоэластической деформации аморфных полимеров объем образца, как правило, не меняется. Высокоэластическая деформация во многих случаях практически не сказывается на изменении потенциальной энергии системы. При этом образец при растяжении нагревается, а сокращаясь, поглощает такое же количество тепла. [c.75]
На основании приведенных данных нам кажется, что процесс ориентации целлюлозного волокна при его растяжении представляет собой процесс упругого растяжения, подобно процессу растяжения каучука. Скорость [c.26]
Анализ полученных данных показал, что при упругом растяжении общий характер НМС практически не меняется, но происходят заметные изменения значений параметров микрофибриллярной структуры. В области малых углов максимум смещается, в соответствии с увеличением Ь. Помимо этого в несколько раз увеличивается интенсивность рефлекса. Оба явления обратимы — после разгружения (и восстановления исходной длины образца) малоугловой рефлекс по интенсивности и угловому положению возвращается к исходному. [c.138]
При упругом растяжении полимеров продольный размер кристаллитов вдоль цепи остается, как отмечают авторы [c.141]
Особенности поведения ориентированных образцов ИПП под нагрузкой в интервале от —30 до 50 °С и ПКА в условиях циклического нагружения рассмотрены в работах [139, 140], а поведение отожженных ориентированных образцов ПЭ — в работе [141]. Непосредственно установлено, что кинетическая гибкость полимерных цепей может изменяться не только в зависимости от температуры, но и в силу как бы механического стеклования аморфных областей полимера. Анализ этих данных показал, что торможение сегментального движения в напряженном состоянии следует объяснять уменьшением числа возможных конформаций цепей при растяжении, а не увеличением стерических межмолекулярных препятствий движению [142, 143]. Торможение молекулярного движения означает, что под нагрузкой полимер теряет эластические свойства — в момент разрыва материал ближе к твердому телу, чем в исходном состоянии. Таким образом, как ИК-спектроскопические, так и ЯМР-данные свидетельствуют о гош-гранс-иереходах, возникающих при упругом растяжении ориентированных аморфно-кристаллических полимеров. [c.145]
Однако при упругом растяжении или при дальнейшем увеличении степени вытяжки гранс-участки [c.155]
Опыт показывает, что упругости растяжения и изгиба Н-связи примерно пропорциональны ее энергии [26—281. Взаимосвязь энергии с эквивалентными кх величинами и Атон рассмотрена ниже, в разделе 2.2. Менее точная, ориентировочная, но весьма широкая пропорциональность [c.117]
Модуль нормальной упругости растяжения отожженного бария Е в завнсимости от температуры [c.119]
Затяжка гаек с приложением крутящего момента имеет ряд недостатков, в том числе необходимость преодоления значительных сил трения. Этот недостаток устраняется при использовании гидравлических теисеров — устройств для упругого растяжения болта (шпильки). Гидротенсер состоит из резьбовой втулки для захвата резьбового конца шпильки, упорной втулки, гидро-114 [c.114]
При упругом растяжении или кручении увеличиваются межатомные расстояния, и электрическое сопрогавленне металлов возрастает. [c.57]
Наиболее наглядно влияние упругих напряжений на магнитную доменную структуру многоосных ферромагнетиков с различной кристаллографической ориентацией поверхности видно на магнитотрехосных кристаллитах железокремнистых сталей, обладающих положительной магни-тостриктщей [87]. Одноосные упругие деформации приводят к существенной перестройке типа магнитной структуры (переход от 90 к 180°), изменяют размеры отдельных доменов и вид междоменных фаниц. Поскольку материал имеет положительную магнитострикцию, действие продольных упругих растяжений в кристалле Ре — 3 % 81 типа (100) приводит к уменьшению объемов всех доменов с поперечной (относительно (Зо) ориентацией намагниченности (рисунок 2.2.1, домены А, В, С и В). [c.59]
Существенные изменения вида доменов и их размерных параметров вызьгаают и плоскостные (или двухосные) упругие растяжения [83]. На рисунке 2.2.4 можно видеть значительное изменение ширины полосовых доменов в кристалле идеальной ориентации (угол = 0) в направлении [001] (рисунок 2.2.4, а — в). [c.62]
Таким образом, действие растяжения приводит к перестройке доменной структуры железа и наводит одноосную магнитную анизотропию за счет активных смещений 180° и 90° междоменных фаниц. При этом формируется одноосная магнитная текстура в железе, ось которой совпадает с осью образца. Поэтому упругое растяжение в железе формирует систему больших по длине продольных полосовых доменов. Число этих доменов значительно увеличивается гфи тшастической деформации за счет возникновения и роста клиновидных областей вблизи протяженных дефектов. [c.65]
Рассмотрим термодинамическую трактовку деформапионной активации металла, применимую для упругих дефорМашш металла в вершине трещины. Известно, что для упругого растяжения стержня деформационный сдвиг в отрицательную сторону равновесного электродного потенциала А р описывается уравнением, приведенным в [15] [c.69]
Учить1вая, что отвод ионов металла из трещины затруднен и концентрация их там повышена, допускаем, что локальный (при отсутствии короткого замыкания цепи) потенциал металла в вершине трещины близок к равновесному. Подставляя значение Д из уравнения (7) в уравнение (3) вместо ДЁ ,, т. е. принимая деформационный сдвиг равновесного потенциала равным ЭД.С. коррозионного элемента (вершина зародышевой трещины — ее стенки), получим выражение скорости к, подрастания трещины при упругом растяжении образца (детали), ослабленным данной трещиной [c.69]
Живица представляет собой вязкую и липкую жидкость, перемещение которой по каналам смоляных ходов сопряжено с большими силовыми затратами. Механизм выделения живицы на срезе объясняется действием осмотического и секреторного давления, а также сосущей силой транспирационных токов. Образуемая в клетках эпителия живица выделяется в канал смоляного хода под действием секреторного давления этих клеток, которое при закрытом смолоходе преодолевает осмотическое давление протопласта и сдавливает выстилающее клетки, вытесняя воду из них в слой мертвых клеток. При открытом смолоходе секреторное давление на выстилающие клетки снижается, они набухают за счет влаги, отсасываемой из окружающих клеток, и находятся в тур горсцирующем состоянии, под которым понимается упругое растяжение их оболочки. [c.196]
В области каучукоподобного состояния Tg Т Tf, кривые 6—8 на рис. I. 11) диаграмма напряжение — деформация имеет S-образную форму. Пологий участок кривой 500 ВОО 700 ш соответствует развитию высокоэластической деформации, которая развивается при постоянном значении растягивающей силы. Поэтому условное напряжение также остается постоянным. Истинное напряжение, рассчитанное с учетом умеиьщения площади поперечного сечения, с увеличением деформации непрерывно растет деформационные кривые в истинных напряжениях имеют вид, представленный на рис. I. 12. Уменьшение крутизны кривой в области перегиба объясняется снижением высокоэластического модуля. Возрастание крутизны конечного участка кривой объясняется тем, что при этих деформациях для большей части макромолекул реализована вся возможная высокоэластическая деформация и дальнейшее растяжение образца вызывает их упругое растяжение. [c.27]
На рис. П. 23, а приведены малоугловые и большеугловые )ентгенограммы для свободного и упруго растянутого образца 1КА, а на рис. 11.23, б — запись с помощью счетчика изменений интенсивности и углового положения дифракционного малоуглового максимума при упругом растяжении ПКА о поведении других полимеров см. [4]. [c.138]
При изучении нагруженных ориентированных ПКА, ПП, ПЭТФ и др. в температурной области, когда их аморфные участки не застеклованы, установлен качественно одинаковый эффект упругого растяжения — амплигуда узкой компоненты спектра уменьшалась и тем сильнее, чем больше был растянут образец. При этом возрастала амплитуда широкой компоненты (рис. П. 25, о., [138]). Влияние растяжения обратимо — после разгрузки полимеров начальная форма их спектров восстанавливалась. Внешне нагрузка вызывала такую же трансформацию спектров, что и понижение температуры. [c.144]
Дополнительными доказательствами в пользу модели Гесса — Херла могут служить волокна из целлюлозы. Для них большинство исследователей всегда принимало очень большое число проходных молекул, хотя многие физические свойства этих волокон близки к свойствам высокоориентированных гибкоцепных полимеров. Выше мы отмечали такие факты, как увеличение продольных размеров кристаллитов при ориентационной вытяжке и упругом растяжении гибкоцепных полимеров (при неизменном поперечном размере микрофибриллы). Кроме того, хорошо известна способность таких полимеров как каучук, гуттаперча и ПЭТФ кристаллизоваться при растяжении из аморфного состояния после достижения зна.чительных степеней вытяжки. Так как для подрастания или возникновения кристаллита определенного поперечного размера необходимо не произвольное число макромолекул, а строго определенное (которое можно найти с учетом параметров элементарных ячеек), нам представляется, что эти факты являются серьезным доводом Б пользу модели Гесса — Херла. [c.151]
Таким образом, эти результаты позволяют утверждать, что разнодлинность отрезков цепей не столь уж велика. Ниже мы увидим, что большому числу сильно изогнутых цепей просто некуда втиснуться, прослойки должны были бы разбухнуть, приобрели бы бочкообразную форму, чего не следует как из ЭМ снимков, так и из данных малоугловой рентгеновской дифракции. Исследования методом ЯМР нагруженных полимеров также показывают, что при упругом растяжении ориентированных полимеров узкая компонента вымораживается уже при удлинениях — 8% для ПВС-волокон и для ПКА. Если бы ориентированные волокна содержали значительное число складок или в них была бы значительная дисперсия длин отрезков макромолекул в неупорядоченных областях, то столь полного механического стеклования вряд ли можно было бы добиться. Все вышеприведенные данные, как нам кажется, позволяют утверждать, что разнодлинность проходных молекул в неупорядоченных областях сравнительно невелика, например, для высокоориентированного ПЭ не более 5—10% [36]. [c.153]
СВЕРХПРОВОДИМОСТЬ — свойство материалов не оказывать сопротивления электрнческому току при температурах ниже характерной для них критической температуры. Материалы, обладающие таким св-вом, наз. сверхпроводящими материалами. Если т-ра ниже критической, удельное электрическое сопротивление сверхпроводника теоретически равно нулю (экспериментально определен лишь верхний предел — пиже 10 ом-см). Магн. индукция массивного сверхпроводника при т-ре ниже критической равна нулю — магн. поле выталкивается из объема материала ири переходе его в сверхпроводящее состояние и остается лишь в тонком поверхностном слое (толщиной 10 —см). Различают сверхпроводники первого рода — чистые металлы и сверхпроводники второго рода — сплавы (однородные, однофазные). Чтобы материал пз сверхпроводящего состояния перешел в нормальное (не сверхпроводящее), его нагревают до т-ры выше критической или повышают (при т-ре ниже критической) напряженность внешнего магн. поля (либо поля протекающего тока) выше определенного критического значения. Критическая напрягкенность внешнего магн. поля растет с понижением т-ры ниже критической и достигает макс. значения при т-ре О К. Если значение напряженности внешнего магн. ноля становится выше критического, сопротивление материала скачкообразно восстанавливается (при. малом коэфф. размагничения), магн. поле проникает в материал. Критические т-ра и напряженность внешнего ноля сверхпроводника зависят от внешнего давления и упругого растяжения. Переход в сверхпроводящее состояние в отсутствие внешнего магн. поля — фазовый переход второго рода, во внешнем магн. поле — фазовый переход первого рода. Сверхпроводники первого рода переходят в сверхпроводящее состояние при определенном значении магп. поля, сверхпроводники второго рода — в широком интервале этих значений. С. обусловлена сверхтекучестью элект- [c.344]
Тем не менее, задача сопряжения концевых деталей и гибких элементов с трубой ротора достаточно сложна по следующей причине. При ускорении вращения ротора и возрастании в его тангенциальной обмотке напряжений пропорционально квадрату окружной скорости диаметр трубы из композитного материала может увеличиться на 1,5%. Однако известные в настоящее время высокопрочные сплавы не обладают способностью в той же степени увеличивать свои размеры при упругом растяжении. Поэтому крышка, плотно вставленная в покоящийся ротор, при его вращении в зоне упругих деформаций будет увеличивать свой диаметр меньше, чем труба, образуя между этими сопряжёнными деталями недопустимый зазор. Разумеется, эта задача существует не только для роторов центрифуг. Так, например, если на быстро вращающийся вал надеть на точной посадке диск существенно большего внешнего диаметра, то его растяжение будет много больше, чем у вала, и посадка прослабится, точность вращения диска будет потеряна. Подобная проблема имеет место в авиационных двигателях, паровых турбинах, мощных газоперекачивающих турбокомпрессорах и т. д. [c.182]
В настоящее время для систематики колебаний ядер широкое применение-нолучили представления, развитые Мекке в 1930 г. На первый взгляд может показаться, что эти представления чрезмерно упрощают вопрос поэтому они способны вызвать к себе некоторое недоверие, однако практика показала, что они вполне приемлемы. Согласно Мекке, химическую связь между двумя атомами внутри молекулы в отношении колебания атомов можно характеризовать двумя константами упругости растяжения и изгиба. Таким образом, валентная связь двух атомов может быть в известной мере уподоблена упругому стержню, который способен испытывать растяжение и изгиб, В соответствии с этим внутримолекулярные колебания ядер друг относительно друга в настоящее время классифицируют на валентные колебания (V-колебания), подразумевая под этим продольные изменения расстояний между ядрами, т. е. как бы растяжение и сжатие упругого стержня, характеризующего собой валентную связь, и деформирующие колебания (б-коле-бания). [c.162]
Рост растений и дифференцировка (1984) — [
c.134
]
Источник
