Как найти растяжение динамометра



Главная 
 Онлайн учебники 
 База репетиторов России 
 Тренажеры по физике 
 Подготовка к ЕГЭ 2017 онлайн

Глава 1. Механика

Силы в природе

1.12. Сила упругости. Закон Гука

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).

При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:

Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:

Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.

Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).

Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.

В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.

В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.

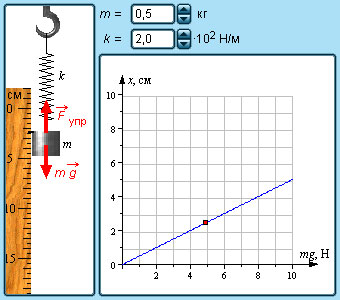Модель. Закон Гука





Сила упругости

Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.

Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.

Определение. Что такое сила упругости?

Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние. 

Рассмотрим простейшие деформации — растяжение и сжатие 

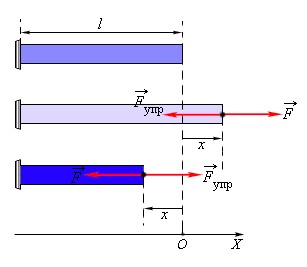
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.

Закон Гука

Для малых деформаций x≪ l справедлив закон Гука. 

Закон Гука

Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS.  Здесь S — площадь поперечного сечения деформированного тела.  Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению. 

ε=σE.

Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2

Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня. 

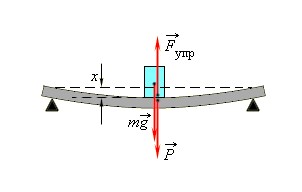
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения. 

Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает. 

Вес тела — это сила, с которой оно действует на опору. 

Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр. 

Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.

При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k). 

В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.

1. Твёрдые тела под действием силы способны изменять свои форму и (или) объём. Взяв за концы металлическую линейку, можно её согнуть. Если перестать прикладывать силу, то линейка восстановит свою форму. Если сжать пружину (рис. 35), то она сократится, т.е. деформируется. При прекращении действия силы пружина вернётся в первоначальное
состояние.

Изменение формы или объёма тела при действии на него силы называется деформацией.

Если длина пружины в недеформированном состоянии ​( l_0 )​, а после растяжения ​( l )​, то изменение её длины ​( l=l-l_0=x )​, где ​( l )​ или ​( x )​ – удлинение или деформация.

2. При деформации в теле возникает сила упругости, которая стремится вернуть его в первоначальное состояние. Сила упругости ​( (vec{F}_{упр}) )​ — сила, возникающая в теле в результате деформации, стремящаяся вернуть тело в первоначальное состояние и направленная в сторону, противоположную деформации (удлинению).

Так, при растяжении пружины эта сила направлена влево к положению равновесия, при
сжатии пружины сила упругости направлена вправо (рис. 36).

Если тело после прекращения действия силы принимает первоначальную форму, то деформация является упругой. Если тело после прекращения действия силы не принимает первоначальную форму, то деформация является неупругой или пластической.

3. При малых деформациях сила упругости прямо пропорциональна удлинению. Поскольку сила упругости и деформация направлены в противоположные стороны, то: ​( F_{упр}=-kDelta l )​, где ​( k )​ — коэффициент пропорциональности, называемый жёсткостью тела. Жёсткость зависит от размеров тела, его формы, материала, из которого сделано тело.

Единица жесткости ​( [,k,]=frac{[,F,]}{[,Delta l,]} )​; ​( [,k,]=frac{1,Н}{1,м}=1frac{Н}{м} )​.

Формула ( F_{упр}=-kDelta l ) выражает закон Гука: сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению (деформации) тела и направлена в сторону, противоположную деформации.

Важно понимать, что закон Гука справедлив при малых деформациях.

На рисунке 37 приведён график зависимости модуля силы упругости от деформации. Поскольку эта зависимость линейная, то графиком зависимости является прямая, проходящая через начало координат и составляющая угол ​( alpha )​ с осью абсцисс. По графику можно определить жёсткость тела. Например, значению деформации 2 см соответствует сила упругости 4 Н. Разделив 4 Н на 0,02 м, получим ​( k )​ = 200 Н/м. В треугольнике АОВ жёсткость ​( k )​ равна тангенсу угла ​( alpha )​: ​( k=mathrm{tg}alpha )​.

4. Существуют разные виды деформации: растяжения, сжатия, сдвига, изгиба и кручения. В рассмотренных примерах линейка подвергалась деформации изгиба, пружина — деформации растяжения и сжатия, винты, гайки, болты при закручивании испытывают деформацию кручения, тяжёлые предметы при перемещении по полу — деформацию сдвига.

5. Предположим, что на полу стоит ящик (рис. 38). На него действует сила тяжести ​( vec{F}_т )​, направленная вертикально вниз. Ящик, взаимодействуя с полом, деформирует его и деформируется сам. И на ящик, и на пол действует сила упругости, характеризующая их взаимодействие. Сила упругости ​( vec{N} )​, действующая на ящик со стороны пола, приложена к ящику и направлена вертикально вверх; сила упругости ​( vec{P} )​, действующая со стороны ящика на пол, приложена к полу и направлена вертикально вниз. Эта сила называется весом тела.

Весом тела называют силу, с которой тело, вследствие его притяжения к Земле, действует на опору или подвес. В отличие от силы тяжести, вес тела приложен не к телу, а к опоре или к подвесу. Вес — это сила упругости.

6. Если тело покоится или движется равномерно и прямолинейно, вес тела численно равен силе тяжести, действующей на него: ​( vec{P}=mvec{g} )​.

На тело, движущееся вместе с платформой или подвесом вертикально вниз с ускорением ​( vec{a} )​, направленным в сторону движения, действуют сила тяжести ​( vec{F}_{т} )​ и сила упругости ​( N )​ со стороны опоры или подвеса (рис. 39, 40).

Второй закон Ньютона для этой ситуации: ​( mvec{g}+vec{N}=mvec{a} )​. В проекциях на координатную ось: ​( mg-N=ma )​ или ​( N=mg-ma )​. Поскольку ​( N=P )​, ​( P = m(g — a) )​.

Если тело движется вниз вместе с опорой или подвесом с ускорением, направленным так же, как и ускорение свободного падения, то его вес меньше силы тяжести, т.е. меньше веса покоящегося тела. Если ускорение тела равно ускорению свободного падения ​( vec{a}=vec{g} )​, то тело находится в состоянии невесомости.

В таком состоянии находится космонавт в космическом корабле, прыгун с трамплина во время полёта вниз.

7. На тело, движущееся вместе с платформой или подвесом вертикально вверх с ускорением ​( vec{a} )​, направленным в сторону движения, действуют сила тяжести ​( vec{F}_т )​ и сила упругости ​( vec{N} )​ со стороны опоры или подвеса (рис. 40).

Второй закон Ньютона для этой ситуации: ( mvec{g}+vec{N}=mvec{a} ). В проекциях на координатную ось: ​( mg-N=-ma )​ или ​( N=mg+ma )​. Поскольку ​( N=P )​, ​( P=m(g+a) )​.

Таким образом, если тело движется вверх вместе с опорой или подвесом с ускорением, направленным противоположно ускорению свободного падения, то его вес больше силы тяжести, т.е. больше веса покоящегося тела. Увеличение веса тела при движении с ускорением называют перегрузкой. Перегрузки испытывают космонавт в космическом корабле, пилот реактивного самолёта при взлёте и посадке.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Имеются две абсолютно упругие пружины. Под действием одной и той же силы первая пружина удлинилась на 8 см, а вторая — на 4 см. Сравните жёсткость ​( k_2 )​ второй пружины с жёсткостью ( k_1 ) первой пружины.

1) ​( k_1=k_2 )​
2) ( 4k_1=k_2 )
3) ( 2k_1=k_2 )
4) ( k_1=2k_2 )

2. Имеются две абсолютно упругие пружины: одна жёсткостью 200 Н/м, другая жёсткостью 400 Н/м. Сравните силу упругости ​( F_2 )​, возникающую во второй пружине, с силой упругости ( F_1 ), возникающей в первой пружине, при одинаковом их удлинении.

1) ​( F_2=F_1 )​
2) ​( F_2=4F_1 )
3) ​( 2F_2=F_1 )
4) ​( 0.5F_2=F_1 )

3. Ученик, растягивая пружину динамометра последовательно на 1Н, 2Н, ЗН и 4Н, каждый раз измерял её удлинение и результаты измерений вносил в таблицу. Определите по данным таблицы жёсткость пружины динамометра.

1) 0,02 Н/м
2) 0,5 Н/м
3) 2 Н/м
4) 50 Н/м

4. На рисунке приведены графики зависимости силы упругости от удлинения. Сравните жёсткость пружин.

1) ​( k_2=k_1 )​
2) ( k_2>k_1 )
3) ( k_2<k_1 )
4) ( k_2geq k_1 )

5. Учащийся выполнял эксперимент по измерению удлинения ​( x )​ пружин при подвешивании к ним грузов. Полученные учащимся результаты представлены на рисунке в виде диаграммы. Какой вывод о жёсткости пружин ​( k_1 )​ и ​( k_2 )​ можно сделать из анализа диаграммы, если к концам пружин были подвешены грузы одинаковой массы?

1) ​( k_2=4k_1 )​
2) ( k_1=2k_2 )
3) ( k_2=2k_1 )
4) ( k_1=k_2 )

6. Под действием силы 3 Н пружина удлинилась на 4 см. Чему равна сила, под действием которой удлинение этой пружины составит 6 см?

1) 3,5 Н
2) 4 Н
3) 4,5 Н
4) 5 Н

7. Две пружины растягиваются одинаковыми силами. Жёсткость первой пружины ​( k_1 )​ в 2 раза больше жесткости второй пружины ​( k_2 )​. Удлинение первой пружины ​( Delta l_1 )​, удлинение второй пружины ( Delta l_2 ) равно

1) ​( 0.5Delta l_1 )
2) ( 0.67Delta l_1 )
3) ( 1.5Delta l_1 )
4) ( 2.5Delta l_1 )

8. В лифте, движущемся вниз равноускоренно из состояния покоя, стоит ящик. Модуль веса ящика

1) равен модулю силы тяжести
2) больше модуля силы тяжести
3) меньше модуля силы тяжести
4) увеличивается с увеличением скорости лифта

9. Человек испытывает перегрузки при

1) равномерном движении вниз
2) равномерном движении вверх
3) равноускоренном движении вверх из состояния покоя
4) равноускоренном движении вниз с ускорением свободного падения

10. Различие веса тела на экваторе и на полюсе можно обнаружить

А. Взвешивая тело на рычажных весах
Б. Взвешивая тело на пружинных весах

Правильный ответ

1)только А
2)только Б
3) и А, и Б
4) ни А, ни Б

11. Установите соответствие между физической величиной (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Модуль силы упругости пружины
Б. Жёсткость пружины
B. Модуль удлинения пружины

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) уменьшается
2) увеличивается
3) не изменяется

12. Из приведённых ниже высказываний выберите два верных и запишите их номера в таблицу.

1) Закон Гука справедлив при любых деформациях.
2) Сила упругости направлена в сторону, противоположную деформации.
3) Жёсткость зависит только от материала, из которого изготовлено тело.
4) Вес тела всегда равен действующей на него силе тяжести.
5) Вес приложен к опоре или к подвесу.

Часть 2

13. Груз массой 5 кг начинают поднимать вертикально вверх с ускорением 2 м/с2. Чему равен вес груза?

Ответы