Как найти потенциальную энергию растяжения пружины

Во многих механизмах используется потенциальная и кинетическая энергия пружины. Их используют для выполнения различных действий. В отдельных узлах они фиксируют детали в определенном положении, не позволяя смещать в какую-либо сторону (барабан револьвера относительно корпуса). Другие пружинные системы возвращают исполнительный механизм в исходное положение (курок ручного огнестрельного оружия). Есть устройства, где узлы с гибкими свойствами совершают перемещения в устойчивое положение (механические стабилизаторы).
Работа связана с изменением геометрических параметров упругого тела. Прилагая нагрузку, заставляют эластичную деталь сжиматься (растягиваться или изгибаться). При этом наблюдается запасание энергии. Возвратное действие сопровождается набором скорости. Попутно возрастает кинетическая энергия.
Потенциальная энергия пружины
Рассматривая в качестве накопителя энергии пружину, следует отметить ее отличительные свойства от иных физических тел, которые могут накапливать энергетический потенциал. Традиционно понимается следующее: для накопления потенциала для последующего движения необходимо совершение движения в силовом поле:
Еп = F ⋅ l, Дж (Н·м),
где Еп– потенциальная энергия положения, Дж;
F – сила, действующая на тело, Н;
l – величина перемещения в силовом поле, м.
Энергия (работа) измеряются в Джоулях. Величина представляет произведение силы (Н) на величину перемещения (м).
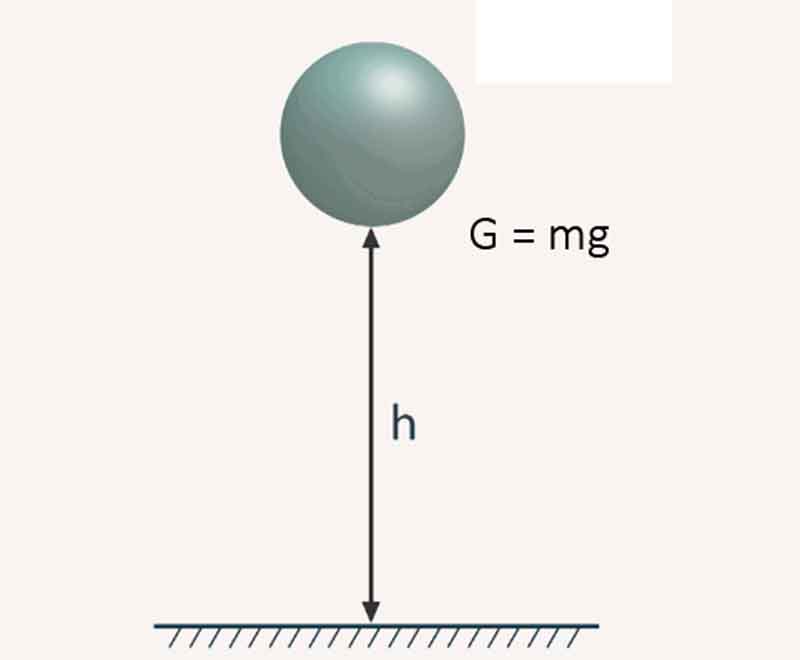
Если рассматривать условие в поле тяготения, то величина силы находится произведением ускорения свободного падения на массу. Здесь сила веса находится с учетом g:
Еп = G ⋅ h = m ⋅ g ⋅ h, Дж
здесь G – вес тела, Н;
m – масса тела, кг;
g – ускорение свободного падения. На Земле эта величина составляет g = 9,81 м/с².
Если расстраивается пружина, то силу F нужно определять, как величину, пропорциональную перемещению:
F = K ⋅ x, Н,
где k – модуль упругости, Н/м;
х – перемещение при сжатии, м.
Величина сжатия может изменяться по величине, поэтому математики предложили анализировать подобные явления с помощью бесконечно малых величин (dx) .
При наличии непостоянной силы, зависящей от перемещения, дифференциальное уравнение запишется в виде:
dEп = k ⋅ x ⋅ dx
здесь dEп – элементарная работа, Дж;
dx – элементарное приращение сжатия, Н.
Интегральное уравнение на конечном перемещении запишется в виде. Ниже вывод формулы:
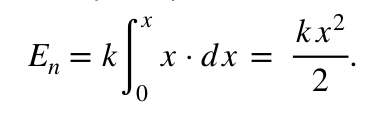
Пределами интегрирования является интервал от до х. Деформированная пружина приобретает запас по энергетическим показателям
Окончательно формула для расчета величины потенциальной энергии сжатия (растягивания или изгиба) пружины запишется формулой:
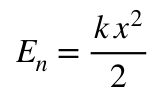
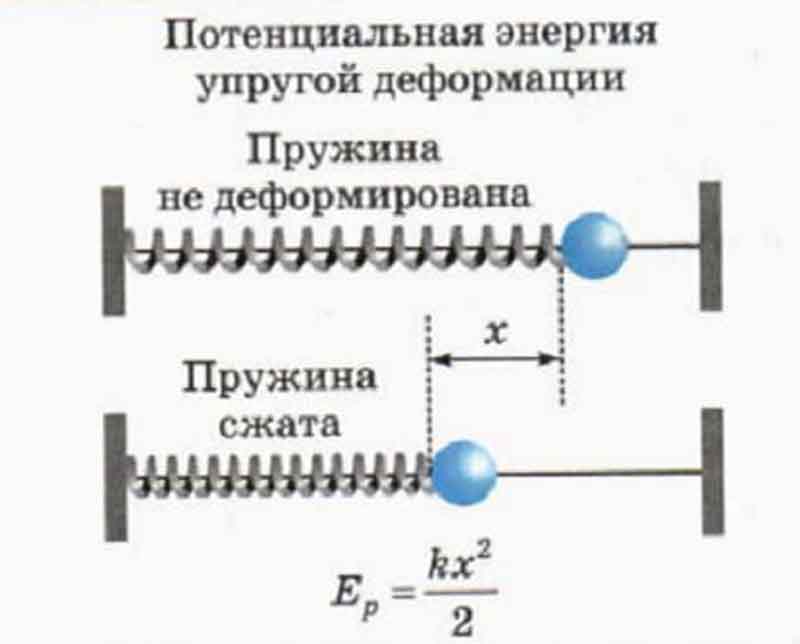
Закон сохранения механической энергии
Закон сохранения энергии существует независимо от желания наблюдателя. Все физические законы имеют статистический характер: существуют только подтверждения их выполнения, нет ни одного адекватно выполненного опыта, при котором наблюдается нарушение этой закономерности. Природные явления только подтверждают сохранность работы и энергозатрат, затраченных на ее выполнение.
На основании изложенного сформулировано положение:
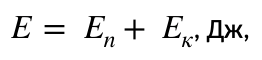
где Ек – кинетическая энергия, Дж.
Рассматривая перемещения тела, наблюдаются изменения потенциальной и кинетической энергий. При этом сумма значений остается постоянной.
Проще всего проследить за изменениями между разными видами энергетических показателей при рассмотрении движения маятника.
Из крайнего положения (шарик на нити отклонился в одну из сторон, Еп = max) тело движется под действием силы тяжести. При этом снижается запасенная энергия. Движение сопровождается увеличением скорости. Поэтому нарастают показатели динамического перемещения Ек.
В нижней точке не остается никаких запасенных эффектов от положения шарика. Он опустился да минимума. Теперь Ек =max.
Поучается, при совершении гармонических колебаний маятник поочередно накапливает то один, то другой вид энергии. Механические превращения из одного вида в другой налицо.
Кинетическая энергия
Движущееся тело характеризуется скалярной величиной (масса) и векторная величина (скорость). Если рассматривать реальное перемещение в пространстве, то можно записать уравнение для определения кинетической энергии:
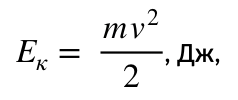
здесь v – скорость движения тела, м/с.

Использование кинетического преобразования можно наблюдать при колке орехов.
Приподняв камень повыше, далекие предки создавали необходимый потенциал для тяжелого тела.

Приподняв камень на максимальную высоту, разрешают ему свободно падать.
Двигаясь с высоты h, он набирает скорость
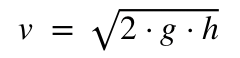
Поэтому в конце падения будет получена кинетическая энергия
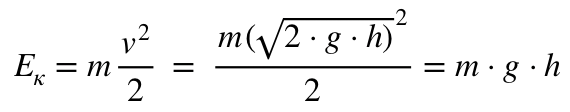
Рассматривая входящие величины, можно увидеть, как происходит преобразование величин. В конце получается расчетная формула для определения потенциальной энергии.
Даже на уровне вывода зависимостей можно наблюдать выполнение закона сохранения энергии твердого тела.
Использование энергии пружины на практике
Явление преобразования потенциальной энергии пружины в кинетическую используется при стрельбе из лука.
Натягивая тетиву, стреле сообщается потенциал для последующего движения. Чем жестче лук, а также ход при натягивании тетивы, тем выше будет запасенная энергия. Распрямляясь дуги этого оружия, придадут метательному снаряду значительную скорость.
В результате стрела полетит в цель. Ее поражающие свойства определятся величиной кинетической энергии (mv²/2).
Для гашения колебаний, возникающих при движении автомобиля, используют амортизаторы. Основным элементом, воспринимающим вертикальную нагрузку, являются пружины. Они сжимаются, а потом возвращают энергию кузову. В результате заметно снижается ударное воздействие. Дополнительно устанавливается гидроцилиндр, он снижает скорость обратного движения.

Рассмотренные явления используют при проектировании механизмов и устройств для автоматизации процессов в разных отраслях промышленности.
Видео: закон Гука и энергия упругой деформации.
Источник
Встречается довольно большое количество различных механизмов, частью которых является пружина. Этот конструктивный элемент характеризуется довольно большим количество различных особенностей, которые должны учитываться. Примером можно назвать понятие потенциальной энергии пружины. Рассмотрим все особенности данного вопроса подробнее.
Понятие потенциальной энергии пружины
При рассмотрении того, что такое потенциальная энергия пружины следует уделить внимание самому понятию – свойство, которым могут обладать тела при нахождении на земле. Этот момент определяет то, что ей могут обладать самые разнообразные изделия, в том числе рассматриваемое. К особенностям рассматриваемого понятия можно отнести следующее:
- Потенциальная энергия в рассматриваемом случае формируется по причине изменения состояния. Даже при несущественном смещении витков относительно друг друга считается изменением состояния подобного изделия.
- Для того чтобы изменить состояние изделия совершается определенное действие. Зачастую для этого проводится прикладывание усилия. При этом важно провести расчет требуемого усилия для сжатия витков.
- После выполнения определенной работы большая часть усилия, которое было потрачено на выполнение действия высвобождается при определенных обстоятельствах. Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.
Она также широко применяется при создании самых различных механизмов, к примеру, заводных часов. При проектировании различных механизмов учитывается закон сохранения механической силы, которая характеризуется довольно большим количеством особенностей.
Закон сохранения механической энергии
Согласно установленным законам механическое воздействие консервативной механической системы сохраняется во времени. Этот момент определяет то, что потенциальная энергия деформированной пружины не может возникнуть сама или исчезнуть куда-нибудь. Именно поэтому для ее создания нужно приложить соответствующее усилие.
Рассматриваемый закон относится к категории интегральных равенств. Эта закономерность определяет то, что он складывается их действия дифференциальных законов, является свойством или признаком совокупного воздействия.
Для проведения соответствующих расчетов должна применяться определенная формула. Сила, с которой оказывается воздействие, не является постоянной. Именно поэтому для ее вычисления применяется графический метод. Самая простая зависимость может быть описана следующим образом: F=kx. При применении подобной зависимости построенная координатная линия будет представлена прямой линией, которая расположена под углом относительно системы координат.
Приписать подобному устройству потенциальную энергию можно только в том случае, если она равна максимальной работе и не зависит от условной траектории движения. Проведенные исследования указывают на то, что подобная работа подчиняется закону Гука. Для определения основного показателя применяется следующая формула: U=kk2/2.
Для деформирования витков к ним должно быть приложено определенное усилие, так как в противном случае кинетическая сила не возникнет.
Динамика твердого тела
Некоторые определить выражения (определяется при применении наиболее подходящих формул) можно только с учетом правил, касающихся динамики твердых объектов. Этому вопросу посвящен целый раздел. При расчете потенциальной энергии сжатой пружины также применяются некоторые законы этого раздела
Динамика твердого тела рассматривается по причине того, что в большинстве случаев механизм совершает действие, связанное с непосредственным перемещением какого-либо объекта.
Рассматриваемое свойство изделия может изменяться в зависимости от динамики твердого тела. Это связано с тем, что на изделие оказывается и воздействие со стороны окружающей среды. Примером можно назвать трение или нагрев.
Момент силы и момент импульса относительно оси
Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.
Момент импульса – величина, которая применяется для определения количества вращательного движения.
Среди особенностей подобного показателя можно отметить следующее:
- Масса вращения. Объект может характеризоваться различной массой.
- Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
- Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.
Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.
Уравнение движения вращающегося тела
Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек. При этом отметим нижеприведенные особенности:
- Прямая, которая соединяет две точки, выступает в качестве оси вращения.
- Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
- Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.
Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt. В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной.
Источник
Все формулы по физике и математике
Темы по физике
- Механика (56)
- Кинематика (19)
- Динамика и статика (32)
- Гидростатика (5)
Темы по математике
- Квадратный корень, рациональные переходы (1)
- Квадратный трехчлен (1)
- Координатный метод в стереометрии (1)
- Логарифмы (1)
- Логарифмы, рациональные переходы (1)
- Модуль (1)
- Модуль, рациональные переходы (1)
- Планиметрия (1)
- Прогрессии (1)
- Производная функции (1)
- Степени и корни (1)
- Стереометрия (1)
- Тригонометрия (1)
- Формулы сокращенного умножения (1)
Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.
Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем упругую энергию растянутой пружины.
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.
Потенциальная энергия :
Кинетическая энергия
Тут мы использовали :
— Потенциальная энергия упруго деформированного тела
— Коэффициент упругости пружины
— Деформация пружины
Груз массой m, подвешенный к пружине, совершает колебания с периодом T и амплитудой Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу груза?
Для каждой величины определите соответствующий характер изменения:
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период колебаний | Максимальная потенциальная |
энергия пружины
Период колебаний связан с массой груза и жесткостью пружины k соотношением При уменьшении массы период колебаний уменьшится. Частота обратно пропорциональна периоду, значит, частота увеличится.
С максимальной потенциальной энергией пружины все немного сложнее. Для ответа на вопрос, что с ней произойдет существенно, что пружина ориентирована вертикально (для горизонтального пружинного маятника при неизменной амплитуде данная величина, естественно, останется неизменной). Действительно, когда к вертикальной пружине подвешивают груз, она сразу немного растягивается, чтобы уравновесить силу тяжести, действующую на груз. Определим это начальное растяжение: Именно это состояние является положением равновесия для вертикального пружинного маятника, колебания происходят вокруг него, груз поднимается и опускается из этого положения на величину амплитуды. При движении вниз из положения равновесия пружина продолжает растягиваться, а значит, потенциальная энергия пружины продолжает увеличиваться. При движении вверх из положения равновесия, сперва деформация пружины уменьшается, а если то пружины начнет сжиматься. Максимальной потенциальной энергии пружины соответствует состояние, когда она максимально растянута, а значит, в нашем случае, это положение, когда груз опустился максимально вниз. Таким образом, максимальная потенциальная энергия пружины равна
Из этой формулы видно, что для вертикального пружинного маятника при неизменной амплитуде и уменьшении массы груза максимальная потенциальная энергия пружины уменьшится.
Встречается довольно большое количество различных механизмов, частью которых является пружина. Этот конструктивный элемент характеризуется довольно большим количество различных особенностей, которые должны учитываться. Примером можно назвать понятие потенциальной энергии пружины. Рассмотрим все особенности данного вопроса подробнее.
Понятие потенциальной энергии пружины
При рассмотрении того, что такое потенциальная энергия пружины следует уделить внимание самому понятию – свойство, которым могут обладать тела при нахождении на земле. Этот момент определяет то, что ей могут обладать самые разнообразные изделия, в том числе рассматриваемое. К особенностям рассматриваемого понятия можно отнести следующее:
- Потенциальная энергия в рассматриваемом случае формируется по причине изменения состояния. Даже при несущественном смещении витков относительно друг друга считается изменением состояния подобного изделия.
- Для того чтобы изменить состояние изделия совершается определенное действие. Зачастую для этого проводится прикладывание усилия. При этом важно провести расчет требуемого усилия для сжатия витков.
- После выполнения определенной работы большая часть усилия, которое было потрачено на выполнение действия высвобождается при определенных обстоятельствах. Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.
Она также широко применяется при создании самых различных механизмов, к примеру, заводных часов. При проектировании различных механизмов учитывается закон сохранения механической силы, которая характеризуется довольно большим количеством особенностей.
Закон сохранения механической энергии
Согласно установленным законам механическое воздействие консервативной механической системы сохраняется во времени. Этот момент определяет то, что потенциальная энергия деформированной пружины не может возникнуть сама или исчезнуть куда-нибудь. Именно поэтому для ее создания нужно приложить соответствующее усилие.
Рассматриваемый закон относится к категории интегральных равенств. Эта закономерность определяет то, что он складывается их действия дифференциальных законов, является свойством или признаком совокупного воздействия.
Для проведения соответствующих расчетов должна применяться определенная формула. Сила, с которой оказывается воздействие, не является постоянной. Именно поэтому для ее вычисления применяется графический метод. Самая простая зависимость может быть описана следующим образом: F=kx. При применении подобной зависимости построенная координатная линия будет представлена прямой линией, которая расположена под углом относительно системы координат.
Приписать подобному устройству потенциальную энергию можно только в том случае, если она равна максимальной работе и не зависит от условной траектории движения. Проведенные исследования указывают на то, что подобная работа подчиняется закону Гука. Для определения основного показателя применяется следующая формула: U=kk2/2.
Для деформирования витков к ним должно быть приложено определенное усилие, так как в противном случае кинетическая сила не возникнет.
Динамика твердого тела
Некоторые определить выражения (определяется при применении наиболее подходящих формул) можно только с учетом правил, касающихся динамики твердых объектов. Этому вопросу посвящен целый раздел. При расчете потенциальной энергии сжатой пружины также применяются некоторые законы этого раздела
Динамика твердого тела рассматривается по причине того, что в большинстве случаев механизм совершает действие, связанное с непосредственным перемещением какого-либо объекта.
Рассматриваемое свойство изделия может изменяться в зависимости от динамики твердого тела. Это связано с тем, что на изделие оказывается и воздействие со стороны окружающей среды. Примером можно назвать трение или нагрев.
Момент силы и момент импульса относительно оси
Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.
Момент импульса – величина, которая применяется для определения количества вращательного движения.
Среди особенностей подобного показателя можно отметить следующее:
- Масса вращения. Объект может характеризоваться различной массой.
- Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
- Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.
Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.
Уравнение движения вращающегося тела
Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек. При этом отметим нижеприведенные особенности:
- Прямая, которая соединяет две точки, выступает в качестве оси вращения.
- Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
- Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.
Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt. В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Источник
