Энергия упругой деформации пружины при ее растяжении на 5 см равна
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
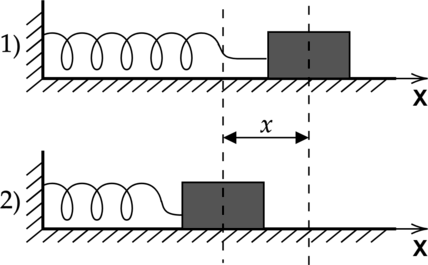
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
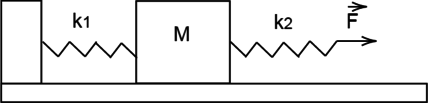
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]
Ответ: 400
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)

Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
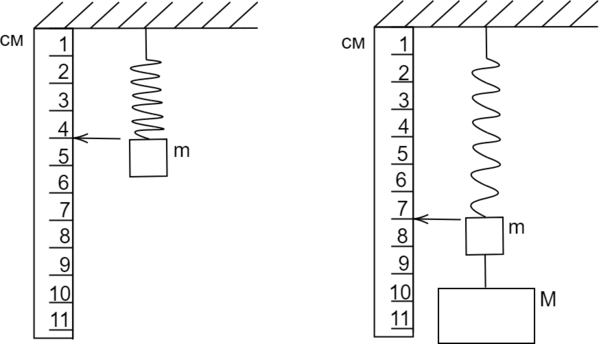
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
