Экспериментальные исследования при растяжении
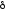
Диаграмма растяжения
Испытание на растяжение выполняют на машинах, развивающих усилие от нескольких килограммов до 2000 тс и более. Стальные образцы на растяжение (рис. 5.1) обычно изготавливают круглого сечения диаметром d, цилиндрическая рабочая часть образца имеет длину не менее /о = 10d.

Рис. 5.1
На рабочей части образца наносятся риски на расстоянии, равном d. Он имеет конические вставки для плавного перехода от рабочей части к головкам, которые предназначены для закрепления образца в захватных приспособлениях машины. Крайние риски на рабочей части образца удалены от конических вставок, это позволяет (как и сами конические вставки) уменьшить влияние концентрации напряжений в месте резкого изменения диаметра на расчётную часть образца.
Зависимость между приложенной нагрузкой F и абсолютной продольной линейной деформацией образца назовём диаграммой растяжения (рис. 5.2). Диаграмма состоит из четырёх зон. Зона ОА — зона упругости, в пределах которой деформации образца упругие, график F — А/ — прямая линия. Зона АВ — площадка текучести, зона общей текучести, в пределах этой зоны интенсивно развиваются пластические деформации при почти постоянной нагрузке. У ряда материалов — легированной стали, бронзы, алюминиевых сплавов — площадки текучести нет (рис. 5.3). Зона ВС — зона упрочнения, в пределах этой зоны увеличивается нагрузка при возрастающей деформации как пластической, так и упругой. В образце намечается место будущего разрыва — зарождается шейка (местное утоныпение образца), рис. 5.4, а.

Рис. 5.2

Рис. 5.3
В зонах общей текучести и упрочнения на поверхности образца из малоуглеродистой стали появляются полосы скольжения — линии Людерса (1859 г.) — Д.К. Чернова (1884 г.); причина их появления — максимальные касательные напряжения, действующие под углом 45° к оси образца (рис. 5.4, б). Зона CD — зона местной текучести, в пределах этой зоны пластические деформации интенсивно развиваются в шейке. Сила, выдерживаемая образцом, уменьшается. Образец разрывается в шейке (рис. 5.4, а).

Рис. 5.4
Если образец в зоне упрочнения разгрузить, то разгрузка произойдет по прямой КМ, параллельной О А. При повторном нагружении на графике F — А/ получим кривую МК (рис. 5.5, а). Область, заключенная между прямой КМ и кривой МК, — петля гистерезиса, которая является свидетельством необратимых потерь энергии на нагрев, на преодоление сил внутреннего трения (рассеивание энергии). Поскольку площадь петли гистерезиса невелика, пренебрегаем ею. Тогда линия повторного нагружения пройдёт по прямой МК (рис. 5.5, б).
На рис. 5.5 стрелками показаны нагружение, разгрузка и последующее нагружение образца. Из рис. 5.5, б следует, что поскольку прямая МК параллельна линии О А, вплоть до точки К образец сохраняет упругие свойства.

Рис. 5.5
На рис. 5.5 обозначены: Д/ост — остаточная абсолютная линейная деформация; А1У — упругая абсолютная линейная деформация, соответствующая точке К диаграммы. Явление повышения упругих свойств материала за счёт предварительного его остаточного (пластического) деформирования назовём наклёпом. Наклёпу подвергают листовую медь прокаткой в холодном состоянии на валках, тросы и цепи — вытяжкой силами выше эксплуатационных. При штамповке тонкостенных конструкций наклёп нежелателен, и его снимают отжигом.
Источник
Напряженное состояние в точке характеризуется совокупностью нормальных  и касательных
и касательных  напряжений, возникающих на произвольно расположенных площадях, проходящих через эту точку.
напряжений, возникающих на произвольно расположенных площадях, проходящих через эту точку.
Пусть брус нагружен осевой силой F (рис. 2.8, а). Определим усилие и напряжение в наклонном сечении.
Рассечем брус наклонной плоскостью под углом  к нормальному сечению (
к нормальному сечению ( – площадь поперечного сечения,
– площадь поперечного сечения,  – площадь сечения, наклоненного под углом
– площадь сечения, наклоненного под углом ) и рассмотрим равновесие отсеченной части (рис. 2.8, б):
) и рассмотрим равновесие отсеченной части (рис. 2.8, б):


Рис. 2.8
где R – равнодействующая внутренних сил в наклонной плоскости.
Разложив R по двум направлениям, получим  где
где 
Так как  , то нормальное
, то нормальное  и касательное
и касательное  напряжения в наклонном сечении определяются соответственно но формулам
напряжения в наклонном сечении определяются соответственно но формулам
 (2.20)
(2.20)
где  – нормальные напряжения в нормальном сечении.
– нормальные напряжения в нормальном сечении.
Проанализируем выражения (2.20).
Сформулируем закон суммы нормальных напряжений:

Тогда
 (2.21)
(2.21)
Сумма нормальных напряжений, действующих на двух взаимно перпендикулярных площадках, есть величина постоянная, равная нормальному напряжению.
Аналогично устанавливается закон парности касательных напряжений:
 (2.22)
(2.22)
Касательные напряжения, действующие на двух взаимно перпендикулярных площадках, равны по абсолютной величине и противоположно направлены.
Испытание материалов на растяжение (сжатие) осуществляется с целью определения механических характеристик следующих свойств материала: упругости, пластичности, прочности и твердости. Характеристиками упругости являются предел упругости и модуль упругости; характеристиками пластичности – предел текучести и относительное остаточное удлинение; характеристикой прочности является предел прочности. Механические свойства материалов определяются в лабораториях механических испытаний на разрывных машинах по образцам, изготовленным из исследуемого материала. Графическое представление зависимости между действующей силой F и удлинением  называется диаграммой растяжения или сжатия образца
называется диаграммой растяжения или сжатия образца  . Поскольку исследуется не конкретный образец, а материал, то принято по результатам испытаний ряда образцов строить диаграмму материала в относительных величинах. С этой целью усилия F относят к первоначальной площади
. Поскольку исследуется не конкретный образец, а материал, то принято по результатам испытаний ряда образцов строить диаграмму материала в относительных величинах. С этой целью усилия F относят к первоначальной площади  , а абсолютное удлинение
, а абсолютное удлинение  – к первоначальной длине образца
– к первоначальной длине образца  . Получается диаграмма материала
. Получается диаграмма материала  .
.
Пластичные материалы разрушаются при больших остаточных деформациях. К таким материалам можно отнести, например, мягкую углеродистую сталь, медь, алюминий. Хрупкие материалы разрушаются при малых остаточных деформациях. К хрупким материалам можно отнести закаленную сталь, чугун, стекло, бетон, камень и др. Хрупкие материалы разрушаются главным образом в результате нарушения сопротивления отрыву частиц, пластичные материалы – вследствие нарушения сопротивления сдвигу. В ряде случаев хрупкие материалы могут находиться в пластичном состоянии, и наоборот.

Рис. 2.9
Диаграмма растяжения малоуглеродистой стали (пластичного материала) показана на рис. 2.9. Рассмотрим характерные точки и участки диаграммы.
Точка 1 – конец прямолинейного участка, участок 0–1 называется участком прямолинейной зависимости между нормальным напряжением и относительным удлинением, что отражает закон Гука  Точка 1 соответствует пределу пропорциональности:
Точка 1 соответствует пределу пропорциональности:  , где
, где  – нагрузка, соответствующая проделу пропорциональности. Несколько выше точки 1 находится точка
– нагрузка, соответствующая проделу пропорциональности. Несколько выше точки 1 находится точка , соответствующая пределу упругости ау, т.е. наибольшему напряжению, при котором в материале еще нет остаточных деформаций:
, соответствующая пределу упругости ау, т.е. наибольшему напряжению, при котором в материале еще нет остаточных деформаций: , где
, где – нагрузка, соответствующая пределу упругости.
– нагрузка, соответствующая пределу упругости.
Относительная деформация, соответствующая пределу упругости (весьма близкая к пределу пропорциональности), для малоуглеродистой стали примерно достигает 0,1%.
За точкой  возникают заметные остаточные деформации. В точке 2 диаграммы материал переходит в область пластичности – наступает явление текучести материала. Участок 2–3 параллелен оси абсцисс (площадка текучести). Для данной площадки характерен рост деформации при постоянном напряжении. Напряжение, соответствующее участку 2–3, называется пределом текучести:
возникают заметные остаточные деформации. В точке 2 диаграммы материал переходит в область пластичности – наступает явление текучести материала. Участок 2–3 параллелен оси абсцисс (площадка текучести). Для данной площадки характерен рост деформации при постоянном напряжении. Напряжение, соответствующее участку 2–3, называется пределом текучести:

где  – усилие, соответствующее пределу текучести.
– усилие, соответствующее пределу текучести.
От точки 3 до точки 4 наблюдается упрочение материала. В районе точки 4 происходит местное сужение образца – появляется так называемая шейка. Отношение 
 называется пределом прочности.
называется пределом прочности.
Участку 4–5 соответствует быстрое уменьшение сечения образца в зоне шейки. В точке 5происходит разрыв образца при разрушающей нагрузке 
Если разрушившийся образец сложить и определить его длину после разрушения, то можно определить остаточное удлинение образца (остаточную деформацию)


где  – длина рабочей части образца после разрушения;
– длина рабочей части образца после разрушения;  исходная длина рабочей части образца.
исходная длина рабочей части образца.
Условно материал считается пластичным, если  , и хрупким, если
, и хрупким, если 
При механических испытаниях материала также определяется модуль упругости по участку прямой пропорциональной зависимости диаграммы. Таким образом, в результате механических испытаний материалов получают механические характеристики 
Большинство материалов не имеет явно выраженной площадки текучести, поэтому определяют технический предел текучести по величине остаточной деформации. Техническим пределом текучести принято считать такое напряжение, при котором остаточная деформация  , или когда
, или когда  . Предел текучести при растяжении обозначается
. Предел текучести при растяжении обозначается  , а предел текучести при сжатии –
, а предел текучести при сжатии – 
Источник
Для определения свойств материала при
его растяжении и сжатии (до стадии
разрушения) производят механические
испытания образцов в лаборатории.
Материалы по их механическим качествам
можно разделить на две группы:
пластичные и хрупкие. Первые разрушаются
только после значительной
остаточной деформации, хрупкие же — при
весьма малых остаточных
деформациях. К пластичным материалам
относятся: малоуглеродистая
сталь, медь, бронза и др.; к хрупким —
чугун, бетон, камень, кирпич и др.
Один и тот же материал в зависимости от
условий, в которых он находится,
может вести себя и как пластичный и как
хрупкий. Например, «мягкая сталь»
в некоторых случаях сложного
сопротивления, в особенности
при наличии надрезов, иногда ведет себя
как хрупкий материал. Та же
сталь обладает хорошими пластическими
свойствами при нормальной
положительной температуре, а при низкой
(отрицательной)
температуре она приобретает свойства
хрупкости. Таким образом, было бы
правильнее говорить о хрупком и
пластическом состояниях
материалов.
3.6. Испытания материала на растяжение
Образец стандартной формы закрепляют
концами в захваты разрывной
машины. Затем образец растягивают
постепенно возрастающей
нагрузкой без толчков и ударов. В
процессе испытания последовательно
отмечают величины нагрузок и
измеряют соответствующие
им удлинения. Испытательные машины
обычно снабжены специальным
автоматическим приспособлением,
вычерчивающим так называемую
диаграмму растяжения, на которой
по оси ординат величины нагрузок, а
по оси абсцисс — величины абсолютных
удлинений.
Для удобства сравнения результатов
испытания нескольких образцов,
имеющих разные размеры, диаграмму
растяжения обычно перестраивают
в координаты
 и
и (рис. 3.5).
(рис. 3.5).
В начальный момент, соответствующий
началу координат диаграммы,
 =0
=0
и =0.
=0.
При постепенном увеличении нагрузки
стержень получает удлинение,
которое растет прямо пропорционально
силе до точкиAдиаграммы.
ПрямаяOAграфически выражает
закон Гука.
Напряжение, соответствующее крайней
точке AпрямойOA, называется
пределом пропорциональности и обозначается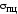 .
.
Для стали марки Ст. 3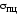 =200
=200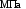 .
.
AB— кривая выпуклостью вверх. Прямая
пропорциональность между и
и нарушена и деформации растут быстрее
нарушена и деформации растут быстрее
напряжений.
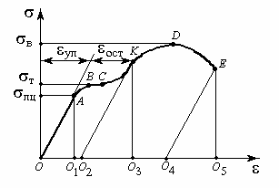
Рис. 3.5
Участок BC— горизонтальная линия —
деформации растут даже без увеличения
нагрузки, и материал, как говорят,
«течет».BC— площадка
текучести материала. Напряжение,
соответствующее точкеB— предел
текучести материала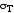 .
.
Для стали марки Ст. 3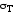 =240
=240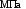 .
.
В процессе течения материала на образце
появляются едва заметные
наклонные штрихи под углом около
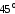 к его поперечному сечению
к его поперечному сечению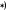 (штрихи Людерса — Чернова).
(штрихи Людерса — Чернова).
Появление этих линий можно объяснить
пластическими деформациями, вызванными
главным образом касательными
напряжениями.
От точки CдоD— пологая кривая.
Помимо упругого удлинения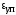 образец получает еще значительное
образец получает еще значительное
остаточное удлинение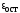 .
.
ТочкаD
соответствует
наибольшему значению нагрузки на
образец. Напряжение, соответствующее
этой точке, называется пределом
прочности
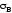 материала, т. е. наибольшим из
материала, т. е. наибольшим из
возможных для материала напряжением,
отнесенным к первоначальной
площади поперечного сечения образца.
Для стали марки Ст. 3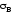 =420
=420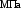 .
.
По достижении наибольшей нагрузки
деформация, приводящая к разрушению,
сосредотачивается в одном месте образца,
в результате чего появляется
сужение его поперечного сечения (шейка),
которая становится
___________________________
 Строго говоря, как
Строго говоря, как
показали теоретические (работа А. Надаи)
и экспериментальные
(работа А.Р. Ржаницына) исследования,
штрихи Людерса-Чернова направлены
под углом
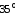 к поперечному сечению образца.
к поперечному сечению образца.
все
тоньше и тоньше, и, наконец, при напряжении,
соответствующем точке E,
происходит разрыв.
Деформация, выраженная абсциссой
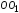 ,
,
т. е. соответствующая напряжению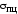 является упругой деформацией. Она
является упругой деформацией. Она
исчезает после удаления нагрузки.
Если снять нагрузку с образца за
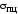 (например, в точкеK), то линия
(например, в точкеK), то линия
разгрузки изобразится прямой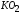 ,
,
параллельной прямойOA. В данном
случае образец получит кроме упругого
удлинения (отрезок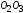 )
)
и остаточное удлинение (отрезок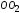 ).
).
Абсцисса
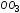 представляет собой полное удлинение
представляет собой полное удлинение
при напряжении, соответствующем
точкеKдиаграммы.
Таким образом, за пределом пропорциональности
материала относительная деформация
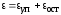 .
.
Линия
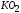 диаграммы параллельна линииOA,
диаграммы параллельна линииOA,
выражающей закон Гука. Следовательно,
и за пределом пропорциональности упругие
деформации пропорциональны
напряжениям.
Для оценки степени пластичности материала
служат величины (в процентах):
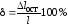 — относительное остаточное удлинение
— относительное остаточное удлинение
при разрыве (абсцисса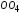 );
);
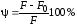 — относительное остаточное сужение, где
— относительное остаточное сужение, где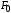 — площадь поперечного сечения в месте
— площадь поперечного сечения в месте
разрыва (в шейке); — первоначальная площадь
— первоначальная площадь
поперечного сечения.
Чем больше
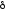 и
и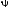 ,
,
тем более пластичный материал. Для
обычных сталей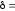 8-28
8-28
%,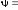 30-70
30-70
%.
Немного выше, но очень близко к точке Aна диаграмме лежит точка, характеризующая
собой предел упругости материала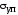 .
.
Это напряжение вызывает очень
малые остаточные деформации (порядка
0,001 — 0,005 %), которыми можно пренебречь.
Поэтому практически считают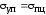 .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
В зависимости от условий эксплуатации деталей в расчетах используют различные характеристики механических свойств материалов, определяемые экспериментально при статических, динамических, повторно-переменных нагрузках, нормальной, повышенной или низкой температуре, различных видах деформации (растяжение, сжатие, кручение, изгиб).
Результаты испытания зависят ог формы и размеров образцов, скорости нагружения, температуры, поэтому условия проведения испытания стандартизованы (ГОСТ 1497—84).
Во время статических испытаний образцы нагружаются нагрузками, медленно возрастающими от нулевого значения до конечного, что позволяет пренебрегать силами инерции.
При динамических испытаниях (испытания на удар) нагрузка передается на испытуемый объект сразу всей величиной или даже с некоторой начальной скоростью.
Наиболее распространенным является статическое испытание материалов на растяжение.
Это объясняется тем, что, во-первых, при сравнительно простом оборудовании в исследуемой зоне образца можно создать однородность напряженного состояния для всех его точек и, во-вторых, по механическим характеристикам материала, полученным при статическом испытании на растяжение, часто можно судить и о поведении материала при других видах деформации.
Испытания проводят на стандартных образцах (рис. 2.20) или на образцах, геометрически подобных стандартным. Обычно принимают 1=11,3, где /0 — начальная длина испытуемой части образца; А0 — начальная площадь поперечного сечения образца, что соответствует /0 = 10 с1.

Рис. 2.20. Стандартные образцы:
а — образец с круглым сечением; б — образец с прямоугольным сечением
Испытания проводят на разрывных и универсальных машинах с механическим или гидравлическим приводом. При испытании образцы нагружают нагрузкой, постепенно возрастающей от нуля до значения, при котором происходит разрушение образца. При этом производится, как правило, автоматическая запись диаграммы, которая показывает зависимость между растягивающей силой Г и соответствующим ей удлинением А/ исследуемой зоны образца.
Каждый материал в зависимости от его состава и технологии производства дает характерную для него диаграмму.
Естественно, если подвергнуть испытанию образцы из одного материала, но разных размеров, то и диаграммы получаются разные. Диаграмма в координатах Р— А/характеризует не только собственно материал, но и образец, так как зависит от его размеров.
Чтобы охарактеризовать непосредственно материал, исключить влияние начальных размеров образца и получить механические характеристики материала, эту диаграмму перестраивают в координатах а — ?, т.е. все значения нагрузок делят на начальную площадь поперечного сечения образца, а соответствующие им удлинения А1 — на начальную длину /0.
Диаграмма, перестроенная в новых координатах о — ?, естественно, подобна диаграмме Р— А/.
На рис. 2.21 изображена условная диаграмма растяжения, характерная для малоуглеродистой стали. Эта диаграмма называется условной потому, что при ее построении не учитывается изменение площади поперечного сечения образца.

е
Рис. 2.21. Диаграмма растяжения
На диаграмме отмечены точки, которым соответствуют напряжения, являющиеся механическими характеристиками материала.
На участке АО диаграмма изображается наклонной прямой, так как между напряжением о и продольной деформацией ? существует пропорциональная зависимость.
Напряжение, соответствующее точке А диаграммы, называется пределом пропорциональности — апц.
Предел пропорциональности — это наибольшее напряжение, до которого справедлив закон Гука.
Если образец нагрузить до напряжений, не превышающих предела пропорциональности, а затем разгрузить до нуля, то линия разгрузки совпадает с линией нагрузки АО, т.е. при снятии нагрузки исчезнет и деформация. Это означает, что на участке АО материал работает в области упругих деформаций. Зона АО носит название зоны упругости. Выше точки А диаграмма искривляется и закон Гука нарушается. Максимальное напряжение, при котором в материале не появляются остаточные деформации, называется пределом упругости — у На диаграмме это точка В, которая лежит несколько выше точки А.
Нахождение точных значений супц и оу сопряжено с большими трудностями.
Практически за предел упругости принимают то напряжение, при котором остаточная деформация равна наперед заданной величине, например 0,001%, или 0,003%, или 0,005%, и соответственно пределы упругости обозначают а0 001, о0 003, а0 005.
Диаграмма малоуглеродистой стали имеет так называемую площадку текучести — участок, на котором наблюдается заметный рост деформации без заметного роста напряжений. Напряжение, соответствующее точке С диаграммы, называется пределом текучести — ат.
Предел текучести — это напряжение, при котором происходит заметный рост деформации без увеличения нагрузки. При достижении предела текучести материал начинает «течь».
Начало пластических деформаций можно заметить как по диаграмме — появляется горизонтальный участок, так и по самому образцу. Если поверхность образца полированная, то она начинает тускнеть и на ней можно заметить сетку линий, наклоненных к оси образца примерно под углом 45“ (рис. 2.22). Эти линии, называемые линиями Чернова — Людерса, свидетельствуют о происходящих сдвигах кристаллов.

Рис. 2.22. Линии Чернова — Людерса
После окончания стадии текучести материал снова начинает сопротивляться деформации. Если образец нагрузить до напряжений выше предела пропорциональности, например до точки К, а затем разгрузить, то разгрузка пойдет по прямой КЬ, параллельной АО (см. рис. 2.21). При нагружении образца до напряжения, соответствующего напряжению точки К диаграммы, в нем возникнет суммарная деформация ?, равная сумме упругой еу (исчезающей при снятии нагрузки) и остаточной еосг
Напряжение, соответствующее верхней точке диаграммы — А называют временным сопротивлением или пределом прочности — аи, или, другими словами, пределом прочности материала называется а|1Ч условное напряжение, равное отношению максимальной нагрузки, которую может выдержать образец, к начальной площади поперечного сечения образца.
Пределы текучести и прочности материала являются его основными механическими характеристиками.
После достижения предела прочности в одном месте образца появляется еле заметное на глаз сужение (шейка), которое становится все более и более заметным. Площадь сечения шейки быстро уменьшается, и вскоре на этом месте происходит разрушение (рис. 2.23). С появлением шейки нагрузка начинает падать, поэтому и условные напряжения на участке ОЕ падают, так как диаграмму строят без учета изменения площади сечения образца. Напряжение в точке Е диаграммы называют напряжением разрушения материала. Но это напряжение чисто условное. Истинное напряжение в момент разрушения значительно превосходит не только условное напряжение, но и предел прочности и равно отношению разрушающей нагрузки к площади сечения шейки.

Рис. 2.23. Образование шейки
на образце
Так, для стали марки СтЗ предел текучести равен примерно 240 МПа, предел прочности — приблизительно 380 МПа, а истинное напряжение в момент разрыва образца достигает приблизительного значения 800-1000 МПа.
При механических испытаниях материалов получают также характеристики, по которым оценивается пластичность материалов — относительное остаточное удлинение при разрыве (8) и относительное остаточное уменьшение площади сечения образца при разрыве (V):
^ о)Ао 5 ? — {Л) ~ А к )/Л) »
где /0, 1К — длина исследуемой зоны образца соответственно до нагружения и после разрыва; А{) и Ак — площади поперечного сечения образца соответственно до нагружения и после разрыва в самом узком месте шейки.
Часто 8 и ц/ выражают в процентах:
«=(/*-/о)//»• 100% ; V = (л — *к)/А’ 100%.
Для стали марки СтЗ 6« 20…25%, а у = 60…70% .
Отметим, что ярко выраженную площадку текучести имеют только диаграммы растяжения низкоуглеродистой стали и некоторых сплавов цветных металлов. На рис. 2.24 показан для сравнения вид диаграммы растяжения сталей с различным содержанием углерода; из рисунка видно, что с повышением процента содержания углерода увеличивается прочность стали и уменьшается ее пластичность.

Рис. 2.24. Диаграммы растяжения сталей с различным содержанием
углерода
Для пластичных материалов, диаграммы растяжения которых не имеют ярко выраженной площадки текучести (средне- и высокоуглеродистые, легированные стали) или совсем ее не имеют (медь, дюралюминий) (рис. 2.25), вводится понятие условного предела текучести, т.е. напряжения, при котором остаточная деформация равна 80СТ= 0,002 или, что-то же самое, еост = 0,2%. Условный предел текучести в этом случае обозначают а0 2. В некоторых случаях принимают предел еост = 0,5% и соответственно этому условный предел текучести обозначают о0 5.

Рис. 2.25. Диаграмма растяжения
высокопластичных материалов
Обычно в таблицах механических характеристик материалов условный и физический пределы текучести не разграничивают и вводят единое обозначение ат.
Таким образом, подводя итоги, можно сделать вывод: характеристикой упругих свойств материалов являются пределы пропорциональности и упругости, характеристикой прочности — предел текучести и предел прочности, характеристикой пластических свойств материалов — относительное остаточное удлинение и относительное остаточное сужение образца при разрыве.
Ряд материалов, например чугун, стекло, каменные материалы, кирпич, бетон, относятся к так называемым хрупким материалам. Диаграмма растяжения таких материалов существенно отличается от диаграмм пластичных материалов. На рис. 2.26 показан примерный вид диаграммы растяжения чугуна. К характерной особенности всех хрупких материалов можно отнести разрушение образцов при ничтожно малых остаточных деформациях. На диаграмме растяжения почти не получается прямолинейного участка, искривление начинается при сравнительно небольших напряжениях, но сами деформации незначительны, так что отклонение от закона Гука невелико, поэтому в практических расчетах это отклонение не учитывается. При приближении к пределу прочности кривая быстро отклоняется вправо и происходит хрупкое разрушение образца.

Рис. 2.26. Примерная диаграмма растяжения
образца из чугуна
По полученным диаграммам растяжения можно производить оценку прочности и пластичности материалов. На рис. 2.27 представлен примерный вид диаграмм для нескольких материалов.

СЧ
У
с
о

Рис. 2.27. Сравнительные диаграммы растяжения
Сравнивая пределы прочности материалов, можно выделить самый прочный материал, т.е. такой, у которого наибольший предел прочности (диаграмма 4). По величине относительных остаточных удлинений можно судить о пластичности материала. Чем больше 5, тем больше пластичность. Так, к самому пластичному надо отнести материал под номером 2.
По относительному остаточному удлинению все материалы можно разделить на пластичные и хрупкие. Признаком пластичности материала будет служить не наличие площадки текучести, а величина относительных остаточных удлинений. Для хрупких материалов величина 5 не превышает 2…5%, тогда как для пластичных она может достигать порядка 20%.
Однако надо отметить, что деление материалов на хрупкие и пластичные носит условный характер, так как при некоторых условиях хрупкие материалы разрушаются как пластичные, т.е. с большими остаточными деформациями, и наоборот, пластичные — как хрупкие. Например, хрупкий в обычных условиях материал стекло при большом всестороннем сжатии приобретает свойства пластичного материала и разрушается как пластичный. Пластичные стали приобретают хрупкие свойства при низкой температуре. В силу этого точнее было бы говорить о пластичном или хрупком разрушении.
Хотя деление на пластичные и хрупкие материалы все же существует, следует помнить, что речь идет о свойствах материалов при нормальных условиях, т.е. при температуре порядка 20°С и статическом нагружении.
Источник
