Изучение свойств материалов при растяжении
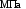
Механические свойства материалов выявляются при испытании их под нагрузкой. Наиболее распространенным видом испытаний являются испытания на растяжение. Это объясняется тем, что мех. свойства мат-лов полученные при испытании на растяжение во многих случаях позволяют достаточно полно судить о поведении материалов при других видах деформации. С другой стороны испытания на растяжении легко осуществимы.
Для испытаний берут образцы стандартных размеров
-общая длина образца
Для стандартных образцов
Чаще всего испытывают образцы диаметром d=1см. Испытания осуществляют на специальных испытательных машинах. Многие машины автоматически вычерчивают графики зависимости нагрузки от деформации.
Ниже рассмотрим диаграмму растяжения малоуглеродистой стали.
Рассмотрим характерные участки и точки этой диаграммы.
На участке ОА деформации растут пропорционально нагрузкам, следовательно до точки А справедлив закон Гука. Точка А соответствует пределу пропорциональности
— предел пропорциональности.
На участке АВ линейная зависимость между Р и нарушается. Однако до точки В возникают в образце упругие деформации. Это означает, если образец нагрузить до точки В, а затем разгрузить, то деформации в образце исчезнут (образец примет первичную форму — предел упругости.
В окрестности точки С имеется почти горизонтальная площадка, здесь деформации растут без видимого увеличения нагрузки. Эта площадка называется площадкой текучести. На поверхности образца появляются наклонные линии. Впервые эти линии заметил русский металлург Чернов. Независимо от него так же заметил Людекс. (Линии Людекса-Чернова)
Точка С – соответствует пределу текучести.
— предел текучести
За площадкой текучести для дальнейшего деформирования образца необходимо увеличить нагрузку.
Точка D – соответствует пределу прочности.
— предел прочности (временного сопротивления).
— наибольшая нагрузка, которую образец выдержал при испытаниях.
Начиная с точки D в образце появляется шейка (местное сужение).
На участке DK деформации растут в районе шейки.
В точке К образец разрушается
, где — напряжение в момент разрушения.
А – площадь поперечного сечения шейки в момент разрушения.
КЕ || ОА
На участке ОЕ возникают остаточные деформации
Замечания:
1) Если образец нагрузить до точки Т, а затем разгрузить, то диаграмма пойдет по линии
TL || OA. При повторном нагружении этого образца карандаш пойдет по линии LTDK.
Как видно в этом случае площадка текучести исчезнет и упругие свойства материала возрастают. Это явление называется наклепоми широко используется в строительстве.
Например арматуру железо-бетонных конструкций предварительно напрягают.
2) Если после разгрузки дать образцу возможность «отдохнуть» (не менее 100 часов) , то при повторном нагружении диаграмма пойдет по линии LTM. Это явление называется явлением старения.
По результатам испытаний можно судить о прочности упругости и пластичности материала.
Прочностьхарактеризуется величинами и
Упругостьхарактеризуется
Пластичностьхарактеризуется и
Где — остаточное относительное удлинение
— относительное сужение.
Где , А – площадь поперечного сечения до деформации, -площадь после деформации.
— для пластичного материала
— для хрупких материалов
Диаграмма напряжений.
Рассмотренная в предыдущем параграфе диаграмма растяжения зависит от размеров образца. Для того чтобы исключить влияние размеров образца на форму диаграммы иногда ее представляют в координатах и
Ниже рассмотрим диаграммы напряжений для некоторых материалов
tg
Из закона Гука известно
— модуль упругости
Диаграмма напряжения хрупкого материала (чугун)
Как видно из рис.2 для хрупких материалов площадка текучести отсутствует, следовательно нет предела текучести. Также видно, что хрупкие материалы при растяжении разрушаются при малых деформациях
Диаграмма растяжения бетона
Испытание на сжатие
Для изучения поведения материалов при сжатии изготавливают образцы цилиндрической формы (для металлов).
Для испытание бетона, камня, дерева берут образцы призматической формы
(для бетона) 20х20х20 для раствора 7,07х7,07х7,07
Как видно из рисунков, малоуглеродистая сталь до предела текучести на сжатие работает так же как и при растяжении.
Предел текучести при сжатии примерно равняется пределу текучести при растяжении.
σсжтек=σ расттек ;
Малоуглеродистая сталь при сжатии не разрушается, образец превращается в диск (нет предела прочности).
Хрупкие материалы: чугун, бетон и т. д на сжатие работают лучше, чем на растяжение, например предел прочности на сжатие чугуна примерно в 4 раза больше предела прочности при растяжении, а у бетона в 8-10 раз.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
Источник
Диаграмма растяжения
Испытание на растяжение выполняют на машинах, развивающих усилие от нескольких килограммов до 2000 тс и более. Стальные образцы на растяжение (рис. 5.1) обычно изготавливают круглого сечения диаметром d, цилиндрическая рабочая часть образца имеет длину не менее /о = 10d.
Рис. 5.1
На рабочей части образца наносятся риски на расстоянии, равном d. Он имеет конические вставки для плавного перехода от рабочей части к головкам, которые предназначены для закрепления образца в захватных приспособлениях машины. Крайние риски на рабочей части образца удалены от конических вставок, это позволяет (как и сами конические вставки) уменьшить влияние концентрации напряжений в месте резкого изменения диаметра на расчётную часть образца.
Зависимость между приложенной нагрузкой F и абсолютной продольной линейной деформацией образца назовём диаграммой растяжения (рис. 5.2). Диаграмма состоит из четырёх зон. Зона ОА — зона упругости, в пределах которой деформации образца упругие, график F — А/ — прямая линия. Зона АВ — площадка текучести, зона общей текучести, в пределах этой зоны интенсивно развиваются пластические деформации при почти постоянной нагрузке. У ряда материалов — легированной стали, бронзы, алюминиевых сплавов — площадки текучести нет (рис. 5.3). Зона ВС — зона упрочнения, в пределах этой зоны увеличивается нагрузка при возрастающей деформации как пластической, так и упругой. В образце намечается место будущего разрыва — зарождается шейка (местное утоныпение образца), рис. 5.4, а.
Рис. 5.2
Рис. 5.3
В зонах общей текучести и упрочнения на поверхности образца из малоуглеродистой стали появляются полосы скольжения — линии Людерса (1859 г.) — Д.К. Чернова (1884 г.); причина их появления — максимальные касательные напряжения, действующие под углом 45° к оси образца (рис. 5.4, б). Зона CD — зона местной текучести, в пределах этой зоны пластические деформации интенсивно развиваются в шейке. Сила, выдерживаемая образцом, уменьшается. Образец разрывается в шейке (рис. 5.4, а).
Рис. 5.4
Если образец в зоне упрочнения разгрузить, то разгрузка произойдет по прямой КМ, параллельной О А. При повторном нагружении на графике F — А/ получим кривую МК (рис. 5.5, а). Область, заключенная между прямой КМ и кривой МК, — петля гистерезиса, которая является свидетельством необратимых потерь энергии на нагрев, на преодоление сил внутреннего трения (рассеивание энергии). Поскольку площадь петли гистерезиса невелика, пренебрегаем ею. Тогда линия повторного нагружения пройдёт по прямой МК (рис. 5.5, б).
На рис. 5.5 стрелками показаны нагружение, разгрузка и последующее нагружение образца. Из рис. 5.5, б следует, что поскольку прямая МК параллельна линии О А, вплоть до точки К образец сохраняет упругие свойства.
Рис. 5.5
На рис. 5.5 обозначены: Д/ост — остаточная абсолютная линейная деформация; А1У — упругая абсолютная линейная деформация, соответствующая точке К диаграммы. Явление повышения упругих свойств материала за счёт предварительного его остаточного (пластического) деформирования назовём наклёпом. Наклёпу подвергают листовую медь прокаткой в холодном состоянии на валках, тросы и цепи — вытяжкой силами выше эксплуатационных. При штамповке тонкостенных конструкций наклёп нежелателен, и его снимают отжигом.
Источник
Для определения свойств материала при
его растяжении и сжатии (до стадии
разрушения) производят механические
испытания образцов в лаборатории.
Материалы по их механическим качествам
можно разделить на две группы:
пластичные и хрупкие. Первые разрушаются
только после значительной
остаточной деформации, хрупкие же — при
весьма малых остаточных
деформациях. К пластичным материалам
относятся: малоуглеродистая
сталь, медь, бронза и др.; к хрупким —
чугун, бетон, камень, кирпич и др.
Один и тот же материал в зависимости от
условий, в которых он находится,
может вести себя и как пластичный и как
хрупкий. Например, «мягкая сталь»
в некоторых случаях сложного
сопротивления, в особенности
при наличии надрезов, иногда ведет себя
как хрупкий материал. Та же
сталь обладает хорошими пластическими
свойствами при нормальной
положительной температуре, а при низкой
(отрицательной)
температуре она приобретает свойства
хрупкости. Таким образом, было бы
правильнее говорить о хрупком и
пластическом состояниях
материалов.
3.6. Испытания материала на растяжение
Образец стандартной формы закрепляют
концами в захваты разрывной
машины. Затем образец растягивают
постепенно возрастающей
нагрузкой без толчков и ударов. В
процессе испытания последовательно
отмечают величины нагрузок и
измеряют соответствующие
им удлинения. Испытательные машины
обычно снабжены специальным
автоматическим приспособлением,
вычерчивающим так называемую
диаграмму растяжения, на которой
по оси ординат величины нагрузок, а
по оси абсцисс — величины абсолютных
удлинений.
Для удобства сравнения результатов
испытания нескольких образцов,
имеющих разные размеры, диаграмму
растяжения обычно перестраивают
в координаты
и(рис. 3.5).
В начальный момент, соответствующий
началу координат диаграммы,
=0
и=0.
При постепенном увеличении нагрузки
стержень получает удлинение,
которое растет прямо пропорционально
силе до точкиAдиаграммы.
ПрямаяOAграфически выражает
закон Гука.
Напряжение, соответствующее крайней
точке AпрямойOA, называется
пределом пропорциональности и обозначается.
Для стали марки Ст. 3=200.
AB— кривая выпуклостью вверх. Прямая
пропорциональность междуинарушена и деформации растут быстрее
напряжений.
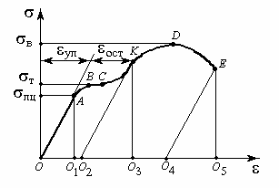
Рис. 3.5
Участок BC— горизонтальная линия —
деформации растут даже без увеличения
нагрузки, и материал, как говорят,
«течет».BC— площадка
текучести материала. Напряжение,
соответствующее точкеB— предел
текучести материала.
Для стали марки Ст. 3=240.
В процессе течения материала на образце
появляются едва заметные
наклонные штрихи под углом около
к его поперечному сечению(штрихи Людерса — Чернова).
Появление этих линий можно объяснить
пластическими деформациями, вызванными
главным образом касательными
напряжениями.
От точки CдоD— пологая кривая.
Помимо упругого удлиненияобразец получает еще значительное
остаточное удлинение.
ТочкаD
соответствует
наибольшему значению нагрузки на
образец. Напряжение, соответствующее
этой точке, называется пределом
прочности
материала, т. е. наибольшим из
возможных для материала напряжением,
отнесенным к первоначальной
площади поперечного сечения образца.
Для стали марки Ст. 3=420.
По достижении наибольшей нагрузки
деформация, приводящая к разрушению,
сосредотачивается в одном месте образца,
в результате чего появляется
сужение его поперечного сечения (шейка),
которая становится
___________________________
Строго говоря, как
показали теоретические (работа А. Надаи)
и экспериментальные
(работа А.Р. Ржаницына) исследования,
штрихи Людерса-Чернова направлены
под углом
к поперечному сечению образца.
все
тоньше и тоньше, и, наконец, при напряжении,
соответствующем точке E,
происходит разрыв.
Деформация, выраженная абсциссой
,
т. е. соответствующая напряжениюявляется упругой деформацией. Она
исчезает после удаления нагрузки.
Если снять нагрузку с образца за
(например, в точкеK), то линия
разгрузки изобразится прямой,
параллельной прямойOA. В данном
случае образец получит кроме упругого
удлинения (отрезок)
и остаточное удлинение (отрезок).
Абсцисса
представляет собой полное удлинение
при напряжении, соответствующем
точкеKдиаграммы.
Таким образом, за пределом пропорциональности
материала относительная деформация
.
Линия
диаграммы параллельна линииOA,
выражающей закон Гука. Следовательно,
и за пределом пропорциональности упругие
деформации пропорциональны
напряжениям.
Для оценки степени пластичности материала
служат величины (в процентах):
— относительное остаточное удлинение
при разрыве (абсцисса);
— относительное остаточное сужение, где- площадь поперечного сечения в месте
разрыва (в шейке);- первоначальная площадь
поперечного сечения.
Чем больше
и,
тем более пластичный материал. Для
обычных сталей8-28
%,30-70
%.
Немного выше, но очень близко к точке Aна диаграмме лежит точка, характеризующая
собой предел упругости материала.
Это напряжение вызывает очень
малые остаточные деформации (порядка
0,001 — 0,005 %), которыми можно пренебречь.
Поэтому практически считают.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛНЕКТРОНИКИ
Кафедра инженерной графики
РЕФЕРАТ на тему:
«Опытное изучение свойств материалов: назначение и виды испытаний. Повышение текучести при повторных нагружениях»
МИНСК, 2008
Для изучения свойств материалов и установления величины предельных напряжений (по разрушению или по пластическим деформациям) производят испытания образцов материала вплоть до разрушения. Испытания производят при нагрузках следующих категорий: статической, ударной и циклической (испытание на усталость или выносливость).
По виду деформации, испытываемой образцом, различают испытания на растяжение, сжатие, кручение и изгиб. Значительно реже проводят испытания на сложное сопротивление, например, сочетание растяжения и кручения.
Так как результаты испытаний зависят от формы образца, скорости его деформирований, температуры при испытании и т. д., то эксперимент обычно ведут в условиях, предусмотренных Государственными стандартами (ГОСТ).
Испытания производят на специальных машинах, разнообразных по конструкции и мощности.
Для измерения деформаций применяют специальные приборы (тензометры), имеющие высокую чувствительность.
Подробное описание испытательных машин и приборов можно найти в специальных руководствах.
Для статического испытания требуется (как минимум) 2 идентичных образца, а для динамического испытания — 3 образца. При испытании на выносливость необходимо иметь 10 идентичных образцов. Для получения более надежных результатов при испытании менее однородных материалов число повторных испытаний следует по возможности увеличивать.
Наибольшее распространение имеют испытания на растяжение статической нагрузкой, так как они наиболее просты и в то же время

во многих случаях дают возможность достаточно верно судить о поведении материала при других видах деформации.
На рис. 2.7 показаны применяемые образцы для испытаний на растяжение. Нормальные цилиндрические образцы имеют диаметр 20 мм и начальную расчетную длину 10 = 10 d0 (длинные образцы) или /0 =5 d0 (короткие образцы). Расчетная длина /0 равна расстоянию между рисками, нанесенными на цилиндрической части образца.
Целью испытания на растяжение является определение механических характеристик материала. При испытании автоматически записывается диаграмма зависимости между растягивающей образец силой Р и удлинением образца Δl.
Для того чтобы можно было сравнивать результаты испытания образцов различных размеров, изготовленных из одинаковых материалов, диаграмму растяжения перестраивают и изображают в другой системе координат: по оси ординат откладывают величину нормального напряжения в поперечном сечении растягиваемого образца , где F0 — первоначальная площадь сечения образца, а по оси абсцисс откладывают относительные удлинения образца, где -первоначальная длина.
Эту диаграмму называют условной диаграммой растяжения (или диаграммой условных напряжений), так как напряжения и относительные удлинения вычисляются соответственно по отношению к первоначальной площади сечения и первоначальной длине образца.

На рис. 2.8 приведена в координатах ε, σ диаграмма растяжения образца из малоуглеродистой стали.
Как видно, вначале на участке ОА до некоторого напряжения σп, называемого пределом пропорциональности, деформации растут пропорционально напряжениям.
Следовательно, до предела пропорциональности сохраняет силу закон Гука. Для стали Ст.З предел пропорциональности σп≈ 2000 кГ/см2 (применяется также обозначение σпц). При дальнейшем увеличении нагрузки диаграмма становится криволинейной.
Однако если напряжения не превосходят определенной величины — предела упругости σу, то материал сохраняет свои упругие свойства, т. е. при разгрузке образец восстанавливает свою первоначальную форму и размеры.
Для стали Ст. 3 предел упругости σу≈2100 кГ/см2. Разница между пределом пропорциональности и пределом упругости невелика, и на практике обычно не делают различия между σп и σу.
Если нагрузку увеличивать еще дальше, то наступает такой момент (точка С), когда деформации начинают расти практически без увеличения нагрузки.
Горизонтальный участок CD диаграммы называется площадкой текучести.
Напряжение, при котором происходит рост деформаций без увеличения нагрузки, называется пределом текучести и обозначается σт.
Для стали Ст.З предел текучести σт≈ 2400 кГ/см2.
Ряд материалов при растяжении дает диаграмму без выраженной площадки текучести; для них устанавливается так называемый условный предел текучести.
Условным пределом текучести называется напряжение, которому соответствует остаточная деформация, равная 0,2%. Условный предел текучести обозначается σ0,2. К материалам, для которых определяется условный предел текучести, относятся дюралюминий, бронза, высокоуглеродистые и легированные стали (например, для стали 37ХНЗА σ0,2 = 10 000 кГ/см2).

Как показывают исследования образцов стали, текучесть сопровождается значительными взаимными сдвигами кристаллов, в результате чего на поверхности образца появляются линии (так называемые линии Людерса — Чернова), наклоненные к оси образца под углом примерно 45° (рис. 2.9, а).
Удлинившись на некоторую величину при постоянном значении силы, т. е. претерпев состояние текучести, материал снова приобретает способность сопротивляться растяжению (упрочняется), и диаграмма за точкой Dподнимается вверх, хотя гораздо более полого, чем раньше (см. рис. 2.8).
Точка Е диаграммы соответствует наибольшему условному напряжению, называемому пределом прочности, или временным сопротивлением.
Для стали Ст.З предел прочности составляет σв = 4000÷5000 кГ/см2 (применяется также обозначение σпч). У высокопрочных сталей величина предела прочности достигает 17 000 кГ/см2 (сталь 40ХНМА и др.). Предел прочности при растяжении обозначается σв. р, при сжатии — σн. с.
При достижении напряжением величины предела прочности на образце появляется резкое местное сужение, так называемая шейка (рис. 2.9, б). Площадь сечения образца в шейке быстро уменьшается и, как следствие, падает усилие и условное напряжение. Разрыв образца происходит по наименьшему сечению шейки.
Кроме перечисленных выше механических характеристик материала, при испытании на растяжение определяют также относительное остаточное удлинение при разрыве δ, являющееся важной характеристикой пластичности материала
(1)
где — первоначальная расчетная длина образца (рис. 2.7);
— расчетная длина образца после разрыва. Она измеряется после стыковки двух частей разорванного образца.

Для стали Ст.З δ≥24%. У высокопрочных сталей эта величина снижается до 7—10%. Величина δ зависит от соотношения между длиной образца и его поперечными размерами. Поэтому в справочниках указывается, на каком образце определялась величина δ. Например, δ 5 обозначает, что удлинение было определено на пятикратном образце, т. е. образце, у которого отношение расчетной длины к диаметру равно пяти.
Определенное таким путем, удлинение является некоторым средним удлинением, так как деформации распределяются по длине образца неравномерно. Наибольшее удлинение возникает в месте разрыва. Оно называется истинным удлинением при разрыве.
Второй характеристикой пластичности материала является относительное остаточное сужение при разрыве
(2)
где F0 — первоначальная площадь поперечного сечения;
F1 — площадь поперечного сечения в наиболее тонком месте шейки после разрыва.
Величина ψ характеризует свойства пластичности более точно, чем δ, поскольку она в меньшей степени зависит от формы образца. Для стали Ст.З значение ψ составляет 50—60%.
Как было отмечено выше, диаграммы растяжения для многих марок стали, а также сплавов, цветных металлов не имеют площадки текучести. Характерный вид диаграммы растяжения для подобных материалов показан на рис. 2.10.
Для изучения значительных пластических деформаций необходимо знать истинную диаграмму растяжения, дающую зависимость между истинными деформациями и истинными напряжениями, которые вычисляются путем деления растягивающей силы на истинную площадь поперечного сечения образца (с учетом сужения).
Так как истинная площадь поперечного сечения меньше первоначальной, то диаграмма истинных напряжений идет выше диаграммы условных напряжений, особенно после образования шейки, когда происходит резкое уменьшение поперечного сечения образца (кривая OCSна рис. 2.8).
Обычно применяют приближенные способы построения диаграммы истинных напряжений, которые излагаются в полных курсах сопротивления материалов.
Рассмотренная диаграмма растяжения (см. рис. 2.8) является характерной для так называемых пластичных материалов, т.е. материалов, способных получать значительные остаточные деформации (δ), не разрушаясь.
Чем пластичнее материал, тем больше δ. К числу весьма пластичных материалов относятся медь, алюминий, латунь, малоуглеродистая сталь и др.
Менее пластичными являются дюраль и бронза, а слабопластичными материалами — большинство легированных сталей.

Противоположным свойству пластичности является хрупкость, т. е. способность материала разрушаться при незначительных остаточных деформациях. Для таких материалов величина остаточного удлинения при разрыве не превышает 2—5%, а в ряде случаев измеряется долями процента. К хрупким материалам относятся чугун, высокоуглеродистая инструментальная сталь, камень, бетон, стекло, стеклопластики и др. Следует отметить, что деление материалов на пластичные и хрупкие является условным, так как в зависимости от условий испытания (скорость нагружения, температура) и вида напряженного состояния хрупкие материалы способны вести себя как пластичные, а пластичные — как хрупкие. Например, чугунный образец в условиях всестороннего сжатия ведет себя как пластичный материал, т.е. не разрушается даже при значительных деформациях. И наоборот, стальной образец с выточкой разрушится при сравнительно небольшой деформации.
Таким образом, правильнее говорить о пластичном и хрупком состояниях материала.
При растяжении образцов из хрупких материалов наблюдается ряд особенностей. Диаграмма растяжения чугуна показана на рис. 2.11. Из диаграммы видно, что отклонение от закона Гука начинается очень рано. Разрыв наступает внезапно при очень малых деформациях и без образования шейки, что характерно для всех хрупких материалов.
При испытании на растяжение хрупких материалов определяют, как правило, только предел прочности. Обычно при практических расчетах для хрупких материалов отклонение от закона Гука не учитывают, т. е. криволинейную диаграмму заменяют условной прямолинейной диаграммой (см. штриховую линию на рис. 2.11).
Для чугуна и других хрупких материалов заметное влияние на предел прочности при разрыве оказывают размеры образца. Это оценивается масштабным коэффициентом
, (3)
где— предел прочности образца диаметром d;
— предел прочности образца диаметром d = 10 мм.
На рис. 2.12 представлены кривые зависимости εв от диаметра образца для следующих материалов: высокоуглеродистая и марганцовистая стали — /, легированная сталь — 2, модифицированный чугун — 3, серый чугун — 4.
Особенно существенно сказывается на величине εв рост абсолютных размеров образца для чугуна (кривые 3 и 4 на рис. 2.12).
Следует отметить, что в последние годы достигнуты значительные успехи в деле создания высокопрочных материалов.
Теоретическое значение предела прочности, вычисленное на основе учета взаимодействия атомов в кристалле, составляет приблизительно одну десятую часть от Е, т.е. для стали примерно 200 000 кГ/см2, что почти в 10 раз больше, чем предел прочности для существующих марок высокопрочных сталей.
К теоретической прочности можно приблизиться двумя путями.
Первый путь — это создание материалов, свободных от внутренних дефектов, имеющих идеальную кристаллическую решетку.
В настоящее время в лабораторных условиях уже получены нитевидные кристаллы («усы») железа и других металлов диаметром 1—2 мкм, в которых полностью отсутствуют внутренние дефекты.
Предел прочности таких «усов» из железа достигает 150 000 кГ/см2.
Другой путь, как это ни парадоксально, прямо противоположен и состоит в создании металлов, имеющих возможно больше нарушений правильной кристаллической структуры. Эти нарушения микроструктуры (дислокации) могут быть получены или сочетанием пластического деформирования металла (наклепа) с термообработкой, или путем нейтронного облучения. При этом из кристаллической решетки выбиваются атомы и в решетке создаются или свободные места — вакансии, или атомы без места — внедренные атомы. Эти нарушения микроструктуры делают металл более прочным, так как затрудняют передвижение внутри кристалла, подобно тому, как шероховатые поверхности двух брусков препятствуют их скольжению.
Если при нагружении образца не был превышен предел упругости, то при разгружении все деформации полностью исчезнут и при повторном нагружении этот образец будет себя вести так же, как и при первом нагружении.
Если же образец был нагружен до напряжения, большего предела упругости, например, до напряжения, соответствующего точке К диаграммы на рис. 2.8, то разгрузка пойдет по прямой KL, параллельной линии О А. Упругая часть деформации (отрезок LM) исчезнет, пластическая же часть деформации (отрезок 0L) останется.
Если материал нагружать снова, то диаграмма пойдет по прямой LKдо самой точки К. Остаточное удлинение при разрыве будет измеряться величиной отрезка LR, т. е. иметь меньшую величину, чем при первичном однократном нагружении до разрыва.
Следовательно, при повторных нагружениях образца, предварительно растянутого до возникновения в нем напряжений, больших предела текучести, предел пропорциональности повышается до того уровня, которого достигли напряжения при предшествующей нагрузке. Если между разгрузкой и повторным нагружением был перерыв, то предел пропорциональности повышается еще больше.
Следует отметить, что диаграмма LKEN, получаемая при повторном нагружении, не имеет площадки текучести, поэтому для образца, претерпевшего разгрузку и повторное нагружение, определяется условный предел текучести (σ0,2), который, очевидно, выше предела текучести при первичном нагружении. В указанном смысле можно говорить о повышении предела текучести при повторном нагружении.
Явление повышения предела пропорциональности и снижения пластичности материала при повторных нагружениях называется наклепом. Наклеп во многих случаях является нежелательным явлением, так как наклепанный металл становится более хрупким.
Однако в целом ряде других случаев наклеп полезен и его создают искусственно, например, в деталях, подвергающихся воздействию переменных нагрузок.
Литература
1 Феодосьев В.И. Сопротивление материалов 2002
2 Беляев Н.М. Сопротивление материалов.1999
3 Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем.1991
4 Работнов Ю.Н. Механика деформируемого твердого тела.2004
5 Степин П.А. Сопротивление материалов.1990
Источник
