Изменение длины тела при растяжении или сжатии прямо пропорционально
Физика, 10 класс
Урок 9. Закон Гука
Перечень вопросов, рассматриваемых на этом уроке
1.Закона Гука.
2.Модели видов деформаций.
3. Вычисление и измерение силы упругости, жёсткости и удлинение пружины.
Глоссарий по теме
Сила упругости – это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.
Деформация – изменение формы или размеров тела, происходящее из-за неодинакового смещения различных частей одного и того же тела в результате воздействия другого тела. Виды деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
Закон Гука – сила упругости, возникающая при деформации тела (растяжение или сжатие пружины), пропорциональна удлинению тела (пружины), и направлена в сторону противоположную направлению перемещений частиц тела
Основная и дополнительная литература по теме:
Г.Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр. 107-112
Рымкевич А.П. Сборник задач по физике. 10-11класс.- М.:Дрофа,2009. Стр 28-29
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Основное содержание урока
В окружающем нас мире мы наблюдаем, как различные силы заставляют тела двигаться, делать прыжки, перемещаться, взаимодействовать.
Однако можно также наблюдать как происходят разрушения, так называемые деформации, различных сооружений: мостов, домов, разнообразных машин.
Что необходимо знать инженеру конструктору, строителю, чтобы строить надёжные сооружения: дома, мосты, машины?
Почему деформации различны, какие виды деформации могут быть у конкретных тел? Почему одни тела после деформации могут восстановиться, а другие нет? От чего зависит и можно ли рассчитать величину этих деформаций?
Деформация — это изменение формы или размеров тела, в результате воздействия на него другого тела.
Почему деформации не одинаковы у различных тел, если мы их, к примеру, сжимаем? Давайте вспомним что мы знаем о строении вещества.
Все вещества состоят из частиц. Между этими частицами существуют силы взаимодействия- эти силы электромагнитной природы. Эти силы в зависимости от расстояний между частицами проявляются, то как силы притяжения, то как силы отталкивания.
Сила упругости – сила, возникающая при деформации любых тел, а также при сжатии жидкостей и газов. Она противодействует изменению формы тел.
Мы можем наблюдать несколько видов деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
При деформации растяжения межмолекулярные расстояния увеличиваются. Такую деформацию испытывают струны в музыкальных инструментах, различные нити, тросы, буксирные тросы.
При деформации сжатия межмолекулярные расстояния уменьшаются. Под такой деформацией находятся стены, фундаменты сооружений и зданий.
При деформации изгиба происходят неординарные изменения, одни межмолекулярные слои увеличиваются, а другие уменьшаются. Такие деформации испытывают перекрытия в зданиях и мостах.
При кручении – происходят повороты одних молекулярных слоёв относительно других. Эту деформацию испытывают: валы, витки цилиндрических пружин, столярный бур, свёрла по металлу, валы при бурении нефтяных скважин. Деформация среза тоже является разновидностью деформации сдвига.
Первое научное исследование упругого растяжения и сжатия вещества провёл английский учёный Роберт Гук.
Роберт Гук установил, что при малых деформациях растяжения или сжатия тела абсолютное удлинение тела прямо пропорционально деформирующей силе.
F упр = k ·Δℓ = k · Iℓ−ℓ0I закон Гука.
k− коэффициент пропорциональности, жёсткость тела.
ℓ0 — начальная длина.
ℓ — конечная длина после деформации.
Δℓ = I ℓ−ℓ₀ I- абсолютное удлинение пружины.
— единица измерения жёсткости в системе СИ.
При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе, а слишком большие деформации разрушают тело.
Для расчёта движения тел под действием силы упругости, нужно учитывать направление этой силы. Если принять за начало отсчёта крайнюю точку недеформированного тела, то абсолютное удлинение тела можно характеризовать конечной координатой деформированного тела. При растяжении и сжатии сила упругости направлена противоположно смещению его конца.
Закон Гука можно записать для проекции силы упругости на выбранную координатную ось в виде:
F упр x = − kx — закона Гука.
k – коэффициент пропорциональности, жёсткость тела.
x = Δℓ = ℓ−ℓ0 удлинение тела (пружины, резины, шнура, нити….)
Fупр x = − kx
Закон Гука:
Fупр = k·Δℓ = k · Iℓ−ℓ0I
Графиком зависимости модуля силы упругости от абсолютного удлинения тела является прямая, угол наклона которой к оси абсцисс зависит от коэффициента жёсткости k. Если прямая идёт круче к оси силы упругости, то коэффициент жёсткости этого тела больше, если же уклон прямой идёт ближе к оси абсолютного удлинения, следует понимать, что жёсткость тела меньше.
График, зависимости проекции силы упругости на ось ОХ, того же тела от значения х.
Необходимо помнить, что закон Гука хорошо выполняется при только при малых деформациях. При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе.
Разбор тренировочных заданий
1. По результатам исследования построен график зависимости модуля силы упругости пружины от её деформации. Чему равна жёсткость пружины? Каким будет удлинение этой пружины при подвешивании груза массой 2кг?
Решение: По графику идёт линейная зависимость модуля силы упругости и удлинение пружины. Зависимость физических величин по Закону Гука:
F упр x = − kx (1)
Fупр =k·Δℓ = k · Iℓ−ℓ0I (2)
Из формулы (1) выражаем:
Зная что Fт = mg = 20 Н, Fт = Fупр= k·Δℓ следовательно
Ответ: жёсткость пружины равна 200 Н/м, удлинение пружины равно 0,1м.
2. К системе из кубика массой 1 кг и двух пружин приложена постоянная горизонтальная сила. Система покоится. Между кубиком и опорой трения нет. Левый край первой пружины прикреплён к стенке. Удлинение первой пружины 0,05 м. Жёсткость первой пружины равна 200 Н/м. Удлинение второй пружины 0,25 м.
- Чему равна приложенная к системе сила?
- Чему равна жёсткость второй пружины?
- Во сколько раз жёсткость второй пружины меньше чем первой?
Решение:
1. По условию задачи система находится в покое. Зная жёсткость и удлинение пружины найдём силу, которая уравновешивает приложенную постоянную горизонтальную силу.
F = F упр =k1·Δℓ1= 200 Н/м·0,05 м = 10 Н
2. Жёсткость второй пружины:
3. k1/ k2 = 200/40 = 5
Ответ: F=10 Н; k2 = 40 Н/м; k1/k2 = 5.
Источник
Глава 2. Взаимодействие тел
Вам уже известно, что на все тела, находящиеся на Земле, действует сила тяжести. В результате действия силы тяжести на Землю падает подброшенный камень, выпущенная из лука стрела, снежинки, листья, оторвавшиеся от веток, и др.
На книгу, лежащую на столе, также действует сила тяжести, но книга не проваливается сквозь стол, а находится в покое. Подвесим тело на нити. Оно падать не будет.
Почему же покоятся тела, лежащие на опоре или подвешенные на нити? По-видимому, сила тяжести уравновешивается какой-то другой силой. Что же это за сила и как она возникает?
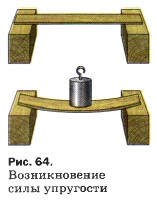
Проведём опыт. На середину горизонтально расположенной доски поставим гирю (рис. 64). Под действием силы тяжести гиря начнёт двигаться вниз и прогнёт доску, т. е. доска деформируется. При этом возникает сила, с которой опора (доска) действует на тело, расположенное на ней. Из этого опыта можно сделать вывод, что на гирю, кроме силы тяжести, направленной вертикально вниз, действует ещё какая-то другая сила. Эта сила направлена вертикально вверх. Она и уравновесила силу тяжести. Эту силу называют силой упругости.
- Сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение, называется силой упругости.
Силу упругости обозначают буквой F с индексом: Fynp.
Чем сильнее прогибается опора (доска), тем больше сила упругости. Если сила упругости становится равной силе тяжести, действующей на тело, прогибание доски прекращается.
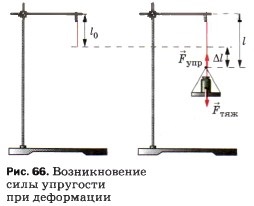
Теперь подвесим тело на нити. Нить (подвес) растягивается (рис. 65). В нити (подвесе), также как и в опоре, возникает сила упругости. При растяжении подвеса сила упругости увеличивается. Если сила упругости будет равна силе тяжести, то растяжение прекращается. Сила упругости возникает только при деформации тел. Если исчезает деформация тела, то исчезает и сила упругости.
Деформации бывают разных видов: растяжения, сжатия (см. рис. 56), сдвига, изгиба (см. рис. 64), кручения.
Теперь попытаемся выяснить, от чего зависит сила упругости.
Английский учёный Роберт Гук, современник Ньютона, установил, как зависит сила упругости от деформации.
Рассмотрим опыт. Возьмём резиновый шнур. Один конец его закрепим в штативе (рис. 66). Первоначальная длина шнура к свободному концу шнура подвесить чашку с гирькой, то шнур удлинится. Его длина станет равной Удлинение шнура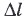 
(Δ — греч. буква «дельта») можно найти так:
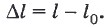
Если менять гирьки на чашке, то будет меняться и длина шнура, а значит, его удлинение (деформация) .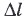
Опыт показал, что изменение длины тела при растяжении (или сжатии) прямо пропорционально модулю силы упругости.
В этом и заключается закон Гука. Записывается закон Гука следующим образом:
где 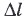— удлинение тела (изменение его длины), k — коэффициент пропорциональности, который называется жёсткостью.
Жёсткость тела зависит от формы и размеров, а также от материала, из которого оно изготовлено.
Закон Гука справедлив только для упругой деформации. Если после прекращения действия сил, деформирующих тело, оно возвращается в исходное положение, то деформация является упругой.
Вопросы
1. Когда возникает сила упругости?
2. Что называют деформацией тела?
3. Какие виды деформаций вы знаете?
4. Как формулируется закон Гука?
5. От чего зависит сила упругости?
Источник
Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие
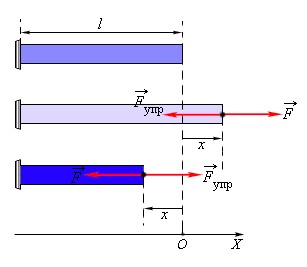
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Закон Гука
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k — коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
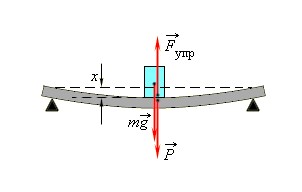
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр.
Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.
Источник
Çàêîí Ãóêà ÿâëÿåòñÿ îñíîâíûì çàêîíîì òåîðèè óïðóãîñòè, êîòîðûé ãëàñèò: ñèëà óïðóãîñòè, âîçíèêàþùàÿ ïðè óïðóãîé äåôîðìàöèè òåëà (ðàñòÿæåíèè èëè ñæàòèè ïðóæèíû) ïðîïîðöèîíàëüíà óäëèíåíèþ òåëà (ïðóæèíû) è íàïðàâëåíà â ñòîðîíó, ïðîòèâîïîëîæíóþ íàïðàâëåíèþ ïåðåìåùåíèé ÷àñòèö òåëà ïðè äåôîðìàöèè.
Åñëè îáîçíà÷èòü óäëèíåíèå òåëà ÷åðåç x, à ñèëó óïðóãîñòè ÷åðåç Fóïð, òî çàêîí Ãóêà ìîæíî ïðåäñòàâèòü â âèäå ôîðìóëû:
Fóïð = — kx,
ãäå k – êîýôôèöèåíò ïðîïîðöèîíàëüíîñòè, íàçûâàåìûé æåñòêîñòüþ òåëà. Çíàê ìèíóñ óêàçûâàåò íà òî, ÷òî ñèëû óïðóãîñòè è óäëèíåíèÿ x ïðîòèâîïîëîæíû. Åäèíèöåé æåñòêîñòè â ÑÈ ÿâëÿåòñÿ íüþòîí íà ìåòð (1 Í/ì). Ñèëà óïðóãîñòè Fóïð (â çàêîíå Ãóêà), êàê è ëþáàÿ äðóãàÿ ñèëà, èçìåðÿåòñÿ â Íüþòîíàõ, îáîçíà÷àåòñÿ êàê Í.
Êàæäîå òåëî èìååò ñâîþ æåñòêîñòü è ÷åì îíà áîëüøå, òåì ìåíüøå îíî èçìåíÿåò ñâîþ äëèíó ïîä äåéñòâèåì äàííîé ñèëû.
Íåîáõîäèìî ïîìíèòü, ÷òî çàêîí Ãóêà ïðèìåíèì òîëüêî äëÿ óïðóãîé äåôîðìàöèè. Çàêîí Ãóêà âûïîëíÿåòñÿ òîëüêî ïðè ìàëûõ äåôîðìàöèÿõ. Ïðè áîëüøèõ äåôîðìàöèÿõ èçìåíåíèå äëèíû ïåðåñòàåò áûòü ïðÿìî ïðîïîðöèîíàëüíûì ïðèëîæåííîé ñèëå, à ñëèøêîì áîëüøèå äåôîðìàöèè ðàçðóøàþò òåëî.
Êàëüêóëÿòîðû ïî ôèçèêå | |
| Ðåøåíèå çàäà÷ ïî ôèçèêå, ïîäãîòîâêà ê ÝÃÅ è ÃÈÀ, ìåõàíèêà òåðìîäèíàìèêà è äð. | |
| Êàëüêóëÿòîðû ïî ôèçèêå | |
Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ôèçèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Êâàíòîâàÿ ôèçèêà. | |
| Êâàíòîâàÿ ôèçèêà ÿâëÿåòñÿ ðàçäåëîì òåîðåòè÷åñêîé ôèçèêè, èçó÷àþùåãî êâàíòîâî-ìåõàíè÷åñêèå è êâàíòîâî-ïîëåâûå ñèñòåìû, à òàêæå çàêîíû èõ äâèæåíèÿ. | |
| Êâàíòîâàÿ ôèçèêà. | |
Êèíåìàòèêà. Ïîñòóïàòåëüíîå äâèæåíèå. | |
| Ïîñòóïàòåëüíîå äâèæåíèå – ýòî äâèæåíèå òâåðäîãî òåëà, ïðè êîòîðîì ïðÿìàÿ, ñîåäèíÿþùàÿ äâå ëþáûå òî÷êè òåëà, îñòàåòñÿ ïàðàëëåëüíîé ñàìîé ñåáå. | |
| Êèíåìàòèêà. Ïîñòóïàòåëüíîå äâèæåíèå. | |
Çàêîí âñåìèðíîãî òÿãîòåíèÿ â äèíàìèêå. | |
| Çàêîí âñåìèðíîãî òÿãîòåíèÿ áûë îòêðûò âåëèêèì àíãëèéñêèì ó÷åíûì Èñààêîì Íüþòîíîì è ãëàñèò: ñèëà , ñ êîòîðîé äâå ìàòåðèàëüíûå òî÷êè ñ ìàññàìè m 1 è m 2 ïðèòÿãèâàþò äðóã äðóãà, ïðîïîðöèîíàëüíà ìàññàì ýòèõ òî÷åê è îáðàòíî ïðîïîðöèîíàëüíà êâàäðàòó ðàññòîÿíèÿ r 2 ìåæäó íèìè. | |
| Çàêîí âñåìèðíîãî òÿãîòåíèÿ â äèíàìèêå. | |
Çàêîí Êóëîíà. | |
| Çàêîí Êóëîíà — ýòî îäèí èç îñíîâíûõ çàêîíîâ ýëåêòðîñòàòèêè . | |
| Çàêîí Êóëîíà. | |
Источник
Законом Гука называют базовую зависимость в механике, устанавливающую взаимосвязь между усилиями и соответствующими им упругими деформациями.
Закон был открыт в 1660 году английским ученым Робертом Гуком.
Проведя серию экспериментов с растяжением и сжатием пружин, Гук заметил, что изменение их длины прямо пропорционально растягивающей (сжимающей) их силе.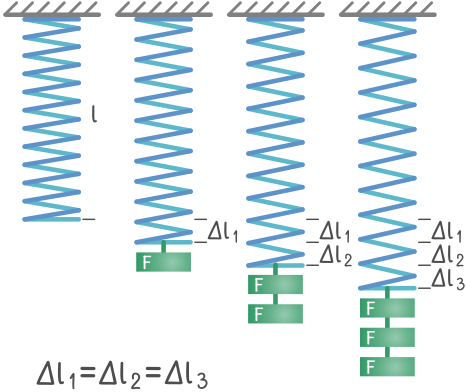
Свои наблюдения он оформил в виде закона: «Какова сила, таково и удлинение».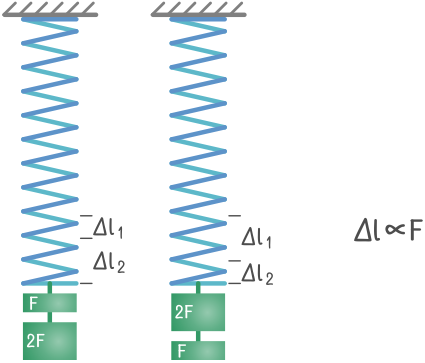
Современная формулировка закона существенно отличается от оригинала и зависит от дисциплины, в которой рассматривается зависимость деформаций от усилий.
Подробнее про закон Гука смотрите в нашем видео:
Закон Гука в физике
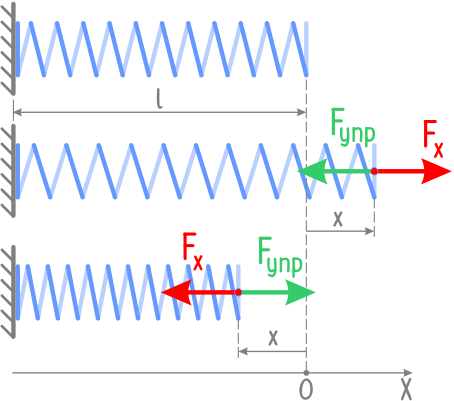
В современных учебниках физики Закон Гука имеет вид: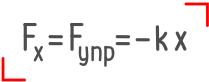
и формулируется следующим образом:
«При малых деформациях сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения его частиц»
Коэффициент k характеризует жесткость образца и зависит от его размеров и материала.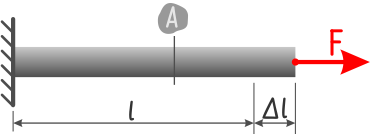
Например, для стержней, работающих на растяжение или сжатие, он может быть рассчитан по формуле: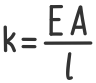
где:
E – Модуль упругости I рода (модуль Юнга);
A – Площадь поперечного сечения бруса;
l – Длина стержня.
Знак минус означает, что силы упругого сопротивления направлены обратно растягивающей силе.
Закон Гука в сопромате
В технической механике и сопротивлении материалов в частности закон Гука гласит: «До определенного момента, называемого пределом пропорциональности, упругие деформации прямо пропорциональны напряжениям».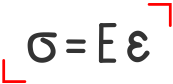
Здесь:
σ — Нормальные напряжения в сечении;
ε — Относительные продольные деформации.
Рассмотрим преобразование физической формы закона к его механическому виду.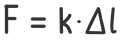
Подставим вместо коэффициента k его выражение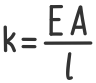
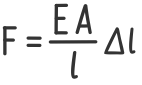
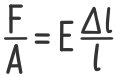
Отношение продольной силы F к площади поперечного сечения A в левой части дает нормальные напряжения в сечении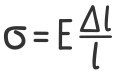
Отношение абсолютных деформаций к начальной длине образца – это относительное изменение его длины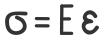
В таком виде закон Гука используется в сопромате и технической механике.
Закон выполняется только для напряжений не превышающих предела пропорциональности.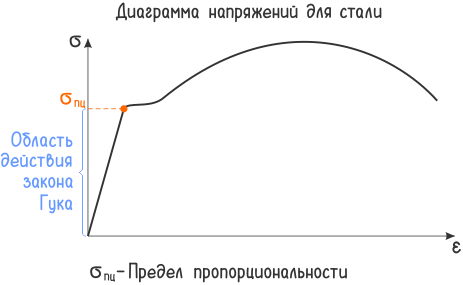
При растяжении и сжатии
При растяжении и сжатии закон Гука можно получить, вернув в его канонический вид геометрические параметры стержня (длину и площадь поперечного сечения), и записав получившееся выражение относительно линейной деформации: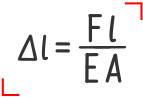
Здесь
Δl- Абсолютная деформация стержня;
F — Продольная сила;
l — Длина стержня до нагружения;
E – Модуль продольной упругости материала;
A – Площадь поперечного сечения стержня.
При изгибе
При изгибе закон устанавливает зависимость между кривизной продольной оси и величиной изгибающего момента в соответствующем сечении балки.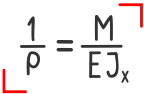
где:
ρ — Радиус кривизны продольной оси балки в данном сечении;
M — Величина соответствующего внутреннего изгибающего момента;
E – Модуль Юнга;
Ix — Осевой момент инерции поперечного сечения балки.
Обобщенный закон Гука
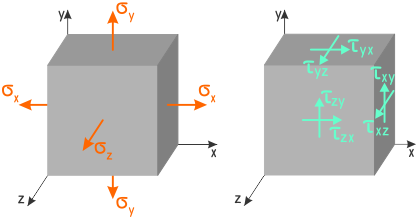
Для общего случая нагружения изотропных материалов, когда напряженное состояние отличается от линейного (одноосного) применяется закон Гука в обобщённом виде.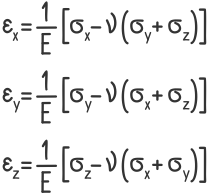
ε — Относительные деформации вдоль соответствующих осей;
ν — Коэффициент Пуассона;
σ — Нормальные напряжения по соответствующим площадкам элемента.
Потому что деформации в поперечных направлениях тоже влияют на изменение продольных размеров.
Для чистого сдвига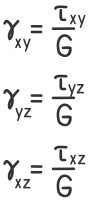
γ — Угловое перемещение соответствующей площадки элемента;
τ — Касательные напряжения;
G — Модуль упругости II рода (модуль сдвига).
Испытание на растяжение >>
Диаграмма напряжений >>
Источник