Испытание материалов при одноосном растяжении
Лабораторная работа № 1
Цель работы – изучить поведение малоуглеродистой стали при растяжении и определить ее механические характеристики.
Основные сведения
Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.
Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.
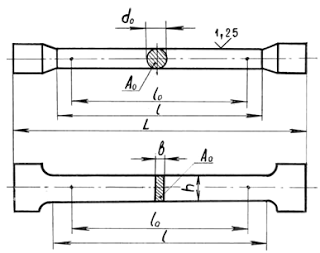
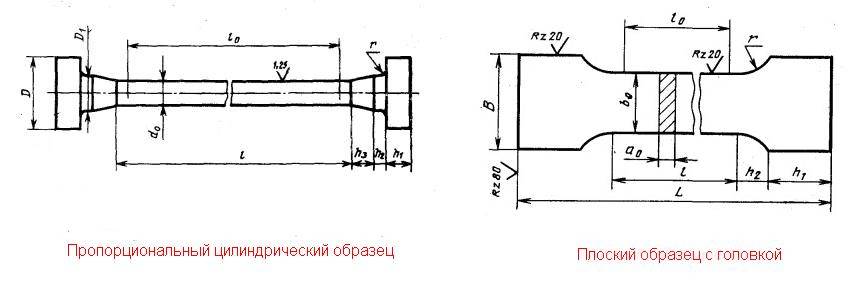
В таких случаях, кроме металлографических исследований, определяются главные механические характеристики на образцах, взятых из зоны разрушения конструкции. Образцы изготавливаются по ГОСТ 1497-84 и могут иметь различные размеры и форму (рис. 1.1).
Рис. 1.1. Образцы для испытания на растяжение
Между расчетной длиной образца lо и размерами поперечного сечения Ао (или dо для круглых образцов) выдерживается определенное соотношение:
В испытательных машинах усилие создается либо вручную — механическим приводом, либо гидравлическим приводом, что присуще машинам с большей мощностью.
В данной работе используется универсальная испытательная машина УММ-20 с гидравлическим приводом и максимальным усилием 200 кН, либо учебная универсальная испытательная машина МИ-40КУ (усилие до 40 кН).
Порядок выполнения и обработка результатов
Образец, устанавливаемый в захватах машины, после включения насоса, создающего давление в рабочем цилиндре, будет испытывать деформацию растяжения. В измерительном блоке машины есть шкала с рабочей стрелкой, по которой мы наблюдаем рост передаваемого усилия F.
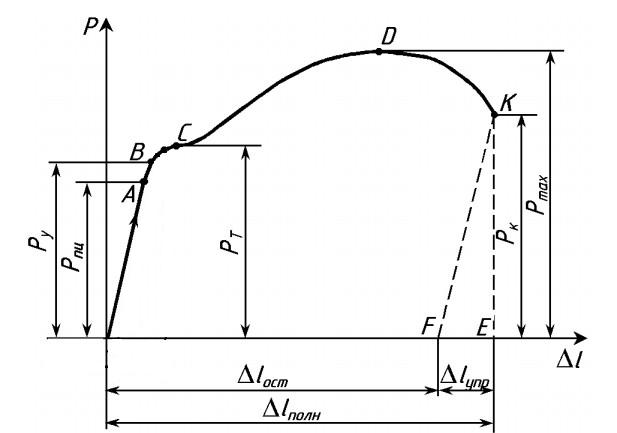
Зависимость удлинения рабочей части образца от действия растягивающей силы во время испытания отображается на миллиметровке диаграммного аппарата в осях F-Δl (рис. 1.2).
В начале нагружения деформации линейно зависят от сил, потому участок I диаграммы называют участком пропорциональности. После точки В начинается так называемый участок текучести II.
На этой стадии стрелка силоизмерителя как бы спотыкается, приостанавливается, от точки В на диаграмме вычерчивается либо прямая, параллельная горизонтальной оси, либо слегка извилистая линия — деформации растут без увеличения нагрузки. Происходит перестройка структуры материала, устраняются нерегулярности в атомных решетках.
Далее самописец рисует участок самоупрочнения III. При дальнейшем увеличении нагрузки в образце происходят необратимые, большие деформации, в основном концентрирующиеся в зоне с макронарушениями в структуре – там образуется местное сужение — «шейка».
На участке IV фиксируется максимальная нагрузка, затем идет снижение усилия, ибо в зоне «шейки» сечение резко уменьшается, образец разрывается.
При нагружении на участке I в образце возникают только упругие деформации, при дальнейшем нагружении появляются и пластические — остаточные деформации.
Если в стадии самоупрочнения начать разгружать образец (например, от т. С), то самописец будет вычерчивать прямую СО1. На диаграмме фиксируются как упругие деформации Δlу (О1О2), так и остаточные Δlост (ОО1). Теперь образец будет обладать иными характеристиками.
Так, при новом нагружении этого образца будет вычерчиваться диаграмма О1CDЕ, и практически это будет уже другой материал. Эту операцию, называемую наклеп, широко используют, например, в арматурных цехах для улучшения свойств проволоки или арматурных стержней.
Диаграмма растяжения (рис. 1.2) характеризует поведение конкретного образца, но отнюдь не обобщенные свойства материала. Для получения характеристик материала строится условная диаграмма напряжений, на которой откладываются относительные величины – напряжения σ=F/A0 и относительные деформации ε=Δl/l0 (рис. 1.3), где А0, l0 – начальные параметры образца.
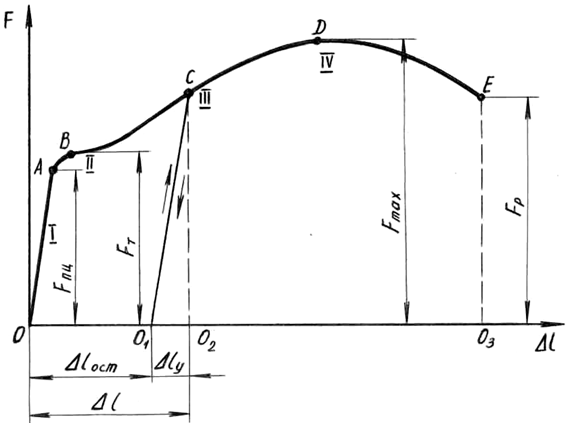
Рис. 1.2. Диаграмма растяжения образца из малоуглеродистой стали
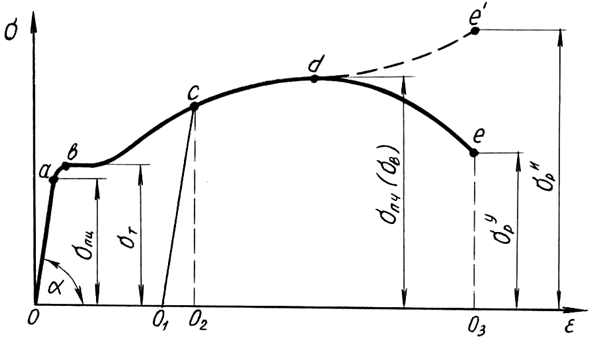
Рис. 1.3. Условная диаграмма напряжений при растяжении
Условная диаграмма напряжений при растяжении позволяет определить следующие характеристики материала (рис. 1.3):
σпц – предел пропорциональности – напряжение, превышение которого приводит к отклонению от закона Гука. После наклепа σпц может быть увеличен на 50-80%;
σу – предел упругости – напряжение, при котором остаточное удлинение достигает 0,05%. Напряжение σу очень близко к σпц и обнаруживается при более тонких испытаниях. В данной работе σу не устанавливается;
σт – предел текучести – напряжение, при котором происходит рост деформаций при постоянной нагрузке.
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют ≈0,2% (рис. 1.4);
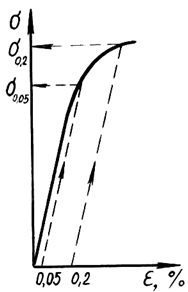
Рис. 1.4. Определение предела упругости и условного предела текучести
σпч (σв) – предел прочности (временное сопротивление) – напряжение, соответствующее максимальной нагрузке;
σр – напряжение разрыва. Определяется условное σур и истинное σир=Fр/Аш, где Аш – площадь сечения «шейки» в месте разрыва.
Определяются также характеристики пластичности – относительное остаточное удлинение
δ = (l1 – l0)∙100% / l0,
где l1 – расчетная длина образца после разрыва,
и относительное остаточное сужение
ψ = (А0 — Аш)∙100% / А0.
По диаграмме напряжений можно приближенно определить модуль упругости I рода
E=σпц/ε=tgα,
причем после операции наклепа σпц возрастает на 20-30%.
Работа, затраченная на разрушение образца W, графически изображается на рис. 1.2 площадью диаграммы OABDEO3. Приближенно эту площадь определяют по формуле:
W = 0,8∙Fmax∙Δlmax.
Удельная работа, затраченная на разрушение образца, говорит о мере сопротивляемости материала разрушению w = W/V, где V = A0∙l0 – объем рабочей части образца.
По полученным прочностным и деформационным характеристикам и справочным таблицам делается вывод по испытуемому материалу о соответствующей марке стали
Контрольные вопросы
- Изобразите диаграмму растяжения образца из малоуглеродистой стали (Ст.3). Покажите полные, упругие и остаточные абсолютные деформации при нагружении силой, большей, чем Fт.
- На каком участке образца происходят основные деформации удлинения? Как это наблюдается на образце? Какие нагрузки фиксируются в этот момент?
- Объясните, почему после образования шейки дальнейшее растяжение происходит при все уменьшающейся нагрузке?
- Перечислите механические характеристики, определяемые в результате испытаний материала на растяжение. Укажите характеристики прочности и пластичности.
- Дайте определение предела пропорциональности.
- Дайте определение предела упругости.
- Дайте определение предела текучести.
- Дайте определение предела прочности.
- Как определить предел текучести при отсутствии площадки текучести? Покажите, как это сделать, по конкретной диаграмме.
- Какие деформации называются упругими, какие остаточными? Укажите их на полученной в лабораторной работе диаграмме растяжения стали.
- Как определяется остаточная деформация после разрушения образца?
- Выделите на диаграмме растяжения образца из мягкой стали упругую часть его полного удлинения для момента действия максимальной силы.
- Какое явление называется наклепом? До какого предела можно довести предел пропорциональности материалов с помощью наклепа?
- Как определяется работа, затраченная на разрушение образца? О каком свойстве материала можно судить по удельной работе, затраченной на разрушение образца?
- Как определить марку стали и допускаемые напряжения для нее после проведения лабораторных испытаний?
- Чем отличается диаграмма истинных напряжений при растяжении от условной диаграммы?
- Можно ли определить модуль упругости материала по диаграмме напряжений?
- Как определить работу, затрачиваемую на деформации текучести лабораторного образца?
Испытание материалов на сжатие >
Краткая теория >
Примеры решения задач >
Источник
Основным видом исследования механических свойств материалов является испытание на растяжение. Оно проводится на специальных испытательных машинах, создающих постепенно возрастающую нагрузку на испытываемый образец и осуществляющих в процессе нагружения регистрацию величины действующей на образец силы и его деформации.
Чаще всего применяют цилиндрические образцы (рис. 2.1, а), а при испытании листового материала – плоские (рис. 2.1, б).
Для цилиндрических образцов выдерживают определенное соотношение между расчетной длиной образца l0 и диаметром образца d0..Обычно l0 = 10 d0(длинный образец); реже l0 = 5d0 (короткий образец). Учитывая, что диаметр d0связан с площадью сечения образца формулой
,
связь между расчетной длиной l0 и площадью поперечного сечения образца можно выразить для длинного (десятикратного) образца зависимостью
, (2.1)
для короткого (пятикратного)
. (2.2)
Рисунок 2.1 – Цилиндрические (а) и плоские (б) образцы для испытания на растяжение
В качестве основных образцов при испытании на растяжение применяют цилиндрические образцы с диаметром d0 = 10 мм, расчетной длиной l0 = 100 мм и l0 = 50 мм. Допускается применение и других пропорциональных образцов, в которых выдержаны соотношения размеров в соответствии с формулами (2.1, 2.2).
Образец перед испытанием измеряется штангенциркулем и устанавливается в захваты испытательной машины, где к нему прикладывается осевая статическая нагрузка. Под действием приложенной силы образец удлиняется; с ростом силы растет и удлинение.
Специальное устройство, так называемый диаграммный аппарат, вычерчивает в определенном масштабе кривую в координатах Р.- , называемую диаграммой растяжения (первичная диаграмма)), вид которой зависит от свойств материала и размеров образца. Для малоуглеродистых сталей (сталь Ст2, Ст3 и др.) диаграмма имеет вид, показанный на рис. 2.2.
Из рисунка видно, что диаграмма имеет ряд характерных точек (1…5), соответствующих определенному состоянию металла образца.
На начальном участке диаграммы О-1 наблюдается линейная зависимость между силой Р и удлинением образца , т.е. деформируется материал упруго и подчиняется закону Гука. При дальнейшем увеличении силы (участок 1-2) закон Гука нарушается, однако материал деформируется упруго, поэтому, если разгрузить образец с точки 2, то перо записи диаграммы возвращается в начало координат.
Рисунок. 2.2 – Диаграмма растяжения (первичная диаграмма)
Участок 2-3 именуется площадкой текучести, т.к. здесь наблюдается пластическое течение материала (необратимое) при постоянной нагрузке. На этом участке металл переходит в новое качественное состояние. На гладкой полированной поверхности образца появляется сетка линий скольжения (так называемые линии Чернова–Людерса) – следствие сдвигов по плоскостям наибольших касательных напряжений. Линии скольжения составляют угол 45° с продольной осью образца;
Дальнейшее деформирование образца от точки 3 до точки 4 требует увеличения силы Р, причем зависимость между Р и становится нелинейной. В точке 4 усилие растяжения достигает своего наибольшего значения – Рmax. Материал на рассматриваемом участке упрочняется за счет явления наклепа.
От точки О до точки 4 образец на всей рабочей части равномерно удлиняется с соответствующим равномерным уменьшением сечения (диаметра).
Начиная с точки 4 растяжение образца приведет к образованию местного сужения (именуемое «шейкой»), кривая на диаграмме идет вниз и на точке 5 обрывается (образец разрушается в «шейке»).
Следует отметить, что разгрузка образца с любой точки диаграммы (напр. точки i) на участке диаграммы 2-5 приведет к исчезновению только упругой деформации (отрезок ), но останутся пластические (отрезок ОО1), и перо записи диаграммы уже не возвратится в начало координат, т.е. образец получит остаточное удлинение.
Вид разрушенного путем растяжения образца показан на рис. 2.3.
Пользуясь указанными характерными нагрузками, взятыми из диаграммы растяжения, и зная площадь сечения испытуемого образца , определяют основные характеристики прочности материала:
Источник
Испытание на растяжение металла заключаются в растяжении образца с построением графика зависимости удлинения образца (Δl) от прилагаемой нагрузки (P), с последующим перестроением этой диаграммы в диаграмму условных напряжений (σ — ε)
Испытания на растяжение проводятся по ГОСТ 1497, по этому же ГОСТу определяются и образцы на которых проводятся испытания.
Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
- Участок ОА — участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
- Участок ОВ — участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении
Выше точки В диаграмма растяжения отходит от прямой — деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.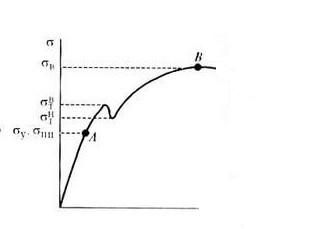
Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение — шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.
Прилагаемая нагрузка для растяжения образца зависит от геометрии этого образца. Чем больше площадь сечения, тем более высокая нагрузка необходима для растяжения образца. По этой причине, получаемая машинная диаграмма не дает качественной оценки механических свойств материала. Чтобы исключить влияние геометрии образца, машинную диаграмму перестраивают в координатах σ − ε путем деления ординат P на первоначальную площадь сечения образца A0 и абсцисс ∆l на lо. Перестроенная таким образом диаграмма называется диаграммой условных напряжений. Уже по этой, новой диаграмме, определяют механические характеристики материала.
Определяются следующие механические характеристики:
Предел пропорциональности σпц – наибольшее напряжение, после которого нарушается справедливость закона Гука σ = Еε , где Е – модуль продольной упругости, или модуль упругости первого рода. При этом Е =σ/ε = tgα , т. е. модуль E это тангенс угла наклона прямолинейной части диаграммы к оси абсцисс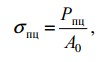
Предел упругости σу — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σу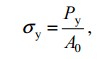
Предел текучести σт – напряжение, при котором происходит увеличение деформации без заметного увеличения растягивающей нагрузки
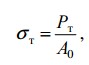Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести
Предел прочности (временное сопротивление разрыву) σв – напряжение, соответствующее наибольшей нагрузке Pmax , предшествующей разрыву образца
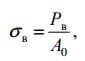
Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности — относительное удлинение δ и относительное сужение ψ
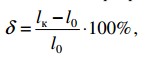
где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца
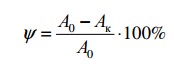
Источник
В этих испытаниях образец стандартной формы (в виде прутка с утолщениями на торцах) закрепляется в зажимах разрывной машины и к его концам прикладывается плавно нарастающая, растягивающая сила F.
F S0 F
l0
где S0 — начальная площадь поперечного сечения прутка, l0 — начальная длина.
В процессе испытания измеряется относительное удлинение образца или иначе его деформация εв %, а также напряжение в образце σв МПа:
, (4.2)
В результате получают диаграмму растяжения материала, то есть график зависимости напряжения от деформации.
Рассмотрим типичную для металлов диаграмму растяжения.
Рис.4.2. Диаграмма растяжения материала
На данной диаграмме выделяются 4 характерных участка: ОА, АВ, ВС и СD. Участок ОА (намерено увеличенный для наглядности) соответствует упругой деформации. На этом участке наблюдается линейная зависимость напряжения от деформации, то есть . Разгрузка образца здесь происходит по той же линии ОА, но в обратном направлении. Когда напряжение становится равным нулю (σ = 0) деформация полностью исчезает (ε= 0).
Коэффициент пропорциональности Е называют модулем упругости. Его величина характеризует жёсткость материала. Чем больше Е, тем круче участок ОА и, соответственно, выше жёсткость материала.
При напряжении σT нарушается пропорциональность между деформацией и напряжением. Наряду с упругой деформацией появляется пластическая составляющая. Напряжение σT называют пределом текучести. У некоторых пластичных металлов при этом напряжении на диаграмме растяжения наблюдается горизонтальный участок АВ (площадка текучести), на котором пластическая деформация образца происходит без заметного повышения напряжения. В этом случае предел текучести является реальным, физически фиксируемым. Для тех материалов, у которых такой площадки не наблюдается, используют условный предел текучести σ0,2 — это такое напряжение, при котором остаточная пластическая деформация составляет величину 0,2%.
Если напряжение на образце превышает предел текучести (точка F), то деформация образца имеет две составляющие: e = eУПР + eОСТ.Разгрузка образца в таком случае происходит не по линии нагрузки, а по линии FG, параллельной участку ОА. При этом упругая составляющая деформации исчезает, а пластическая сохраняется.
В точке С наблюдается максимальное напряжение, предшествующее разрушению материала. Это максимальное напряжение σB называют временным сопротивлением или пределом прочности. σT и σВ характеризуют прочность материала. Чем они больше, тем прочнее материал.
Участок CD соответствует появлению и развитию на образце локального сужения (шейки). Фактическое напряжение здесь продолжает увеличиваться за счёт уменьшения площади поперечного сечения образца, но регистрируемое напряжение s = F / S0уменьшается. Точка D соответствует разрыву образца.
Площадь под кривой растяжения пропорциональна работе разрушения материала. Чем больше эта площадь, тем больше работа разрушения и соответственно выше вязкость материала
Величину называют относительным удлинением, а величину – относительным сужением.
Обе эти величины характеризуют пластичность материала. Чем они больше, тем пластичней материал. Если , а , то материал считается надёжным.
Источник