Испытание материалов на растяжение для
Лабораторная работа № 1
Цель работы – изучить поведение малоуглеродистой стали при растяжении и определить ее механические характеристики.
Основные сведения
Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.
Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.
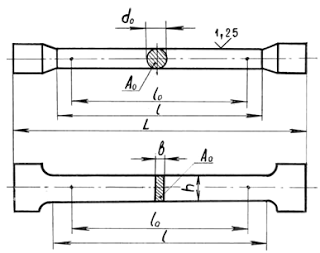
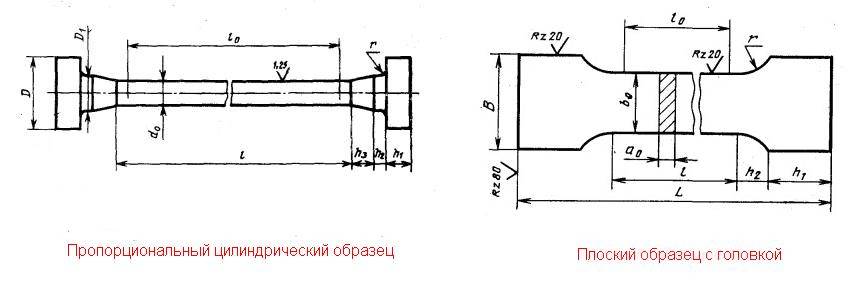
В таких случаях, кроме металлографических исследований, определяются главные механические характеристики на образцах, взятых из зоны разрушения конструкции. Образцы изготавливаются по ГОСТ 1497-84 и могут иметь различные размеры и форму (рис. 1.1).
Рис. 1.1. Образцы для испытания на растяжение
Между расчетной длиной образца lо и размерами поперечного сечения Ао (или dо для круглых образцов) выдерживается определенное соотношение:
В испытательных машинах усилие создается либо вручную — механическим приводом, либо гидравлическим приводом, что присуще машинам с большей мощностью.
В данной работе используется универсальная испытательная машина УММ-20 с гидравлическим приводом и максимальным усилием 200 кН, либо учебная универсальная испытательная машина МИ-40КУ (усилие до 40 кН).
Порядок выполнения и обработка результатов
Образец, устанавливаемый в захватах машины, после включения насоса, создающего давление в рабочем цилиндре, будет испытывать деформацию растяжения. В измерительном блоке машины есть шкала с рабочей стрелкой, по которой мы наблюдаем рост передаваемого усилия F.
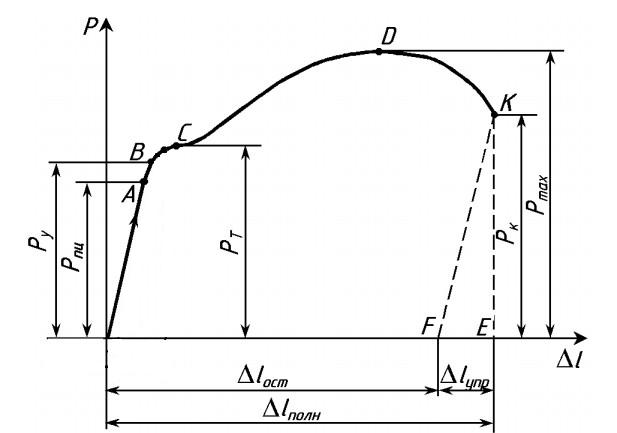
Зависимость удлинения рабочей части образца от действия растягивающей силы во время испытания отображается на миллиметровке диаграммного аппарата в осях F-Δl (рис. 1.2).
В начале нагружения деформации линейно зависят от сил, потому участок I диаграммы называют участком пропорциональности. После точки В начинается так называемый участок текучести II.
На этой стадии стрелка силоизмерителя как бы спотыкается, приостанавливается, от точки В на диаграмме вычерчивается либо прямая, параллельная горизонтальной оси, либо слегка извилистая линия — деформации растут без увеличения нагрузки. Происходит перестройка структуры материала, устраняются нерегулярности в атомных решетках.
Далее самописец рисует участок самоупрочнения III. При дальнейшем увеличении нагрузки в образце происходят необратимые, большие деформации, в основном концентрирующиеся в зоне с макронарушениями в структуре – там образуется местное сужение — «шейка».
На участке IV фиксируется максимальная нагрузка, затем идет снижение усилия, ибо в зоне «шейки» сечение резко уменьшается, образец разрывается.
При нагружении на участке I в образце возникают только упругие деформации, при дальнейшем нагружении появляются и пластические — остаточные деформации.
Если в стадии самоупрочнения начать разгружать образец (например, от т. С), то самописец будет вычерчивать прямую СО1. На диаграмме фиксируются как упругие деформации Δlу (О1О2), так и остаточные Δlост (ОО1). Теперь образец будет обладать иными характеристиками.
Так, при новом нагружении этого образца будет вычерчиваться диаграмма О1CDЕ, и практически это будет уже другой материал. Эту операцию, называемую наклеп, широко используют, например, в арматурных цехах для улучшения свойств проволоки или арматурных стержней.
Диаграмма растяжения (рис. 1.2) характеризует поведение конкретного образца, но отнюдь не обобщенные свойства материала. Для получения характеристик материала строится условная диаграмма напряжений, на которой откладываются относительные величины – напряжения σ=F/A0 и относительные деформации ε=Δl/l0 (рис. 1.3), где А0, l0 – начальные параметры образца.
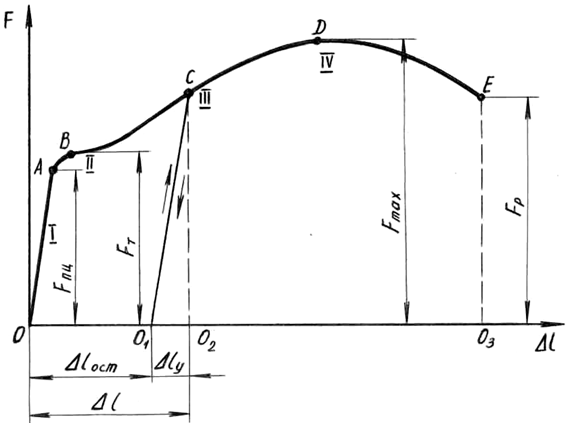
Рис. 1.2. Диаграмма растяжения образца из малоуглеродистой стали
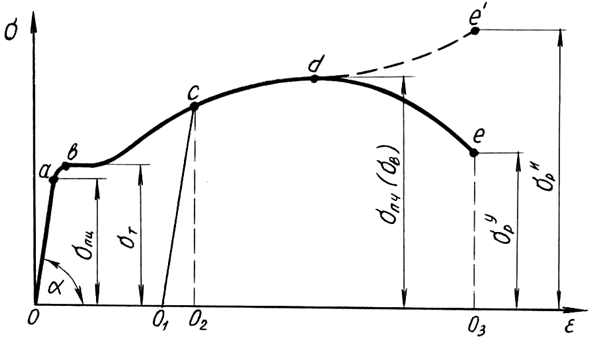
Рис. 1.3. Условная диаграмма напряжений при растяжении
Условная диаграмма напряжений при растяжении позволяет определить следующие характеристики материала (рис. 1.3):
σпц – предел пропорциональности – напряжение, превышение которого приводит к отклонению от закона Гука. После наклепа σпц может быть увеличен на 50-80%;
σу – предел упругости – напряжение, при котором остаточное удлинение достигает 0,05%. Напряжение σу очень близко к σпц и обнаруживается при более тонких испытаниях. В данной работе σу не устанавливается;
σт – предел текучести – напряжение, при котором происходит рост деформаций при постоянной нагрузке.
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют ≈0,2% (рис. 1.4);
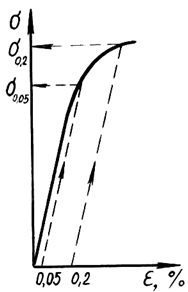
Рис. 1.4. Определение предела упругости и условного предела текучести
σпч (σв) – предел прочности (временное сопротивление) – напряжение, соответствующее максимальной нагрузке;
σр – напряжение разрыва. Определяется условное σур и истинное σир=Fр/Аш, где Аш – площадь сечения «шейки» в месте разрыва.
Определяются также характеристики пластичности – относительное остаточное удлинение
δ = (l1 – l0)∙100% / l0,
где l1 – расчетная длина образца после разрыва,
и относительное остаточное сужение
ψ = (А0 — Аш)∙100% / А0.
По диаграмме напряжений можно приближенно определить модуль упругости I рода
E=σпц/ε=tgα,
причем после операции наклепа σпц возрастает на 20-30%.
Работа, затраченная на разрушение образца W, графически изображается на рис. 1.2 площадью диаграммы OABDEO3. Приближенно эту площадь определяют по формуле:
W = 0,8∙Fmax∙Δlmax.
Удельная работа, затраченная на разрушение образца, говорит о мере сопротивляемости материала разрушению w = W/V, где V = A0∙l0 – объем рабочей части образца.
По полученным прочностным и деформационным характеристикам и справочным таблицам делается вывод по испытуемому материалу о соответствующей марке стали
Контрольные вопросы
- Изобразите диаграмму растяжения образца из малоуглеродистой стали (Ст.3). Покажите полные, упругие и остаточные абсолютные деформации при нагружении силой, большей, чем Fт.
- На каком участке образца происходят основные деформации удлинения? Как это наблюдается на образце? Какие нагрузки фиксируются в этот момент?
- Объясните, почему после образования шейки дальнейшее растяжение происходит при все уменьшающейся нагрузке?
- Перечислите механические характеристики, определяемые в результате испытаний материала на растяжение. Укажите характеристики прочности и пластичности.
- Дайте определение предела пропорциональности.
- Дайте определение предела упругости.
- Дайте определение предела текучести.
- Дайте определение предела прочности.
- Как определить предел текучести при отсутствии площадки текучести? Покажите, как это сделать, по конкретной диаграмме.
- Какие деформации называются упругими, какие остаточными? Укажите их на полученной в лабораторной работе диаграмме растяжения стали.
- Как определяется остаточная деформация после разрушения образца?
- Выделите на диаграмме растяжения образца из мягкой стали упругую часть его полного удлинения для момента действия максимальной силы.
- Какое явление называется наклепом? До какого предела можно довести предел пропорциональности материалов с помощью наклепа?
- Как определяется работа, затраченная на разрушение образца? О каком свойстве материала можно судить по удельной работе, затраченной на разрушение образца?
- Как определить марку стали и допускаемые напряжения для нее после проведения лабораторных испытаний?
- Чем отличается диаграмма истинных напряжений при растяжении от условной диаграммы?
- Можно ли определить модуль упругости материала по диаграмме напряжений?
- Как определить работу, затрачиваемую на деформации текучести лабораторного образца?
Испытание материалов на сжатие >
Краткая теория >
Примеры решения задач >
Источник
Испытание на растяжение металла заключаются в растяжении образца с построением графика зависимости удлинения образца (Δl) от прилагаемой нагрузки (P), с последующим перестроением этой диаграммы в диаграмму условных напряжений (σ — ε)
Испытания на растяжение проводятся по ГОСТ 1497, по этому же ГОСТу определяются и образцы на которых проводятся испытания.
Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
- Участок ОА — участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
- Участок ОВ — участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении
Выше точки В диаграмма растяжения отходит от прямой — деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.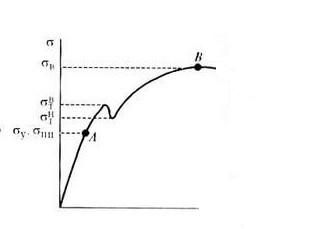
Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение — шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.
Прилагаемая нагрузка для растяжения образца зависит от геометрии этого образца. Чем больше площадь сечения, тем более высокая нагрузка необходима для растяжения образца. По этой причине, получаемая машинная диаграмма не дает качественной оценки механических свойств материала. Чтобы исключить влияние геометрии образца, машинную диаграмму перестраивают в координатах σ − ε путем деления ординат P на первоначальную площадь сечения образца A0 и абсцисс ∆l на lо. Перестроенная таким образом диаграмма называется диаграммой условных напряжений. Уже по этой, новой диаграмме, определяют механические характеристики материала.
Определяются следующие механические характеристики:
Предел пропорциональности σпц – наибольшее напряжение, после которого нарушается справедливость закона Гука σ = Еε , где Е – модуль продольной упругости, или модуль упругости первого рода. При этом Е =σ/ε = tgα , т. е. модуль E это тангенс угла наклона прямолинейной части диаграммы к оси абсцисс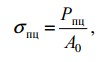
Предел упругости σу — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σу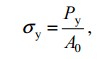
Предел текучести σт – напряжение, при котором происходит увеличение деформации без заметного увеличения растягивающей нагрузки
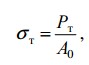Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести
Предел прочности (временное сопротивление разрыву) σв – напряжение, соответствующее наибольшей нагрузке Pmax , предшествующей разрыву образца
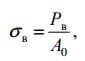
Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности — относительное удлинение δ и относительное сужение ψ
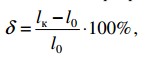
где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца
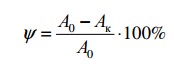
Источник
Механические характеристики материала определяются в результате испытания образца на специальных прессах. Форма образца может быть различной, но чаще всего стержень с участком постоянного поперечного сечения (круглого или прямоугольного) длиной . Концы образца имеют специальные утолщения для их закрепления в испытательной машине.
Перед началом испытания материала на растяжение замеряется площадь поперечного сечения () средней части образца. Значение растягивающей силы (P) и удлинения его средней части () в каждый момент нагружения определяются специальными устройствами. При испытании нагрузка увеличивается медленно и плавно.
Современные испытательные машины снабжены записывающим прибором, который при испытании образца автоматически вычерчивает график зависимости между нагрузкой (P) и абсолютным удлинением (). График называется диаграммой растяжения (или диаграмма Бернулли).
Рассмотрим диаграмму растяжения для стали марки Ст. 3 (рис. 2.3). Эта диаграмма характеризует поведение данного образца, но не материала, из которого он сделан.
В начальной стадии испытания, до точки А с ординатой , зависимость между силой (P) и удлинением () носит линейный характер, что свидетельствует о линейной деформируемости образца. Затем диаграмма искривляется и при некотором значении растягивающей силы наблюдается значительный рост удлинения образца без увеличения нагрузки (текучесть материала). Практически горизонтальный участок диаграммы BC называется площадкой текучести, а точка B – критической точкой диаграммы.
При некотором значении растягивающей силы , соответствующем критической точке B (см. рис. 2.3), на поверхности образца, если он, например, полирован, заметно появление сначала нескольких полосок, параллельных между собой и расположенных под углом примерно к оси образца. Далее появляется вторая система линий, пересекающая первую и наклоненную к оси под тем же углом, что и первая. Такая система сопряженных линий называется линиями Людерса – Чернова, представляющие собой следы сдвигов частиц материала. Направления линий Людерса-Чернова соответствует площадкам, на которых при растяжении возникают наибольшие касательные напряжения.
За точкой C диаграммы удлинение образца начинает расти быстрее нагрузки. Число линий Людерса – Чернова растет, они сливаются друг с другом и, наконец, теряют ясность своих очертаний. Этот участок диаграммы растяжения называется зоной упрочнения.
В наивысшей точке диаграммы D при силе равной на образце внезапно появляется местное сужение – шейка, которая представляет собой результат накопления деформаций сдвига.
Сопротивление образца растяжению, после образования шейки, падает и его разрыв происходит в точке K при нагрузке:
.
При разрыве образца, как правило, появляется поперечная трещина в центре тяжести поперечного сечения (посредине шейки), а остальная часть сечения скалывается под углом к оси образца так, что на одной части разорванного образца образуется выступ, а на другой – кратер.
Линия разгрузки образца KL оказывается прямой и параллельной начальному участку диаграммы ОА. Следовательно, полная деформация образца состоит из двух частей: упругой, исчезающей после снятия нагрузки, и остаточной (пластической).
Источник
Цель работы: определение характеристик механических свойств углеродистой стали при испытании на растяжение.
Конструкционные материалы – это твердые материалы, предназначенные для изготовления изделий, подвергаемых механической нагрузке.
Конструкционные материалы можно разбить на следующие типы:
1. Металлы и сплавы (стали, чугуны, цветные металлы и т. д.).
2. Неметаллические материалы (полимеры, пластмассы, древесные материалы, резины и т. д.).
3. Композиционные материалы. Это материалы, объединенные разными способами в монолит и сохраняющие при этом индивидуальные особенности.
Компоненты композиционного материала различны по геометрическому признаку. Компонент, который обладает непрерывностью по всему объему, называется матрицей (связующим). Матрицы могут быть полимерными, металлическими и т. д. Компонент же прерывный, разделенный в объеме композиционного материала, считается армирующим или упрочняющим. Эти компоненты, как правило, обладают высокой прочностью, твердостью и по этим показателям значительно превосходят матрицу. Прообразом современных композиционных материалов считается железобетон.
Несмотря на достигнутые успехи в создании и использовании неметаллических материалов (пластмассы, полимеры и др.), основными конструкционными материалами еще долгое время будут оставаться металлы и сплавы. Поэтому только они и рассматриваются в данном курсе (из-за ограниченного объема часов).
Под металлами понимают вещества, обладающие металлическим блеском, высокими пластичностью, тепло- и электропроводностью, прочностью. К металлам относятся не только чистые металлы, но и сплавы.
В качестве конструкционных материалов в основном используются сплавы, так как они обладают более высокими механическими свойствами по сравнению с чистыми металлами.
Для конструкционных материалов особенно важны механические свойства, так как они характеризуют возможность их использования в изделиях, эксплуатируемых при воздействии механических нагрузок. Количественные характеристики механических нагрузок определяют в результате испытаний.
К числу наиболее распространенных статических испытаний, позволяющих определить основные характеристики механических свойств металла, относятся испытания на растяжение, которые рассмотрены в лабораторной работе № 8.
Многие электротехнические материалы в установках одновременно с электрической несут и механическую нагрузку (например, провода ЛЭП, троллейбусов, трамваев и т. д.). Поэтому для них наряду с электрическими параметрами необходимо знать и механические (предел прочности sв и относительное остаточное удлинение d). Эти параметры очень важны при правильном выборе материала, т. к. у одного и того же материала в зависимости от технологии изготовления эти параметры могут изменяться в широких пределах. В ряде случаев приходится за счет ухудшения электрических параметров увеличивать механическую прочность. Например, в контактных проводах троллейбусов и трамваев благодаря высокой прочности бронза стала применяться вместо меди.
Для сравнения в таблице 8.1 приведены механические свойства некоторых проводников [2].
Таблица 8.1
| Материал | Предел прочности sв, МПа | Относительное удлинение d,% |
| Алюминий мягкий (АМ) | 10−18 | |
| Алюминий твердый (АТ) | 160−170 | 1,5−2 |
| Медь мягкая (ММ) | 260−280 | 18−35 |
| Медь твердая (МТ) | 360−390 | 0,5−2,5 |
| Бронза | 800−1200 | 1,5−10 |
Для определения механических характеристик прочности и пластичности проводят испытания на растяжение образцов из исследуемого материала в испытательных машинах. В лабораторной работе испытываются образцы из углеродистой конструкционной стали, которая и в энергетике нашла широкое применение (из нее делают опоры линий электропередач, порталы и осветительные вышки на подстанциях и т. д.).
Углерод в сталь вводится специально, т. к. с повышением его содержания существенно возрастает прочность стали.
Углеродистые стали относятся к числу самых распространённых конструкционных материалов [5]. Объём их производства достигает 85 % от общей выплавки стали. Достоинствами углеродистых сталей являются удовлетворительные механические свойства в сочетании с технологичностью обработки и низкой стоимостью.
Углеродистые стали подразделяются на три основные группы [5]:
− обыкновенного качества;
− качественные стали (общего назначения);
− стали специального назначения (котельную, мостовую, судостроительную и др.).
Углеродистые стали обыкновенного качества характеризуются значительным содержанием вредных примесей, неметаллических включений, газов. Они обозначаются буквами «Ст» и цифрами от 0 до 6. В зависимости от назначения и гарантируемых свойств их подразделяют на три группы: А, Б, В. Эти стали применяются для изготовления металлоконструкций, ненагруженных деталей машин и механизмов, крепёжных деталей, рельсов и т. д.
Углеродистые качественные стали имеют меньшее по сравнению со сталями обыкновенного качества содержание вредных примесей и неметаллических включений. Поставляют их в виде проката, поковок, профилей различного назначения с гарантированными механическими свойствами и химическим составом. Эти стали маркируют двухзначными цифрами от 05 до 85, обозначающими среднее содержание углерода в сотых долях процента. Например, сталь Ст20 содержит в среднем 0,20 % углерода. Эти стали применяют в машиностроении и приборостроении для изготовления кузовов автомобилей, корпусов, зубчатых колёс, осей и т. д.
Углеродистые стали специального назначения отличаются хорошей обрабатываемостью, они предназначены в основном для приготовления деталей массового производства. При обработке, например, автоматных сталей на станках-автоматах образуется короткая и мелкая стружка. Котельнаясталь хорошо сваривается. Из неё изготавливают котлы, судовые топки, камеры горения газовых турбин и т. д.
Испытание на растяжение относится к числу наиболее распространенных статических испытаний, позволяющих определить основные характеристики механических свойств металла. К преимуществам такого испытания относятся: сравнительная простота эксперимента и возможность получить растяжение в чистом виде.
Для испытания используются стандартные образцы с рабочей частью в виде цилиндра (цилиндрические образцы) или стержни с прямоугольным сечением (плоские образцы). Размеры образцов устанавливает ГОСТ 1497-84.
На рисунке 8.1 показан цилиндрический образец для испытания (до и после испытаний). На рисунке 8.2 показано изображение образца на экране монитора.
Рис. 8.1 Образец до и после испытаний
Отношение начальной расчетной длины рабочей части образца к начальному диаметру do, т. е. k = , называют кратностью образца. Применяются образцы с кратностью 2, 5 и 10. Самым распространенным является образец с кратностью k = 5 (такой образец испытывается в лабораторной работе).
Рис. 8.2. Цилиндрический образец для испытания на растяжение: − начальная длина
рабочей части; do−начальный диаметр; L – полная длина образца
На рисунке 8.3 приведена фотография испытательной машины ZDM-10, а на рисунке 8.4 – изображение испытательной машины на экране ЭВМ.
Рис. 8.3. Испытательная машина ZDM-10
Рис. 8.4. Изображение испытательной машины на экране монитора
Перед испытанием образец закрепляют в вертикальном положении. В процессе испытания диаграммный механизм машины непрерывно регистрирует так называемую первичную (машинную) диаграмму растяжения в координатах: нагрузка Р – абсолютное удлинение образца Dℓ (рис. 8.5). У образца удлинение небольшое (всего 6−10 мм), поэтому для наглядности на диаграмме удлинение откладывается в масштабе (в лабораторной работе масштаб = 100/6). На экране монитора удлинение без масштаба обозначено dℓ, так как на клавиатуре нет знака ,а в масштабе – dℓm.
Рис. 8.5. Машинная (первичная) диаграмма растяжения
пластичного материала с площадкой текучести
Начальный криволинейный участок диаграммы не учитывают, так как он образуется за счет выборки зазоров в узлах машины и местного обмятия головок образца в захватах, т. е. не характеризует свойств испытуемого материала. За начало координат диаграммы принимают точку пересечения оси абсцисс с прямой, проходящей через начальный участок диаграммы.
На диаграмме растяжения материалов можно выделить несколько характерных участков (рис. 8.5). Прямолинейный участок ОА соответствует упругой деформации образца. Дальнейшее возрастание нагрузки (участок АВ) приводит к появлению пластической (остаточной) деформации. Причем у некоторых материалов наблюдается интенсивная пластическая деформация при неизменной нагрузке (участок BB′). Такой участок диаграммы называется площадкой текучести. Однако многие металлы и сплавы деформируются при растяжении без площадки текучести (см. рис. 8.8).
До максимальной нагрузки (рис. 8.5, точка C) происходит равномерная деформация образца по всей его рабочей части. А затем образец в наиболее слабом месте утончается (это место называется шейкой), и на участке СD идет пластическая деформация при снижении нагрузки. В точке D происходит окончательное разрушение образца с разделением его на две части.
По диаграмме растяжения определяют характеристики механических свойств металла. Причем в качестве характеристики прочности принимают не нагрузку Р, а условное напряжение s, определяемое отношением нагрузки к площади начального поперечного сечения образца Fо
.
По оси абсцисс откладывается относительное удлинение = Dℓ/ℓo(в о. е.) или = Dℓ/ℓo∙100 %. (Так как на клавиатуре нет буквы , то она заменена на букву E).
На рисунке 8.6 приведены диаграммы условного и истинного напряжений.
Диаграмма напряжений называется условной (приближенной), потому что напряжения найдены по начальной площади поперечного сечения образца Fо, и не учитывает уменьшения сечения (рис. 8.6а). Если в процессе испытания постоянно измерять диаметр образца и вычислять истиное напряжение с учетом сужения, то на этой диаграмме (рис. 8.6б) напряжение возрастает вплоть до разрыва образца.
В лабораторной работе рассматривается условная диаграмма напряжений (рис. 8.7). По этой диаграмме определяются основные характеристики прочности и пластичности.
Рис. 8.6. Диаграммы напряжений: а) условная; б) истинная
Прочность – это свойство материала сопротивляться деформации или разрушению. Рассмотрим основные характеристики прочности.
В области упругой деформации (участок ОА, рис. 8.5) зависимость между напряжением s и относительной деформацией пропорциональна и известна под названием закона Гука:
s = Е· ,
где Е – модуль Юнга или модуль нормальной упругости измеряется в МПа и характеризует жесткость материала. Чем выше Е, тем материал жестче, т. е. меньшую упругую деформацию вызывает одна и та же нагрузка.
Предел пропорциональности(sпц) − это напряжение, при котором отступление от линейной зависимости достигает некоторого значения, установленного техническими условиями. В качестве технического условия обычно берут следующее: при напряжении sпц тангенс угла наклона, образованного касательной к кривой деформации с осью нагрузок, увеличивается на 50 % по сравнению с линейным участком (более подробно определение основных показателей прочности и пластичности изложено в самой лабораторной работе).
Предел текучести (sт) – это напряжение, при котором материал деформируется (течет) без заметного изменения нагрузки (рис. 8.7).
У большинства материалов диаграмма растяжения не имеет площадки текучести. В этом случае задаются допуском на остаточную деформацию образца и определяют условный предел текучести.
Рис. 8.7. Определение основных характеристик прочности
Условный предел текучести (s0.2) – это напряжение, при котором остаточное удлинение достигает 0,2 % от начальной расчетной длины образца
(рис. 8.9). Здесь отрезок OA равен 0,2 % от ℓo.
Рис. 8.8. Определение условного предела текучести s0.2
Предел прочности (временное сопротивление, sв)– это напряжение, соответствующее наибольшей нагрузке (рис. 8.7).
Напряжение при разрыве (σк)–это напряжение,соответствующее моменту разрушения образца (рис. 8.7).
Показатели пластичности.Пластичностью называют свойство материалов необратимо изменять свою форму и размеры под действием внешней нагрузки.
Выше уже была рассмотрена абсолютная (Dℓ) и относительная (ε) деформация под действием нагрузки. Если к материалу приложена небольшая нагрузка (s < σ пц), то возникает только упругая деформация, и после снятия нагрузки образец восстанавливает свою первоначальную длину . А если напряжение s > σ пц, то после снятия нагрузки разгрузка образца идет по прямой, параллельной упругой деформации OA (например, по прямой DF, рисунок 8.5). Отрезок OF соответствует остаточной деформации D образца. Относительное остаточное удлинение в этом случае определяется как
d = .
Источник