Интегралы задача на растяжение
Алгебра и начала математического анализа, 11 класс
Урок №25. Применение интегралов для решения геометрических и физических задач.
Перечень вопросов, рассматриваемых в теме
1) Знакомство с применением определенного интеграла в различных предметных областях
2) Знакомство с прикладными задачами, связанными с вычислением определенного интеграла в физике, экономике, геометрии.
3) Решение задач, с помощью определенных интегралов
путь, пройденный телом
Прирост численности популяции N(t) за промежуток времени от t0 до T равен 
.
Объем тела вращения 
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием этой криволинейной трапеции
формула Ньютона – Лейбница
путь, пройденный телом
Прирост численности популяции N(t) за промежуток времени от t0 до T равен 
.
Объем тела вращения 
Примеры и разбор решения заданий тренировочного модуля
№1 Найти объем тела вращения вокруг оси 0х , ограниченной прямыми у=0, х=0ю у= х2, х=4.
Решение: Построим тело вращения, образованного вращением фигуры вокруг оси 0х
Воспользуемся формулой Ньютона-Лейбница.
и формулой нахождения объемов тел вращения. 
Далее подставляем значения в формулу и рассчитываем объем тела вращения.
Ответ 51,2 ед3
№2. Сила в 1 Н растягивает пружину на 3 см. Какую работу она при этом производит?
Решение.
Если F–сила, А – работа S– перемещение, то F = A’(S).
Обратимся к физике.
По закону Гука сила пропорциональна растяжению или сжатию пружины, т. е. F = kx, где k – коэффициент пропорциональности, х – величина растяжения или сжатия.
Используя данные задачи, найдите коэффициент k. Подставим данные в задаче величины в уравнение, выражающее закон Гука. Получим: 
.
Следовательно, сила, растягивающая нашу пружину, выразится следующим образом:
.
Так как сила начинает действовать на пружину в состоянии покоя, то работа 
Ответ: 0,015 Дж
№3. Аквариум имеет форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды 1000 кг/м3), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4 м x 0,7 м.
Решение.
Выберем систему координат так, чтобы оси Оy и Оx соответственно содержали верхнее основание и боковую сторону вертикальной стенки аквариума. Для нахождения силы давления воды на стенку воспользуемся формулой
Р=
Стенка имеет форму прямоугольника, поэтому f(x)=0.7x, xϵ [0;0.4] Так как пределы интегрирования а=0 и b=0,4, то получим:
Ответ: 549 Н
№4 Скорость прямолинейного движения тела выражается формулой 
. Найти путь, пройденный телом за 5 секунд от начала движения.
Решение.
Физический смысл производной: если тело движется по закону S = S(t), то скорость тела в момент времени t0 равна значению производной функции S(t) в этой точке, т. е. v = S’(t0). Тогда обратное утверждение: если скорость движения тела задана уравнением v = v(t), то путь, пройденный телом от момента времени t = a до момента времени t = b равен 
. Подставим уравнение скорости в формулу и рассчитаем путь.
Ответ 150м
Источник
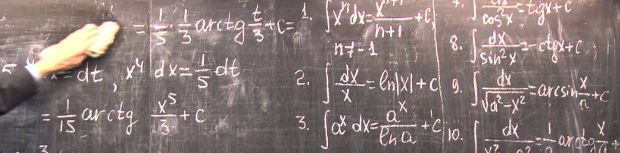
| Срок выполнения | от 1 дня |
| Цена | от 50 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
УЗНАТЬ СТОИМОСТЬ РЕШЕНИЯ ИНТЕГРАЛОВ
Интеграл: что это?
Интеграл является одним из важнейших понятий математики. Понятие «интеграл» возникло в связи со следующими потребностями:
- отыскание функции по ее производной (например, нахождение функции пути по известной функции скорости);
- измерение различных характеристик объектов (например, площади плоской фигуры и т.д.).
Различают несколько видов интегралов: неопределенный, определенный и несобственный интегралы.
Интеграл: как вычислить?
Для вычисления большинства интегралов достаточно помнить таблицу интегралов, а также знать основные правила интегрирования. Основная часть таблицы, которая используется наиболее часто, содержит порядка 15 формул, правил интегрирования тоже не так много. Но если уж совсем плохо запоминается, то найти таблицу и правила можно в любом учебнике, в котором рассматривается данная тема.
Вычисление интеграла состоит из нескольких этапов:
- приведение подынтегральной функции к сумме табличных функций;
- разложение интеграла на сумму табличных интегралов;
- вычисление каждого интеграла по отдельности;
- формирование окончательного решения.
Это только поначалу кажется сложным, однако при наличии некоторого опыта по вычислению интегралов каждая пара этапов (1 и 2; 3 и 4) интуитивно объединяются в один этап.
При вычислении определенных интегралов основной является формула Ньютона-Лейбница, которую обязательно (!) нужно запомнить:
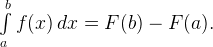
Между производной и неопределенным интегралом существует взаимосвязь, которую можно выразить следующими равенствами:
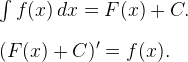
Следовательно, при умении находить производную функции всегда можно проверить правильность вычисления интеграла.
Приложение интеграла к решению задач
Область применения интегралов достаточно широка. Очень часто интегралы используются при решении задач по геометрии, биологии, механике, экономике и т.д.
В зависимости от того, какая задача решается, требуется вычислить либо определенный, либо неопределенный интеграл.
Самая простейшая задача на интегралы формулируется следующим образом: вычислить неопределенный (определенный) интеграл.
Пример. Вычислить определенный интеграл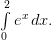 
Как правило, решение задач с интегралами выполняется с использованием некоторой формулы, будь то формула вычисления площади плоской фигуры, длины дуги или какая-то другая формула. Поэтому решение любой задачи с интегралами можно выполнить в три этапа:
- выбор формулы;
- определение пределов интегрирования (если используется определенный интеграл);
- непосредственное вычисление интеграла.
Приложение интеграла к решению задач в геометрии
Основными формулами при решении задач с интегралами по геометрии являются:
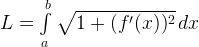— длина дуги
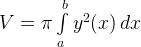— объем тела вращения
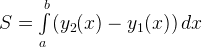— площадь плоской фигуры
Пример. Вычислить объем тела вращения, образованного вращением кривой y = x2 вокруг оси ОХ, x ∈ [0, 2].
Решение. На первом этапе определяется используемая для решения задачи формула. В рассматриваемой задаче все сказано в условии «вычислить объем тела вращения». Следовательно, используем формулу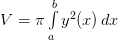 
.
Переходим ко второму этапу решения задачи. Пределы интегрирования также заданы условием задачи (x ∈ [0, 2]), следовательно, остается только подставить все необходимое в формулу.
На третьем этапе необходимо вычислить полученный интеграл, который, кстати, является табличным интегралом.
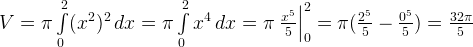
Приложение интеграла к решению задач в механике
Основными формулами при решении задач с интегралами по механике являются:
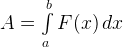— работа переменной силы
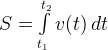— путь, пройденный телом
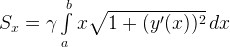— статистический момент
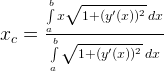— координата х центра тяжести
Пример. Тело движется со скоростью v(t) = t + 2 (м/с). Найти путь, который пройдет тело за 2 секунды после начала движения.
Решение. На первом этапе определяется необходимая для решения задачи формула. Из условия задачи видно, что используется формула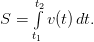 
Пределы интегрирования также заданы условием задачи (t1 = 0 — время начала движения; t2 = 2 — время завершения движения), следовательно, остается только подставить все необходимое в формулу и вычислить полученный интеграл.
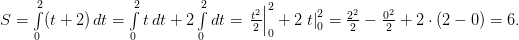
Примечание: при вычислении интеграл был приведен к сумме табличных интегралов.
Пример. Тело движется с ускорением 2 м/с2. Найти в общем виде функции, задающие изменение скорости и пройденный путь.
Решение. На первом этапе определяется используемая для решения задачи формула. Взаимосвязь между ускорением и скоростью аналогична взаимосвязи между скоростью и путем. Для определения зависимости пути от времени используется формула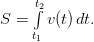 
Для определения же зависимости скорости от времени формула 
.
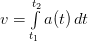В рассматриваемой задаче нет дополнительных условий, поэтому применяется неопределенный интеграл и пределы интегрирования не нужны.
Следовательно, решение задачи сводится к последовательному вычислению двух неопределенных интегралов:
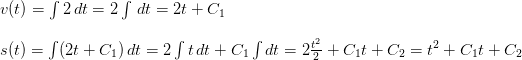
Заключение
Как правило, задачи с интегралами в школьном курсе математики и даже в университете имеют вполне стандартную формулировку, а их решение сводится к выбору формулы, определению пределов интегрирования и вычислению составленного интеграла.
Учите теорию и решайте задачи! И помните, что мы всегда готовы помочь Вам.
Источник
Определённый интеграл применяется при решении задач на вычисление: работы переменной силы; работы, затраченной на растяжке или сжатие пружины; пути, пройденного телом за промежуток времени; давления жидкости на вертикальную поверхность.
Путь, пройденный телом при равномерном движении со скоростью v=f(t) за промежуток времени [t₁;t₂], вычисляется по формуле
S= .
Согласно закону Гука сила F(x), растягивающая (сжимающая) пружину на x m, пропорциональна этому растяжению (сжатию), т.е. F(x)=kx, где
k— коэффициент пропорциональности. Работа A, совершаемая переменной силой F(x) на отрезке [a;b], вычисляется по формуле
A=
Сила давления p жидкости на вертикальную пластинку, погружённую в жидкость, вычисляется по формуле
p=pg
где g=9,81 м/с²- ускорение свободного падения;
p— плотность жидкости кг/м³;
a,b – изменение глубины погружения пластинки, м.
Вычислить следующие определенные интегралы:
1)
Решение. Находим
2)
Решение. Имеем
3)
Решение. Имеем
4)
Решение. Имеем
5)
Решение: Имеем
6)
Решение: Имеем
7)
Решение: Имеем
8)
Решение: Введем новую переменную интегрирования с помощью подста-
новки
2х — 1= и. Дифференцируя, имеем 2dx=dи, откуда dx=(1/2) du. Находим-
новые пределы интегрирования. Подставляя в соотношение 2х-1=и
значения х=2 и х=3, соответственно получим =2*2 — 1=3, =2*3 — 1=5.
Следовательно,
9)
Решение: Положим 5х — 1=и; тогда 5dx=du, dx=(1/5)du. Вычисляем новые пределы интегрирования: =5*1 — 1=4, =5*2 — 1=9. Следовательно,
10)
Решение: Положим 2 +1 = и; тогда . Вычисляем новые пределы интегрирования: . Таким образом,
11)
Решение: Преобразуем подкоренное выражение: . Поло-
жим Зх/2=и, откуда dх=(2/3)du. Найдем новые пределы-интегрирования:
. Таким образом:
12)
Решение:
Положим u=ln х, dv=x dx; тогда . Следовательно,
.
Пример: Вычислить площадь фигуры, ограниченной указанными линиями:
x+2у-4=0, у=0, х=-3 и х=2.
Решение:
Выполним построение фигуры. Строим прямую х+2у-4=0 по двум точкам А(4;0) и В(0;2).
Выразив у через х, получим у=- 0,5х+2.
По формуле (1), где ƒ(х)= — 0,5х+2, а=-3, b=2, находим
S= =11,25 (кв.ед.)
В качестве проверки вычислим площадь трапеции М₁ МNN₁ обычным путем. Находим: M₁ M=ƒ(-3)= — 0,5(-3)+2=3,5, N₁ N=ƒ(2)= — 0,5∙2+2=1, М₁ N₁=5. Следовательно, S=0,5(3,5+1)∙5=11,25 (кв.ед.).
Пример: Вычислить площадь фигуры, ограниченной указанными линиями:
у= и у=2х.
Решение: Данная фигура ограничена параболой у = и прямой у = 2х.
Для определения точек пересечения заданных линий решим систему уравнений
откуда находим -2х=0 Используя для нахождения искомой площади формулу (5), получим
S= = (кв.ед.).
Пример: Скорость движения точки изменяется по закону υ=(3t²+2t+1) . Найти путь, пройденный точкой за 10 с от начала движения.
Решение:
Согласно условию, ƒ(t)= 3t²+2t+1, t₁=0, t₂=10. По формуле (6) находим
S= 3t²+2t+1)dt= =10³+10²+10=1110 (м).
Пример: Тело брошено с поверхности земли вертикально вверх со скоростью
υ =(39,2-9,8t) . Найти наибольшую высоту подъема тела.
Решение:
Тело достигнет наибольшей высоты подъема в такой момент времени t, когда υ=0, т. е. 39,2-9,8t=0, откуда t=4 с. По формуле (6) находим
S= 39,2-9,8t)dt= =78,4 (м).
Пример: Сжатие х винтовой пружины пропорционально приложенной силе F. Вычислить работу силы F при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила 10 Н.
Решение:
Так как х=0,01 м при F=10 Н, то, подставляя эти значения в равенство (8), получим 10=k∙0,01, откуда k=1000 . Подставив теперь в это же равенство значение k, находим F=1000 х, т. е. ƒ(х)=1000 х. Искомую работу найдем по формуле (7), полагая a=0, b=0,04:
A= =0,8 (Дж).
Пример: Цилиндрическая цистерна с радиусом основания 0,5 м и высотой 2 м заполнена водой. Вычислить работу, которую необходимо произвести, чтобы выкачать воду из цистерны.
Решение: Выделим на глубине х горизонтальный слой высотой dx. Работа А, которую надо произвести, чтобы поднять слой воды весом P на высоту х, равна Px.
Изменение глубины х на малую величину dx вызовет изменение объема V на величину dV= и изменение веса P на величину dP=9807 ; при этом совершаемая работа А изменится на величину dA=9807 .
Проинтегрировав это равенство при изменении х от 0 до Н, получим
A= =4903 (Дж).
Пример: Треугольная пластинка с основание 0,2 м и высотой 0,4 м погружена вертикально в воду так, что вершина лежит на поверхности воды, а основание параллельно ей. Вычислить силу давления воды на пластинку.
Решение:
Выделим на глубине х горизонтальную полоску шириной dx.
Изменение глубины х на малую величину dx вызовет изменение силы давления Р на малую величину dP. Площадь полоски DEC имеем у:0,2=х:0,4, откуда у=0,5х.
Следовательно,
dP=9,807
Интегрируя dP при изменении х от 0 до 0,4 , получим
P=4903,5 =4903,5 =1634,5∙0,4³
Вопросы для закрепления теоретического материала к практической работе.
1. Формула Ньютона-Лейбница.
2. Геометрический смысл определённого интеграла.
3. По какой формуле находится объём тела вращения?
4. Формулы приближенного вычисления определённого интеграла.
- При решении физических задач какого типа применяются определённый интеграл
1 | 2 | 3 | 4 |
Источник
Решение физических задач с помощью определенного интеграла
ФИО: Юдкало Ирина Васильевна
Место работы: Муниципальное бюджетное общеобразовательное учреждение «Масловопристанская средняя общеобразовательная школа Шебекинского района Белгородской области»
Должность: учитель математики и информатики
Предмет: математика
Класс: 11
Тема и номер урока в теме: «Решение физических задач с помощью определенного интеграла», 7 (из 8) урок в теме.
Базовый учебник: Алгебра и начала анализа. 10-11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А.Г. Мордкович. – 13-е изд., 2012.
Цель урока: познакомить учащихся с применением производной и интеграла в физике.
Формируемые предметные результаты: умение применять интеграл для решения физических задач.
Формируемые метапредметные результаты:
-личностные универсальные учебные действия:
осознавать потребность и готовность к самообразованию
осознавать единство и целостность окружающего мира, возможности его познаваемости и объяснимости на основе достижений науки (физики, математики)
-регулятивные универсальные учебные действия:
умение развивать мотивы и интересы своей познавательной деятельности;
умение осуществлять контроль своей деятельности в процессе достижения результата;
умение определять способы действий в рамках предложенных условий и требований;
-познавательные универсальные учебные действия
умение выделять главное;
умение ориентироваться в своей системе знаний и осознавать необходимость нового знания;
умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач.
Тип урока: интегрированный урок математики и физики.
Формы работы учащихся: парная, групповая, фронтальная
Необходимое техническое оборудование: проектор.
Структура и ход урока
Оргмомент
Постановка проблемы урока. Мотивация и целеполагание
Сегодня на комплексном уроке математики и физики мы рассмотрим возможности применение математического аппарата для решения задач, описывающих различные физические процессы.
Задача
Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью v1=(2t2+4t)м/с, второе – со скоростью v2=(3t+2) м/с. На каком расстоянии друг от друга они окажутся через 10 с?
Проанализируем условие задачи.
Очевидно, перед нами задача на движение. В чем ее особенность? Скорости тел не являются постоянными, они изменяются с течением времени. Как можно решить? {Предлагаются разные версии, например: найти скорости в каждую секунду времени от 1 до 10 с и вычислить путь, пройденный телами.}
Актуализация опорных знаний
Вспомним основные понятия ранее изученной темы «Интеграл»:
Что такое определенный интеграл?
Как вычислить значение определенного интеграла?
Как называется полученная формула?
Перечислить свойства интеграла.
Работапо теме урока
С помощью определенного интеграла можно решать различные задачи физики, механики и др., которые трудно или невозможно решить методами элементарной математики.
Так, понятие определенного интеграла применяется при решении следующих физических задач:
1. Задача о вычислении пути
2. Задача о вычислении работы переменной силы.
3. Вычисление работы при растяжении или сжатии пружины.
4. Задача о силе давления жидкости на вертикальную поверхность и др.
Несмотря на разнообразие этих задач, они объединяются одной и той же схемой рассуждений при их решении. Искомая величина (путь, работа, давление и т. д.) соответствует некоторому промежутку изменения переменной величины, которая является переменной интегрирования. Эту переменную величину обозначают через Х, а промежуток ее изменения – через [а, b].
Отрезок [a, b] разбивают на n равных частей, в каждой из которых можно пренебречь изменением переменной величины. Этого можно добиться при увеличении числа разбиений отрезка. На каждой такой части задачу решают по формулам для постоянных величин.
Далее составляют сумму (интегральную сумму), выражающую приближенное значение искомой величины. Переходя к пределу при n, находят искомую величину I в виде интеграла
I = 
, где f(x) – данная по условиям задачи функция (сила, скорость и т. д.).
Рассмотрим общие схемы решения задач разных видов.
{В зависимости от уровня подготовленности учащихся, можно предложить эту работу по группам}
Задача 1. Нахождение пути, пройденного телом при прямолинейном движении с переменным ускорением.
Как известно, путь, пройденный телом при равномерном движении за время t, вычисляется по формуле S = vt.
Если тело движется неравномерно в одном направлении и скорость его меняется в зависимости от времени t, т. е. v = f(t), то для нахождения пути, пройденного телом за время от t1 до t2, разделим этот промежуток времени на n равных частей Δt. В каждой из таких частей скорость можно считать постоянной и равной значению скорости в конце этого промежутка. Тогда пройденный телом путь будет приблизительно равен сумме 
, т.е.
Если функция v(t) непрерывна, то 
Задача 2. Вычисление работы переменной силы, произведенной при прямолинейном движении тела
Пусть тело под действием силы F движется по прямой s, а направление силы совпадает с направлением движения. Необходимо найти работу, произведенную силой F при перемещении тела из положения a в положение b.
Если сила F постоянна, то работа находится по формуле 
(произведение силы на длину пути).
Пусть на тело, движущееся по прямой Ох, действует сила F, которая изменяется в зависимости от пройденного пути, т. е.
. Для того чтобы найти работу, совершаемую силой F на отрезке пути о а до b, разделим этот отрезок на n равных частей Δx. Предположим, что на каждой части Δx сила сохраняет постоянное значение 
Составим интегральную сумму, которая приближенно равна значению произведенной работы: 
т.е. работа, совершенная этой силой на участке от а до b, приближенно мала сумме: 
Итак, работа переменной силы вычисляется по формуле: 
Задача 3. Вычисление работы, затраченной на растяжение или сжатие пружины
Согласно закону Гука, сила F, необходимая для растяжения или сжатия пружины, пропорциональна величине растяжения или сжатия.
Пусть х – величина растяжения или сжатия пружины. Тогда F=kx, где k – коэффициент пропорциональности, зависящий от свойства пружины.
Работа на участке Δx выразится формулой ΔAFΔx, а вся затраченная работа 
или 
. Если 
то погрешность величины работы стремится к нулю.
Для нахождения истинной величины работы следует перейти к пределу:
Задача 4 Определение силы давления жидкости на вертикально расположенную пластинку
Из физики известно, что сила Р давления жидкости на горизонтально расположенную площадку S, глубина погружения которой равна h, определяется по формуле: 
, где 
– плотность жидкости.
Выведем формулу для вычисления силы давления жидкости на вертикально расположенную пластинку произвольной формы, если ее верхний край погружен на глубину a, а нижний – на глубину b.
Так как различные части вертикальной пластинки находятся на разной глубине, то сила давления жидкости на них неодинаковa. Для вывода формулы нужно разделить пластинку на горизонтальных полос одинаковой высоты 
. Каждую полосу приближенно можно считать прямоугольником.
По закону Паскаля сила давления жидкости на такую полосу равна силе движения жидкости на горизонтально расположенную пластинку той же площади, погруженной на ту же глубину.
Тогда сила давления на полосу, находящуюся на расстоянии х от поверхности, составит 
, где 
– площадь полосы.
Составим интегральную сумму и найдем ее предел, равный силе давления жидкости на всю пластинку:
т.е.
Если верхний край пластинки совпадает с поверхностью жидкости, то а=0 и формула (5) примет вид
Ширина каждой полосы зависит от формы пластинки и является функцией глубины х погружения данной полосы.
Для пластинки постоянной ширины формула (5) упрощается, т.к. эту постоянную можно вынести за знак интеграла:
Разбор задач по теме
{Одна задача решается у доски с комментированием или на отвернутой доске для дальнейшей проверки. Остальные можно использовать для самостоятельной работы в группах}
1) Скорость движения материальной точки задается формулой 
= (4
м/с. Найти путь, пройденный точкой за первые 4 с от начала движения.
Решение:
2) Скорость движения изменяется по закону 
м/с . Найти длину пути, пройденного телом за 3-ю секунду его движения.
Решение:
3) Скорость движения тела задана уравнением с v=(12t-3t2) м/с. Определить путь, пройденный телом от начала движения до остановки.
Решение:
Скорость движение тела равна нулю в момент начала его движения и остановки. Найдем момент остановки тела, для чего приравняем скорость нулю и решим уравнение относительно t; получим 
Следовательно,
4) Тело брошено вертикально вверх со скоростью, которая изменяется по закону 
м/с. Найти наибольшую высоту подъема.
Решение:
Найдем время, в течении которого тело поднималось вверх: 29,4–9,8t=0 (в момент наибольшего подъема скорость равна нулю); t = 3 с. Поэтому
5) Какую работу совершает сила в 10Н при растяжении пружины на 2 см?
Решение:
По закону Гука сила F, растягивающая пружину, пропорциональна растяжению пружины , т.е. F = kx. Используя условие, находим 
(Н/м), т.е. F = 500x. Получаем
6) Сила в 60Н растягивает пружину на 2 см. Первоначальная длина пружины равна 14 см. Какую работу нужно совершить, чтобы растянуть ее до 20 см?
Решение:
Имеем 
(H/м) и, следовательно, F=3000x. Так как пружину требуется растянуть на 0,06 (м), то
7) Определить силу давления воды на стенку шлюза, длина которого 20 м, а высота 5 м (считая шлюз доверху заполненным водой).
Здесь y = f(x) = 20, a = 0, b = 5 м, 
кг/
.
Находим
8) В воду опущена прямоугольная пластинка, расположенная вертикально. Ее горизонтальная сторона равна 1 м, вертикальная 2 м. Верхняя сторона находится на глубине 0,5 м. Определить силу давления воды на пластинку.
Решение:
Здесь y = 1, a = 0,5, b = 2 + 0,5 = 2,5 (м), 
= 1000 кг/
. Следовательно,
9) Скорость прямолинейного движения точки задана уравнением 
. Найти уравнение движения точки.
Решение:
Известно, что скорость прямолинейного движения тела равна производной пути s по времени t, т.е. 
, откуда ds = v dt. Тогда имеем 
Это искомое уравнение.
10) Скорость тела задана уравнением 
. Найти уравнение движения, если за время 
тело прошло путь 
.
Решение:
Имеем ds = v dt = (6
+ 1) dt; тогда
Подставив в найденное уравнение начальные условия s = 60 м, t = 3 c, получим
откуда С = 3.
Искомое уравнение примет вид
11) Тело движется со скоростью 
м/с. Найти закон движения s(t), если в начальный момент тело находилось на расстоянии 5 см от начала отсчета.
Решение:
Так как ds = v dt = (
, то 
Из условия следует, что если t = 0, то s = 5 см = 0,05 м. подставив эти данные в полученное уравнение, имеем 
откуда 0,05 = С.
Тогда искомое уравнение примет вид
12) Вычислить силу давления воды на плотину, имеющую форму трапеции, у которой верхнее основание, совпадающее с поверхностью воды, имеет длину 10 м, нижнее основание 20 м, а высота 3 м.
Решение:
13) Цилиндрический стакан наполнен ртутью. Вычислить силу давления ртути на боковую поверхность стакана, если его высота 0,1 м, а радиус основания 0,04 м. Плотность ртути равна 13600 кг/
.
Решение:
Вычислим площадь круглой полоски
Элементарная сила давления составляет
Следовательно
Самостоятельное решение задач на доске, коллективный разбор решений задач:
Скорость движения тела задана уравнением
. Найти уравнение движения, если в начальный момент времени 
Найти уравнение движения точки, если к моменту начала отсчета она прошла путь
, а его скорость задана уравнением
