Интеграл мора при растяжении
Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.
Получение формулы интеграла Мора
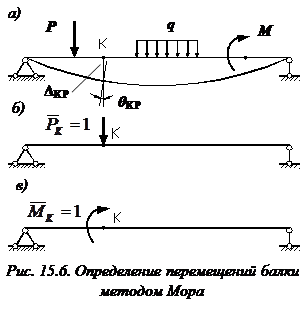
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим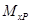 
и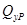 
, соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки (
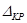) в точке K.
Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой 
(рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.
Внутренние усилия, возникающие во вспомогательной балке, обозначим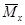 
и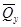 
.
Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда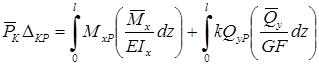 
.
При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).
Тогда, учитывая, что , окончательно получим формулу интеграла Мора: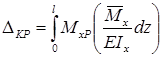 
.
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора, а саму формулу – интегралом Мора.
Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (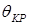
), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент 
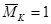(рис. 15.6, в).
порядок вычисления перемещений методом Мора:
· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;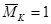
· для каждого участка балки составляем выражения для изгибающих моментов заданной (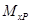) и вспомогательной (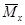) балок;
· вычисляем интеграл Мора для всей балки по соответствующим участкам;
· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.
Вычисление интеграла Мора пример
Пусть для шарнирно опертой балки постоянной изгибной жесткости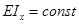 
, длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета (
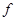) и угол поворота на левой опоре (
).
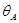определение прогиба с помощью интеграла Мора
В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу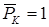 
(рис. 15.7, б).
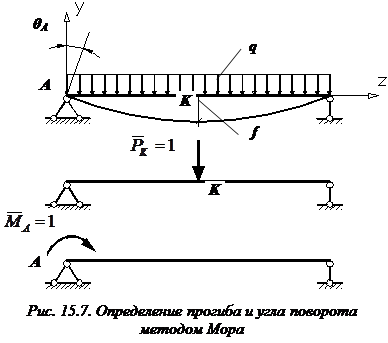Записываем выражения для изгибающих моментов для каждого из двух участков (
) заданной и вспомогательной балок:
.
.
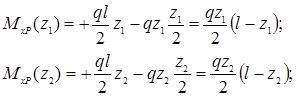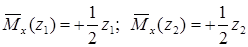Вычисляем интеграл Мора. Учитывая симметрию балки, получим:
.
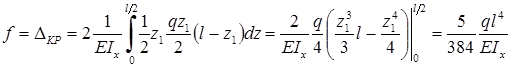Определение угла поворота методом Мора
Нагружаем вспомогательную балку единичным моментом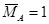 
, прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).
Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка (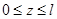
):
;
.
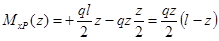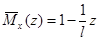Тогда интеграл Мора будет иметь вид:
.
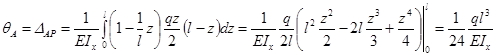Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .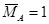
Источник
При сложном сопротивлении в поперечных сечениях стержня действуют шесть внутренних усилий: Nx, Qyy Qz, A/v, My, Mz. В соответствии с принципом независимости действия сил потенциальная энергия упругой деформации равна сумме потенциальной энергии от всех шести внутренних усилий. Запишем потенциальную энергию упругой деформации при сложном сопротивлении, используя выражения, полученные в предыдущих разделах:
В механике есть теорема Кастильяно, позволяющая находить перемещения как производную от потенциальной энергии по обобщенной силе А = дП/dF. Приведем пример использования теоремы Кастильяно.
Для консольной балки, нагруженной силой на конце, изгибающий момент в произвольном сечении х равен М = Fx.
Потенциальная энергия упругой деформации
Перемещение под силой
Если необходимо определить перемещение в точке, где нс приложено никакой силы, надо в этой точке приложить фиктивную силу —»0 настолько малую, чтобы она не изменила величину перемещения от других сил. Тогда изгибающий момент в произвольном сечении равен сумме изгибающих моментов от внешних сил и от фиктивной силы F&:
где М — изгибающий момент от = 1, так как внутренние усилия пропорциональны приложенной силе FПоскольку реально фиктивной силы нет, в выражении для перемещения надо положить /•’ф = 0. Тогда перемещение точки приложения фиктивной силы
Последнее выражение есть частный случай интеграла Мора для изгиба балок. По аналогии: при растяжении продольное усилие N = NF + F^N , где N — продольное усилие от F^ = 1; при кручении крутящий момент Л/к = MkF + F.MK, где Мк — крутящий момент от ^Ф=1-
Проделав описанные выше преобразования, получаем выражения для расчета перемещений при растяжении и при кручении. В общем случае при действии шести внутренних усилий перемещение в точке, где приложена фиктивная сила
Это выражение представляет собой интеграл Мора для определения перемещения в самом общем случае нагружения (при сложном сопротивлении). В этом выражении Nxf, Qyfy QzF, MyF, MzF, MkF — внутренние усилия_в произвольном сечении от действия всех внешних сил, Nx, Qy , Q4, Му, М,, Мк — внутренние усилия в произвольном сечении от действия /1 = 1 (от единичной силы).
Каждый интеграл вносит свой вклад в перемещение, но этот вклад различный. Если есть хоть один момент (изгибающий или крутящий), то влиянием первых трех слагаемых (от продольного усилия и от поперечных сил) можно пренебречь.
На практике не приходится рассчитывать все шесть интегралов. При растяжении—сжатии используют только первый интеграл (в сечениях действует только продольное усилие 7VX), при кручении — только шестой интеграл. При плоском изгибе влиянием поперечной силы можно пренебречь, тогда в расчет включается только один пятый интеграл от изгибающего момента. При сложном сопротивлении учитывают три интеграла от двух изгибающих моментов и крутящего момента.
Интеграл Мора можно использовать для определения перемещений как прямолинейных, так и криволинейных стержневых систем. Поскольку интеграл Мора вычисляется по длине, для криволинейных стержней вместо 6х в подынтегральном выражении используется элемент длины дуги ds = pdcp, где р — радиус кривизны стержня. Он может быть постоянным, а может быть функцией от угловой координаты (р.
Перепишем выражение (11.1) в общем виде, справедливом как для прямолинейных, так и для криволинейных стержней:
где 6s = dx — для прямолинейных стержней и 6s = рбф — для криволинейных стержней.
Пример. Для консольной балки с помощью интегршга Мора найти прогиб посередине балки Дд и угол поворота конца балки Q0.
Балку, нагруженную внешней силой F, будем называть грузовой системой (рис. 11.2, а). Нарисуем балку, нагруженную единичной силой в точке, где ищем перемещение. Назовем ее единичной системой. Поскольку ищем два перемещения, для каждого перемещения надо нарисовать свою единичную систему.
Для определения линейного перемещения (рис. 1J.2, б) единичную систему нагружают сосредоточенной единичной силой F = 1, для определения угла поворота сечения (рис. 11.2, в) единичную систему нагружают единичным моментом М = 1. Разобьем балку на два участка. Произвольные сечения на этих участках обозначим х, и х2. Запишем изгибающие моменты на каждом участке от внешних и от единичных сил:
Подставляем найденные выражения для изгибающих моментов под интеграл Мора:
Рис. 11.2. Грузовая (а) и единичные (б, в) системы для вычисления перемещений
консольной балки
Источник
|
Макеты страниц
Вывод основной формулы. Определение прогибов. Пусть к балке в точке (рис. 20) приложена сила Р, которая равна единице (единичная сила). Если сообщить балке некоторый дополнительный прогиб у, то работа внешней силы у (а) будет равна работе внутренних сил упругости .
Обозначим изгибающий момент в сечении стержня от действия единичной силы . Пусть — относительный поворот двух близких сечений, возникший в результате дополнительного прогиба у балки. Тогда работа внутренних сил (работа деформации, рис. 21)
Приравнивая работы внешних и внутренних сил, получаем
Уравнение (40) должно быть справедливым для произвольного (малого) прогиба стержня.
Предположим теперь, что в качестве у рассматривается прогиб от внешней нагрузки.
Тогда
где — изгибающий момент в сечении от действия внешней нагрузки.
Подставляя отсюда значение в соотношение (40), получаем основную расчетную формулу (интеграл Мора)
Следовательно, чтобы найти прогиб в данном сечении стержня, надо приложить единичную силу в этом сечении, определить изгибающий момент от единичной силы и вычислить интеграл (41).
Величина в , так как в равенстве (41) сокращен множитель 1 Н. Единичный силовой фактор при использовании интеграла Мора
Рис. 21. Работа внутренних силовых факторов
следует считать безразмерной величиной (момент от единичной силы имеет размерность длины).
В большинстве практических задач интеграл Мора определяют с помощью правила Верещагина (см. ннже).
В общем случае интеграл Мора может быть вычислен по правилу трапеций. Равенство (41) справедливо и для упругопластических деформаций, если соответствующим образом определить
Если требуется учесть влияние перерезывающей силы на прогиб, то уравнение (40) будет иметь вид
где — угол сдвига [см. формулу (32)]; — перерезывающая сила в сечении от действия единичной силы.
Вместо равенства (41) будем иметь
Второй член в этой формуле выражает прогиб от действия перерезывающей силы.
Преимущества определения перемещения с помощью интеграла Мора особенно сказываются для стержней с непрямолинейной осью. Пусть, например, требуется найти проекцию перемещения точки А (рис. 22) на направление I—I, причем следует учесть влияние изгибающих моментов, перерезывающих и нормальных сил.
Повторяя предыдущие рассуждения,
Рис. 22. Изгиб Г-образного стержня
Найдем проекцию перемещения точки приложения единичной силы на ее направление:
где — изгибающий момент, перерезывающая и нормальная силы в сечении стержня от действия единичной силы, — то же в поперечном сечении от действия внешних
Интегрирование распространяется на всю длину осн стержня, элемент длины обозначается
Определение углов поворота. Формула для определения углов поворота выводится так же, как соотношение (44). В сечении, где определяют угол поворота, прикладывают единичный момент (рис. 23). Работа момента будет .
В соответствии с этим
В этом равенстве — изгибающий момент в сечении стержня от действия единичного момента.
Рис. 23. (см. скан) Работа единичного момента
Вычисление интеграла Мора по правилу Верещагина. Изгибающий момент от внешней нагрузки и изгибающий момент от единичной силы (момента) определяют по одному правилу знаков (например, момент считают положительным, если он создает сжатие верхнего волокна).
Если при вычислении интеграла (41) или (45) получается отрицательная величина, это означает, что действительный прогиб или угол поворота сечения направлен в сторону, противоположную направлению соответственно единичной силы или единичного момента.
Эпюра изгибающих моментов от единичной силы или единичного момента состоит из отрезков прямых. Рассмотрим участок стержня в пределах от до (рис. 24).
Предположим, что изгибающий момент от единичной нагрузки выражается равенством
где А и В — некоторые числа. Тогда интеграл Мора на рассматриваемом участке
Рис. 24. К выводу правила Верещагина
Предположим, что жесткость стержня на изгиб в пределах участка постоянна, и учтем, что
где — площадь эпюры изгибающих моментов от внешних сил.
Тогда
Далее следует прииить во внимание, что
так как интеграл представляет собой статический момент площади , а гц — абсцисса центра тяжести площади
Формула (48) справедлива в том случае, когда величина имеет постоянный знак в пределах участка.
Используя соотношение (48), получим из равенства (47)
Рис. 25. (см. скан) Ограничения для применения правила Верещагина
где — момент от единичной нагрузки в сечении гц.
Следовательно, интеграл Мора в пределах участка равен произведению площади эпюры моментов от внешних сил на ординату эпюры от единичной нагрузки в сечении, соответствующем центру тяжести этой площади, деленному на жесткость стержня на изгиб (правило Верещагина).
1. Площадь и положение центра тяжести эпюр
(см. скан)
Ограничения для применения правила Верещагина. 1. Эпюра изгибающего момента от единичной нагрузки должна быть в виде одной прямой линии. На рис. 25, а показан случай, когда это условие не соблюдается. Интеграл необходимо вычислять отдельно для участков I и II.
2. Изгибающий момент от внешней нагрузки в пределах участка должен иметь один знак. На рис. 25, б показан случай, когда правило Верещагина следует применять для каждого из двух участков в отдельности.
Ограничение не распространяется на момент от единичной нагрузки.
3. Жесткость стержня на изгиб в пределах участка должна быть постоянна. На рис. 25, в приведен случай, когда интеграл нужно вычислить отдельно для участков и II. Вспомогательные данные для применения правила Верещагина приведены в табл. 1.
Если эпюра от внешних силовых факторов на данном участке является линейной (например, при действии сосредоточенных сил и моментов), то равенство (46) можно использовать для момента и тогда, повторяя вывод, найдем
где — площадь эпюры моментов от единичной нагрузки; — ордината эпюры моментов от внешних нагрузок в сечении, соответствующем центру тяжести площади эпюры моментов от
единичной иагрузкн. Все ограничения, указанные выше для формулы (49), соответствующим образом переносятся на формулу (50).
Источник
Универсальный метод определения перемещений (линейных перемещений и углов поворота), возникающих в любой стержневой системе от произвольной нагрузки, имеет особенно большое значение для расчета статически неопределимых систем.
Рис. 5.14
Рассмотрим два состояния системы. В первом состоянии на нее действует любое число каких угодно сил и моментов (рис. 5.14, а). Во втором состоянии к системе приложена одна лишь сосредоточенная сила (рис. 5.14, б).
Составим выражение работы силы на перемещении возникающем от сил первого состояния:
Выразим (в случае плоской задачи) через внутренние усилия в стержнях системы [с помощью формул (5.17) и (5.20)]:
Условимся, что черточки над указывают на то, что эти внутренние усилия вызваны действием силы, равной единице.
Таким образом, перемещение от любой нагрузки с помощью формулы (5.22) можно выразить через внутренние усилия, возникающие в заданной системе от этой нагрузки и возникающие в ней от единичной силы. Направление единичной силы совпадает с направлением определяемого перемещения. Если определяется линейное
смещение (например, прогиб какой-либо точки оси стержня), то единичная сила представляет собой безразмерную сосредоточенную силу, приложенную в этой точке; если же определяется угол поворота поперечного сечения в какой-либо точке оси стержня, то единичная сила представляет собой сосредоточенный момент (также безразмерный), приложенный в этой точке.
Состояние сооружения, вызванное действием единичной силы, называется единичным состоянием (или фиктивным). В отличие от него состояние, вызванное действием заданной нагрузки, называется действительным (или грузовым).
Иногда цифровые индексы 1 и 2 в формуле (5.22) заменяются буквенными, например , тогда эта формула принимает вид
где — перемещение по направлению «силы» вызванное действием нагрузки (группы «сил» ).
При размерах поперечных сечений каждого стержня системы, постоянных по длине этого стержня, выражение (5.23) принимает вид
Каждое из равенств (5.22) — (5.24) носит название формулы перемещений (интеграла, или формулы, Мора).
Определение перемещений с помощью полученной формулы производится в следующем порядке:
1) находятся выражения усилий от заданной нагрузки как функции координаты произвольного сечения;
2) по направлению искомого перемещения прикладывается соответствующая ему единичная сила (при линейном перемещении — сосредоточенная сила, при угле поворота — сосредоточенный момент);
3) определяются усилия от единичной силы как функции координаты произвольного сечения;
4) найденные выражения усилий подставляются в правую часть формулы (5.23) или (5.24) и интегрированием по участкам в пределах всего сооружения определяется искомое перемещение Если положительно, то перемещение совпадает с направлением единичной силы, а если отрицательно, то противоположно этому направлению.
В случае, если элемент конструкции представляет собой брус малой кривизны, определение перемещений может выполняться по формуле Мора, полученной для прямого бруса, с заменой элемента длины в подынтегральном выражении элементом дуги
Иногда, в частности при расчете статически неопределимых систем, приходится определять взаимные перемещения отдельных
точек или сечений сооружений. В этом случае в направлении искомого перемещения прикладывается обобщенная единичная сила (при определении линейного перемещения) или обобщенный единичный момент (при определении взаимного угла поворота). Например, если требуется определить изменение расстояния между точками С и D оси рамы, изображенной на рис. 5.15, а, то следует в точках С и D приложить единичные силы, направленные по линии CD, как показано на рис. 5.15, б. Вычисление интеграла Мора производится по изложенным выше правилам, но при этом под единичными внутренними усилиями понимаются их значения, соответствующие одновременному действию обеих единичных сил.
Рис. 5.15
В рассматриваемом случае, если результат вычислений интеграла Мора получится положительным, то это будет указывать на то, что направление искомого перемещения совпадает с направлением единичных сил, т. е. расстояние между точками С и D увеличивается; знак минус указывает на уменьшение этого расстояния, т. е. на сближение точек С и
Аналогично можно определить взаимный угол поворота любых двух сечений рамы, например сечений, соответствующих тем же точкам С и D. Для этого в указанных сечениях надо приложить единичные моменты, действующие в противоположных направлениях (рис. 5.15, в). В остальном вычисление перемещения производится обычным порядком.
Практически в большинстве случаев плоской задачи используется лишь один член формулы перемещений, а именно, если рассматриваются сооружения, преимущественно работающие на изгиб (балки, рамы, а часто и арки), то в формуле перемещений с соблюдением вполне достаточной точности можно оставить только интеграл, зависящий от изгибающих моментов. При расчете сооружений, элементы которых работают в основном на центральное растяжение и сжатие (например, ферм), можно не учитывать деформации изгиба и сдвига; в соответствии с этим в формуле перемещений оставляется лишь член, содержащий продольные силы. В случае пространственной задачи формула перемещений (интеграл Мора) содержит не три члена (как в случае плоской задачи), а шесть — в соответствии с числом внутренних усилий, которые могут возникать
в поперечных сечениях элементов. Эта формула имеет вид
где изгибающие моменты относительно осей и у поперечных сечений соответственно, возникающие в единичном состоянии; — то же, в действительном состоянии; — поперечные силы, параллельные соответственно осям и у по перечного, сечения, возникающие в единичном состоянии; — то же, в действительном состоянии; — крутящие моменты, возникающие в единичном и 1 действительном состояниях соответственно; — продольные силы в этих же состояниях; — геометрическая характеристика крутильной жесткости (см. § 6.6): при круглом поперечном сечении где полярный момент инерции.
Рис. 5.16
Практически в большинстве случаев пространственной задачи используются или только три первых члена последней формулы (когда элементы системы работают преимущественно на изгиб и кручение, например при расчете пространственных рам и ломаных балок), или только четвертый член формулы (например, при расчете пространственных ферм).
В дальнейшем при расчете балок и рам влияние продольных и поперечных сил на перемещение не учитывается, за исключением особо отмеченных случаев.
Рассмотрим в качестве примера балку постоянного сечения, свободно лежащую на двух опорах (рис. 5.16, а) и нагруженную посередине силой Определим прогиб балки под силой с учетом влияния всех членов формулы Мора (5.24).
Единичным состоянием является состояние, вызванное единичным грузом действующим на балку в направлении искомого перемещения (рис. 5.16, б).
Продольные силы, возникающие в поперечных сечениях балки от нагрузки, равны нулю. Поэтому второй интеграл формулы (5.24) равняется нулю и эта формула принимает вид
где — прогиб, обусловленный деформацией изгиба (т. е. зависящий от изгибающих моментов):
— прогиб, обусловленный деформацией сдвига (т. е. зависящий от поперечных сил):
Для сечений балки в пределах от левой опоры до середины балки изгибающие моменты и поперечные силы равны:
Эпюры изображены на рис. 5.16, в, г, д, е.
Эпюры построены на сжатых волокнах балки.
Подставим значения моментов и поперечных сил в выражения для
Интегрирование ведется в пределах левой половины балки; числовые коэффициенты 2 перед интегралами учитывают, что ввиду симметрии балки величина интеграла для правой ее половины такая же, как и для левой.
Полный прогиб
Знак плюс указывает на то, что направление прогиба совпадает с направлением единичной силы.
Найдем соотношение между прогибами, зависящими от поперечных сил и изгибающих моментов. Предположим при этом, что рассматриваемая балка имеет прямоугольное поперечное сечение со сторонами b и h и что
Подставив в последнюю формулу значения и приняв получим
т. е. прогиб, вызванный деформацией сдвига, составляет только 3% от прогиба, вызванного деформацией изгиба.
Влияние поперечных сил на прогиб тем меньше, чем меньше отношение . Так, при
Совершенно очевидно, что величиной по сравнению с можно пренебречь. Тогда
Этот результат совпадает с результатом, известным из курса сопротивления материалов.
Источник