Интеграл мора для растяжения


 Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.
Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.
Получение формулы интеграла Мора
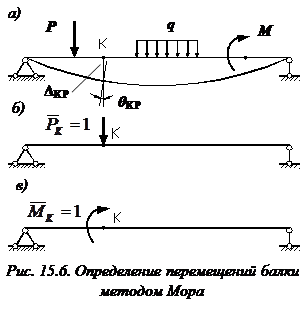
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим 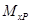 и
и 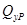 , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки (
, соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки (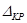 ) в точке K.
) в точке K.
Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой  (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.
(рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.
Внутренние усилия, возникающие во вспомогательной балке, обозначим 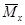 и
и 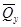 .
.
Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда 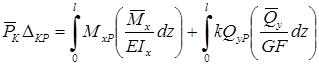 .
.
При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).
Тогда, учитывая, что  , окончательно получим формулу интеграла Мора:
, окончательно получим формулу интеграла Мора: 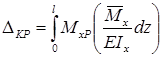 .
.
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора, а саму формулу – интегралом Мора.
Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (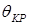 ), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент
), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент 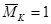 (рис. 15.6, в).
(рис. 15.6, в).
порядок вычисления перемещений методом Мора:
· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу  , а при определении угла поворота – единичный момент
, а при определении угла поворота – единичный момент 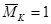 ;
;
· для каждого участка балки составляем выражения для изгибающих моментов заданной (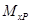 ) и вспомогательной (
) и вспомогательной (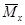 ) балок;
) балок;
· вычисляем интеграл Мора для всей балки по соответствующим участкам;
· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.
Вычисление интеграла Мора пример
Пусть для шарнирно опертой балки постоянной изгибной жесткости 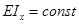 , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета (
, длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета (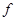 ) и угол поворота на левой опоре (
) и угол поворота на левой опоре (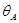 ).
).
определение прогиба с помощью интеграла Мора
В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу 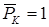 (рис. 15.7, б).
(рис. 15.7, б).
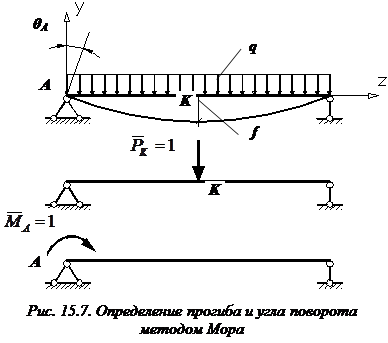 Записываем выражения для изгибающих моментов для каждого из двух участков (
Записываем выражения для изгибающих моментов для каждого из двух участков ( ) заданной и вспомогательной балок:
) заданной и вспомогательной балок:
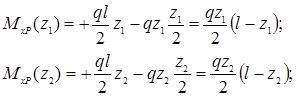 .
.
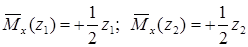 .
.
Вычисляем интеграл Мора. Учитывая симметрию балки, получим:
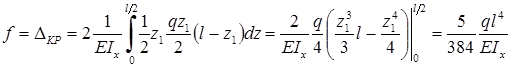 .
.
Определение угла поворота методом Мора
Нагружаем вспомогательную балку единичным моментом 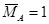 , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).
, прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).
Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка (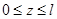 ):
):
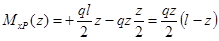 ;
;
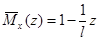 .
.
Тогда интеграл Мора будет иметь вид:
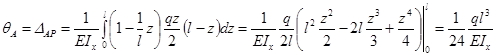 .
.
Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента 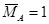 .
.
Источник
Содержание:
- Пример решения задачи 2.2.
- Пример решения задачи 2.3.
- Пример решения задачи 3.1.
- Пример решения задачи 3.2.
Метод Максвелла — Мора представляет собой универсальный способ для определения линейных и угловых перемещений в любых плоских и пространственных системах.
- Напомним основные этапы использования метода Максвелла -Мора.
При отыскании линейного перемещения к системе, освобожденной от заданных нагрузок, в направлении искомого перемещения (в заданной точке) прикладывается безразмерная единичная сила. Аналогично, при определении углового перемещения в сечении, поворот которого требуется найти, прикладывается пара сил (в плоскости искомого поворота) с моментом, равным безразмерной единице.
Строятся эпюры внутренних силовых факторов от заданной нагрузки и единичных воздействий.
По этой ссылке вы найдёте полный курс лекций по сопротивлению материалов:
Искомое перемещение определяется из выражения:

правую часть, которого называют интегралами Мора, где:  искомое перемещение (линейное или угловое). Первый индекс указывает номер искомого перемещения
искомое перемещение (линейное или угловое). Первый индекс указывает номер искомого перемещения  второй индекс
второй индекс  указывает причины, вызывающие деформации отдельных элементов системы и как следствие , перемещение
указывает причины, вызывающие деформации отдельных элементов системы и как следствие , перемещение  (индекс
(индекс  указывает, что перемещение определяется от заданной нагрузки);
указывает, что перемещение определяется от заданной нагрузки);
 аналитические выражения продольной, поперечной сил и изгибающего момента соответственно от единичного и заданного воздействия (единичные и грузовые эпюры внутренних усилий);
аналитические выражения продольной, поперечной сил и изгибающего момента соответственно от единичного и заданного воздействия (единичные и грузовые эпюры внутренних усилий);
 жесткости поперечных сечений стержня соответственно на растяжение, сдвиг, изгиб;
жесткости поперечных сечений стержня соответственно на растяжение, сдвиг, изгиб;
 коэффициент отражает неравномерность распределения касательных напряжений по поперечному сечению. Этот коэффициент зависит от формы сечения, например, для прямоугольника
коэффициент отражает неравномерность распределения касательных напряжений по поперечному сечению. Этот коэффициент зависит от формы сечения, например, для прямоугольника  для круга
для круга 
Направление единичного воздействия выбирается произвольно. Полученный по формуле (2.1) положительный результат указывает на то, что направление искомого перемещения совпадает с принятым направлением единичного воздействия, либо противоположно принятому направлению, если получен отрицательный результат.
В формуле (2.1) каждый интеграл четко выражает вклад соответствующей деформации в искомое перемещение. Обычно учитываются лишь основные виды деформации. В конструкциях работающих на изгиб учитывается влияние изгибающих моментов, а поперечными силами пренебрегают.
В комбинированных системах, где часть стержней работает на растяжение-сжатие, а часть — на изгиб, учитываются обе эти деформации. В фермах, где каждый стержень работает на растяжение -сжатие в формуле (2.1) остается только первый интеграл.
В случаях, когда ось бруса прямолинейна и жесткость поперечного сечения в пределах отдельных участков постоянна, интегралы
Мора, входящие в выражение (2.1) целесообразно вычислять, используя правило Верещагина или формулу Симпсона.
Возможно вам будут полезны данные страницы:
Пример решения задачи 2.2.
Определить прогиб конца консольной балки (рис. 2.2,а), учитывая лишь деформации, изгиба, жесткость поперечного сечения балки постоянна. 
Решение:
Эпюра изгибающих моментов от заданной нагрузки показана на рис. 
Построим единичную эпюру, для этой цели, сняв с балки заданную нагрузку, приложим к концу консоли (точка  рис. 2.2 в),
рис. 2.2 в),
вертикально направленную единичную силу  , направление
, направление
единичной силы выбирается произвольно , например направим ее вниз, т.е. предполагаем , что точка  переместится вниз по отношению продольной оси балки .
переместится вниз по отношению продольной оси балки .
При заданном загружении (рис. 2.2,в), балка имеет один участок  Единичный изгибающий момент для произвольного сечения
Единичный изгибающий момент для произвольного сечения  участка будет равен
участка будет равен 
Подставляя в полученное уравнение прямой координаты начала и конца участка, построим единичную эпюру изгибающих моментов (рис. 2.2, г ).
Для определения прогиба точки  надо «перемножить» эпюры от заданной нагрузки и от единичной силы. Проделаем это. Балка имеет два участка,
надо «перемножить» эпюры от заданной нагрузки и от единичной силы. Проделаем это. Балка имеет два участка,  На участке
На участке  интеграл Мора вычислим по способу Верещагина.
интеграл Мора вычислим по способу Верещагина.

Перемещение положительно, так как обе сопрягаемые эпюры, лежат по одну сторону от базы ( продольной оси бруса ).
На участке  грузовая эпюра нелинейная и заранее неизвестно, где находится ее центр тяжести, использовать правило Верещагина на этом участке затруднительно. Для вычисления интеграла Мора на участке
грузовая эпюра нелинейная и заранее неизвестно, где находится ее центр тяжести, использовать правило Верещагина на этом участке затруднительно. Для вычисления интеграла Мора на участке  воспользуемся формулой Симпсона. Применяя ее, найдем:
воспользуемся формулой Симпсона. Применяя ее, найдем:

Прогиб сечения  равняется сумме интегралов Мора на участках
равняется сумме интегралов Мора на участках 

Знак плюс прогиба  указывает на то, что сечение переместится по направлению единичной силы, т.е. вниз.
указывает на то, что сечение переместится по направлению единичной силы, т.е. вниз.
Пример решения задачи 2.3.
Определить угол поворота сечения  двухопорной балки с консолью (рис. 2.3,а), учитывая лишь деформации изгиба, жесткость, балки постоянна.
двухопорной балки с консолью (рис. 2.3,а), учитывая лишь деформации изгиба, жесткость, балки постоянна.
Решение:
Эпюра изгибающих моментов от заданной нагрузки построена ранее в примере, ее вид показан (рис. 2.3, б).
Построим единичную эпюру, для этой цели, сняв с балки заданую нагрузку, приложим в сечении  единичный момент
единичный момент  направление единичного момента выбираем произвольно, например по ходу часовой стрелки (рис. 2.3,в).
направление единичного момента выбираем произвольно, например по ходу часовой стрелки (рис. 2.3,в).
Балка имеет три участка. Сопряжение эпюр проведем по участкам. На первом участке (участок  для вычисления угла поворота, используем формулу Симпсона, так как эпюра
для вычисления угла поворота, используем формулу Симпсона, так как эпюра  на участке интегрирования нелинейная:
на участке интегрирования нелинейная:

На втором участке (участок
обе эпюры изгибающих моментов линейны.
Поэтому интеграл Мора на этом участке можно вычислить по формуле трапеций. Применяя ее, найдем:

Полученные выражения отрицательны потому, что знаки ординат «перемножаемых» эпюр  противоположны. На третьем участке (участок
противоположны. На третьем участке (участок  интеграл Мора вычислим способом Верещагина:
интеграл Мора вычислим способом Верещагина:

Получен отрицательный результат потому, что эпюры  и
и  лежат по разные сторону от базы ( продольной оси бруса ). Угол поворота сечения
лежат по разные сторону от базы ( продольной оси бруса ). Угол поворота сечения  равняется сумме интегралов Мора на трех участках ( на участках
равняется сумме интегралов Мора на трех участках ( на участках 

Полученный знак минус указывает на то, что сечение  поворачивается в направлении, противоположном направлению единичного момента.
поворачивается в направлении, противоположном направлению единичного момента.
Пример решения задачи 3.1.
Для консольной рамы, рис. 3.1,а, определить вертикальное и горизонтальное перемещение точки  а также угол поворота узла
а также угол поворота узла  жесткости стержней
жесткости стержней 
Решение:
Поскольку при определении перемещений в рамах используется интеграл Мора, содержащий изгибающие моменты, построение эпюр  не обязательно.
не обязательно.
Построим грузовую эпюру изгибающих моментов, её вид показан на рис. 3.1,6.
Для определения вертикального и горизонтального перемещение точки  в это сечение приложим единичные силы
в это сечение приложим единичные силы  и
и
 построим единичные эпюры, их вид показан на рисунках
построим единичные эпюры, их вид показан на рисунках
«Перемножим» грузовую и единичные эпюры в пределах длины каждого участка (стержня).
 Вертикальное перемещение точки
Вертикальное перемещение точки 

Горизонтальное перемещение точки 

Анализируя, полученные выражения, устанавливаем, что точка  перемещается вверх и влево.
перемещается вверх и влево.
Для определения угла поворота узла  в этот узел приложим единичный момент
в этот узел приложим единичный момент  и построим единичную эпюру изгибающих моментов, см. рис. 3.1,д.
и построим единичную эпюру изгибающих моментов, см. рис. 3.1,д.
«Перемножая» грузовую и единичную эпюры, определим угол поворота узла 

Сечение поворачивается против хода часовой стрелки.
Пример решения задачи 3.2.
Для шарнирно опертой рамы со стержнями различной жесткости, рис. 3.2,а, определить горизонтальное перемещение точки  и угол поворота сечения
и угол поворота сечения 
Решение:
Определим опорные реакции от действия заданных нагрузок.

Строим грузовую эпюру изгибающих моментов (рис. 3.2,6).
 Приложим в точке
Приложим в точке  горизонтальную единичную силу
горизонтальную единичную силу  а в сечение
а в сечение  единичный момент
единичный момент  и построим
и построим
единичные эпюры изгибающих моментов, см. рис. 3.2,в,г. «Перемножив» эти эпюры с грузовой эпюрой  получим:
получим:

Точка  перемещается вправо, а сечение
перемещается вправо, а сечение  поворачивается по ходу часовой стрелки.
поворачивается по ходу часовой стрелки.
Источник
В общем случае (стержень переменного сечения, сложная система нагрузок) интеграл Мора определяется путем численного интегрирования. Во многих практически важных случаях, когда жесткость сечения постоянна по длине стержня, интеграл Мора может быть вычислен по правилу Верещагина. Рассмотрим определение интеграла Мора на участке от а до 6 (рис. 9.18).
Рис. 9.18. Правило Верещагина для вычисления интеграла Мора
Эпюры момента от единичного силового фактора состоят из отрезков прямых. Не нарушая общности, предположим, что в пределах участка
где А и В — параметры прямой:
Интеграл Мора на рассматриваемом участке постоянного сечения имеет вид
при этом
где F — площадь под кривой (площадь эпюры изгибающих моментов от внешних сил на участке z).
Далее следует учесть, что статический момент площади эпюры моментов равен
где — абсцисса центра тяжести площади .
Равенство (109) справедливо, когда в пределах участка не изменяет знак и может рассматриваться как элемент площади эпюры. Теперь из соотношений (107) —(109) получаем
где
— момент от единичной нагрузки в сечении
Вспомогательная таблица для использования правила Верещагина дана на рис. 9.19.
Замечания. 1. Если эпюра от действия внешних сил на участке линейна (например, при действии сосредоточенных сил и моментов), то правило можно применять в обращенном виде: площадь эпюры от единичного силового фактора умножить на ординату эпюры соответствующую центру тяжести площади . Это вытекает из приведенного доказательства.
2. Правило Верещагина может быть распространено на интеграл Мора в общем виде (уравнение (103)).
Рис. 9.19. Площади и положение центров тяжести эпюр моментов
Рис. 9.20. Примеры определения прогиба и углов поворота по правилу Верещагина
Основное требование при этом состоит в следующем: в пределах участка внутренние силовые факторы от единичной нагрузки должны быть линейными функциями вдоль оси стержня (линейность эпюр!).
Примеры. 1. Определить прогиб в точке А консольного стержня при действии сосредоточенного момента М (рис. 9.20, а).
Прогиб в точке А определяем по формуле (для краткости индекс опускается)
Знак минус связан с тем, что имеют разные знаки.
2. Определить прогиб в точке А в консольном стержне под действием распределенной нагрузки.
Прогиб определяем по формуле
Эпюры изгибающего момента М и перерезывающей силы Q от внешней нагрузки показаны на рис. 9.20, б, ниже на этом рисунке приведены эпюры при действии единичной силы. Далее находим
3. Определить прогиб в точке А и угол поворота в точке В для двухопорной балки, загруженной сосредоточенным моментом (рис. 9.20.).
Прогиб определяем по формуле (деформацией сдвига пренебрегаем)
Так как эпюра момента от единичной силы не изображается одной линией; то интеграл разбиваем на два участка:
Угол поворота в точке В равен
Замечание. Из приведенных примеров видно, что способ Верещагина в простых случаях позволяет быстро определить прогибы и углы поворота. Важно только применять единое правило знаков для Если условиться при изгибе стержня строить эпюры изгибающих моментов на «растянутом волокне» (см. рис. 9.20), то сразу легко видеть положительные и отрицательные значения моментов.
Особое преимущество правила Верещагина состоит в том, что оно может быть исполъвовано не только для стержней, но и для рам (разд. 17).
Ограничения для применения правила Верещагина.
Эти ограничения вытекают из вывода формулы (110), но обратим на них внимание еще раз.
1. Эпюра изгибающего момента от единичной нагрузки должна быть в виде одной прямой линии. На рис. 9.21, а показан случай, когда это условие не соблюдается. Интеграл Мора необходимо вычислять отдельно для участков I и II.
2. Изгибающий момент от внешней нагрузки в пределах участка должен иметь один знак. На рис. 9.21, б показан случай, когда правило Верещагина следует применять для каждого участка в отдельности. Это ограничение не относится к моменту от единичной нагрузки.
Рис. 9.21. Ограничения при использовании правила Верещагина: а — эпюра шсеет излом; б — эпюра имеет разные знаки; в — стержень имеет разные сечения
3. Жесткость стержня в пределах участка должна быть постоянна, иначе интегрирование следует распространять отдельно на участки с постоянной жесткостью. Ограничения по постоянной жесткости можно избежать, если строить эпюры .
Источник
При сложном сопротивлении в поперечных сечениях стержня действуют шесть внутренних усилий: Nx, Qyy Qz, A/v, My, Mz. В соответствии с принципом независимости действия сил потенциальная энергия упругой деформации равна сумме потенциальной энергии от всех шести внутренних усилий. Запишем потенциальную энергию упругой деформации при сложном сопротивлении, используя выражения, полученные в предыдущих разделах:

В механике есть теорема Кастильяно, позволяющая находить перемещения как производную от потенциальной энергии по обобщенной силе А = дП/dF. Приведем пример использования теоремы Кастильяно.
Для консольной балки, нагруженной силой на конце, изгибающий момент в произвольном сечении х равен М = Fx.
Потенциальная энергия упругой деформации

Перемещение под силой
Если необходимо определить перемещение в точке, где нс приложено никакой силы, надо в этой точке приложить фиктивную силу —»0 настолько малую, чтобы она не изменила величину перемещения от других сил. Тогда изгибающий момент в произвольном сечении равен сумме изгибающих моментов от внешних сил и от фиктивной силы F&:


где М — изгибающий момент от = 1, так как внутренние усилия пропорциональны приложенной силе FПоскольку реально фиктивной силы нет, в выражении для перемещения надо положить /•’ф = 0. Тогда перемещение точки приложения фиктивной силы

Последнее выражение есть частный случай интеграла Мора для изгиба балок. По аналогии: при растяжении продольное усилие N = NF + F^N , где N — продольное усилие от F^ = 1; при кручении крутящий момент Л/к = MkF + F.MK, где Мк — крутящий момент от ^Ф=1-
Проделав описанные выше преобразования, получаем выражения для расчета перемещений при растяжении и при кручении. В общем случае при действии шести внутренних усилий перемещение в точке, где приложена фиктивная сила

Это выражение представляет собой интеграл Мора для определения перемещения в самом общем случае нагружения (при сложном сопротивлении). В этом выражении Nxf, Qyfy QzF, MyF, MzF, MkF — внутренние усилия_в произвольном сечении от действия всех внешних сил, Nx, Qy , Q4, Му, М,, Мк — внутренние усилия в произвольном сечении от действия /1 = 1 (от единичной силы).
Каждый интеграл вносит свой вклад в перемещение, но этот вклад различный. Если есть хоть один момент (изгибающий или крутящий), то влиянием первых трех слагаемых (от продольного усилия и от поперечных сил) можно пренебречь.
На практике не приходится рассчитывать все шесть интегралов. При растяжении—сжатии используют только первый интеграл (в сечениях действует только продольное усилие 7VX), при кручении — только шестой интеграл. При плоском изгибе влиянием поперечной силы можно пренебречь, тогда в расчет включается только один пятый интеграл от изгибающего момента. При сложном сопротивлении учитывают три интеграла от двух изгибающих моментов и крутящего момента.
Интеграл Мора можно использовать для определения перемещений как прямолинейных, так и криволинейных стержневых систем. Поскольку интеграл Мора вычисляется по длине, для криволинейных стержней вместо 6х в подынтегральном выражении используется элемент длины дуги ds = pdcp, где р — радиус кривизны стержня. Он может быть постоянным, а может быть функцией от угловой координаты (р.
Перепишем выражение (11.1) в общем виде, справедливом как для прямолинейных, так и для криволинейных стержней:

где 6s = dx — для прямолинейных стержней и 6s = рбф — для криволинейных стержней.
Пример. Для консольной балки с помощью интегршга Мора найти прогиб посередине балки Дд и угол поворота конца балки Q0.
Балку, нагруженную внешней силой F, будем называть грузовой системой (рис. 11.2, а). Нарисуем балку, нагруженную единичной силой в точке, где ищем перемещение. Назовем ее единичной системой. Поскольку ищем два перемещения, для каждого перемещения надо нарисовать свою единичную систему.
Для определения линейного перемещения (рис. 1J.2, б) единичную систему нагружают сосредоточенной единичной силой F = 1, для определения угла поворота сечения (рис. 11.2, в) единичную систему нагружают единичным моментом М = 1. Разобьем балку на два участка. Произвольные сечения на этих участках обозначим х, и х2. Запишем изгибающие моменты на каждом участке от внешних и от единичных сил:

Подставляем найденные выражения для изгибающих моментов под интеграл Мора:

Рис. 11.2. Грузовая (а) и единичные (б, в) системы для вычисления перемещений
консольной балки
Источник
