График зависимости силы упругости от растяжения
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.
Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.
Деформация.
Силы упругости возникают при деформациях тел. Деформация — это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб.
Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.
Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.
Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:
1. действует между соседними слоями деформированного тела и приложена к каждому слою;
2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры).
Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил
выходит далеко за рамки школьной программы.
В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.
Закон Гука.
Деформация называется малой, если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.
Закон Гука. Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину , сила упругости даётся формулой:
(1)
где — коэффициент жёсткости пружины.
Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.
Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):
 |
| Рис. 1. Закон Гука |
Коэффициент жёсткости — о угловой коэффициент в уравнении прямой . Поэтому справедливо равенство:
,
где — угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .
Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 — это лишь небольшой начальный участок криволинейного графика, описывающего зависимость от при всех значениях деформации .
Модуль Юнга.
В частном случае малых деформаций стержней имеется более детальная формула, уточняющая общий вид ( 1 ) закона Гука.
Именно, если стержень длиной и площадью поперечного сечения растянуть или сжать
на величину , то для силы упругости справедлива формула:
.
Здесь — модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.
Источник
Что такое сила упругости
Определение
Сила упругости — вид силы, возникающей внутри тела при его упругой деформации, величина которой находится в прямой пропорциональной зависимости от абсолютного значения разницы начальной и конечной длины.
В математических формулах и на схемах она обозначается Fупр и измеряется в международной системе СИ в единицах — Ньютон на метр (Н/м).
Изменение формы тела происходит путем сжатия либо растяжения. Воздействие может быть постепенным и длительным, краткосрочным и резким. Несомненно одно: возникающая в ответ сила (Fупр) стремится вернуть телу первоначальную форму и направлена противоположно первично действующей.
Если деформация является упругой, Fупр тем значительнее, чем больше изменение длины.
Для каждого вещества установлена такая физическая характеристика, как степень жесткости. Именно она определяет, какая сила должна быть приложена к телу, чтобы изменение его формы произошло определенным образом.
Когда возникает и от чего зависит
В принципах объяснения этого явления заложены изменения геометрии межмолекулярных пространств и, соответственно, — сил, удерживающих молекулярные решетки в естественном положении. Другими словами, молекулярная решетка всегда стремится к стабильности. Увеличение либо уменьшение расстояния между молекулами, которые непременно происходят при растяжении либо сжатии, влечет возникновение сопротивления. Его интенсивность прямо пропорциональна величине деформации.
При упругих изменениях формы тела в них появляется потенциальная энергия. Это электромагнитная величина, которую характеризуют как внешнее проявление межмолекулярных сил. Направление вектора этих сил противоположно смещению молекул. Простейшим примером подобной ситуации является растяжение либо сжатие пружины. По мере прекращения воздействия пружина принимает первоначальный вид и в ней исчезает сила упругости.
Такая зависимость нашла свое отражение в законе Гука — постулате, лежащем в основе многих физических процессов.
Пример
Результат проявления Fупр — стрельба из лука, весы на пружине, спортивный инвентарь с пружинным механизмом, белье, вывешенное на веревке, матрац пружинной конструкции и др.
Какой закон описывает силу упругости
Для измерения силы, противодействующей элементарной деформации простого тела, применяется формула:
(F=ktimesDelta l)
где k — коэффициент пропорциональности, зависящий от жесткости материала, Δl — изменение длины тела при деформации под воздействием внешней силы.
Часто перед правой половиной равенства ставится знак «минус», что означает противоположную направленность внешней силы и силы упругости. В вышеизложенном виде значение определяется по модулю.
Это закон Гука, который был открыт ученым в 1660 году и является основным в теории упругости. Он имеет и теоретическую формулировку.
Определение
Закон Гука: та сила, которая действует при деформации тела, находится в прямой пропорциональной зависимости от изменения длины и в момент действия направлена в сторону, противоположную перемещению внутренних частиц.
Примечание
Идеально выполняется закон Гука при малых деформациях, поскольку интенсивная сила может вызвать разрушение вещества, из которого изготовлено тело.
Существует и сугубо физическая формулировка этого закона. В ней задействовано понятие относительной деформации. Формула выглядит так:
(varepsilon=xdiv l)
В то же время
(sigma=Fdiv S=-Fупрdiv S)
где S — площадь сечения тела, подвергшегося деформации, σ — напряжение.
Из этих математических выражений вытекает следующая форма закона Гука:
(varepsilon=(1div E)timessigma)
где E — модуль Юнга, зависящий только от характеристики материала, но не от формы и размеров тел.
График зависимости силы упругости
Получить наглядное представление о зависимости силы упругости от растяжения пружины можно, построив график. Его внешний вид следующий:

График зависимости силы упругости
Получить наглядное представление о зависимости силы упругости от растяжения пружины можно, построив график. Его внешний вид следующий:
Пояснение: ось ординат — значения силы упругости; ось абсцисс — изменения длины.
Масштаб подбирается соответственно разрядности используемых данных.
Построение происходит по обычным геометрическим алгоритмам:
- составляются ряды данных;
- наносятся значения на оси координат, имеющих соответствующее обозначение;
- соединяются полученные точки.
Для наглядности часто график строят таким образом, что максимальное значение одного из параметров соответствует наивысшей точке на прямой.
График в виде прямой линии справедлив для растяжения пружины до определенного (критического) уровня ее растягивания. Если же действующая сила, после достижение этого уровня, продолжает свое воздействие, деформация перестает быть упругой. Другими словами, на воздействие деформирующей силы тело перестает отвечать своими попытками восстановить прежнюю форму. Кроме того, при очень большой силе оно может полностью либо частично разрушиться. В таком случае график приобретает особенность и выглядит так:

Пояснение в следующем: область I — прямая линия, начинающаяся в начале координат — характеризует зависимость между Fупр и удлинением (укорочением) пружины при малых деформациях. Это — область действия закона Гука. Область II характеризует более значительные деформации, проявлением которых может быть разрыв тела. Такие деформации называются пластическими.
Примеры силы упругости в физике
Силу упругости можно наблюдать не только в физических опытах, но и в быту. Именно она является причиной того, что мокрое белье, повешенное на веревку, не падает на землю. Первоначально, под его тяжестью, веревка провисает, но после возвращается практически в прежнее положение. При последующем увеличении массы провисание появляется вновь.
Благодаря силе упругости биологические ткани животных, растений и человека не разрушаются под воздействием окружающей среды, например, атмосферного давления. Еще большую нагрузку испытывают живые организмы, находящиеся под водой.
Условием того, что с веток не падают птицы, на них держатся плоды, ветки не ломаются под порывами ветра и массивными снежными шапками, также является наличие этой силы.
Источник

1. Твёрдые тела под действием силы способны изменять свои форму и (или) объём. Взяв за концы металлическую линейку, можно её согнуть. Если перестать прикладывать силу, то линейка восстановит свою форму. Если сжать пружину (рис. 35), то она сократится, т.е. деформируется. При прекращении действия силы пружина вернётся в первоначальное
состояние.
Изменение формы или объёма тела при действии на него силы называется деформацией.
Если длина пружины в недеформированном состоянии ( l_0 ), а после растяжения ( l ), то изменение её длины ( l=l-l_0=x ), где ( l ) или ( x ) – удлинение или деформация.
2. При деформации в теле возникает сила упругости, которая стремится вернуть его в первоначальное состояние. Сила упругости ( (vec{F}_{упр}) ) — сила, возникающая в теле в результате деформации, стремящаяся вернуть тело в первоначальное состояние и направленная в сторону, противоположную деформации (удлинению).
Так, при растяжении пружины эта сила направлена влево к положению равновесия, при
сжатии пружины сила упругости направлена вправо (рис. 36).
Если тело после прекращения действия силы принимает первоначальную форму, то деформация является упругой. Если тело после прекращения действия силы не принимает первоначальную форму, то деформация является неупругой или пластической.
3. При малых деформациях сила упругости прямо пропорциональна удлинению. Поскольку сила упругости и деформация направлены в противоположные стороны, то: ( F_{упр}=-kDelta l ), где ( k ) — коэффициент пропорциональности, называемый жёсткостью тела. Жёсткость зависит от размеров тела, его формы, материала, из которого сделано тело.
Единица жесткости ( [,k,]=frac{[,F,]}{[,Delta l,]} ); ( [,k,]=frac{1,Н}{1,м}=1frac{Н}{м} ).
Формула ( F_{упр}=-kDelta l ) выражает закон Гука: сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению (деформации) тела и направлена в сторону, противоположную деформации.
Важно понимать, что закон Гука справедлив при малых деформациях.
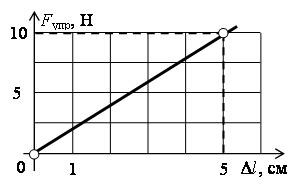
На рисунке 37 приведён график зависимости модуля силы упругости от деформации. Поскольку эта зависимость линейная, то графиком зависимости является прямая, проходящая через начало координат и составляющая угол ( alpha ) с осью абсцисс. По графику можно определить жёсткость тела. Например, значению деформации 2 см соответствует сила упругости 4 Н. Разделив 4 Н на 0,02 м, получим ( k ) = 200 Н/м. В треугольнике АОВ жёсткость ( k ) равна тангенсу угла ( alpha ): ( k=mathrm{tg}alpha ).
4. Существуют разные виды деформации: растяжения, сжатия, сдвига, изгиба и кручения. В рассмотренных примерах линейка подвергалась деформации изгиба, пружина — деформации растяжения и сжатия, винты, гайки, болты при закручивании испытывают деформацию кручения, тяжёлые предметы при перемещении по полу — деформацию сдвига.
5. Предположим, что на полу стоит ящик (рис. 38). На него действует сила тяжести ( vec{F}_т ), направленная вертикально вниз. Ящик, взаимодействуя с полом, деформирует его и деформируется сам. И на ящик, и на пол действует сила упругости, характеризующая их взаимодействие. Сила упругости ( vec{N} ), действующая на ящик со стороны пола, приложена к ящику и направлена вертикально вверх; сила упругости ( vec{P} ), действующая со стороны ящика на пол, приложена к полу и направлена вертикально вниз. Эта сила называется весом тела.
Весом тела называют силу, с которой тело, вследствие его притяжения к Земле, действует на опору или подвес. В отличие от силы тяжести, вес тела приложен не к телу, а к опоре или к подвесу. Вес — это сила упругости.
6. Если тело покоится или движется равномерно и прямолинейно, вес тела численно равен силе тяжести, действующей на него: ( vec{P}=mvec{g} ).
На тело, движущееся вместе с платформой или подвесом вертикально вниз с ускорением ( vec{a} ), направленным в сторону движения, действуют сила тяжести ( vec{F}_{т} ) и сила упругости ( N ) со стороны опоры или подвеса (рис. 39, 40).
Второй закон Ньютона для этой ситуации: ( mvec{g}+vec{N}=mvec{a} ). В проекциях на координатную ось: ( mg-N=ma ) или ( N=mg-ma ). Поскольку ( N=P ), ( P = m(g — a) ).
Если тело движется вниз вместе с опорой или подвесом с ускорением, направленным так же, как и ускорение свободного падения, то его вес меньше силы тяжести, т.е. меньше веса покоящегося тела. Если ускорение тела равно ускорению свободного падения ( vec{a}=vec{g} ), то тело находится в состоянии невесомости.
В таком состоянии находится космонавт в космическом корабле, прыгун с трамплина во время полёта вниз.
7. На тело, движущееся вместе с платформой или подвесом вертикально вверх с ускорением ( vec{a} ), направленным в сторону движения, действуют сила тяжести ( vec{F}_т ) и сила упругости ( vec{N} ) со стороны опоры или подвеса (рис. 40).
Второй закон Ньютона для этой ситуации: ( mvec{g}+vec{N}=mvec{a} ). В проекциях на координатную ось: ( mg-N=-ma ) или ( N=mg+ma ). Поскольку ( N=P ), ( P=m(g+a) ).
Таким образом, если тело движется вверх вместе с опорой или подвесом с ускорением, направленным противоположно ускорению свободного падения, то его вес больше силы тяжести, т.е. больше веса покоящегося тела. Увеличение веса тела при движении с ускорением называют перегрузкой. Перегрузки испытывают космонавт в космическом корабле, пилот реактивного самолёта при взлёте и посадке.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Имеются две абсолютно упругие пружины. Под действием одной и той же силы первая пружина удлинилась на 8 см, а вторая — на 4 см. Сравните жёсткость ( k_2 ) второй пружины с жёсткостью ( k_1 ) первой пружины.
1) ( k_1=k_2 )
2) ( 4k_1=k_2 )
3) ( 2k_1=k_2 )
4) ( k_1=2k_2 )
2. Имеются две абсолютно упругие пружины: одна жёсткостью 200 Н/м, другая жёсткостью 400 Н/м. Сравните силу упругости ( F_2 ), возникающую во второй пружине, с силой упругости ( F_1 ), возникающей в первой пружине, при одинаковом их удлинении.
1) ( F_2=F_1 )
2) ( F_2=4F_1 )
3) ( 2F_2=F_1 )
4) ( 0.5F_2=F_1 )
3. Ученик, растягивая пружину динамометра последовательно на 1Н, 2Н, ЗН и 4Н, каждый раз измерял её удлинение и результаты измерений вносил в таблицу. Определите по данным таблицы жёсткость пружины динамометра.
1) 0,02 Н/м
2) 0,5 Н/м
3) 2 Н/м
4) 50 Н/м
4. На рисунке приведены графики зависимости силы упругости от удлинения. Сравните жёсткость пружин.
1) ( k_2=k_1 )
2) ( k_2>k_1 )
3) ( k_2<k_1 )
4) ( k_2geq k_1 )
5. Учащийся выполнял эксперимент по измерению удлинения ( x ) пружин при подвешивании к ним грузов. Полученные учащимся результаты представлены на рисунке в виде диаграммы. Какой вывод о жёсткости пружин ( k_1 ) и ( k_2 ) можно сделать из анализа диаграммы, если к концам пружин были подвешены грузы одинаковой массы?
1) ( k_2=4k_1 )
2) ( k_1=2k_2 )
3) ( k_2=2k_1 )
4) ( k_1=k_2 )
6. Под действием силы 3 Н пружина удлинилась на 4 см. Чему равна сила, под действием которой удлинение этой пружины составит 6 см?
1) 3,5 Н
2) 4 Н
3) 4,5 Н
4) 5 Н
7. Две пружины растягиваются одинаковыми силами. Жёсткость первой пружины ( k_1 ) в 2 раза больше жесткости второй пружины ( k_2 ). Удлинение первой пружины ( Delta l_1 ), удлинение второй пружины ( Delta l_2 ) равно
1) ( 0.5Delta l_1 )
2) ( 0.67Delta l_1 )
3) ( 1.5Delta l_1 )
4) ( 2.5Delta l_1 )
8. В лифте, движущемся вниз равноускоренно из состояния покоя, стоит ящик. Модуль веса ящика
1) равен модулю силы тяжести
2) больше модуля силы тяжести
3) меньше модуля силы тяжести
4) увеличивается с увеличением скорости лифта
9. Человек испытывает перегрузки при
1) равномерном движении вниз
2) равномерном движении вверх
3) равноускоренном движении вверх из состояния покоя
4) равноускоренном движении вниз с ускорением свободного падения
10. Различие веса тела на экваторе и на полюсе можно обнаружить
А. Взвешивая тело на рычажных весах
Б. Взвешивая тело на пружинных весах
Правильный ответ
1)только А
2)только Б
3) и А, и Б
4) ни А, ни Б
11. Установите соответствие между физической величиной (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Модуль силы упругости пружины
Б. Жёсткость пружины
B. Модуль удлинения пружины
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) уменьшается
2) увеличивается
3) не изменяется
12. Из приведённых ниже высказываний выберите два верных и запишите их номера в таблицу.
1) Закон Гука справедлив при любых деформациях.
2) Сила упругости направлена в сторону, противоположную деформации.
3) Жёсткость зависит только от материала, из которого изготовлено тело.
4) Вес тела всегда равен действующей на него силе тяжести.
5) Вес приложен к опоре или к подвесу.
Часть 2
13. Груз массой 5 кг начинают поднимать вертикально вверх с ускорением 2 м/с2. Чему равен вес груза?
Ответы
Сила упругости. Вес тела
3 (60%) 6 votes
Источник
