Гипотеза плоского сечения для растяжения
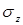
Гипотезу плоских сечений при изгибе можно объяснить на примере: нанесем на боковой поверхности недеформированной балки сетку, состоящую из продольных и поперечных (перпендикулярных к оси) прямых линий. В результате изгиба балки продольные линии примут криволинейное очертание, а поперечные практически останутся прямыми и перпендикулярными к изогнутой оси балки.
Формулировка гипотезы плоских сечения: поперечные сечения, плоские и перпендикулярные к оси балки до деформации, остаются плоскими и перпендикулярными к изогнутой оси после ее деформации.
Это обстоятельство свидетельствует: при изгибе выполняется гипотеза плоских сечений, как при растяжении и кручении
Помимо гипотезы плоских сечений принимается допущение: продольные волокна балки при ее изгибе не надавливают друг на друга.
Гипотезу плоских сечений и допущение называют гипотезой Бернулли.
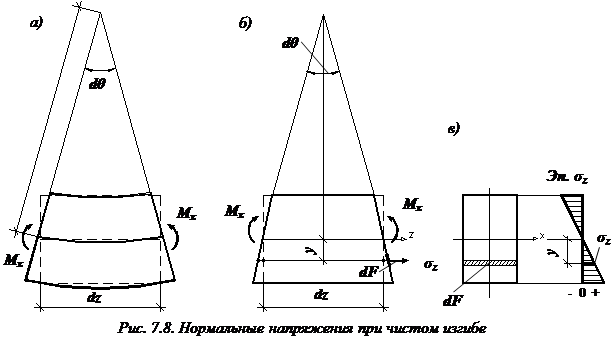
Рассмотрим балку прямоугольного поперечного сечения, испытывающую чистый изгиб (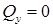
). Выделим элемент балки длиной 
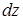(рис. 7.8. а). В результате изгиба поперечные сечения балки повернутся, образовав угол 
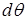. Верхние волокна испытывают сжатие, а нижние растяжение. Радиус кривизны нейтрального волокна обозначим 
.
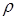Условно считаем, что волокна изменяют свою длину, оставаясь при этом прямыми (рис. 7.8. б). Тогда абсолютное и относительное удлинения волокна, отстоящего на расстоянии y от нейтрального волокна:
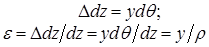
По закону Гука:
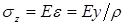
Покажем, что продольные волокна, не испытывающие при изгибе балки ни растяжения, ни сжатия, проходят через главную центральную ось x.
Поскольку длина балки при изгибе не изменяется, продольное усилие (N), возникающее в поперечном сечении, должно равняться нулю. Элементарное продольное усилие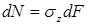 
.
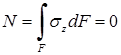
С учетом выражения :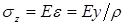
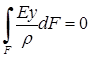
Множитель 
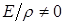можно вынести за знак интеграла (не зависит от переменной интегрирования).
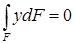
Выражение представляет статический момент инерции поперечного сечения балки относительно нейтральной оси x. Он равен нулю, когда нейтральная ось проходит через центр тяжести поперечного сечения. Следовательно, нейтральная ось (нулевая линия) при изгибе балки проходит через центр тяжести поперечного сечения.
Очевидно: изгибающий момент связан с нормальными напряжениями, возникающими в точках поперечного сечения стержня. Элементарный изгибающий момент, создаваемый элементарной силой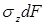 
:
,
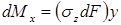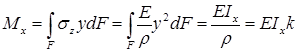
где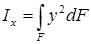 
– осевой момент инерции поперечного сечения относительно нейтральной оси x, а отношение 
— кривизна оси балки.
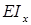— жесткость балки при изгибе (чем больше, тем меньше радиус кривизны ).
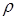Полученная формула 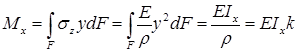представляет собой закон Гука при изгибе для стержня: изгибающий момент, возникающий в поперечном сечении, пропорционален кривизне оси балки.
Выражая из формулы закона Гука для стержня при изгибе радиус кривизны (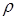) и подставляя его значение в формулу 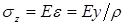, получим формулу для нормальных напряжений (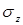) в произвольной точке поперечного сечения балки, отстоящей на расстоянии y от нейтральной оси x: 
.
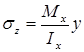В формулу для нормальных напряжений (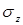) в произвольной точке поперечного сечения балки следует подставлять абсолютные значения изгибающего момента (
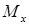) и расстояния от точки до нейтральной оси (координаты y). Будет ли напряжение в данной точке растягивающим или сжимающим легко установить по характеру деформации балки или по эпюре изгибающих моментов, ординаты которой откладываются со стороны сжатых волокон балки.
Из формулы 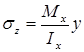видно: нормальные напряжения (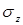) изменяются по высоте поперечного сечения балки по линейному закону. На рис. 7.8, в показана эпюра нормальных напряжений. Наибольшие напряжения при изгибе балки возникают в точках, наиболее удаленных от нейтральной оси. Если в поперечном сечении балки провести линию, параллельную нейтральной оси x, то во всех ее точках возникают одинаковые нормальные напряжения.
Несложный анализ эпюры нормальных напряжений показывает, при изгибе балки материал, расположенный вблизи нейтральной оси, практически не работает. Поэтому в целях снижения веса балки рекомендуется выбирать такие формы поперечного сечения, у которых большая часть материала удалена от нейтральной оси, как, например, у двутаврового профиля.
Источник
ГЛАВА 8. ИЗГИБ СТЕРЖНЕЙ
29. Гипотеза плоских сечений и нормальные напряжения изгиба
Силовые факторы в сечении стержня.
Рассмотрим стержень (крыло самолета, лопатку компрессора и т. д.) под действием поперечной нагрузки (рис. 8.1). Ось z направлена вдоль оси стержня, оси х, у лежат в плоскости А поперечного сечения.
Проведем сечение (см. рис. 8.1) и заменим отброшенную правую часть тела равнодействующими внутренних сил (рис. 8.2).
Рис. 8.1. Лопатка компрессора под действием изгибающей нагрузки
Рис. 8.2. Силовые факторы в сечении стержня
В общем случае для равновесия оставленной части тела необходимо и достаточно приложить три составляющие вектора усилия и три составляющие вектора момента. Векторы Q и называются поперечными или перерезывающими силами; N — продольная или нормальная сила; моменты М и называются изгибающими моментами; — крутящий момент (см. рис. 8.2).
В пределах упругости материала кручение можно рассматривать независимо от других деформаций; оно было описано ранее, и потому в дальнейшем считаем
Положительные направления изгибающих моментов соответствуют положительным направлениям вращения, принятым для правосторонней системы координат. Согласно этому, момент или вращение считается положительным в том случае, когда поворот осуществляется против часовой стрелки, если смотреть со стороны положительного направления оси к началу координат (рис. 8.2). Усилия будем считать положительными, если они направлены вдоль осей х и у соответственно (см. рис. 8.2) .
Замечание. В приведенном соглашении о знаках силовых факторов существенно, что рассматриваются усилия, действующие на левую часть стержня (нормаль к сечению идет в положительном направлении оси z). В силу равенства действия и противодействия в таком же сечении, но принадлежащем правой части стержня (рис. 8.3), силы и моменты будут точно такими же, но противоположно направленными. Естественно, что для правой части стержня (внешняя нормаль к сечению направлена вдоль отрицательного направления оси z) положительные направления будут противоположными.
Рис. 8.3. Силовые факторы, приложенные к левой и правой частям стержня: а — положительные силовые факторы в сечении стержня; б — правило знаков для перерезывающей силы и изгибающего момента
Подобное обстоятельство встречалось, ранее (разд. 3) при установлении знаков напряжений.
Таким образом, правило знаков зависит от направления внешней нормали к сечению и принятой системы координат. На рис. 8.3 показаны положительные силовые факторы в сечении стержня.
Гипотеза плоских сечений.
Точное решение задачи о распределении нормальных и касательных напряжений при изгибе стержня представляет большие трудности.
В инженерной практике нашло широкое признание приближенное решение, основанное на знаменитой «гипотезе плоских сечений», впервые использованной (в простейших случаях) еще в работах Бернулли и Эйлера.
Рис. 8.4. Распределение упругого смещения в поперечном сечении стержня при изгибе
Гипотеза плоских сечений состоит в следующем: точки плоскости поперечного сечения после деформации лежат в одной плоскости. Физически это означает, что сечение стержня можно представить как тонкую, абсолютно жесткую пластинку, получающую в результате деформации стержня линейное смещение и углы поворота. Перемещение точки А поперечного сечения (рис. 8.4) вдоль оси z по гипотезе плоских сечений будет таким:
где — углы поворота сечения относительно осей х и у соответственно, — смещение вдоль оси z точек оси стержня.
Величины одинаковы для всех точек сечения, но в общем случае зависят от z. Углы упругого поворота сечения в формуле (1) считаются малыми, так что
Замечание. Гипотеза плоских сечений является важнейшим приближенным методом описания деформации изгиба и растяжения стержней. Исследования показывают, что основой гипотезы плоских сечений является предположение о малости углов сдвига элементов по сравнению с углами их поворотов.
При изгибестержней из адизотроппых материалов, у которых модуль сдвига может быть на порядок величины меньше модуля упругости при растяжении, деформации сдвига возрастают и область применения гипотезы плоских сечений становится ограниченной.
Источник
Макеты страниц
Ставя своей задачей определение только нормальных напряжений изгиба, в основу теории достаточно положить гипотезу о том, что плоские до деформации поперечные сечения балки остаются после деформации плоскими и перпендикулярными деформированной оси. Теория изгиба, построенная на гипотезе плоских сеченнй, была в основном завершена уже Л. Эйлером и носит название теории Бернулли — Эйлера или технической теории изгиба. Точная теория изгиба, построенная Сен-Венаном для того случая, когда балка загружена сосредоточенными силами, а также немногочисленные строгие решения задачи об изгибе распределенной нагрузкой приводят к заключению, что, хотя гипотеза Бернулли не вполне верна, все же основанные на ней расчеты оказываются весьма точными.
Рис. 147.
Гипотеза плоских сечений позволяет составить представление о характере деформированного состояния стержня. Рассмотрим два бесконечно близких сечения балки на расстоянии одно от другого (рис. 147). Попытаемся определить деформацию элемента параллельного оси и заключенного между двумя сечениями; длина его есть Поместим оси координат х и у в плоскости левого сечения, координаты точки суть х, у, 0; точки — суть . Будем изучать перемещение правого сечения относительно левого, считая последнее неподвижным. Деформация изгиба заключается в том, что правое сечение, во-первых, перемещается вдоль оси z на величину , во-вторых, поворачивается относительно оси х на угол и, наконец, поворачивается около оси у на угол .
Вследствие параллельного перемещения сечения отрезок получает удлинение следовательно, относительное удлинение его есть .
Вследствие поворота около оси х точка переместится на длину значит, относительное удлинение отрезка будет . Аналогично находим, что от поворота вокруг оси у удлинение есть . Полное удлинение отрезка есть
(102.1)
Легко видеть, что суть кривизны проекций изогнутой оси на координатные плоскости.
В теории изгиба употребляют термин «волокно», уподобляя сплошное вещество, из которого сделан стержень, веществу волокнистой структуры типа дерева. Нужно помнить, что такое уподобление неправильно. Мы будем называть волокном материальную линию, бывшую до деформации прямой, параллельной оси стержня. Координаты х и у точки пересечения волокна с плоскостью любого поперечного сечения назовем координатами волокна. Таким образом, уравнение (102.1) показывает, что удлинение волокна есть линейная функция его координат.
Рис. 148.
Для перехода к напряжениям важно отметить, что напряженное состояние волокна является состоянием простого растяжения; в плоскостях, параллельных оси стержня, нормальные напряжения отсутствуют. Последнее нужно понимать только в том смысле, что эти напряжения весьма малы по сравнению с остальными напряжениями изгиба. Действительно, обратимся к рис. 148, на котором изображена балка квадратного сечения со стороной b и длиной загруженная распределенным по верхней плоскости давлением . Вся сила, действующая на балку, есть
Пользуясь оценкой для , найдем:
Рассечем балку горизонтальной плоскостью. Очевидно, что в этой плоскости будут действовать нормальные напряжения о причем если плоскость близка к верхней граничной плоскости, то о весьма мало отличается от ; если плоскость сечения близка к нижней граничной плоскости, то мало отличается от нуля.
Поэтому
Сравнивая , видим, что очень мало по сравнению с . Если порядок малости касательных напряжений есть то порядок малости есть этим напряжением можно пренебрегать и подавно.
Итак, будем считать, что каждое волокно растягивается в продольном направлении, причем напряжение связано с законом Гука в его простейшей форме:
Из формулы (102.1) получаем:
(102.2)
Очевидно, рассуждения, приведшие нас к убеждению, что каждое волокно можно считать находящимся в условиях простого растяжения, теряют силу тогда, когда к балке приложена сосредоточенная сила. Части балки, непосредственно примыкающие к месту приложения сосредоточенных сил, не могут рассчитываться по схеме плоских сечений: здесь возникают местные напряжения. Область, в которой отступления от закона плоских сечений существенны, невелика, длина ее имеет порядок поперечного размера. Для изгиба сохраняет силу принцип Сен-Венана, подробно освещенный в § 17 для растяжения-сжатия. Все сказанное там сохраняет силу и для изгиба.
Подчеркнем, что гипотеза плоских сечений и принцип Сен-Венана справедливы лишь для длинных стержней сплошного профиля, то есть имеющих поперечные размеры одного порядка. Для тонкостенных стержней, когда один поперечный размер значительно больше другого, оценки относительных порядков величин нормальных и касательных напряжений перестают быть справедливыми, гипотеза плоских сечений теряет силу и принцип Сен-Венана становится неприменимым.
Источник
Растяжением
(сжатием) называется такой вид деформации,
когда в поперечном сечении стержня под
действием внешних нагрузок возникает
только один внутренний силовой фактор
— продольная сила , а остальные внутренние
силовые факторы отсутствуют.
Продольная
сила вызывает нормальные напряжения,
определяемые:
—
при равномерном распределении их по
сечению
—
при неравномерном распределении
Продольная
сила и напряжение положительны при
растяжении и отрицательны при сжатии.
Принцип
Сен-Венана — в теории упругости —
положение, согласно которому уравновешенная
система сил, приложенная к некоторой
части твёрдого тела, вызывает в нём
появление неравномерности распределения
напряжений, которая быстро уменьшается
по мере удаления от этой части. На
расстояниях, больших максимального
линейного размера зоны приложения
нагрузок, неравномерность распределения
напряжения и деформации оказываются
пренебрежительно малыми. Сформулирован
Сен-Венаном в 1855 году. Строгого
доказательства этого принципа для
общего случая нет, однако он подтверждается
экспериментом, численными методами
решения задач и строгими аналитическими
решениями частных случаев.
Гипотеза
плоских сечений была установлена
Я. Бернулли в результате экспериментов:
при растяжении стержня продольные и
поперечные риски, нанесенные на его
поверхности до деформации, остаются
прямолинейными и взаимно перпендикулярными,
изменяются лишь расстояния между ними
(между поперечными рисками они
увеличиваются, а между продольными –
уменьшаются).
В
основе гипотезы плоских сечений лежит
предположение, что и внутри стержня
деформации имеют такой же характер, как
на поверхности. Следовательно, сечения,
плоские и нормальные к оси стержня до
деформации, остаются плоскими и
нормальными к его оси и после деформации.
В этом и заключается смысл гипотезы
плоских сечений.
Вопрос 6
Напряжение
при растяжении и сжатии
Принято
считать, что внутренние силы действуют
непрерывно по всему сечению. Мерой их
интенсивности является напряжение —
величина внутренних сил, приходящихся
на единицу площади сечения. Напряжение
представляет собой отношение
внутренней силы к некоторой площади
и измеряется в единицах силы, отнесенных
к единице площади: 1 H/м2 = 1Па.
Через
одну и ту же точку тела можно провести
бесчисленное множество сечений,
разделяющих тело на две части. В общем
случае напряжения по различным сечениям
будут различны.
Напряжения
в некоторой точке какого-либо сечения
тела характеризуются числовым значением
и направлением, т.е. напряжение представляет
собой вектор, наклоненный под тем или
иным углом к рассматриваемому сечению.
Направление и числовая величина
напряжения зависят от характера и
величины внешних сил, приложенных к
телу, от положения сечения в теле и
положения точки в сечении.
При
растяжении и сжатии в сечении действует
только нормальное
напряжение (нормаль к сечению).
Напряжения
в поперечных сечениях могут рассматриваться
как силы, приходящиеся на единицу
площади.
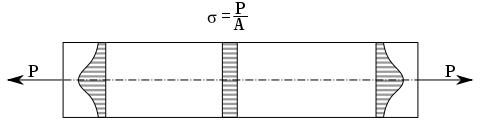
Таким образом, направление
и знак напряжения в сечении совпадают
с направлением и знаком силы в сечении
(рис.32.).
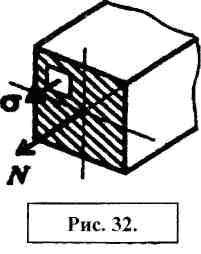
Исходя
из гипотезы плоских сечений, можно
предположить, что напряжение при
растяжении и сжатии в пределах каждого
сечения не меняются. Поэтому напряжение
можно рассчитать по формуле: где Nz
зх-продольная сила; А — площадь поперечного
сечения. Величина напряжения прямо
пропорциональна продольной силе и
обратно пропорциональна площади
поперечного сечения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
· Гипотеза плоских сечений предполагает, что все сечения элемента остаются плоскими при деформировании. Если линия действия внешней силы строго совпадает с продольной осью бруса, то в его поперечном сечении возникает единственный силовой фактор — продольная сила .Гипотеза плоск. сеч.при центральном растяжении или сжатии плоские поперечные сечения бруса в процессе его деформации сохраняются плоскими, и лишь перемещаются параллельно самим себе.
Что называется напряжением? На какие составляющие принято раскладывать полное напряжение в точке сечения? Как они называются?
· Напряжение – это векторная величина, кот. характеризует интенсивность распределения внутренних сил в поперечном сечении тела.
При уменьшении размеров площадки соответственно уменьшаются главный вектор и главный момент внутренних сил, причем главный момент уменьшается в большей степени. В пределе при получим полное напряжение в точке:
Вектор полного напряжения раскладывается как правило по 3 – м взаимно перпендик. направлениям: нормальное напряжение проекция вектора полного напряжения на нормаль к сечению, касательное напряжение – проекция вектора полного напряжения на ось, лежащую в плоскости сечения.
Какие напряжения возникают в поперечном сечении стержня при растяжении-сжатии? Как вычисляются эти напряжения? Как они направлены?
· в попер. сечении д – т нормальные напряжения σ=N/A. На наклонной площадке полные напряжения рα = направлены вдоль продольной оси и распределены равномерно=σ cos α. Это полное напряжение разложим на нормальное и касательное: σα =рα cos α= σ cos α cos α = σ cos2 α ,
τα= рα sin α= σ cos α sin α=σ/2 sin 2α.
-на площадках, совпадающих с поперечным сечением при α=0, σα= σmax=σz=N/A, τα=0,
-на площ., наклоненных под углом 450: σα= σz/2= N/A, τα= τmax= σz/2
-на продольных площ.(при α=900) : σα= τα=0.
По каким сечениям действуют максимальные нормальные и касательные напряжения при растяжении-сжатии?
· -на площадках, совпадающих с поперечным сечением при α=0, σα= σmax=σz=N/A, -на площ., наклоненных под углом 450: τα= τmax= σz/2
Что называют пределом пропорциональности, пределом упругости, пределом текучести, пределом прочности (временным сопротивлением)?
· Предел пропорциональности – условное напряжение до которого наблюдается линейная зависимость м/напряж. и деформацией (м/силой и удлинением) – з. Гука.
Предел упругости –такое наибольшее напряжение, до кот. материал не получает остаточных деформаций.
Предел текучести – усл. напряжение при кот. происходит рост деформации при постоянном напряжении.
Предел прочности – усл. напряжение, соответствующее максимальной нагрузке.
7. Изобразить примерный вид диаграммы растяжения образца из мягкой стали, показать характерные зоны на этой диаграмме.
· О1-зона упругости, 2С-зона общей текучести, С3 – зона упрочнения, 34 – зона местной текучести.
Какие свойства материала характеризуют относительное остаточное удлинение и относительное остаточное сужение в месте разрыва?
· относительное остаточное удлинение : , относительное остаточное сужение: характеризуют пластические свойства материалов.
Какие величины характеризуют степень пластичности материала.
- относительное остаточное сужение, относительное остаточное удлинение.
10.Что называется «наклепом» и как он используется в технике?
· Наклеп – повышение упругих св-в материала за счет предварительного нагружения стержня за зону текучести, с последующей разгрузкой. Такой обработке подвергаются некоторые виды арматуры, цепи и канаты подьемных машин(чтобы устранить остаточные удлинения).
Чему равна работа затраченная на разрыв образца?
· Площадь, заключенная под первичной диаграммой растяжения , численно равна работе, затраченной на разрушение образца.
Чему равна работа затраченная на упругую деформацию после разрыва образца?
· площадь треугольника О1перп.
13. Как определить работу, затраченную на пластическую деформацию
после разрыва образца?
· площадь фигуры О3перп.???
Как по диаграмме растяжения определить абсолютное остаточное
Источник