Формула закона гука на растяжение
Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука (1635— 1703).
Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению. Математически закон Гука можно записать в виде равенства
Коэффициент пропорциональности Е характеризует жесткость материала, то есть его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода.
Модуль упругости и напряжение выражаются в одинаковых единицах: [Е = [ст]/[е] = Па.
В таблице 2.1 приведены значения ?для некоторых материалов.
Таблица 2.1
Материал | Е, МПа |
Чугун | (1,5…1,6) ТО5 |
Сталь | (1,96…2,16) ТО5 |
Медь | (1,0…1,3)105 |
Сплавы алюминия | (0,69…0,71) ТО5 |
Дерево (вдоль волокон) | (0,1—.0,16) -105 |
Текстолит | (0,06…0,1)-105 |
Капрон | (0,01…0,02) ТО5 |
Если в формулу закона Гука подставим выражения а = N/A, е = А///, то получим
Произведение ЕЛ, стоящее в знаменателе, называется жесткостью сечения при растяжении и сжатии; оно характеризует одновременно физикомеханические свойства материала и геометрические размеры поперечного сечения бруса. Соответственно, данная формула читается так: абсолютное удлинение или укорочение прямо пропорционально продольной силе и длине и обратно пропорционально жесткости сечения бруса.
Приведенные выше формулы закона Гука применимы только для брусьев или их участков постоянного поперечного сечения, изготовленных из одного материала и при постоянной продольной силе.
Для бруса, имеющего несколько участков, отличающихся материалом, размерами поперечного сечения, продольной силой, изменение длины всего бруса равно алгебраической сумме удлинений и укорочений отдельных участков:
Пример 2.2
На стальной ступенчатый брус действуют силы F= 40 кН и R = 60 кН. Площади поперечных сечений равны Ах = 800 мм2, Л2 = 1600 мм2. Длины участков указаны на рис. 2.4; а = 0,2 м. Определить изменение длины бруса двумя способами:
- 1) с помощью эпюры продольных сил;
- 2) с помощью принципа независимости действия сил.
Принять Е= 2-1011 Па.
Рис. 2.4
Решение.
1-й способ. Разобьем брус на участки и применяя метод сечений, определим значения продольных сил на каждом из них: Nx — N2 — —40 кН (сжатие), N3 = 20 кН (растяжение). Строим эпюру продольных сил.
Для бруса, состоящего из нескольких участков, А/ = A/i + Д/2 +Д/з, где по закону Гука
. Изменение длины первого участка
; аналогично
— изменения длин второго и третьего участков.
Следовательно,
Подставив числовые значения с учетом знаков продольных сил, получим
Произведя вычисления, получим Д/= —0,15 — 0,025 + 0,025 = —0,15 мм.
Следовательно, брус укоротится на 0,15 мм.
2-й способ. Применим принцип независимости действия сил. Изменение длины бруса Д/ будет складываться из укорочения AlF всего бруса под действием силы F и удлинения ДlR третьего участка под действием силы R: Д/ = AlF + + AlR. Вычислим каждое из этих слагаемых.
А1Р = -F- 3а/{ЕА) — F(a + 2а)/(ЕА2)’, подставляя числовые значения, получим А1Р= —0,225 мм.
Аналогично находим AlR = R ?2а/{ЕА2); AlR = 0,075 мм.
Отсюда Д/ — —0,225 + 0,075 = —0,15 мм.
Решая задачу двумя способами, мы получили один и тот же результат, что свидетельствует о правильности решения.
Источник
Закон Гука был открыт в XVII веке англичанином Робертом Гуком. Это открытие о растяжении пружины является одним из законов теории упругости и выполняет важную роль в науке и технике.

Определение и формула закона Гука
Формулировка этого закона выглядит следующим образом: сила упругости, которая появляется в момент деформации тела, пропорциональна удлинению тела и направлена противоположно движению частиц этого тела относительно других частиц при деформации.
Математическая запись закона выглядит так:
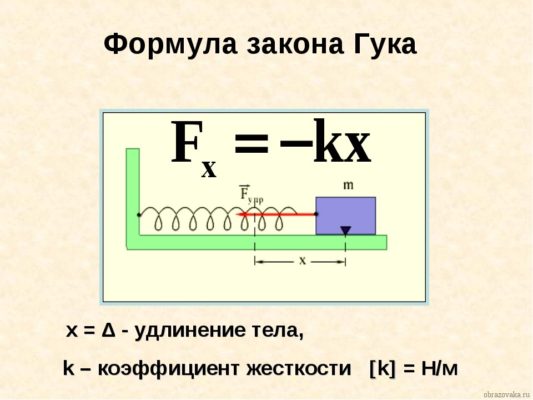
Рис. 1. Формула закона Гука
где Fупр – соответственно сила упругости, x – удлинение тела (расстояние, на которое изменяется исходная длина тела), а k – коэффициент пропорциональности, называемый жесткостью тела. Сила измеряется в Ньютонах, а удлинение тела – в метрах.
Для раскрытия физического смысла жесткости, нужно в формулу для закона Гука подставить единицу, в которой измеряется удлинение – 1 м, заранее получив выражение для k.
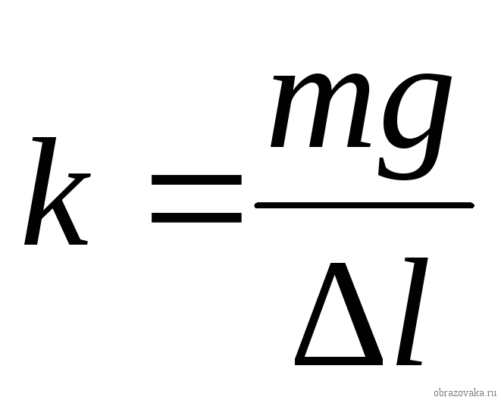
Рис. 2. Формула жесткости тела
Эта формула показывает, что жесткость тела численно равна силе упругости, которая возникает в теле (пружине), когда оно деформируется на 1 м. Известно, что жесткость пружины зависит от ее формы, размера и материала, из которого произведено данное тело.
Сила упругости
Теперь, когда известно, какая формула выражает закон Гука, необходимо разобраться в его основной величине. Основной величиной является сила упругости. Она появляется в определенный момент, когда тело начинает деформироваться, например, когда пружина сжимается или растягивается. Она направлена в обратную сторону от силы тяжести. Когда сила упругости и сила тяжести, действующие на тело, становятся равными, опора и тело останавливаются.
Деформация – это необратимые изменения, происходящие с размерами тела и его формой. Они связанны с перемещением частиц относительно друг друга. Если человек сядет в мягкое кресло, то с креслом произойдет деформация, то есть изменятся его характеристики. Она бывает разных типов: изгиб, растяжение, сжатие, сдвиг, кручение.
Так как сила упругости относится по своему происхождению к электромагнитным силам, следует знать, что возникает она из-за того, что молекулы и атомы – наименьшие частицы, из которых состоят все тела, притягиваются друг другу и отталкиваются друг от друга. Если расстояние между частицами очень мало, значит, на них влияет сила отталкивания. Если же это расстояние увеличить, то на них будет действовать сила притяжения. Таким образом, разность сил притяжения и сил отталкивания проявляется в силах упругости.
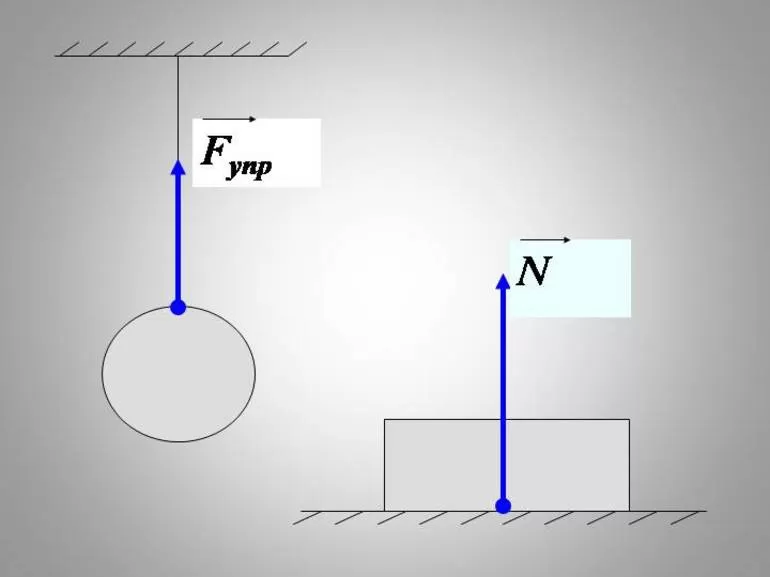
Сила упругости включает в себя силу реакции опоры и вес тела. Сила реакции представляет особый интерес. Это такая сила, которая действует на тело, когда его кладут на какую-либо поверхность. Если же тело подвешено, то силу, действующую на него, называют, силой натяжения нити.
Особенности сил упругости
Как мы уже выяснили, сила упругости возникает при деформации, и направлена она на восстановление первоначальных форм и размеров строго перпендикулярно к деформируемой поверхности. У сил упругости также есть ряд особенностей.
- они возникают во время деформации;
- они появляются у двух деформируемых тел одновременно;
- они находятся перпендикулярно поверхности, по отношению к которой тело деформируется.
- они противоположны по направлению смещению частиц тела.
Применение закона на практике
Закон Гука применяется как в технических и высокотехнологичных устройствах, так и в самой природе. Например, силы упругости встречаются в часовых механизмах, в амортизаторах на транспорте, в канатах, резинках и даже в человеческих костях. Принцип закона Гука лежит в основе динамометра – прибора, с помощью которого измеряют силу.

Рис. 3. Динамометр
Что мы узнали?
Статья подробно знакомит учащихся с материалом о том, как формулируется обобщенный закон Гука, который изучают в 7 классе, и его основной величине – силе упругости.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Тимур Катаев
10/10
Влад Демченко
7/10
Александр Коновалов
10/10
Октябрина Баева
10/10
Киара Кольт
8/10
Алина Фесова
9/10
Яніна Резніченко
8/10
Артемий Здор
8/10
Александра Щербина
9/10
Катя Пу
10/10
Оценка доклада
Средняя оценка: 4.3. Всего получено оценок: 583.
Источник
Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие
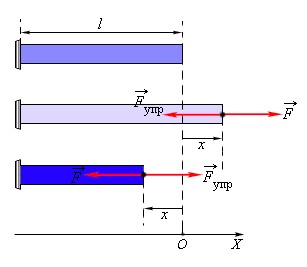
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Закон Гука
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k — коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
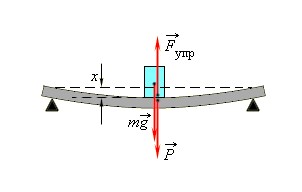
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр.
Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.
Источник
Физика, 10 класс
Урок 9. Закон Гука
Перечень вопросов, рассматриваемых на этом уроке
1.Закона Гука.
2.Модели видов деформаций.
3. Вычисление и измерение силы упругости, жёсткости и удлинение пружины.
Глоссарий по теме
Сила упругости – это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.
Деформация – изменение формы или размеров тела, происходящее из-за неодинакового смещения различных частей одного и того же тела в результате воздействия другого тела. Виды деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
Закон Гука – сила упругости, возникающая при деформации тела (растяжение или сжатие пружины), пропорциональна удлинению тела (пружины), и направлена в сторону противоположную направлению перемещений частиц тела
Основная и дополнительная литература по теме:
Г.Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр. 107-112
Рымкевич А.П. Сборник задач по физике. 10-11класс.- М.:Дрофа,2009. Стр 28-29
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Основное содержание урока
В окружающем нас мире мы наблюдаем, как различные силы заставляют тела двигаться, делать прыжки, перемещаться, взаимодействовать.
Однако можно также наблюдать как происходят разрушения, так называемые деформации, различных сооружений: мостов, домов, разнообразных машин.
Что необходимо знать инженеру конструктору, строителю, чтобы строить надёжные сооружения: дома, мосты, машины?
Почему деформации различны, какие виды деформации могут быть у конкретных тел? Почему одни тела после деформации могут восстановиться, а другие нет? От чего зависит и можно ли рассчитать величину этих деформаций?
Деформация — это изменение формы или размеров тела, в результате воздействия на него другого тела.
Почему деформации не одинаковы у различных тел, если мы их, к примеру, сжимаем? Давайте вспомним что мы знаем о строении вещества.
Все вещества состоят из частиц. Между этими частицами существуют силы взаимодействия- эти силы электромагнитной природы. Эти силы в зависимости от расстояний между частицами проявляются, то как силы притяжения, то как силы отталкивания.
Сила упругости – сила, возникающая при деформации любых тел, а также при сжатии жидкостей и газов. Она противодействует изменению формы тел.
Мы можем наблюдать несколько видов деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
При деформации растяжения межмолекулярные расстояния увеличиваются. Такую деформацию испытывают струны в музыкальных инструментах, различные нити, тросы, буксирные тросы.
При деформации сжатия межмолекулярные расстояния уменьшаются. Под такой деформацией находятся стены, фундаменты сооружений и зданий.
При деформации изгиба происходят неординарные изменения, одни межмолекулярные слои увеличиваются, а другие уменьшаются. Такие деформации испытывают перекрытия в зданиях и мостах.
При кручении – происходят повороты одних молекулярных слоёв относительно других. Эту деформацию испытывают: валы, витки цилиндрических пружин, столярный бур, свёрла по металлу, валы при бурении нефтяных скважин. Деформация среза тоже является разновидностью деформации сдвига.
Первое научное исследование упругого растяжения и сжатия вещества провёл английский учёный Роберт Гук.
Роберт Гук установил, что при малых деформациях растяжения или сжатия тела абсолютное удлинение тела прямо пропорционально деформирующей силе.
F упр = k ·Δℓ = k · Iℓ−ℓ0I закон Гука.
k− коэффициент пропорциональности, жёсткость тела.
ℓ0 — начальная длина.
ℓ — конечная длина после деформации.
Δℓ = I ℓ−ℓ₀ I- абсолютное удлинение пружины.
— единица измерения жёсткости в системе СИ.
При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе, а слишком большие деформации разрушают тело.
Для расчёта движения тел под действием силы упругости, нужно учитывать направление этой силы. Если принять за начало отсчёта крайнюю точку недеформированного тела, то абсолютное удлинение тела можно характеризовать конечной координатой деформированного тела. При растяжении и сжатии сила упругости направлена противоположно смещению его конца.
Закон Гука можно записать для проекции силы упругости на выбранную координатную ось в виде:
F упр x = − kx — закона Гука.
k – коэффициент пропорциональности, жёсткость тела.
x = Δℓ = ℓ−ℓ0 удлинение тела (пружины, резины, шнура, нити….)
Fупр x = − kx
Закон Гука:
Fупр = k·Δℓ = k · Iℓ−ℓ0I
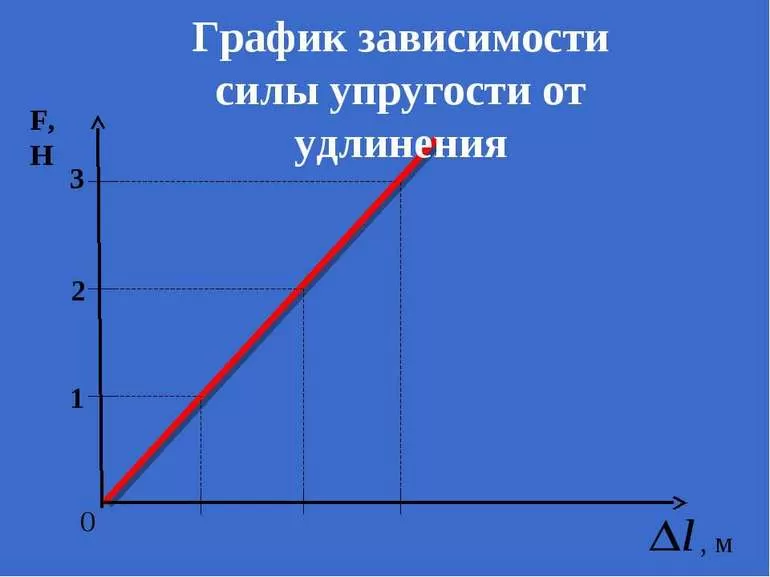
Графиком зависимости модуля силы упругости от абсолютного удлинения тела является прямая, угол наклона которой к оси абсцисс зависит от коэффициента жёсткости k. Если прямая идёт круче к оси силы упругости, то коэффициент жёсткости этого тела больше, если же уклон прямой идёт ближе к оси абсолютного удлинения, следует понимать, что жёсткость тела меньше.
График, зависимости проекции силы упругости на ось ОХ, того же тела от значения х.
Необходимо помнить, что закон Гука хорошо выполняется при только при малых деформациях. При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе.
Разбор тренировочных заданий
1. По результатам исследования построен график зависимости модуля силы упругости пружины от её деформации. Чему равна жёсткость пружины? Каким будет удлинение этой пружины при подвешивании груза массой 2кг?
Решение: По графику идёт линейная зависимость модуля силы упругости и удлинение пружины. Зависимость физических величин по Закону Гука:
F упр x = − kx (1)
Fупр =k·Δℓ = k · Iℓ−ℓ0I (2)
Из формулы (1) выражаем:
Зная что Fт = mg = 20 Н, Fт = Fупр= k·Δℓ следовательно
Ответ: жёсткость пружины равна 200 Н/м, удлинение пружины равно 0,1м.
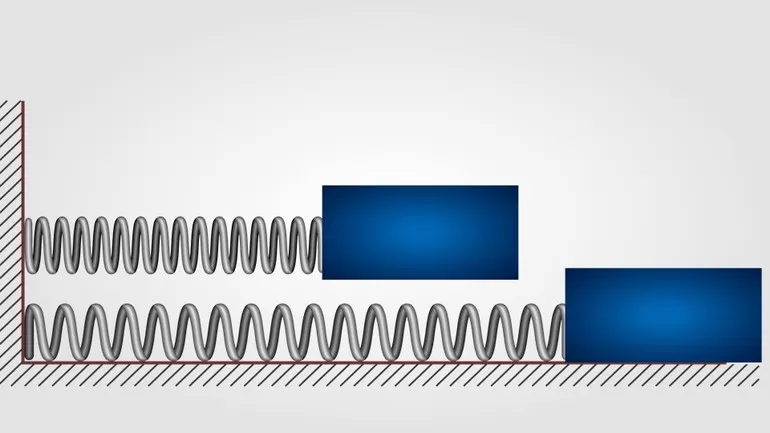
2. К системе из кубика массой 1 кг и двух пружин приложена постоянная горизонтальная сила. Система покоится. Между кубиком и опорой трения нет. Левый край первой пружины прикреплён к стенке. Удлинение первой пружины 0,05 м. Жёсткость первой пружины равна 200 Н/м. Удлинение второй пружины 0,25 м.
- Чему равна приложенная к системе сила?
- Чему равна жёсткость второй пружины?
- Во сколько раз жёсткость второй пружины меньше чем первой?
Решение:
1. По условию задачи система находится в покое. Зная жёсткость и удлинение пружины найдём силу, которая уравновешивает приложенную постоянную горизонтальную силу.
F = F упр =k1·Δℓ1= 200 Н/м·0,05 м = 10 Н
2. Жёсткость второй пружины:
3. k1/ k2 = 200/40 = 5
Ответ: F=10 Н; k2 = 40 Н/м; k1/k2 = 5.
Источник

Для проектирования таких механизмов требуется базовое понимание того, что из себя представляют упругость, кручение и сила, поэтому инженерам необходимо знать определение и формулу закона Гука.
Свойства пружины
Пружина — это объект, который может деформироваться под воздействием силы, а после того как сила будет устранена, вернётся к своей первоначальной форме. Пружины бывают самых разных форм и являются неотъемлемой частью практически всех умеренно сложных механических устройств: от шариковых ручек до двигателей гоночных автомобилей.
В самой форме спиральной пружины нет никаких особенностей. «Пружинность», или, точнее, эластичность, является фундаментальным свойством проволоки, из которой изготовлена пружина. Длинная прямая металлическая проволока также обладает способностью «отскакивать» после растяжения или скручивания.

Смотка проволоки в пружину позволяет использовать свойства длинного куска в небольшом пространстве. Это гораздо удобнее для сборки механических устройств.
Реакция металлической проволоки на растяжение (осевая нагрузка) и скручивание (кручение) определяется различными физическими свойствами, и в конструкции конкретной пружины один вид деформации может преобладать над другим.
Кроме того, упругие свойства металлов сильно зависят от микроструктуры их зёрен. Это может быть изменено как напряжением, так и контролируемым процессом нагрева и охлаждения, известным как отжиг.
Если металлическая проволока была сформирована из прямого сечения в катушку, то, вероятно, её необходимо будет повторно отжечь для восстановления первоначальных упругих свойств.
Принципы деформации
Когда сила воздействует на материал, он растягивается или сжимается в ответ. В механике сила, приложенная на единицу площади, является тем, что называется напряжением. Степень растяжения и сжатия, возникающая, когда материал реагирует на напряжение, называется деформацией. Напряжение измеряется отношением разницы в длине к исходной длине в направлении напряжения.
Каждый материал по-разному реагирует на стресс, и детали этой реакции важны для инженеров, выбирающих материалы для своих конструкций и машин, которые должны вести себя предсказуемо при ожидаемых напряжениях.
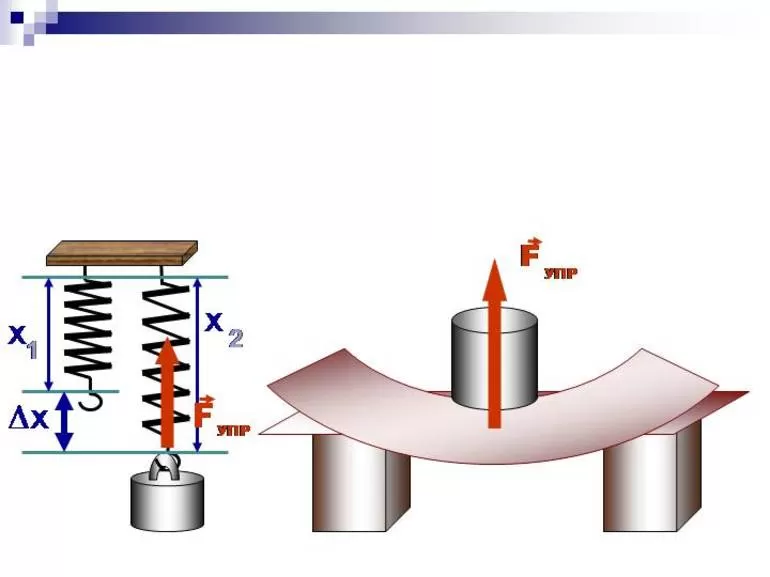
Для большинства материалов нагрузка, испытываемая при приложении небольшого напряжения, зависит от плотности химических связей. То же самое относится к жёсткости материала, которая напрямую связана с его химической структурой.
Происходящее при снятии напряжения зависит от того, насколько далеко перемещены атомы.
В целом существует два типа деформации:
- Упругая. После снятия напряжения материал возвращается к размеру, который был до приложения нагрузки. Деформация обратима, непостоянна.
- Пластическая. Напряжение настолько велико, что при снятии нагрузки материал не возвращается к своему предыдущему размеру. Минимальное значение напряжения, вызывающего пластическую деформацию, известно как предел упругости материала.
Любая пружина должна быть спроектирована точно таким образом, чтобы она испытывала только упругую деформацию при установке в машину при нормальной эксплуатации.
Суть закона
Закон назван в честь британского физика XVII века Роберта Гука, который впервые сформулировал его в 1676 году в виде анаграммы на латинском.
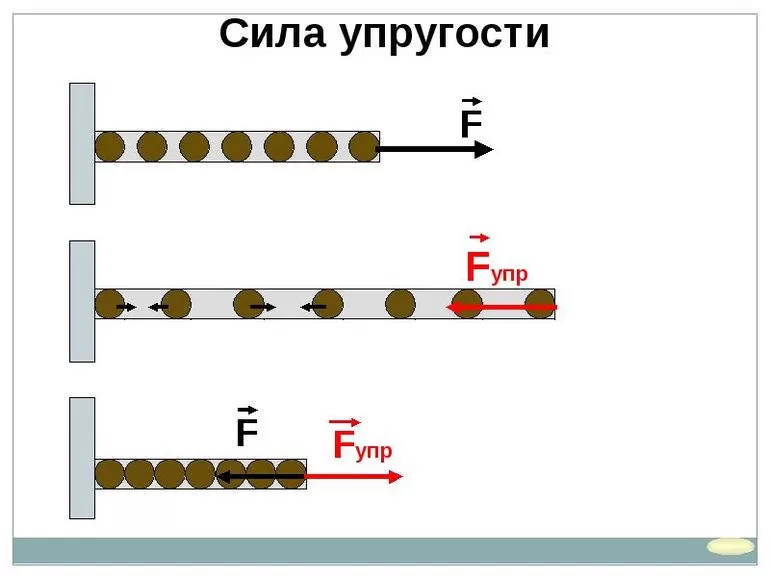
Он опубликовал её решение в 1678 году, утверждая, что открыл закон уже в 1660 году.
При изучении пружин и свойств их упругости, имеющих электромагнитную природу, физик отметил, что кривая зависимости напряжения от деформации для многих материалов имеет линейную область.
Вот как формулируется закон Гука: сила упругости, необходимая для растяжения упругого объекта, такого как металлическая пружина, равна или прямо пропорциональна удлинению пружины.
Эта формулировка математически записывается как F = -kx, где обозначения расшифровываются следующим образом:
- X — это смещение конца пружины от её положения равновесия.
- F — восстанавливающая сила, прилагаемая пружиной к этому концу.
- K — константа пропорциональности, известная как пружинная постоянная, которая обычно измеряется в N/m (ньютон метр).
Несколько пружин могут воздействовать на одну и ту же точку. В таком случае закон всё ещё может применяться. Как и с любым другим набором сил, силы многих пружин могут быть объединены в одну.
Когда действует закон Гука, поведение линейно. Если оно показано на графике или рисунке, линия, изображающая силу как функцию смещения, должна показывать прямое изменение. В правой части уравнения есть отрицательный знак, потому что восстанавливающая сила, создаваемая пружиной, находится в направлении, противоположном силе, вызвавшей смещение.
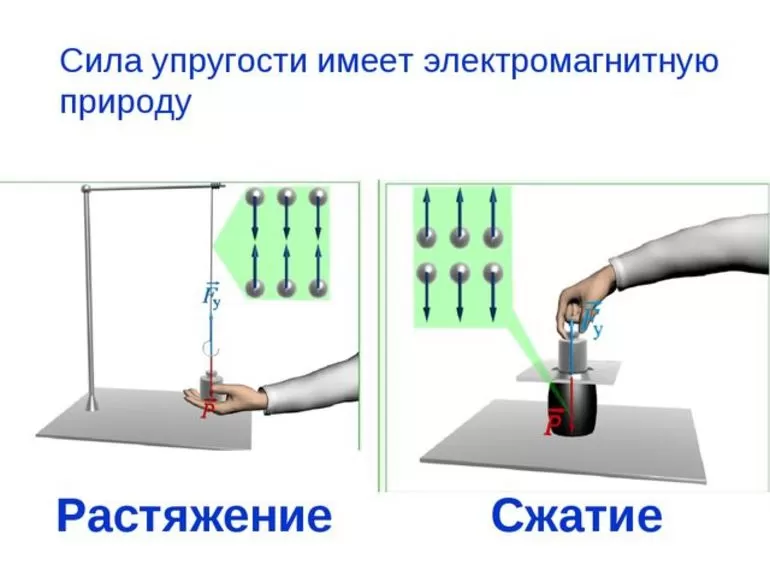
Всегда важно убедиться, что направление восстанавливающей силы задаётся последовательно при приближении к механическим задачам, связанным с упругостью. Для простых задач часто можно интерпретировать расширение X как одномерный вектор, в этом случае результирующая сила также будет одномерным вектором, а отрицательный знак в законе Гука даст правильное направление силы.
Однако успешность применения принципа зависит от того, при каких условиях он выполняется. Закон Гука является лишь линейным приближением первого порядка к реальному отклику пружин (и других упругих тел) на приложенные силы и имеет границы применимости, работая только в ограниченной системе координат.
Поскольку ни один материал не может быть сжат сильнее определённого минимального размера (или растянут за пределы максимального размера) без некоторой постоянной деформации или изменения состояния, он применяется только до тех пор, пока задействовано ограниченное количество силы или деформации. Фактически многие материалы заметно отклонятся от закона Гука задолго до того, как будут достигнуты эти пределы упругости.
С другой стороны, этот закон является точным приближением для большинства твёрдых тел, пока силы деформации достаточно слабы.
По этой причине он широко используется во всех областях науки (например, в сопромате) и техники, а ещё является основой многих дисциплин, таких как сейсмология, молекулярная механика и акустика.
Это также принцип, стоящий за пружинной шкалой, манометром и колесом баланса механических часов.
Поскольку общие напряжения и деформации могут иметь несколько независимых компонентов, «коэффициент пропорциональности» может больше не быть просто одним действительным числом, а скорее линейной картой (тензором), которая может быть представлена матрицей действительных чисел.
В этом обобщённом виде закон позволяет вывести связь между деформацией и напряжением для сложных объектов, с точки зрения внутренних свойств материалов, из которых они изготовлены. Например, можно сделать вывод, что однородный стержень с равномерным поперечным сечением будет вести себя как простая пружина при растяжении, с жёсткостью K, прямо пропорциональной его площади поперечного сечения и обратно пропорциональной его длине.
Модуль Юнга
Модуль Юнга (также известный как модуль упругости) — это число, которое измеряет сопротивление материала упругой деформации. Оно названо в честь физика XVII века Томаса Юнга. Чем жёстче материал, тем выше его модуль Юнга.
Это значение обычно обозначается символом E и записывается как E = σ/ε, где:
- σ (сигма) представляет собой одноосное напряжение, или одноосное усилие на единицу поверхности в паскалях.
- ε (эпсилон) является деформацией или пропорциональной деформацией (изменение длины, делённое на исходную длину).
Модуль Юнга можно определить при любом напряжении, но там, где он подчиняется закону Гука, это постоянная величина. Можно непосредственно получить постоянную пружины k из модуля материала, области A, к которой приложена сила (поскольку напряжение зависит от площади), и номинальной длины материала L.
Практическое использование
Модуль Юнга позволяет рассчитать изменение размера стержня из изотропного упругого материала при растягивающих или сжимающих нагрузках. Например, он предсказывает, насколько образец материала растягивается при растяжении или укорачивается при сжатии.
Модуль непосредственно относится к случаям одноосного напряжения, то есть растягивающего или сжимающего напряжения в одном направлении и отсутствия напряжения в других направлениях.
Он также используется, чтобы найти отклонение, которое будет появляться в статически определённом луче, когда нагрузка приложена в точке между опорами луча. Другие вычисления обычно требуют использования одного дополнительного упругого свойства, такого как модуль сдвига, модуль объёма или коэффициент Пуассона. Любые два из этих параметров достаточны для полного описания упругости в изотропном материале.
Виды материалов
Сталь, углеродное волокно и стекло среди прочих обычно считаются линейными материалами, в то время как другие материалы, такие как резина и грунты, являются нелинейными. Однако это не абсолютная классификация: если к нелинейному материалу применяется небольшое напряжение, отклик будет линейным. Например, поскольку линейная теория предполагает обратимость, было бы абсурдно использовать её для описания разрушения стального моста под большой нагрузкой.
Модуль не всегда одинаков во всех ориентациях материала. Большинство металлов и керамики, наряду со многими другими материалами, являются изотропными, и их механические свойства одинаковы во всех ориентациях. Тем не менее металлы и керамика могут быть обработаны определёнными примесями, чтобы сделать их структуры зерна направленными.
Эти материалы затем становятся анизотропными, и модуль Юнга будет меняться в зависимости от направления вектора силы. Анизотропия также наблюдается во многих композитах. Например, углеродное волокно имеет гораздо более высокий модуль Юнга, когда сила нагружена параллельно волокнам (вдоль зерна). Другие такие материалы включают дерево и железобетон. Инженеры могут использовать это явление при создании конструкций.
Поскольку производители пружинных весов ожидают, что их продукт будет использоваться вертикально (например, рыбаком, измеряющим массу своей добычи), шкала откалибрована для учёта массы пружины и крючка. Это даст неверный абсолютный результат, если использовать его для измерения горизонтальной силы.
Тем не менее закон Гука говорит, что существует линейная зависимость между силой и растяжением. Из-за этого всё ещё можно рассчитывать на шкалу относительных измерений при горизонтальном использовании. Некоторые пружинные весы имеют регулировочный винт, который позволяет калибровать нулевую точку, устраняя эту проблему.
Источник
