Формула расчета прочности на растяжение при изгибе

2.4. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ Основной задачей расчета конструкции на растяжение является обеспечение ее прочности в условиях эксплуатации. Условие прочности – оценка прочности элемента конструкции, сводящаяся к сравнению расчетных напряжений с допускаемыми: σ≤рσ[р ]; σ с ≤[ с],σ (2.9) где σр и σс – наибольшие расчетные растягивающие и сжимающие напряжения; [σр] и [σс] – допускаемые напряжения при растяжении и сжатии. Допускаемое напряжение – наибольшее напряжение, которое можно допустить в элементе конструкции при условии его безопасной, долговечной и надежной работы: Здесь σпред – предельное напряжение (состояние), при котором конструкция перестает удовлетворять эксплуатационным требованиям; им мо- гут быть предел текучести, предел прочности, предел выносливости, пре- дел ползучести и др. Для конструкций из пластичных материалов при определении допускаемых напряжений используют предел текучести σт (рис. 2.4, а). Это связано с тем, что в случае его превышения деформации резко возрастают при незначительном увеличении нагрузки и конструкция перестает удовлетворять условиям эксплуатации. Допускаемое напряжение в этом случае определяют как Для хрупких материалов (чугун, бетон, керамика) где σвр и σвс – пределы прочности при растяжении и сжатии (рис. 2.4, б). Здесь [n] – нормативный коэффициент запаса прочности. В зависимости от той предельной характеристики, с которой сравнивают расчетное напряжение σ, различают [nт] – нормативный коэффициент запаса прочности по отношению к пределу текучести σт и [nв] – нормативный коэффициент запаса прочности по отношению к пределу прочности σв. Запас прочности – отношение предельно допустимой теоретической нагрузки к той нагрузке, при которой возможна безопасная работа конструкции с учетом случайных перегрузок, непредвиденных дефектов и недостоверности исходных данных для теоретических расчетов. Нормативные коэффициенты запаса прочности зависят: − от класса конструкции (капитальная, временная), − намечаемого срока эксплуатации, − условий эксплуатации (радиация, коррозия, загнивание), − вида нагружения (статическое, циклическое, ударные нагрузки) − неточности задания величины внешних нагрузок, − неточности расчетных схем и приближенности методов расчета − и других факторов. Нормативный коэффициент запаса прочности не может быть единым на все случаи жизни. В каждой отрасли машиностроения сложились свои подходы, методы проектирования и приемы технологии. В изделиях общего машиностроения принимают [nт] = 1,3 – 2,2; [nв] = 3 – 5. Вероятность выхода из строя приближенно можно оценить с помощью коэффициента запаса в условии прочности: n = 1 соответствует вероятности невыхода из строя 50 %; n = 1,2 соответствует вероятности невыхода из строя 90 %; n = 1,5 соответствует вероятности невыхода из строя 99 %; n = 2 соответствует вероятности невыхода из строя 99,9 %. Для неответственных деталей n = 2 много. Для ответственных – мало. Так для каната подъемного лифта это означает на 1000 подъемов одно падение. При расчете конструкций на прочность встречаются три вида задач, которые вытекают из условия прочности а) поверочный расчет (проверка прочности). Известны усилие N и площадь A. Вычисляют σ = N/A и, сравнивая его с предельным σт или σв (для пластичного и хрупкого материалов соответственно), находят фактический коэффициент запаса прочности который затем сопоставляют с нормативным [n]; б) проектный расчет (подбор сечения). Известны внутреннее усилие N и допускаемое напряжение [σ]. Определяют требуемую площадь поперечного сечения стержня в) определение грузоподъемности (несущей способности). Известны площадь А и допускаемое напряжение [σ]. Вычисляют внутреннее усилие N≤N[ ] = ⋅[σ]A, (2.15) а затем в соответствие со схемой нагружения – величину внешней нагрузки F ≤ [F].

Условие прочности балки при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое. Полагая, что гипотеза о ненадавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения в поперечном сечении вычислять при поперечном изгибе по той же формуле, что и при чистом изгибе. Вопрос о проверке прочности балки на касательные напряжения, а также о расчете балок на жесткость будет изложен в последующих параграфах.

Расчетная формула на прочность при изгибе имеет вид

и читается так: нормальное напряжение в опасном сечении, вычисленное по формуле а = Mnm&x)W , не должно превышать допускаемое. Допускаемое нормальное напряжение при изгибе выбирают таким же, как и при растяжении и сжатии. Максимальный изгибающий момент определяют из эпюр изгибающих моментов или расчетом. Так как момент сопротивления изгибу Wв расчетной формуле стоит в знаменателе, то чем больше W, тем меньше будут расчетные напряжения.

Определим моменты сопротивления изгибу наиболее распространенных сечений.

1. Прямоугольник bxh (рис. 6.15):

Рис. 6.15

Если балку прямоугольного сечения положить плашмя, то КР =hb2 /б , тогда

следовательно, при прочих равных условиях максимальные нормальные напряжения а’ у прямоугольной балки, положенной плашмя, будут больше, чем у той же балки, когда ее наибольший габаритный размер h вертикален (имеется в виду, что изгиб происходит в вертикальной плоскости).

Из сказанного следует правило: для обеспечения максимальной прочности ось, относительно которой момент инерции максимален, должна быть нейтральной.

2. Круг диаметром d:

3. Кольцо с размерами Dxd:

Момент сопротивления кольцевого сечения нельзя вычислять как разность моментов сопротивлений большого и малого кругов. Нетрудно подсчитать, что при одинаковой площади поперечного сечения, то есть при одинаковом расходе материала момент сопротивления кольцевого сечения больше момента сопротивления сплошного круглого сечения.

Так как вблизи нейтральной оси материал мало напряжен, то выгодно больше материала располагать дальше от нейтральной оси. Поэтому в машиностроении редко применяют металлические балки прямоугольного сечения, но весьма широко распространены прокатные профильные балки таврового, двутаврового, углового, швеллерного и других сечений. Моменты инерции, моменты сопротивления и другие характеристики прокатных фасонных профилей стандартных размеров даются в таблицах ГОСТа.

Для балок, материал которых неодинаково работает на растяжение и сжатие (например, чугун), целесообразно применять профили, не симметричные относительно нейтральной оси, например тавровый или П-образный. Так как у несимметричного профиля при изгибе возникают неодинаковые напряжения растяжения и сжатия, то сечение, например, чугунной балки выгодно располагать так, чтобы меньшие напряжения были в зоне растянутых, а большие — в зоне сжатых волокон (рис. 6.16).

Рис. 6.16

Проведем сравнение экономичности по массе балок двутаврового, прямоугольного и квадратного сечений. Предположим, что из расчетного уравнения мы определили момент сопротивления изгибу балки: W = Л/итахДа] = 1,2-10_3 м3 =1200 см3. По таблицам ГОСТа выбираем двутавровый профиль № 45 с площадью поперечного сечения Л№ = — 83 см2.

Определим размеры прямоугольного сечения, полагая И = 2b:

Отсюда b = lj1200-3/2 = 12,2 см; И = 2Ь = 24,4 см; Апр=ЬИ = 12,2 * • 24,4 = 297 см2.

При прочих равных условиях массы балок пропорциональны площадям поперечных сечений и, следовательно, отношение их масс равно Апр/Аав = 297/83 » 3,5 . Таким образом, балка прямоугольного сечения в три с половиной раза тяжелее балки двутаврового профиля при одинаковой прочности и прочих равных условиях.

Определим размеры квадратного сечения со стороной а: поскольку W = a3/6 = 1200 см2, то
см; АЮ}=а1 = 375 см2;

Лсв/Аш = 375/83 « 4,5. Таким образом, балка квадратного сечения в четыре с половиной раза тяжелее балки двутаврового профиля при одинаковой прочности и прочих равных условиях.

Для балок из хрупкого материала (например, чугуна) составляют два условия прочности — на сжатие и на растяжение, так как хрупкий материал неодинаково сопротивляется сжатию и растяжению.

Пример 6.5

Определить номер профиля консольной балки двутаврового сечения, если допускаемое напряжение при изгибе [а] = 120 МПа, F= 2000 Н, q = 4000 Н/м, /= 2 м (рис. 6.17).

Рис. 6.17

Решение. Очевидно, что у данной балки, работающей на изгиб, максимальный изгибающий момент будет в заделке и определится по формуле Мнтах = -Fl-ql2/8 . Подставив данные, получим абсолютное значение момента

Расчетное уравнение на прочность при изгибе имеет вид атах = = MKmax/Wx [а], откуда

Найдя по таблицам сортамента ближайшее большее значение для Wx, выбираем двутавровое сечение № 12, для которого Wx = 58,4 см2. Если сечение балки повернуть на 90°, то есть расположить полки вертикально, а стенку — горизонтально (рис. 6.17), то потребуется профиль № 30 (при таком расположении сечения двутавр подбирается по 1VX). В этом случае балка окажется в три раза тяжелее.

Пример 6.6

Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 6.18, если F= 20 кН, q = 20 кН/м, т = 8 кН м, а = 0,8 м. Проверить балку на прочность, если ее профиль — двутавр № 20, а допускаемое напряжение [а] = 150 МПа.

Решение. Определим опорные реакции RBw RD, составив уравнение моментов относительно точек BwD.

Подставив данные и произведя вычисления, получим RD = 22 кН.

Подставив данные и произведя вычисления, получим RB = 14 кН.

Рис. 6.18

Построение эпюры Q. На первом участке Qx = 0, так как алгебраическая сумма сил пары всегда равна нулю. На втором участке Q2 = Rg= 14 кН. На третьем участке 03 = RB — F= 14 — 20 = —6 кН. На этих участках эпюра Q изображается прямыми линиями, параллельными оси.

Четвертый участок рассмотрим, взяв начало координат на правом конце балки: 04 = qz, где z изменяется от 0 до а. Тогда при z = 0 04 = 0, при z = aQ4 = = qa = 20 • 0,8 = 16 кН. На этом участке эпюра изображается прямой наклонной линией. В точке D эпюра Q имеет «скачок», равный опорной реакции RD.

Построение эпюры Мн. На первом участке М1и = —т = —8 кН. На втором и третьем участках строим эпюру по значениям изгибающего момента на границах участков: в сечении В имеем М2н = —т = —8 кН; в сечении С имеем М2к = —т + RB ? а = — 8 + 14 • 0,8 = 3,2 кН м; в сечении D имеем М3и = —т + + RB ? За -F- 2а = — 8 + 14 • 3 • 0,8 — 20 • 2 • 0,8 = —6 кН м. На первых трех участках эпюра Мц изображается прямыми линиями.

Четвертый участок рассмотрим, взяв начало координат на правом конце балки: М4и = -qz212 , где z изменяется от 0 до а. Тогда при z = 0 М4и = 0, при Z = а М4и = —qa2/2 = —20 • 0,82/2= —6,4 кН м. На этом участке эпюра Ми — дуга параболы.

Проверка балки на прочность. Наибольший изгибающий момент будет на первом участке: | Митах = 8 кН м. Расчетная формула на прочность при изгибе: а = MKmax/Wx [а]. По таблицам сортамента находим значение момента сопротивления для двутавра № 20: Wx = 184 см3 = 184-10 6 м3. Подставляя значения и учитывая размерности, получим

Условие прочности а

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент Mx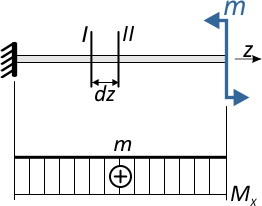

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.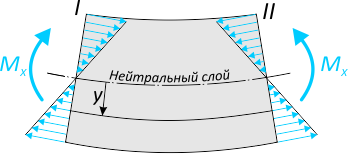

Закон распределения нормальных напряжений по высоте сечения выражается формулой: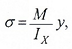

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
Ix — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y1=y2=h/2: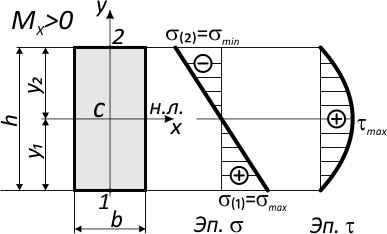

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.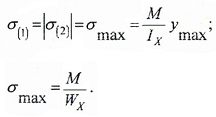

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2: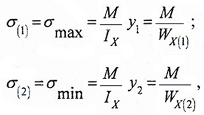

где: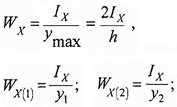

WX — осевой момент сопротивления симметричного сечения;
WX(1) и WX(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.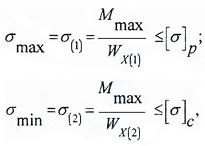

Здесь:
Mmax — максимальное значение изгибающего момента, определяемого по эпюре Mx;
[σ], [σ]р, [σ]с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]с>[σ]р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
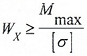
3. Определение максимально допустимой нагрузки
   

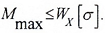
Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского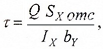

где
Sx отс — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
by — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Qmax: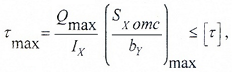

где [τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

1. По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
2. По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
3. По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда Mmax и Qmax действуют в одном и том же сечении балки).

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид: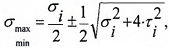

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений: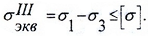

Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >