Формула для расчета удлинения при растяжении

Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ
ИНСТИТУТ
СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
им. В.А. КУЧЕРЕНКО ГОССТРОЯ СССР
РЕКОМЕНДАЦИИ
ПО МЕТОДИКЕ ОПРЕДЕЛЕНИЯ
ОТНОСИТЕЛЬНОГО РАВНОМЕРНОГО
УДЛИНЕНИЯ СТРОИТЕЛЬНЫХ
СТАЛЕЙ ПРИ ИСПЫТАНИИ
НА РАСТЯЖЕНИЕ
Утверждены директором ЦНИИСК
им. В.А.
Кучеренко
27 апреля 1979 г.
МОСКВА — 1980
Рекомендации распространяются
на стальной
прокат для строительных металлических
конструкций и устанавливают методы определения относительного равномерного
удлинения как характеристики, нормируемой
техническими условиями, так и необходимой при
проведении научно-исследовательских работ.
Рекомендации предназначены
для инженерно-технических работников заводских
лабораторий (заводов строительных металлоконструкций)
и научно-исследовательских организаций.
Рис. 2.
СОДЕРЖАНИЕ
При работе стали в
конструкциях характеристика относительного равномерного удлинения играет важную роль для
оценки способности металла пластически деформироваться. Эта характеристика
имеет большее значение, чем нормируемое в настоящее время полное относительное
удлинение согласно ГОСТ 1497-73. До настоящего времени для определения равномерного
относительного удлинения в основном использовалась методика, описанная в
стандарте на арматурные стали, где не предусмотрены плоские образцы.
Настоящее руководство
распространяется на стальной толстолистовой, широкополосный универсальный и
фасонный (уголок, швеллер, балка) прокат толщиной от 4 до 40 мм, независимо от
его прочностных свойств, предназначенный для изготовления
строительных металлических конструкций, и
устанавливает методы определения относительного равномерного удлинения при
статических испытаниях
на растяжение при нормальных температурах ![]() .
.
Применение методов
определения относительного равномерного удлинения предусматривается в
стандартах и технических условиях на соответствующие виды проката,
предназначенного для строительных металлических конструкций.
Термины и определения,
принятые в настоящих рекомендациях, согласованы с ГОСТ 1497-73 «Металлы. Методы испытания на растяжение».
Относительное равномерное
удлинение определяется одновременно с относительным удлинением после разрыва.
Настоящие рекомендации
разработаны Отделением прочности и новых форм металлических конструкций и
Отделением испытаний конструкций ЦНИИСК им. Кучеренко Госстроя СССР (составили кандидаты
технических наук Потапов В.Н. и Жулев Ю.К.) на
основании материалов исследований, выполненных
в период 1976-78 гг.
Дирекция ЦНИИСК
им. Кучеренко
1.1. При испытании на
растяжение по определению относительного равномерного удлинения принимаются
следующие обозначения и определения:
l — рабочая длина в мм — часть образца с постоянной площадью поперечного сечения между его
головкой или участком для захвата;
l0 — начальная расчетная длина образца в мм, на которой
определяется удлинение после разрыва;
lпр — начальная расчетная длина участка образца в мм, на которой
определяется равномерное удлинение;
lкр — конечная расчетная длина участка образца в мм, не
включающая место разрыва;
lт — установочная база измерителя деформаций в мм;
d0 — начальный диаметр рабочей части цилиндрического образца до
разрыва в мм;
F0 — начальная площадь поперечного сечения рабочей части образца в мм2;
Fкр — конечная площадь поперечного сечения рабочей части образца после
разрыва, определяемая в расчетной части равномерного
относительного удлинения в мм2.
1.2. Характеристики
механических свойств, получаемых при испытании на растяжение, имеют следующие
обозначения и определения:
δр — относительное равномерное удлинение после разрыва в % — отношение приращения расчетной длины образца (lкр — lнр) на участке, не
включающем место разрыва, к соответствующей первоначальной длине lнр;
ψp — относительное равномерное сужение в % — отношение изменения
площади поперечного сечения образца (F0 — Fкр) после разрыва на участке, не включающем место разрыва, к начальной площади поперечного сечения;
Pвр — максимальная осевая растягивающая нагрузка в кГс, действующая
на образец до образования шейки.
2.1. Для определения
относительного равномерного удлинения при испытании на растяжение применяют
пропорциональные плоские образцы типов I и II с начальной расчетной длиной ![]() а также пропорциональные цилиндрические образцы типов I — VII
а также пропорциональные цилиндрические образцы типов I — VII
с l0 = 10d0 по ГОСТ 1497-73.
2.2. Рабочая длина плоского
образца должна составлять
![]()
2.3. При испытании
толстолистового широкополосного и уголкового проката применяют, как правило, плоские образцы. При
испытании швеллерного и двутаврового проката применяют, в основном,
цилиндрические образцы; допускается применение плоских образцов с одной прокатной и другой
обработанной поверхностями.
Плоские образцы должны сохранять
поверхностные слои проката. При толщине проката свыше 25 мм:
— испытания проводят на
плоских образцах толщиной 25 мм с одной прокатной поверхностью;
— допускается применять
плоские образцы
с обеими прокатными поверхностями, принимая при этом ширину образца не менее 50
мм и расчетную длину ![]() .
.
2.4. Измерение начальной и
конечной расчетных длин, размеров поперечного
сечения образца производят с точностью до 0,1 мм.
2.5. На рабочей части образца
рекомендуется наносить разметку — неглубокие керны, риски или иные метки через каждые 5 или
10 мм.
3.1. Для испытаний применяют
разрывные и универсальные машины всех систем, если они соответствуют
требованиям ГОСТ 1497-73, ГОСТ 7855-74
и требованиям
стандартов на стали для строительных металлических конструкций.
3.2. При проведении испытаний
должны соблюдаться следующие основные условия:
а) надежное центрирование
образца в захватах испытательной машины;
б) плавность нагружения;
в) скорость перемещения активного захвата при
испытании до предела текучести долина быть не
более 0,01, за пределом текучести не более 0,2 длины расчетной части образца,
выраженной в мм/мин.
4.1. При текущих испытаниях
определение относительного равномерного
удлинения может производиться по одному из
следующих методов:
Первый метод
Относительное равномерное
удлинение δр определяют вне участка разрыва (предпочтительней на
большей части разрушенного образца) на начальной расчетной длине, равной 50 мм.
При этом расстояние от места разрыва до
ближайшей точки (риски) начальной расчетной
длины lпр должно быть не менее 3b0*) (с округлением до ближайшей удаленной
разметочной риски от места разрыва образца где
b0 — начальная ширина образца (рис. 1).
______________
*)
В случае цилиндрических образцов вместо b0 следует d0.
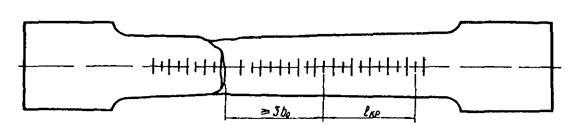
Рис. 1
Относительное равномерное
удлинение δр в процентах вычисляют по формуле
![]()
Второй метод
Относительное равномерное
удлинение δр в % вычисляют по следующей формуле
![]()
где ψр — относительное равномерное сужение в %, вычисленное по формуле
![]()
Измерение площади Fкр производится на расстоянии от места
разрыва не менее 4b0.
Третий метод*)
______________
*) Этот метод
допускает использование образцов с пятикратной расчетной длиной.
Относительное равномерное
удлинение δр определяют графически по диаграмме растяжения (рис. 2), записываемой соответствующим измерителем деформаций, установленным непосредственно на
образце.
Масштаб по оси деформаций
должен быть не менее 50:1.
Примечание. Определение δр производится на
участке диаграммы растяжения, заканчивающемся точкой В, которая соответствует
началу достижения максимальной нагрузки Рвр.
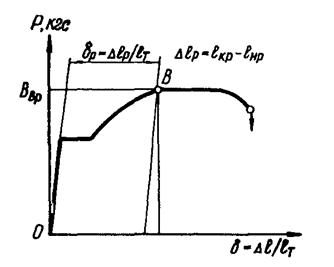
Рис. 2
4.2. Относительное
равномерное удлинение вычисляют с округлением до 0,5 %. При этом доли до 0,25 %
отбрасывают, а доли в 0,25 % и более принимают за 0,5 % (см. приложение).
4.3. Испытание считается
недействительным:
— при разрыве
образца по кернам (рискам), если при этом какая-либо
характеристика механических свойств по своей величине не отвечает установленным требованиям;
— при разрыве
образца в захватах испытательной машины или за пределами расчетной длины;
— при обнаружении ошибок в
проведении испытаний или записи результатов
испытаний.
В указанных случаях испытание
на растяжение должно быть повторено на отобранных от той же партии или плавки
новых образцах.
По первому методу (рис. 1)
Начальная расчетная длина lнр = 50
мм;
Конечная расчетная длина lкр = 58,4 мм,
![]()
По второму методу
Начальная площадь поперечного сечения
(10×30 мм) образца F0 = 300 мм2.
Конечная площадь поперечного
сечения образца (замеренная на расстоянии 4b0 от места разрыва) Fкр = 258 мм2
|
|
Источник
Растяжение (сжатие) – это такой вид нагружения стержня, при котором в его поперечном сечении возникает внутренняя продольная сила Ν, действующая вдоль центральной оси z.
Продольная сила Ν – это равнодействующая всех внутренних нормальных сил в сечении. Для вычисления продольной силы применяется метод сечений.

Продольная сила Ν численно равна алгебраической сумме проекций всех сил, действующих по одну сторону от рассматриваемого сечения, на продольную ось бруса.
Правило знаков для продольной силы Ν: при растяжении продольная сила положительна, при сжатии – отрицательна.

График изменения продольных сил по длине стержня называется эпюрой. Эпюра N строится методом сечений на характерных участках бруса. Строится эпюра для использования ее при расчете бруса на прочность. Она дает возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.
При растяжении (сжатии) возникают только нормальные напряжения. Согласно гипотезе Я. Бернулли (или гипотеза плоских сечений) в поперечных сечениях, удаленных от места приложения нагрузок, нормальные напряжения распределяются по сечению практически равномерно, а сами сечения, перпендикулярные к оси стержня z, остаются плоскими в процессе нагружения.
Нормальные напряжения в сечении при растяжении (сжатии) вычисляются по формуле

где А – площадь поперечного сечения.
Правило знаков для σ совпадает с правилом знаков для N.
В наклонном сечении, нормаль к которому составляет угол α с осью стержня z,

При растяжении в продольном направлении стержень удлиняется, а его поперечные размеры уменьшаются, при сжатии, напротив, в продольном направлении стержень укорачивается, а его поперечные размеры увеличиваются; Δℓ — абсолютное удлинение или укорочение участка стержня длиной ℓ, Δb – абсолютная поперечная деформация.
Относительное удлинение или укорочение участка стержня длиной ℓ, называемое линейной деформацией, определяется следующим образом
ε=Δℓ/ℓ.
Экспериментально установлено, что в определенной области нагрузок при упругом поведении материала между нормальными напряжениями и линейными деформациями существует линейная зависимость (закон Гука для напряжений)
σ=εЕ,
где Е – модуль продольной упругости или модуль Юнга, это физическая const. Для каждого из материалов величина модуля упругости имеет свое значение:
сталь, Е = 2.105 МПа,
медь, Е = 1.105 МПа,
алюминий, Е = 0,7.105 МПа.
Значение модуля упругости устанавливается экспериментально.
Согласно закону Гука (данную запись называют законом Гука для деформаций)
Δℓ=Νℓ/ЕА
Произведение ЕА – называется жесткостью стержня при растяжении – сжатии.
Перемещение произвольного сечения ступенчатого стержня
w=∑Δℓi
Относительная поперечная деформация:
ε′=Δb/b
где b – поперечный размер стержня.
Эксперименты также показывают, что в упругой стадии деформирования между продольной и поперечной деформациями существует взаимосвязь
μ =│ε′⁄ε│ — const,
где μ — коэффициент Пуассона, берется по модулю ,поскольку у продольной и поперечной деформации разные знаки (при растяжении продольные волокна увеличиваются, а поперечные уменьшаются в размере).
Для твердых материалов имеет значения коэффициент Пуассона
0≤μ ≤0,5
Изменение температуры стержня вызывает его удлинение (при нагревании) или укорочение (при охлаждении)

где — a- коэффициент линейного температурного расширения; Δtº=(tºк-tºн) — изменение температуры между значениями начальным (tºн) и конечным (tºк).
Статически неопределимыми называют системы, имеющие лишние связи – внешние или внутренние.
Для определения внутренних усилий в таких системах недостаточно рассматривать только уравнения равновесия.
В этом случае требуются дополнительные уравнения, число которых равно количеству лишних связей. Дополнительные уравнения составляются на основе анализа картины деформирования системы и использования законов деформирования ее элементов.
Алгоритм решения подобных задач включает следующее:
1) Статическая часть. Составляются уравнения равновесия с включением неизвестных усилий, действующих по направлению лишних связей.
2) Геометрическая часть. Составляются уравнения, описывающие взаимосвязь перемещений характерных точек, удлинений и укорочений отдельных стержней между собой.
3) Физическая связь. Записываются законы деформирования отдельных стержней системы.
Порядок расчета статически неопределимых брусьев
- Задаться направлениями возможных опорных реакций и составить уравнение статики для всей системы в целом.
- Определить степень статической неопределимости и использовать метод сечений с целью выразить неизвестные усилия через неизвестные опорные реакции. При этом неизвестные продольные силы (N) следует предполагать положительными и поэтому направлять «от сечения».
- Сформулировать условие совместности деформаций участков бруса.
- В процессе превращения условия совместности в уравнение совместности деформаций различий в характере деформаций участков не учитывать.
Порядок расчета статически неопределимых шарнирно-стержневых систем
- Задаться направлениями опорных реакций, но уравнений равновесия для всей системы не составлять, а сразу использовать метод сечений и составить уравнения статики для выделенной части системы.
- Определить степень статической неопределимости как разницу между количеством всех неизвестных, оказавшихся в уравнениях статики, и числом самих этих уравнений.
- Рассмотреть (изобразить) любую возможную картину деформаций системы и из ее анализа сформулировать условия совместности деформаций стержней системы (столько, какова степень статической неопределимости).
- В процессе преобразования условий совместности в уравнения совместности деформаций обязательно учитывать различие в характере деформаций стержней (т.е. вводить удлинение со знаком «плюс», а укорочение со знаком «минус») в соответствии с той картиной деформации, которую мы рассматриваем.
Источник
