Единицу измерения разрушающего напряжения на растяжение
14Ноя
By: Семантика
Без рубрики
Comment: 0
Содержание статьи
- Предел прочности
- Как производится испытание на прочность
- Виды ПП
- Предел прочности на растяжение стали
- Предел текучести и временное сопротивление
- Усталость стали
- Предел пропорциональности
- Как определяют свойства металлов
- Механические свойства
- Классы прочности и их обозначения
- Формула удельной прочности
- Использование свойств металлов
- Пути увеличения прочностных характеристик
При строительстве объектов обязательно необходимо использовать расчеты, включающие подробные характеристики стройматериалов. В обратном случае на опору может быть возложена слишком большая, непосильная нагрузка, из-за чего произойдет разрушения. Сегодня поговорим о пределе прочности материала при разрыве и натяжении, расскажем, что это такое и как работать с этим показанием.
Предел прочности
ПП – будем использовать это сокращение, а также можно говорить об официальном сочетании «временное сопротивление» – это максимальная механическая сила, которая может быть применена к объекту до начала его разрушения. В данном случае мы не говорим о химическом воздействии, но подразумеваем, что нагревание, неблагоприятные климатические условия, определенная среда могут либо улучшать свойства металла (а также дерева, пластмассы), либо ухудшать.
Ни один инженер не использует при проектировании крайние значения, потому что необходимо оставить допустимую погрешность – на окружающие факторы, на длительность эксплуатации. Рассказали, что называется пределом прочности, теперь перейдем к особенностям определения.
Как производится испытание на прочность
Изначально особенных мероприятий не было. Люди брали предмет, использовали его, а как только он ломался, анализировали поломку и снижали нагрузку на аналогичное изделие. Теперь процедура гораздо сложнее, однако, до настоящего времени самый объективный способ узнать ПП – эмпирический путь, то есть опыты и эксперименты.
Все испытания проходят в специальных условиях с большим количеством точной техники, которая фиксирует состояние, характеристики подопытного материала. Обычно он закреплен и испытывает различные воздействия – растяжение, сжатие. Их оказывают инструменты с высокой точностью – отмечается каждая тысячная ньютона из прикладываемой силы. Одновременно с этим фиксируется каждая деформация, когда она происходит. Еще один метод не лабораторный, а вычислительный. Но обычно математический анализ используется вместе с испытаниями.
Определение термина
Образец растягивается на испытательной машине. При этом сначала он удлиняется в размере, а поперечное сечение становится уже, а затем образуется шейка – место, где самый тонкий диаметр, именно здесь заготовка разорвется. Это актуально для вязких сплавов, в то время как хрупкие, к ним относится чугун и твердая сталь, растягиваются совсем незначительно без образования шейки. Подробнее посмотрим на видео:
Виды ПП
Временное сопротивление разрыву определяют по различным воздействиям, согласно этому его классифицируют по:
- сжатию – на образец действуют механические силы давления;
- изгибу – деталь сгибают в различные стороны;
- кручению – проверяется пригодность для использования в качестве крутящегося вала;
- растяжению – подробный пример проверки мы привели выше.
Предел прочности на растяжение стали
Стальные конструкции давно заменили прочие материалы, так как они обладают отличными эксплуатационными характеристиками – долговечностью, надежностью и безопасностью. В зависимости от применяемой технологии, он подразделяется на марки. От самой обычной с ПП в 300 Мпа, до наиболее твердой с высоким содержанием углерода – 900 Мпа. Это зависит от двух показателей:
- Какие способы термообработки применялись – отжиг, закалка, криообработка.
- Какие примеси содержатся в составе. Одни считаются вредными, от них избавляются для чистоты сплава, а вторые добавляют для укрепления.
Предел текучести и временное сопротивление
Новый термин обозначается в технической литературе буквой Т. Показатель актуален исключительно для пластичных материалов и обозначает, как долго может деформироваться образец без увеличения на него внешней нагрузки.
Обычно после преодоления этого порога кристаллическая решетка сильно меняется, перестраивается. Результатом выступают пластические деформации. Они не являются нежелательными, напротив, происходит самоупрочнение металла.
Усталость стали
Второе название – предел выносливости. Его обозначают буквой R. Это аналогичный показатель, то есть он определяет, какая сила может воздействовать на элемент, но не в единичном случае, а в цикле. То есть на подопытный эталон циклично, раз за разом действуют определенные давления. Среднее количество повторений – 10 в седьмой степени. Именно столько раз металл должен без деформаций и потери своих характеристик выдержать воздействие.
Если проводить эмпирические испытания, то потребуется множество времени – нужно проверить все значения силы, прикладывая ее по множеству циклов. Поэтому обычно коэффициент рассчитывается математически.
Предел пропорциональности
Это показатель, определяющий длительность оказываемых нагрузок к деформации тела. При этом оба значения должны изменяться в разный степени по закону Гука. Простыми словами: чем больше оказывается сжатие (растяжение), тем сильнее деформируется образец.
Значение каждого материала находится между абсолютной и классической упругостью. То есть если изменения обратимы, после того как сила перестала действовать (форма стала прежняя – пример, сжатие пружины), то такие параметры нельзя называть пропорциональными.
Как определяют свойства металлов
Проверяют не только то, что называют пределом прочности, но и остальные характеристики стали, например, твердость. Испытания проводят следующим образом: в образец вдавливают шарик или конус из алмаза – наиболее прочной породы. Чем крепче материал, тем меньше след остается. Более глубокие, с широким диаметром отпечатки остаются на мягких сплавах. Еще один опыт – на удар. Воздействие оказывается только после заранее сделанного надреза на заготовке. То есть разрушение проверяется для наиболее уязвимого участка.
Механические свойства
Различают 5 характеристик:
- Предел прочности стали при растяжении и на разрыв это – временное сопротивление внешним силам, напряжение, возникающее внутри.
- Пластичность – это возможность деформироваться, менять форму, но сохранять внутреннюю структуру.
- Твердость – готовность встретиться с более твердым материалом и не получить значительных ущербов.
- Ударная вязкость – способность сопротивляться ударам.
- Усталость – длительность сохранения качеств под воздействием цикличных нагрузок.
Классы прочности и их обозначения
Все категории записаны в нормативных документах – ГОСТах, по ним все российские предприниматели изготавливают любой металлопрокат и прочие металлические изделия. Вот соответствие обозначения и параметра в таблице:
| Класс | Временное сопротивление, Н/мм2 |
| 265 | 430 |
| 295 | 430 |
| 315 | 450 |
| 325 | 450 |
| 345 | 490 |
| 355 | 490 |
| 375 | 510 |
| 390 | 510 |
| 440 | 590 |
Видим, что для некоторых классов остается одинаковыми показатели ПП, это объясняется тем, что при равных значениях у них может различаться текучесть или относительное удлинение. В зависимости от этого возможна различная максимальная толщина металлопроката.
Формула удельной прочности
R с индексом «у» – обозначение данного параметра в физике. Рассчитывается как ПП (в записи – R) поделенное на плотность – d. То есть этот расчет имеет практическую ценность и учитывает теоретические знания о свойствах стали для применения в жизни. Инженеры могут сказать, как меняется временное сопротивление в зависимости от массы, объема изделия. Логично, что чем тоньше лист, тем легче его деформировать.
Формула выглядит так:
Ry = R/d
Здесь будет логичным объяснить, в чем измеряется удельный предел прочности. В Н/мм2 – это вытекает из предложенного алгоритма вычисления.
Использование свойств металлов
Два важных показателя – пластичность и ПП – взаимосвязаны. Материалы с большим первым параметром намного медленнее разрушаются. Они хорошо меняют свою форму, подвергаются различным видам металлообработке, в том числе объемной штамповке – поэтому из листов делают элементы кузова автомобиля. При малой пластичности сплавы называют хрупкими. Они могут быть очень твердыми, но при этом плохо тянуться, изгибаться и деформироваться, например, титан.
Сопротивление
Есть два типа:
- Нормативное – прописано для каждого типа стали в ГОСТах.
- Расчетное – получается после вычислений в конкретном проекте.
Первый вариант скорее теоретический, для практических задач используется второй.
Пути увеличения прочностных характеристик
Есть несколько способов это сделать, два основных:
- добавка примесей;
- термообработка, например, закал.
Иногда они используются вместе.
Общие сведения о сталях
Все они обладают химическими свойствами и механическими. Ниже подробнее поговорим о способах увеличения прочности, но для начала представим схему, на которой представлены все разновидности:
Также посмотрим более подробное видео:
Все они обладают химическими свойствами и механическими. Ниже подробнее поговорим о способах увеличения прочности, но для начала представим схему, на которой представлены все разновидности:
Углерод
Чем больше углеродность вещества, тем выше твердость и меньше пластичность. Но в составе не должно быть более 1% химического компонента, так как большее количество приводит к обратному эффекту.
Марганец
Очень полезная добавка, но при массовой доле не более двух процентов. Обычно Mn добавляют для улучшения качеств обрабатываемости. Материал становится более подвержен ковке и свариванию. Это объясняется вытеснением кислорода и серы.
Кремний
Эффективно повышает прочностные характеристики, при этом не затрагивая пластичность. Максимальное содержание – 0,6%, иногда достаточно и 0,1%. Хорошо сочетается с другими примесями, в совокупности можно увеличить устойчивость к коррозии.
Азот и кислород
Если они попадают в сплав, но ухудшают его характеристики, при изготовлении от них пытаются избавиться.
Легирующие добавки
Также можно встретить следующие примеси:
- Хром – увеличивает твёрдость.
- Молибден – защищает от ржавчины.
- Ванадий – для упругости.
- Никель – хорошо влияет на прокаливаемость, но может привести к хрупкости.
Эти и другие химические вещества должны применяться в строгих пропорциях в соответствии с формулами. В статье мы рассказали про предел прочности (кратковременное сопротивление) – что это, и как с ним работать. Также дали несколько таблиц, которым можно пользоваться при работе. В качестве завершения, давайте посмотрим видеоролик:
Чтобы уточнить интересующую вас информацию, свяжитесь с нашими менеджерами по телефонам 8 (908) 135-59-82; (473) 239-65-79; 8 (800) 707-53-38. Они ответят на все ваши вопросы.
Источник
1. Механические характеристики
Надёжность работы электрических машин, аппаратов и установок зависит от качества и правильного выбора соответствующих электротехнических материалов. При рациональном выборе электротехнических материалов можно создать электрооборудование малых габаритов и массы, надёжное в эксплуатации. Но для этого необходимо знать свойства электротехнических материалов и их изменения под воздействием электрического напряжения, температуры и других факторов.
Величины, с помощью которых оценивают те или иные свойства материалов, называют характеристиками. Чтобы полностью оценить свойства того или иного электротехнического материала, необходимо знать его механические, электрические, тепловые и физико-химические характеристики. У магнитных материалов – магнитные.
К основным механическим характеристикам материала относятся:
- Разрушающее напряжение при растяжении δр,
- Разрушающее напряжение присжатии δс,
- Разрушающее напряжение при статическом изгибе δи,
- Ударная вязкость а
Разрушающее напряжение при растяжении δропределяют на образцах материала определенной формы, при которой обеспечивается равномерное распределение растягивающего усилия по площади сечения в средней части образца. Образец 2 утолщёнными концами закрепляют в стальных зажимах (захватах) 1 испытательной машины (рис). Нижний зажим машины неподвижен, а к другому прикладывают разрушающее (растягивающее) усилие Рр, которое плавно нарастает с определённой скоростью до момента разрыва образца.
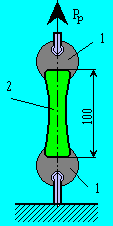
Видео об испытании механических характеристик
Рассчитывается по формуле: δр = (Мпа)
где Р – разрушающее усилие при разрыве образца, Н; S площадь поперечного сечения образца до испытания, м2.
Разрушающее напряжение при сжатии δс, определяется на образцах, имеющих форму цилиндра или куба. Так, у формованных и прессованных пластмасс эта характеристика определяется на образцах, представляющих собой сплошные цилиндры высотой 15 мм и диаметром 10 мм.
Образец располагают между стальными плитами испытательного пресса, к которым прикладывают сжимающую нагрузку. Последнюю повышают с определенной скоростью до момента разрушения образца.
Рассчитывается по формуле: δc = (Мпа)
где Р – разрушающее усилие при разрыве образца, Н; S площадь поперечного сечения образца до испытания, м2.
Разрушающее напряжение при статическом изгибе δи определяется на образцах, представляющих собой бруски прямоугольного сечения. Образец 2 материала (рис) помещают в испытательную машину, где он своими концами свободно опирается на две стальные опоры 3. Изгибающее усилие Ри прикладываемое к середине образца 2 через стальной наконечник 1, плавно увеличивают и доводят до величины, при которой происходит разрушение образца.
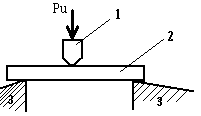
Рассчитывается по формуле: δи = 1,5 Ри L / (b h)2 (Мпа)
где Ри – изгибающее усилие, Н; L – расстояние между стальными опорами в испытательной машине, м; b и h – ширина и толщина образца м.
Ударная вязкость — α –характеризуется способностью материала сопротивляться ударным нагрузкам и определяется отношением работы ∆А, затраченной на разрушение образца, к площади его первоначального сечения Sо:
α = ∆ А/ Sо (Дж/м2)
Чем меньше ударная вязкость, тем более хрупок данный материал.
Источник
При растяжении и сжатии в сечении действует только нормальное напряжение. Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади. Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис.32.).
Исходя из гипотезы плоских сечений, можно предположить, что напряжение при растяжении и сжатии в пределах каждого сечения не меняются. По этому напряжение можно рассчитать по формуле:
где Nz — продольная сила; А — площадь поперечного сечения.
Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения (рис. 33а), а при сжатии к сечению (рис. 336).
Размерность (единица измерения) напряжений — (Па), однако это слишком малая единица, и практически напряжения рассчитывают в
При определении напряжений брус разбивают На участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений. Рассчитывают напряжения по сечениям, и расчёт оформляют в виде эпюры нормальных напряжений.
Строится и оформляется такая же эпюра, как и эпюра продольных сил.
Пусть в результате деформации первоначальная длина стержня l станет равной. l1. Изменение длины
называется абсолютным удлинением стержня.
Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением ( – эпсилон) или продольной деформацией. Продольная деформация – это безразмерная величина. Формула безразмерной деформации:
При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.
Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:
.
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона иликоэффициентом поперечной деформации, вычисляется по формуле:
Для различных материалов коэффициент Пуассона изменяется в пределах . Например, для пробки , для каучука , для стали , для золота .
5. Определение перемещений в стержне при растяжении-сжатии.
При растяжении — сжатии относительная продольная деформация в каждой
точке поперечного сечения стержня одна и та же и определяется как
где и — продольное перемещение поперечного сечения. Из
данного равенства du = zdx. Интегрируя его
(10)
где м0 — перемещение начального поперечного сечения стержня; и — перемещение рассматриваемого поперечного сечения, положение которого определяется координатой х ; л:0- координата начального поперечного сечения.
По закону Гука при растяжении-сжатии где Е — модуль упругости
1-го рода материала стержня. Обозначим — изменение длины
стержня для рассматриваемого поперечного сечения. Тогда (10) примет вид
Если свойства материала по длине стержня не изменяются и Е const, то
. (12)
Функция нормальных напряжений а, как правило, имеет разрывы при переходе с одного участка на другой (рис.7,6) и непрерывна в пределах каждого участка. Поэтому, если рассматриваемое сечение (рис. 7,в) находится в пределах первого участка 0<х<а (0<Jtj < я), то изменение длины стержня
в данном поперечном сечении равно (учитываем, что а, = const)
Если рассматриваемое сечение (рис. 7,г) находится в пределах 2-го участка , то изменение длины стержня в данном поперечном сечении равно (учитываем, что ст2 ~ const)
(14)
6. Диаграмма растяжения и механические характеристики материала.
Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.
Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).
Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.
Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
На рис. 1 показана диаграмма для малоуглеродистой стали. Она построена в системе координат F-Δl, где:
F — продольная растягивающая сила, [Н];
Δl — абсолютное удлинение рабочей части образца, [мм]
Рис. 1 Диаграмма растяжения стального образца
Как видно из рисунка, диаграмма имеет четыре характерных участка:
I — участок пропорциональности;
II — участок текучести;
III — участок самоупрочнения;
IV — участок разрушения.
Рассмотрим подробнее процесс построения диаграммы.
В самом начале испытания на растяжение, растягивающая сила F, а следовательно, и деформация Δl стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О).
На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня Δl растут пропорционально увеличивающейся нагрузке F.
После прохождения точки А диаграмма резко меняет свое направление и на участке II начинающемся в точке B линия какое-то время идет практически параллельно оси Δl, то есть деформации стержня увеличиваются при практически одном и том же значении нагрузки.
В этот момент в металле образца начинают происходить необратимые изменения. Перестраивается кристаллическая решетка металла. При этом наблюдается эффект его самоупрочнения.
После повышения прочности материала образца, диаграмма снова «идет вверх» (участок III) и в точке D растягивающее усилие достигает максимального значения. В этот момент в рабочей части испытуемого образца появляется локальное утоньшение (рис. 2), так называемая «шейка», вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).
Рис. 2 Стальной образец с «шейкой»
Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения образца, растягиваещее усилие необходимое для его растяжения уменьшается, и кривая диаграммы «идет вниз».
В точке E происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована «шейка»
Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:
W=0,8Fmax⋅Δlmax
По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.
Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.
7.
8. Понятия о допускаемых напряжениях и деформациях при растяжении и сжатии. Условия прочности и жёсткости. Три вида расчетов на прочность и жесткость.
Допускаемые напряжения – это наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы.
Как показывают механические испытания (испытания на растяжение и сжатие), разрушение хрупких материалов начинается, когда напряжения в сечении элемента конструкции превысят величину временного сопротивления (предела прочности) σв. Поэтому для хрупких материалов, деформация которых, как правило, незначительна, за опасное (предельное) напряжение следует принимать именно предел прочности σв:
σо = σв.
Для пластичных материалов за опасное (предельное) напряжение следует принимать предел текучести σт (или условный предел текучести σ0,2, если площадка текучести отсутствует), так как за пределом текучести в пластичных материалах возникают значительные пластические деформации, приводящие при сбросе нагрузки до нуля к появлению остаточных напряжений, следовательно:
σо = σт .
Естественно, что эти опасные напряжения не могут быть использованы в качестве допускаемых. Их следует уменьшить настолько, чтобы в эксплуатационных условиях действующие напряжения гарантированно были меньше опасных, а деформации были упругими. Таким образом, допускаемое напряжение может быть определено по формуле σо
где σо – опасное напряжение; n – коэффициент запаса прочности.
Рассмотрим условия прочности и жесткости для случаев простого растяжения (сжатия). Опасность наступления разрушения характеризуется величинами наибольших нормальных и касательных напряжений, возникающих при нагружении в опасных (т. е. наиболее напряженных) точках сечения. Очевидно, что реальные материалы не могут выдерживать сколь угодно большие напряжения. Поэтому величины наибольших напряжений из условия надежности работы детали необходимо ограничивать некоторыми допустимыми значениями, такими, чтобы деталь испытывала только упругие деформации. Их называют допускаемыми напряжениями. При растяжении и сжатии допускаемые напряжения обозначают [σ+], [σ–] соответственно (принято также обозначение σadm).
Если из расчета известны максимальные и минимальные (по алгебраической величине) напряжения, возникающие в опасном сечении детали, то условия прочности могут быть записаны следующим образом:
Если материал одинаково сопротивляется растяжению и сжатию, что характерно для пластичных материалов (более строго–для материалов в пластичном состоянии), а значит [σ+]=[σ–]=[σ], то
иусловие прочности при растяжении (сжатии) запишем в виде:
В некоторых случаях для обеспечения нормальной работы машин и сооружений размеры их деталей нужно выбирать так, чтобы обеспечивалось условие жесткости, то есть ограничить предельные деформации (перемещения) элементов конструкции.
Условие жесткости, ограничивающее изменение длины элемента, имеет следующий общий вид:
где∆l – изменение размеров детали; [∆l] – допускаемая величина этого изменения.
Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин ∆l по участкам
условие жесткости при растяжении (сжатии) запишем следующим образом:
Используя условие прочности, можно решать три типа задач:
1) проектировочный расчет – по известным нагрузкам для известного материала найти надежные с точки зрения прочности размеры поперечного сечения стержня (спроектировать прочную деталь);
2) проверочный расчет – по заданным размерам и материалу детали проверить, может ли она выдержать приложенную нагрузку;
3) расчет по несущей способности (грузоподъемности) – по известным размерам детали, материалу и схеме нагружения определить допустимую величину нагрузки на деталь.
9. Напряжения и деформации при сдвиге. Условие прочности.
Сдвиг (срез) – вид деформации, при котором одна часть стержня смещается относительно другой (скользит). Сдвиг, как вид нагружения, встречается редко и имеет место в заклепочных и сварных соединениях. Деформация сдвига происходит в случае, если к стержню приложены две равные по модулю противоположно направленные силы P , перпендикулярные к его продольной оси. Расстояние между этими силами должно быть малым, чтобы можно было пренебречь моментом, создаваемым силами.
Рис. 16. Расчетная схема при сдвиге
Используя метод сечений (разрезая стержень между силами P), можно установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная сила Q.
Такой вид нагружения, при котором в поперечных сечениях стержня действует только поперечная сила, называют чистым сдвигом.
Мера скольжения одного поперечного сечения относительно другого – касательные напряжения τ.
Принято, что касательные напряжения распределены по всей площади поперечного сечения равномерно. Если в поперечном сечении стержня площадью A возникает внутренняя поперечная сила Q = P, то касательные напряжения в любой точке этого сечения будут равны: T = Q/A = P/A.
Рис. 17. Чистый сдвиг
При чистом сдвиге возникает плоское напряженное состояние, тогда напряжения, действующие на площадке составляющей угол α с вертикальной исходной площадкой равны:
Касательные напряжения τ, приведенные на рис. 17, по абсолютной величине больше касательных напряжений по любым другим площадкам. Таким образом, они являются экстремальными, а площадки, по которым они действуют – площадками сдвига. Так как по этим площадкам не действуют нормальные напряжения, то их называют площадками чистого сдвига и они образуют с главными площадками углы, равные 45°.
При чистом сдвиге нормальные напряжения на любых двух взаимно перпендикулярных площадках равны друг другу по модулю и противоположны по направлению.
Касательные напряжения τ измеряются в таких же единицах, что и нормальные напряжения: мегапаскалях, килоньютонах на квадратные сантиметры, килограммах силы на квадратный сантиметр (МПа, кН/см2, кгс/см2) и т.п.
В результате сдвига одно поперечное сечение стержня смещается относительно другого на величину δ, называемую абсолютным сдвигом.
Рис. 18. Углы сдвига
10. Напряженное состояние и закон гука при сдвиге
Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения , где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: s1= — s3 = t; s2= 0. Главные площадки составляют с площадками чистого сдвига угол 45о.
При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. d — абсолютный сдвиг,
g » — относительный сдвиг или угол сдвига.
Закон Гука при сдвиге: g = t/G или t = G×g .
G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, m— коэффициент Пуассона).
Потенциальная энергия при сдвиге: .
Удельная потенциальная энергия деформации при сдвиге: ,
где V=а×F — объем элемента. Учитывая закон Гука, .
Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.
11. Определение напряжений при кручении круглых валов. Условие прочности.
Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряженийи записывается в виде
где — берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:
— из второй теории прочности
— из теории Мора
Из теорий прочности для пластичных материалов при чистом сдвиге получим:
— по третьей теории прочности
— по четвертой теории прочности
Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором , то при повороте граней элемента на 450 в новых площадках обнаруживаются только нормальные напряжения, равные по величине (рис.5.8).
Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис.5.9,а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 450, т.е. по направлению действия максимальных растягивающих напряжений (рис.5.9,б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис.5.9,в).
Рис.5.8 Рис.5.9
Таким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равным — для хрупких материалов и — для пластичных материалов.
12. Определение угла закручивания круглых валов. Условие жесткости.
При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения.
Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T. Затем из условий равновесия остановленной части вала определяют крутящий момент:
T = Мк= Σ Мi . (5.1)
Таким образом, крутящий момент в каком-либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.
Рис. 5.1
Угол сдвига
Максимальное касательное напряжение
Деформации вала
Угол закручивания:
— относительный
— абсолютный
Условие жесткости вала
Расчет вала при кручении сводится к одновременному удовлетворению двух условий:
— условия жесткости:
13. Полярный момент инерции и полярный момент сопротивления для круглого сечения вала.
Геометрические характеристики круглых сплошных сечений вала:
Поля́рный моме́нт ине́рции — интегральная сумма произведений площадей элементарных площадок dA на квадрат расстояния их от полюса — ρ2 (в полярной системе координат), взятая по всей площади сечения. То есть:
— полярный момент инерции
— полярный момент сопротивления
Эта величина используется для прогнозирования способности объекта оказывать сопротивление кручению. Она имеет размерность единиц длины в четвёртой степени (м4, см4) и может быть лишь положительной.
Сама формула выглядит следующим образом:
Для круглого сплошного сечения:
где D — диаметр круга.
Дата добавления: 2016-11-12; просмотров: 7840 | Нарушение авторских прав | Изречения для студентов
Читайте также:
Рекомендуемый контект:
Поиск на сайте:
© 2015-2020 lektsii.org — Контакты — Последнее добавление
Источник
