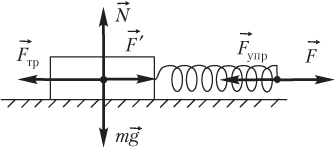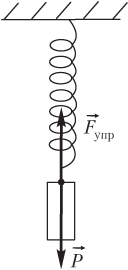Для растяжения недеформированной пружины

2.2. Силы

2.2.5. Сила упругости

Силы упругости возникают при деформации тел.

Вычисление силы упругости производится по закону Гука:

Fупр = k∆x,

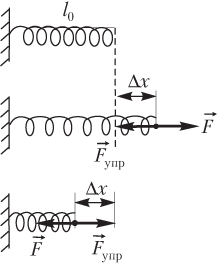
где k — коэффициент жесткости (упругости) пружины; Δx=|l−l0| — абсолютная деформация (растяжения или сжатия) пружины, l0 — длина пружины в недеформированном состоянии, l — длина растянутой (или сжатой) пружины.

Направление силы упругости F→упр (рис. 2.9) противоположно направлению силы, вызывающей деформацию:

F→упр=−F→.

Рис. 2.9

Относительная деформация определяется отношением:

ε=Δxl0 или ε=Δxl0⋅100 %,

где Δx=|l−l0| — абсолютная деформация (растяжения или сжатия) пружины, l0 — длина недеформированной пружины, l — длина растянутой (сжатой) пружины.

Коэффициент жесткости (упругости) k нескольких пружин одинаковой длины, но разной жесткости вычисляется для последовательного соединения по формуле (рис. 2.10)

1k=1k1+1k2+…+1kN;

где k1, k2, …, kN — коэффициенты жесткости (упругости) этих пружин.

Рис. 2.10

Коэффициент жесткости (упругости) k нескольких пружин одинаковой длины, но разной жесткости (рис. 10), вычисляется для параллельного соединения по формуле (рис. 2.11)

k = k1 + k2 + … + kN,

где k1, k2, …, kN — коэффициенты жесткости (упругости) этих пружин.

Рис. 2.11

Для вычисления результирующих коэффициентов жесткости (упругости) параллельного и последовательного соединения одинаковых пружин удобно пользоваться формулами:

• для последовательного соединения N одинаковых пружин с коэффициентами жесткости (упругости) k0:

  k=k0N;

• для параллельного соединения N одинаковых пружин с коэффициентами жесткости (упругости) k0:

  k = k0N.

Пример 16. При последовательном соединении трех пружин, коэффициенты жесткости которых относятся как 1 : 2 : 3, сила 12 Н вызвала растяжение системы на 4,0 см. Рассчитать коэффициенты жесткости указанных пружин.

Решение. Величина силы упругости, действующей на пружину, определяется формулой

Fупр = kобщ∆x,

где kобщ — коэффициент жесткости составной пружины; ∆x — указанное в условии задачи растяжение пружины.

Величина силы упругости, с другой стороны, совпадает с величиной приложенной силы:

Fупр = F.

Значение данной силы и величина растяжения пружины под действием этой силы позволяют рассчитать коэффициент жесткости составной пружины:

kобщ=FΔx=124,0⋅10−2=300 Н/м.

Для определения коэффициентов жесткости каждой пружины запишем их коэффициенты жесткости в следующем виде:

• для первой пружины

k1 = k;

• для второй пружины

k2 = 2k;

• для третьей пружины

k3 = 3k,

так как указанные коэффициенты по условию задачи соотносятся между собой как

k1 : k2 : k3 = 1 : 2 : 3.

Для расчета величины k запишем формулу для коэффициента жесткости пружины, состоящей из трех последовательно соединенных пружин, и подставим в нее выражения k1, k2, k3:

1kобщ=1k1+1k2+1k3=1k+12k+13k=116k, или kобщ=6k11.

Найденное ранее значение kобщ = 300 Н/м позволяет рассчитать k = 550 Н/м.

Тогда коэффициенты жесткости каждой из пружин имеют значения:

• для первой пружины

k1 = k = 550 Н/м;

• для второй пружины

k2 = 2k = 1100 Н/м;

• для третьей пружины

k3 = 3k = 1650 Н/м.

Пример 17. Вычислить абсолютную деформацию пружины с коэффициентом жесткости 100 Н/м, присоединенной к бруску, лежащему на горизонтальной поверхности, в момент начала скольжения бруска по поверхности. Сила, вызывающая скольжение бруска, прикладывается к пружине. Коэффициент трения между бруском и поверхностью равен 0,1. Масса бруска составляет 1,0 кг.

Решение. На рисунке показаны силы, действующие на брусок.

Абсолютную деформацию пружины рассчитаем по формуле

Δx=Fупрk,

где Fупр = F — модуль силы упругости, возникающей в пружине (величина силы упругости равна величине приложенной силы); k — коэффициент жесткости пружины.

Со стороны пружины на брусок действует сила, модуль которой совпадает с силой упругости:

F′=Fупр=F.

В момент начала скольжения величина силы трения равна силе, приложенной к бруску в направлении движения:

Fтр=F′=μN,

где µ — коэффициент трения; N = mg — модуль силы нормальной реакции опоры.

Поэтому величина силы упругости может быть вычислена по формуле

Fупр = µmg.

Из исходного уравнения следует, что величина деформации пружины в момент начала скольжения определяется выражением

Δx=μmgk.

Расчет позволяет определить ее значение:

Δx=0,1⋅1,0⋅10100=10−2 м=1,0 см.

Пример 18. Вычислить массу груза, подвешенного к пружине жесткостью 250 Н/м, если известно, что относительная деформация пружины составляет 25 %. Длину нерастянутой пружины считать равной 100 мм.

Решение. Проиллюстрируем условие задачи рисунком.

Сила упругости определяется формулой

Fупр = k∆x,

где k — коэффициент жесткости (упругости) пружины; ∆x = l − l0 — абсолютная деформация пружины (величина ее растяжения под действием груза); l0 — длина недеформированной пружины; l — длина пружины в деформированном состоянии.

Из определения относительной деформации

ε=Δxl0

следует, что

∆x = εl0,

где ε = 0,25 — относительная деформация (в долях).

С учетом значения относительной деформации формула для вычисления силы упругости принимает вид:

Fупр=kεl0=0,25kl0.

С другой стороны, сила упругости, возникающая в пружине, численно равна весу тела, вызвавшего деформацию пружины:

Fупр = P = mg,

где m — масса тела; g — модуль ускорения свободного падения.

Таким образом, имеем равенство

0,25kl0 = mg,

позволяющее вычислить массу груза, подвешенного к пружине:

m=0,25kl0g=0,25⋅250⋅0,10010=0,625 кг=625 г.