Диаграмма растяжения зуб текучести

Текучесть — свойство тел пластически или вязко деформироваться под действием напряжений.

Основой современной теории тезкой текучести, которую еще нельзя считать окончательно установившейся, является все то же положение, выдвинутое Коттреллом: зуб и площадка текучести обусловлены резким увеличением числа подвижных дислокаций в начале пластического течения. Это значит, что для их появления требуется выполнение двух условий: 1) в исходном образце число свободных дислокаций должно быть очень малым, и 2) оно должно иметь возможность быстро увеличиться по тому или иному механизму в самом начале пластической деформации.

Если продеформировать железный образец, например до точки, разгрузить его и тут же вновь растянуть, то зуба и площадки текучести не возникнет, потому что после предварительного растяжения в новом исходном состоянии образец содержал множество подвижных, свободных от примесных атмосфер дислокаций. Если теперь после разгрузки от точки А образец выдержать при комнатной или слегка повышенной температуре, т.е. дать время для конденсации примесей на дислокациях, то при новом растяжении на диаграмме опять появится зуб и площадка текучести. Необходима конденсация примесей на дислокациях, тогда снова получим зуб текучести.

Теория площадки и зуба текучести

Образование зуба и площадки текучести (так называемое явление резкой текучести) внешне выглядит следующим образом. Упругое растяжение приводит к плавному подъему сопротивления деформированию вплоть до σт.в , затем происходит относительно резкий спад напряжений до σт.н и последующая деформация (обычно на 0,1-1 %) идет при неизменном внешнем усилии – образуется площадка текучести. Во время удлинения, соответствующего этой площадке, образец на рабочей длине покрывается характерными полосами Чернова – Людерса, в которых локализуется деформация. Поэтому величину удлинения на площадке текучести (0,1 – 1%) часто называют деформацией Чернова – Людерса.

Упрочнение при торможении дислокаций

Дислокации связаны атмосферами (распределением атомов вокруг дислокации), которые не могут следовать за дислокацией. Для отрыва дислокации от атмосферы требуется сила, большая, чем для ее движения. Следовательно, если дислокация «заторможена» атмосферами, то для дальнейшей деформации нужно создать большее напряжение. Это ведет к образованию «зуба текучести» и упрочнению металла.

Так же: упрочнение происходит при увеличении плотности дислокаций на границах зерен, до их отрыва и движения

Дислокация — линейный дефект, образующий внутри кристалла зону сдвига. Бывает краевая (линейный сдвиг кристалла) и винтовая (сдвиг кристалла по плоскости).

Лекция 8

Кратко рассмотрим, какие основные стадии накопления повреждений свойственны периоду зарождения трещин при кратковременном статическом деформировании.

Первая стадия — стадия микротекучести. Это стадия простирается от начала нагружения до возникновения первых линий скольжения на площадке текучести. На этой стадии определяются такие характеристики как предел пропорциональности и предел упругости. Несмотря на то, что остаточная макродеформации на этой стадии практически равна нулю, в металле протекает микропластическая деформация, причем наиболее интенсивно в приповерхностных слоях металла глубиной порядка размера зерна. Это связано с тем, что в приповерхностных слоях металла в благоприятно ориентированных зернах пластическое течение начинается раньше, чем во внутренних объемах металла. Причина такого поведения связана с рядом факторов: особенностью закрепления приповерхностных источников дислокации (имеющих одну точку закрепления), у которых критическое напряжение начала их работы значительно ниже, чем у источников в объеме; наличием в поверхностном слое более грубой, чем в объеме, дислокационной сетки Франка и в этом случае для генерирования дислокаций требуется меньшее напряжение; наличием поверхностных концентраторов напряжения; различием скоростей движения дислокаций у поверхности и внутри металла и рядом других факторов. Внутри металла на этой стадии наблюдается движение отдельных дислокаций и локальный процесс размножения дислокаций в благоприятно ориентированных зернах, преимущественно в области границ зерен. Для металлических материалов с физическим пределом текучести окончание этой стадии четко фиксируется началом негомогенной деформации Людерса-Чернова.

Вторая стадия — стадия текучести, на которой наблюдается негомогенная деформация в виде прохождения по всей рабочей зоне образца фронта Людерса — Чернова. В металлах, проявляющих площадку текучести при статическом растяжении, гетерогенная деформация на площадке текучести, происходящая путем лавинообразного распространения пластического течения, связана с быстрым размножением дислокаций на линии продвигающегося фронта деформации. Плотность дислокаций в этой зоне возрастает от исходной в отожженном материале (107 – 108 см-2) до величины порядка 1010 см-2. Позади фронта деформации средняя плотность дислокаций остается затем практически постоянной в течении всего времени деформации на площадке текучести и начинает увеличиваться вновь лишь с последующим ростом напряжений по окончании стадии текучести и перехода в стадию деформационного упрочнения. Основным источником возникновения новых дислокаций на фронте текучести являются границы зерен и другие поверхности раздела. Степень пластической деформации поликристаллических металлов на площадке текучести неоднородна и зависит от ориентации отдельных зерен. В наиболее деформированных зернах уже действует множественное скольжение и возникает дислокационная структура с признаками ячеистой.

И на этой стадии эволюция дислокационной структуры также более существенна в приповерхностных слоях металла и области границ зерен. С точки зрения синергетического подхода резкий физический предел текучести можно рассматривать как точку бифуркации, а сам переход от упругой деформации к пластической, как аналог неравновесного фазового перехода II рода, хотя есть мнение, что при процессах пластической деформации и разрушения проявляются особенности фазовых переходов обоих типов.

В основе современной теории площадки текучести и зуба текучести лежит идея Коттрелла о резком увеличении числа подвижных дислокаций в начале пластического течения. Для этого требуется два условия: 1) в исходном образце число подвижных дислокаций должно быть очень малым; 2) оно должно иметь возможность быстро увеличиваться. Резко увеличится число подвижных дислокаций может за счет следующих факторов: а) разблокировки дислокаций от атмосфер: б) образования новых дислокаций; в) размножения дислокаций при их взаимодействии. Было показано, что появление площадки текучести на кривых деформирования металлических материалов может быть также объяснено барьерным эффектом приповерхностного слоя. Более прочный приповерхностный слой может быть создан предварительно путем поверхностного упрочнения или сформироваться в непосредственно в процессе пластической деформации за счет опережающего пластического течения приповерхностных слоев в металлических материалах.

Третья стадия — стадия деформационного упрочнения. На этой стадии в металлах продолжается увеличиваться плотность дислокаций в условиях сдвигообразования по нескольким плоскостям скольжения и формируется дислокационная ячеистая структура с критической плотностью дислокаций 1013 …1014 см-2 (рис 2.7, в). Эта дислокационная структура является диссипативной и ее образование связано с термодинамической неустойчивостью системы в точке бифуркации, когда, например, хаотичная структура перейдет на новый более дифференцированный и более высокий уровень упорядоченности или организации. Кульман — Вильсдорф такие структуры называет низкоэнергетическими дислокационными структурами, для которых характерно наличие объемов, практически свободных от дислокаций, с граничными областями, в которых плотность дислокаций очень высока. Следует отметить, что уже в самом начале стадии деформационного упрочнения в локальных объемах металла формируется области с критической плотностью дислокаций, в которых после определенной степени пластической деформации зарождаются субмикротрещины порядка 100 нм. И. А. Одингом и Ю. П. Либеровым на этой стадии было обнаружено критическое напряжение, при котором на поверхности металла появляются субмикротрещины размером 1-2 мкм. Близкий по физическому смыслу критерий рассмотрен в работах Л. М. Рыбаковой и Б. А. Прусакова, однако кривая растяжения в этом случае строится в координатах S — 5 с определением истинных напряжения и деформации. При этом кривая растяжения выглядит в виде линейных участков с разным углом наклона.

Описанная выше периодичность и стадийность разрушения при кратковременном статическом растяжении характерна для пластичных металлических материалов. Естественно, что в зависимости от структурного состояния материалов и условий деформирования (высокие и низкие температуры, скорость деформирования, окружающая среда) характер разрушения может изменяться, однако сохраняются общие закономерности стадийности накоплений повреждений.

Лекция 9

Источник

собе пластического течения для сохранения непрерывности деформации поликристалла на границах необходимы или корреляция между формоизменением соседних зерен, или приспособление деформации в приграничных зонах.

Уже в монокристаллах имеет место стесненность деформации вследствие трения на поверхностях, соприкасающихся с инструментом, при помощи которого осуществляется деформирование. В условиях осевого нагружения стесненность приводит к развитию плоского течения монокристаллов всех ориентаций, за исключением тех, для которых осевая симметрия формоизменения обусловлена активностью симметрично расположенных систем с равными приведенными напряжениями сдвига. В поликристалле в случае отсутствия корреляции в ориентировке соседних зерен трение на их границах будет приводить к изменению механизма деформации приграничных зон от моноскольжения к множественному скольжению или дополнительному двойникованию для сохранения непрерывности деформации. В этом случае деформация по Заксу будет характерной не для всего объема материала, а только для внутренней части зерен. Такой вариант развития деформации и отражает схема Кохендорфера, показанная на рис. 11.27. Эта схема представляется наиболее физичной и в наибольшей мере отвечает действительности, хотя расчет кривой деформации поликристалла на

ееоснове наименее однозначен.

Вряде случаев на кривых напряжение – деформация наблюдается так называемый зуб текучести, состоящий в увеличении напряжения выше предела текучести (называемого в таких случаях

нижним пределом текучести σнт ) и в последующем его резком падении до σнт (рис. 11.28). При этом наибольшую достигнутую величину напряжения называют верхним пределом текучести σвт .

Образование зуба текучести связывают с резким увеличением числа подвижных дислокаций в начале пластического течения. Зуб текучести появляется всякий раз, когда исходная плотность сво-

бодных дислокаций мала, но в процессе пластической деформации происходит резкое увеличение этой плотности. Скорость пластической деформации ε&p определяется общим числом N подвижных

дислокаций с вектором Бюргерса b в единице объема кристалла и

скоростью движения дислокаций v, т.е.	(11.69)
εp = M N b v ,	(11.69)
&

где М – ориентационный фактор.

Рис. 11.28. Схема явления течения на кривой напряжение–деформация:

1 – первичное нагружение;

2 – повторное нагружение после разгрузки и деформационного старения

Исходное число подвижных дислокаций, или их длина в единице объема, могут быть недостаточны для обеспечения заданной скорости деформации в следующих случаях:

1)плотность дислокаций ρ в первоначально совершенном кристалле мала;

2)хотя общая плотность дислокаций ρ велика, число подвижных дислокаций недостаточно, тогда как большинство их заблокировано атмосферами примесных атомов;

3)скорость движения дислокаций v, зависящая от величины сдвигового напряжения, при данной величине напряжения слишком мала.

Впервом случае пластическая деформация интенсифицируется, когда сдвиговое напряжение станет достаточным для активизации дислокационных источников Франка–Рида; подобное поведение наблюдается у нитевидных металлических кристаллов. Во втором случае зуб текучести появляется в результате или разблокирования дислокаций, когда напряжение оказывается достаточным для отрыва их от примесных атомов, или в результате образования новых

Диаграмма растяжения зуб текучести

дислокаций, если первоначальное закрепление дислокаций оказывается слишком сильным. По имеющимся данным, количество подвижных дислокаций N из числа возникающих в процессе пластической деформации равно N ≈ 0,1 ρ. В третьем случае зуб текучести появляется в результате размножения дислокаций, позволяющего уменьшить скорость их движения и, соответственно, величину напряжения, необходимого для осуществления деформации с заданной скоростью. Чтобы поддерживать данную скорость деформации, N дислокаций должны двигаться со скоростью v, но если количество дислокаций возрастает до 2N, то требуемая скорость их движения будет равна только v/2. Если теперь принять во внимание, что меньшей скорости движения дислокаций соответствует более низкое напряжение, то на кривой напряжение – деформация при увеличении числа подвижных дислокаций должно наблюдаться падение напряжения.

Обозначив плотности подвижных дислокаций на верхнем и нижнем пределах текучести как ρв и ρн, а скорости их движения vв и vн, получаем:

vв / vн = ρн / ρв .

(11.70)

Рис. 11.29. Кривые напряжение–деформация, рассчитанные в предположении различной зависимости скорости дислокаций от напряжения

Диаграмма растяжения зуб текучести

Зависимость скорости движения дислокаций v от сдвигового

напряжения τ подчиняется соотношению:
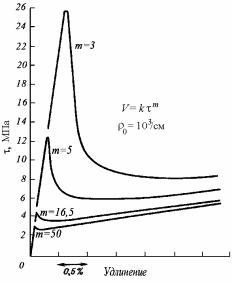
v = k τm ,	(11.71)
где m может изменяться от 1 до 100. Следовательно:
τв / τн = (ρн /ρв)1/m.	(11.72)

Отсюда следует, что как m, так и ρв являются критериями величины зуба текучести. При малых значениях m отношение τв /τн будет большим, соответствуя сильно выраженному зубу текучести, тогда как при значениях m, близких к 50, зуб текучести едва различим

(рис. 11.29).

В ряде случаев обнаруживаются повторяющиеся зубцы текучести (или так назывемая пилообразная деформация), рассматривае-

мые как проявление эффекта Портевена–Ле-Шателье (рис.

11.30).

Рис. 11.30. Эффект Портевена– Ле Шателье, обнаруживаемый, например, при растяжении поликристаллических алюминиевых сплавов

Этот эффект – следствие динамической неустойчивости, поскольку он наблюдается тогда, когда коэффициент упрочнения dσ/dε уменьшается при увеличении скорости деформирования. Серия ступенек на кривой свидетельствует о том, что напряжение или/и скорость деформации непрерывно колеблются между двумя крайними значениями. По-видимому, перемещение дислокаций также изменяется от медленного до быстрого и обратно. Во время медленной фазы скорость пластической деформации мала и напряжение растет. В конце концов, оно становится достаточным для того, чтобы высвободить дислокации, и тогда наступает фаза быстрого пластического течения, распространяющегося по образцу в виде пластической волны. Во время этой фазы напряжение падает, движение дислокаций замедляется и цикл вновь повторяется. Ввиду по-

вторяющегося ступенчатого характера поднимающейся кривой на- пряжение–деформация очевидно, что цикл определяется не абсолютным значением напряжения, а значением, относящимся к мгновенному напряжению течения, которое непрерывно изменяется.

11.3.16. Влияние температуры на деформацию поликристаллов

Температура оказывает чрезвычайно сильное влияние на форму кривых напряжение–деформация поликристаллов. С понижением температуры деформации верхний предел текучести заметно возрастает, перепад между вершиной зуба текучести и площадкой текучести, а также протяженность этой площадки постепенно увеличиваются. Уменьшение критического скалывающего напряжения τкр и уровня напряжений течения на стадии I кривой напряжение– деформация – общее явление для металлов с разными решетками. Снижение τкр наиболее существенно в области низких температур. Например, повышение температуры испытания Mg от 100 до 300 К приводит к двукратному снижению τкр, в то время как дальнейшее повышение температуры до 600 К уже почти не сказывается на величине τкр. При низких температурах дислокации, имеющиеся в образце, прочно блокированы конденсированными на них атмосферами примесных атомов внедрения, тогда как с повышением температуры подвижность примесных атомов существенно возрастает и блокировка дислокаций ослабляется.

Увеличение доли стадии III в пластической деформации и снижении коэффициента упрочнения на этой стадии с повышением температуры обусловлены облегчением поперечного скольжения дислокаций. Чем выше температура деформации, тем больше вероятность термической активации заторможенных у барьеров дислокаций и преодоления ими этих барьеров. Чем легче идет поперечное скольжение при самых низких температурах, тем меньше влияние нагрева на dσ/dε.

В общем случае расхождение кривых напряжение–деформация при разных температурах (рис. 11.31) обусловлено двумя причинами:

Диаграмма растяжения зуб текучести

Рис. 11.31. Влияние снижения температуры испытания на кривые деформационного упрочнения

1) различием субструктур, возникающих при разных температурах испытания;

2) зависимостью напряжения течения от температуры (при одинаковой субструктуре).

Предположим, что действует лишь причина 2. Тогда, если после прекращения деформации при Т2 в точке В мгновенно снизить температуру до Т1, то напряжение течения скачком повысится до значения

D, и при дальнейшей деформации кривая пойдет так же, как если бы с самого начала образец растягивали при Т1.

Если расхождение кривых связано только с разницей в субструктурах, то после снижения температуры от Т2 до Т1 в точке В изменится лишь наклон кривой: дальнейшему растяжению при Т1 соответствует пунктир ВK, причем кривая ВK не параллельна кривой ОDЕ, так как исходные субструктуры в точках В и D разные. Очевидно, что при действии обеих рассматриваемых причин имеет место какой-то промежуточный вариант – например, CL. Относительный вклад каждой из причин количественно оценивается соотношением (σС/σB)/(B σD/σBB), которое можно определить экспериментально. Чем ближе это отношение к единице, тем более значительно влияние температурной зависимости напряжения течения.

Экспериментально показано, что для чистых металлов температурная зависимость сопротивления деформации незначительна, а главной причиной влияния температуры на напряжение течения и коэффициент упрочнения является разница в субструктурах, формирующихся при разных температурах испытания. Например, у Al и Cu отношение σС/σBB близко к единице (1,1 – 1,4), а (σС/σB)/(B σD/σB)B = 0,5 ÷ 0,67. При этом для ГЦК металлов действует

правило Коттрела–Стокса:

Δσ /σ = const, (11.73)

где Δσ – изменение напряжения течения, вызванное мгновенным изменением температуры деформации, равное (σС – σB),B а σ – начальное (σB) или конечное (σС) напряжение.

Подъем температуры испытания выше (0,2–0,25) Тпл приводит к тому, что в ходе деформации более или менее полно успевают проходить процессы динамического возврата. При этом картина пластической деформации значительно изменяется. Динамический возврат, как и статический возврат, проходящий при отжиге после деформации, состоит в устранении избытка точечных дефектов и в перестройке дислокационной структуры, формирующейся при деформации. Такая перестройка возможна лишь в условиях активного протекания термически активируемых процессов – поперечного скольжения и, особенно, переползания дислокаций. Чем выше температура, тем полнее протекание возврата.

При высокотемпературной деформации перемещение дислокаций происходит под одновременным действием внешних напряжений и температурного воздействия (в отличие от возврата при отжиге после деформации). Здесь дислокации уже не привязаны так жестко к своей плоскости скольжения, как при низкотемпературной деформации, и могут легко переходить из одной плоскости в другую, выбирая себе самый легкий путь. При таком движении дислокаций увеличивается вероятность их встреч и поэтому, с одной стороны, растет число случаев их аннигиляции, вызывающих уменьшение плотности дислокаций, а с другой стороны – усиливается склонность к образованию регулярных дислокационных структур, для которых характерно объединение большинства дислокаций в малоугловые границы. Таким образом, в процессе деформации при повышенных температурах деформационное упрочнение из-за повышения плотности дислокаций и увеличения эффективности их торможения будет конкурировать с разупрочнением из-за снижения плотности дислокаций и совершенствования дислокационной структуры в результате возврата.

Диапазон температур по гомологической шкале от 0,2–0,25 до 1 делится на два интервала, граница между которыми соответствует

(0,5–0,6) Тпл. Между (0,2–0,25) и (0,5–0,6) Тпл идет так называемая

теплая деформация, а выше (0,5–0,6) Тпл – горячая деформация. В

процессе теплой деформации возврат всегда неполный, то есть число вновь образующихся дислокаций больше, чем число аннигилирующих. Поэтому при теплой деформации, как и при холодной,

Источник