Диаграмма растяжения твердого тела
>>> Перейти на мобильный размер сайта >>>
Учебник для 10 класса
ФИЗИКА
- Чтобы, строить надежные здания, мосты, станки, разнообразные машины, необходимо знать механические свойства используемых материалов: дерева, бетона, стали, железобетона, пластмасс и т. п. Конструктор должен заранее знать поведение материалов при значительных деформациях, условия, при которых материалы начнут разрушаться. Сведения о механических свойствах различных материалов получают в основном экспериментально.
- В этом параграфе мы рассмотрим механические свойства твердых тел на примере исследования деформации растяжения, так как обычно испытание материалов проводят именно на растяжение и сжатие. Для этого нам необходимо ввести еще одно важное понятие.
Напряжение
В любом сечении деформируемого тела действуют силы упругости, препятствующие разрыву тела на части (рис. 9.15). Деформированное тело находится в напряженном состоянии, которое характеризуется особой величиной, называемой механическим напряжением или короче — напряжением.
Рис. 9.15
Напряжение — величина, равная отношению модуля силы упругости к площади поперечного сечения(1) тела:
где σ — напряжение, Fynp — модуль силы упругости и S — площадь поперечного сечения.
В СИ за единицу напряжения принимается паскаль (Па):
1 Па = 1 Н/м2.
Заметим, что в формуле (9.3.1) иногда удобно модуль силы упругости заменить на модуль F внешней деформирующей силы, уравновешивающей силу упругости.
Диаграмма растяжения
Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств (например, с помощью гидравлического пресса) подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения с от относительного удлинения е. Этот график называют диаграммой растяжения (рис. 9.16).

Рис. 9.16
Закон Гука
Многочисленные опыты показывают, что при малых деформациях напряжение а прямо пропорционально относительному удлинению ε (участок ОА диаграммы). Эта зависимость называется законом Гука. Его можно записать так:
Относительное удлинение в формуле (9.3.2) взято по модулю, так как закон Гука справедлив как для деформации растяжения, так и для деформации сжатия, когда ε < 0 (рис. 9.17).

Рис. 9.17
Коэффициент пропорциональности Е, входящий в закон Гука, называется модулем упругости или модулем Юнга.
Если относительное удлинение ε = 1, то σ = Е. Следовательно, модуль Юнга равен напряжению, возникающему в стержне при его относительном удлинении, равном единице. Так как ε = , то при ε = 1 Δl = l0. А это значит, что модуль Юнга равен напряжению, возникающему в стержне при удвоении длины образца. Практически любое тело (кроме резины) при упругой деформации не может удвоить свою длину: значительно раньше оно разорвется. Поэтому модуль Юнга определяют по формуле (9.3.2), измеряя напряжение о и относительное удлинение е при малых деформациях.
Из формулы (9.3.2) видно, что единица модуля Юнга в СИ такая же, как и единица напряжения, т. е. паскаль.
Чем больше модуль упругости Е, тем меньше деформируется стержень при прочих равных условиях (l0, S, F). Таким образом, модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения или сжатия.
Закон Гука, записанный в форме (9.3.2), легко привести к виду (9.3.1).
Действительно, подставив в (9.3.2) получим:
Откуда
Обозначим
тогда
Таким образом, согласно (9.3.4) жесткость k стержня прямо пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.
Пределы пропорциональности и упругости
Эксперимент показывает, что малые деформации полностью исчезают после снятия нагрузки (упругая деформация). При малых деформациях выполняется закон Гука. Максимальное напряжение, при котором еще выполняется закон Гука, называется пределом пропорциональности.
Если продолжать увеличивать нагрузку при растяжении и превзойти предел пропорциональности, то деформация становится нелинейной (линия ABCDEK, рис. 9.16). Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участок АВ графика). Максимальное напряжение, при котором еще не возникают заметные остаточные деформации, называется пределом упругости σуп. Он соответствует точке В графика. Предел упругости превышает предел пропорциональности не более чем на 0,33%. В большинстве случаев их можно считать равными.
Предел и запас прочности
Если внешняя нагрузка такова, что в теле возникают напряжения, превышающие предел упругости, то характер деформации меняется (участок BCDEK графика, рис. 9.16). После снятия нагрузки образец не принимает прежние размеры, а остается деформированным, хотя и с меньшим удлинением, чем при нагрузке (пластическая деформация).
За пределом упругости при некотором значении напряжения, соответствующем точке С графика (см. рис. 9.16), удлинение возрастает практически без увеличения нагрузки (участок CD диаграммы почти горизонтален). Это явление называется текучестью материала.
При дальнейшем увеличении нагрузки напряжение повышается (от точки D), после чего в наименее прочной части образца появляется сужение («шейка»). Из-за уменьшения площади сечения (точка Е) для дальнейшего удлинения нужно меньшее напряжение, но в конце концов наступает разрушение образца (точка К). Наибольшее напряжение, которое выдерживает образец без разрушения, называется пределом прочности. Обозначим его σпч (оно соответствует точке Е диаграммы). Его значение сильно зависит от природы материала и его обработки.
Чтобы свести к минимуму возможность разрушения сооружения, инженер должен при расчетах допускать в его элементах такие напряжения, которые будут составлять лишь часть предела прочности материала. Их называют допустимыми напряжениями. Число, показывающее, во сколько раз предел прочности больше допустимого напряжения, называют коэффициентом запаса прочности.
Обозначив запас прочности через n, получим:
Запас прочности выбирается в зависимости от многих причин: качества материала, характера нагрузки (статическая или изменяющаяся со временем), степени опасности, возникающей при разрушении, и т. д. На практике запас прочности колеблется от 1,7 до 10. Выбрав правильно запас прочности, инженер может определить допустимое в конструкции напряжение.
Закон Гука для деформации сдвига
При деформации сдвига сила направлена по касательной к плоскости верхней грани тела (см. рис. 9.8J. Эта сила уравновешивается возникающей силой упругости: = -упр Отношение модуля силы упругости, возникающей при деформации сдвига, к площади верхней грани называется касательным напряжением и обозначается буквой τ:
Опыт показывает, что касательное напряжение х при малых деформациях прямо пропорционально углу сдвига а. Это и есть закон Гука для деформации сдвига. Он записывается так:
Коэффициент у называется модулем сдвига. Он численно равен касательному напряжению при угле сдвига в 1 рад. Очевидно, что для абсолютного большинства реальных материалов такое напряжение нельзя приложить к реальным телам, не разрушая их.
В СИ единицей модуля сдвига является 1 Па/рад.
Наиболее полную информацию об упругих свойствах материалов дает диаграмма растяжения, получаемая экспериментально. При малых деформациях напряжение в твердом теле прямо пропорционально относительной деформации (закон Гуна).
(1) Сечение тела производится плоскостью, перпендикулярной направлению силы упругости. При этом предполагается, что деформация тела во всех участках сечения одинакова.
Источник
Чтобы строить надежные дома, мосты, станки, разнообразные машины, необходимо знать механические свойства используемых материалов: бетона, стали, железобетона, пластмасс и т. д. Конструктор должен заранее знать поведение материалов при значительных деформациях, условия, при которых материалы начнут разрушаться. Сведения о механических свойствах различных материалов получают экспериментально.
В этом параграфе мы рассмотрим механические свойства твердого тела на примере исследования деформации растяжения. Но предварительно введем еще одно важное понятие.
Напряжение. В любом сечении деформированного тела действуют силы упругости, препятствующие разрыву тела на части (рис. 88). Состояние деформированного тела характеризуют особой величиной, называемой напряжением или, точнее, механическим напряжением. Напряжение — величина, равная отношению модуля силы упругости к площади поперечного сечения тела:
В СИ за единицу напряжения принимается .
Диаграмма растяжения. Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения о от относительного удлинения получивший название диаграммы растяжения (рис. 89).
Закон Гука. Опыт показывает, что при малых деформациях напряжение о прямо пропорционально относительному удлинению (участок ОА диаграммы). Эта зависимость, называемая законом Гука, записывается так:
Относительное удлиненнее в формуле (7.2) взято по модулю, так как закон Гука справедлив как для деформации растяжения, так и для деформации сжатия, когда
Рис. 88
Рис. 89
Коэффициент пропорциональности Е, входящий в закон Гука, называется модулем упругости или модулем Юнга.
Если относительное удлинение то Следовательно, модуль Юнга равен напряжению, возникающему в стержне при его относительном удлинении, равном 1. Так как то при А это значит, что модуль Юнга равен напряжению, возникающему при удвоении длины образца. Практически любое тело при упругой деформации не может удвоить свою длину; значительно раньше любой стержень разорвется. Поэтому модуль Юнга определяют по формуле (7.2), измеряя напряженнее и относительное удлинение при малых деформациях.
Для большинства широко распространенных материалов модуль Юнга определен экспериментально. Так, для хромоникелевой стали Па, а для алюминия Па. Чем больше Е, тем меньше деформируется стержень при прочих равных условиях (одинаковых Модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения (сжатия).
Закон Гука, записанный в форме (7.2), легко привести к виду, известному из курса физики VIII класса.
Действительно, подставив в получим:
Отсюда
Обозначим тогда
Таким образом, жесткость стержня прямо пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.
Пределы пропорциональности и упругости. Мы уже говорили, что закон Гука выполняется при небольших деформациях, а следовательно, при напряжениях, не превосходящих некоторого предела. Максимальное напряжение при котором еще выполняется закон Гука, называют пределом пропорциональности.
Если увеличивать нагрузку, то деформация становится нелинейной: напряжение перестает быть прямо пропорциональным относительному удлинению. Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участок диаграммы). Максимальное напряжение, при котором еще не возникают заметные остаточные деформации (относительная остаточная деформация не превышает называют пределом упругости Предел
упругости превышает предел пропорциональности лишь на сотые доли процента.
Предел прочности. Если внешняя нагрузка такова, что напряжение в материале превышает предел упругости, то после снятия нагрузки образец хотя и укорачивается, но не принимает прежних размеров, а остается деформированным.
По мере увеличения нагрузки деформация нарастает все быстрее и быстрее. При некотором значении напряжения, соответствующем на диаграмме точке С, удлинение нарастает практически без увеличения нагрузки. Это явление называют текучестью материала (участок CD). Кривая на диаграмме идет при этом почти горизонтально.
Далее с увеличением деформации кривая напряжений начинает немного возрастать и достигает максимума в точке Е Затем напряжение быстро спадает и образец разрушается (точка К). Таким образом, разрыв происходит после того, как напряжение достигает максимального значения называемого пределом прочности (образен растягивается без увеличения внешней нагрузки вплоть до разрушения). Эта величина зависит от материала образца и его обработки.
Источник
Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.
Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).
Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.
Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
На рис. 1 показана диаграмма для малоуглеродистой стали. Она построена в системе координат F-Δl, где:
F — продольная растягивающая сила, [Н];
Δl — абсолютное удлинение рабочей части образца, [мм]

Рис. 1 Диаграмма растяжения стального образца
Как видно из рисунка, диаграмма имеет четыре характерных участка:
I — участок пропорциональности;
II — участок текучести;
III — участок самоупрочнения;
IV — участок разрушения.
Построение диаграммы
Рассмотрим подробнее процесс построения диаграммы.
В самом начале испытания на растяжение, растягивающая сила F, а следовательно, и деформация Δl стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О).
На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня Δl растут пропорционально увеличивающейся нагрузке F.
После прохождения точки А диаграмма резко меняет свое направление и на участке II начинающемся в точке B линия какое-то время идет практически параллельно оси Δl, то есть деформации стержня увеличиваются при практически одном и том же значении нагрузки.
В этот момент в металле образца начинают происходить необратимые изменения. Перестраивается кристаллическая решетка металла. При этом наблюдается эффект его самоупрочнения.
После повышения прочности материала образца, диаграмма снова «идет вверх» (участок III) и в точке D растягивающее усилие достигает максимального значения. В этот момент в рабочей части испытуемого образца появляется локальное утоньшение (рис. 2), так называемая «шейка», вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).
Рис. 2 Стальной образец с «шейкой»
Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения образца, растягиваещее усилие необходимое для его растяжения уменьшается, и кривая диаграммы «идет вниз».
В точке E происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована «шейка»
Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:
W=0,8Fmax∙Δlmax
По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.
Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.
Предел пропорциональности >
Примеры решения задач >
Лабораторные работы >
Источник
Механические свойства твердых тел. Диаграмма растяжения
Необходимые сведения о механических свойствах различных материалов получают экспериментально.
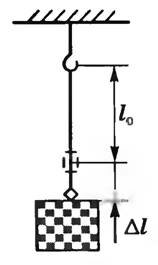
Рис. 1
Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств подвергают растяжению (рис. 1), измеряют удлинение образца и возникающее в нем напряжение. На основании данных опыта строят график зависимости напряжения от относительного удлинения, называемый диаграммой растяжения. Диаграмма растяжения изображена на рисунке 2. При небольших напряжениях (линейный участок OA) относительное удлинение прямо пропорционально напряжению, т.е. выполняется закон Гука. При дальнейшем увеличении напряжения деформация еще остается упругой, но ее зависимость от напряжения перестает быть линейной (участок АВ).
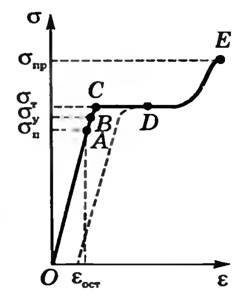
Рис. 2
Наибольшее напряжение σп, при котором справедлив закон Гука, называют пределом пропорциональности.
Наибольшее напряжение σу, при котором деформация еще остается упругой, называется пределом упругости.
При напряжениях, превышающих предел упругости, образец после снятия нагрузки не восстанавливает свою форму (пунктирная кривая). Это пластические деформации. Мерой остаточной деформации служит отрезок εост.
В области пластической деформации (участок CD) деформация происходит почти без увеличения напряжения. Это явление называется текучестью. Напряжение σт, при котором материал течет, называют пределом текучести. Материалы, у которых область текучести CD значительна, могут без разрушения выдерживать большие деформации. Если же область текучести материала почти отсутствует, он без разрушения сможет выдерживать лишь небольшие деформации. Материал, который разрушается при небольших деформациях, называют хрупким (стекло, фарфор, чугун, бетон).
Для дальнейшего увеличения деформации необходимо снова увеличить напряжение (участок DE). После точки Ε кривая идет вниз и дальнейшая деформация вплоть до разрыва происходит при все меньших напряжениях. Наибольшее напряжение σпр, которое способен выдержать образец без разрушения, называют пределом прочности.
Способность материала сопротивляться разрушению и остаточной деформации, возникающим в результате внешних воздействий, называют прочностью материала.
Знание величин σу, σт, σпр материалов важно для использования их в промышленности и строительстве.
При конструировании машин и сооружений нельзя рассчитывать на их работу в условиях, когда испытываемые ими напряжения близки к пределу прочности материала, из которого они сделаны, так как это всегда будет создавать опасность разрушений. На практике допустимое напряжение выбирают так, чтобы оно составляло лишь некоторую часть предела прочности.
Число, показывающее, во сколько раз предел прочности σпр превосходит допустимое (фактически действующее) напряжение, называют запасом прочности (коэффициентом безопасности) n:
n = σпр / σд .
Для повышения прочности материалов их подвергают термической обработке и обработке давлением или вводят в них упрочняющие примеси (легирование).
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 192-193.
Источник
