Диаграмма растяжения допускаемое напряжение
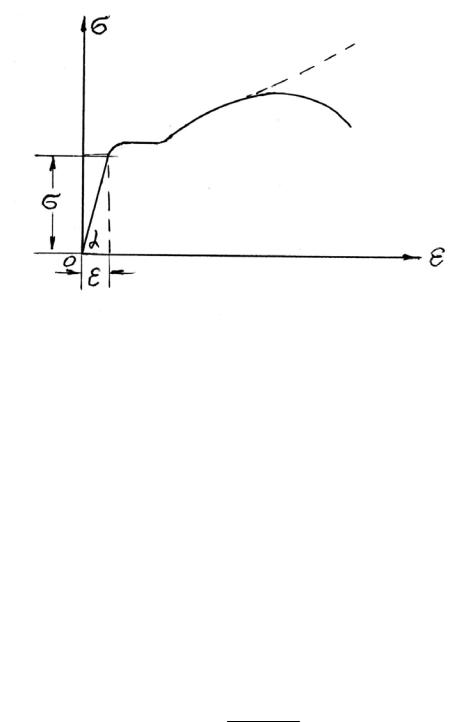
Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.
Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).
Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.
Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
На рис. 1 показана диаграмма для малоуглеродистой стали. Она построена в системе координат F-Δl, где:
F — продольная растягивающая сила, [Н];
Δl — абсолютное удлинение рабочей части образца, [мм]

Рис. 1 Диаграмма растяжения стального образца
Как видно из рисунка, диаграмма имеет четыре характерных участка:
I — участок пропорциональности;
II — участок текучести;
III — участок самоупрочнения;
IV — участок разрушения.
Построение диаграммы
Рассмотрим подробнее процесс построения диаграммы.
В самом начале испытания на растяжение, растягивающая сила F, а следовательно, и деформация Δl стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О).
На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня Δl растут пропорционально увеличивающейся нагрузке F.
После прохождения точки А диаграмма резко меняет свое направление и на участке II начинающемся в точке B линия какое-то время идет практически параллельно оси Δl, то есть деформации стержня увеличиваются при практически одном и том же значении нагрузки.
В этот момент в металле образца начинают происходить необратимые изменения. Перестраивается кристаллическая решетка металла. При этом наблюдается эффект его самоупрочнения.
После повышения прочности материала образца, диаграмма снова «идет вверх» (участок III) и в точке D растягивающее усилие достигает максимального значения. В этот момент в рабочей части испытуемого образца появляется локальное утоньшение (рис. 2), так называемая «шейка», вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).

Рис. 2 Стальной образец с «шейкой»
Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения образца, растягиваещее усилие необходимое для его растяжения уменьшается, и кривая диаграммы «идет вниз».
В точке E происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована «шейка»
Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:
W=0,8Fmax∙Δlmax
По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.
Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.
Предел пропорциональности >
Примеры решения задач >
Лабораторные работы >
Источник
В ходе опыта на растяжение был получен график зависимости удлинения от приложенной силы.
Позже были введены относительные величины, такие как напряжение и относительное удлинение. Благодаря этим величинам можно модифицировать исходный график из опыта так, что по нему сразу можно будет определить необходимые величины, безотносительно того, какую геометрию имел образец в опыте.
Однако сделать это можно двумя путями:
- Искать истинные напряжения и истинные относительные удлинения
- Для нахождения напряжений использовать только исходную площадь поперечного сечения; для нахождения относительного удлинения абсолютное удлинение делить на исходную длину недеформированного стержня
Несмотря на то, что первый способ является точным по своей сути, в инженерной практике используют упрощённый подход. Во-первых, для расчётов на прочность ищутся действующие и допускаемые напряжения и затем сравниваются. В случае применения истинной диаграммы для определения допускаемых напряжений, расчётчикам так же пришлось бы вычислять точные площади для определения истинных действующих напряжений, что является неоправданно трудоёмким процессом. Во-вторых, на интересующем линейном участке истинная и упрощённая инженерная диаграммы практически совпадают:
Выше показана диаграмма растяжения для некоторого стального образца: кривая В – истинная диаграмма, кривая A – инженерная диаграмма.
Если применить второй (упрощённый) способ к диаграммам из опыта, то характер кривых не изменится:
Всё это рассказывается потому, что в современной практике люди, делающие расчёты на прочность, при выборе допускаемых напряжений руководствуются НЕ диаграммой растяжения в целом, а лишь некоторыми характерными точками, снятыми с этой диаграммы.
Для каждого металлического материала в дальнейшем будем выделять две характерные точки на оси напряжений:
- Напряжение, выше которого образец будет иметь заметные остаточные деформации
- Напряжение, при котором образец воспринял наибольшую силу
Если взглянуть на график для стали, то можно заметить, что имеется такой участок, на котором начинает значительно расти удлинение, при этом сила практически не меняется. Материал как будто течёт. Назовём этот участок площадкой текучести, а соответствующее напряжение – пределом текучести. Явление текучести материала характерно для строительных сталей, бронзы, латуни. Обозначим это напряжение как σт:
На графике для алюминия такой площадки нет. Тем не менее введём некоторый условный предел, скажем, напряжение, при котором остаточная деформация равняется 0.002 мм/мм или 0.2%. Назовём его условным пределом текучести и обозначим как σ02. Условный предел текучести используется для титановых и алюминиевых сплавов:
Вторая характерная точка – это напряжение, при котором образец выдержал наибольшую силу. Согласно диаграмме растяжения, этому напряжению соответствует начало образования шейки в образце – локализованного уменьшения поперечного сечения. После этого предела сила начинает падать, потому образец продолжил удлиняться. Если же после этого предела растягивающая сила продолжит увеличиваться, то образец разрушится. Этот предел назовём пределом прочности или временным сопротивлением разрушению и будем обозначать σв или σпч:
Также иногда встречается и третья характерная точка – это напряжение, соответствующее окончанию начального линейного участка. Это напряжение называется пределом пропорциональности. Оно чуть меньше предела текучести и, строго говоря, пользоваться нужно именно им, а не пределом текучести. Однако для его определения нужны очень точные измерительные приборы. Потому общепринято пользоваться пределом текучести в качестве предела, выше которого будут значительные остаточные деформации.
Помимо характерных напряжений, имеется также и одна характерная деформация — это относительное удлинение при разрыве. Это отношение абсолютного удлинения образца при разрыве к исходной недеформированной длине. Эту величину чаще всего обозначают греческой буквой δ, её размерность либо мм/мм, либо в %. По этой величине можно судить о степени пластичности того или иного материала.
Примеры того, в каком виде расчётчик получает представления о механических свойствах материала:
Д16 (дюраль)
30ХГСА (легированная сталь)
Источник
8
независимости действия сил. Согласно этому принципу (принцип суперпозиции) конечный результат не зависит от последовательности приложения нагрузки. Экспериментальная проверка результатов расчетов, теории, положенной в их основу, осуществляется замером деформаций на реальных объектах с помощью различных конструкций тензометров [11] и перерасчетом их величин в напряжения согласно закону Гука.
Механические характеристики, или иначе, механические свойства материалов – это показатели прочности, пластичности, упругости, выраженные в определенных числовых значениях. Эти характеристики определяются на основе лабораторных испытаний материалов [1], [15], [17].
Для наиболее распространенных материалов – металлов, их сплавов, а также синтетических и композитных материалов – механические характеристики можно найти в справочной литературе [9], [10], [11] и др.
Однако эти характеристики могут существенно меняться в зависимости от технологической обработки, условий производства и т.д.
В связи с этим на предприятиях часто возникает необходимость уточнения их величин, выявления соответствия того или иного материала стандарту.
Основным методом испытаний, дающим наибольший объем информации о свойствах материалов, является испытание на растяжение до момента разрушения. Испытания проводятся на образцах типа цилиндрических или пла-
стинчатых стержней с отношением длины к диаметру (к ширине пластины) 10:1
или 5:1. Подробное описание процесса испытания и обработки результатов приведены в методических указаниях по проведению лабораторных работ [1],
[13]и в ГОСТ 1497 – 84.
Впроцессе испытания разрывная машина выполняет запись диаграммы зависимости продольной деформации стержня (образца) от нагрузки в коорди-
9
натах Р– ∆l . Эта диаграмма является записью внешнего проявления физиче-
ских процессов, происходящих в материале в процессе нагружения [1], [13], [26] и др.
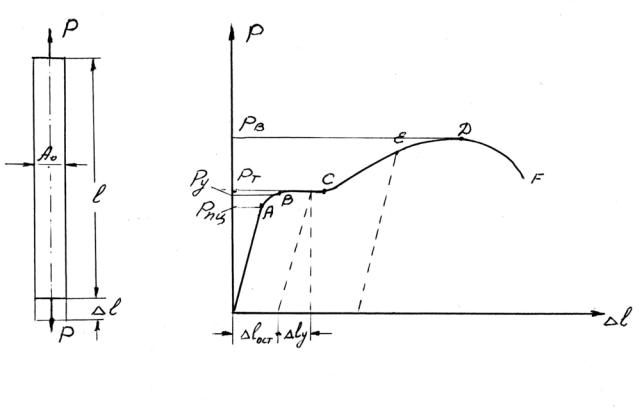
Рассмотрим эту диаграмму (рис.3).
Рис.3 При нагружении стержня растягивающей силой происходит приращение
длины стержня – ∆l . Это удлинение носит название абсолютной продольной деформации.
На участке ОА диаграммы деформация растет пропорционально росту нагрузки; на этом участке диаграммы отражается только упругая работа материала. При снятии нагрузки с образца в этот период деформация сразу исчезает.
Сила, отвечающая точке А диаграммы, где пропорциональность между силой и деформацией заканчивается, называется силой, соответствующей пре-
делу пропорциональности – Pпц .
На участке АВ диаграммы материал стержня еще упруго сопротивляется внешней нагрузке, но пропорциональность между Р и ∆l уже нарушается. Си-
ла, отвечающая точке В диаграммы, называется силой, соответствующей пре-
делу упругости – Ру .
ост.
10
От точки В диаграммы деформация стержня растет почти при постоянном значении нагрузки. В материале на этом этапе нагружения происходит пластическая деформация, сопровождающаяся наклепом – упрочнением с потерей пластичности. На участке ВС диаграммы материал как бы «течет». Этот участок диаграммы носит название площадки текучести.
Если на этом участке, как и на любом последующем, после точки В, например, в точке F или в точке Е разгрузить образец, то он уже не возвращает свои первоначальные размеры. Он получает остаточную пластическую дефор-
мацию ∆l , хотя упругие свойства он не теряет и на участке CD их даже
увеличивает.
Таким образом, после точки В диаграммы полное удлинение образца – его продольная абсолютная деформация, состоит из двух деформаций:
∆l = ∆lост. + ∆lупр. .
Сила, отвечающая точке С, после которой дальнейшее увеличение ∆l
идет с ростом нагрузки, называется силой, соответствующей пределу те-
кучести Рт.
То обстоятельство, что материал после площадки текучести не теряет своей упругости, используется в строительной практике и в отдельных случаях, в машиностроении.
Так, проволока для тросов, проводов, арматура для железобетонных конструкций, звенья якорных цепей и др., чтобы они в процессе работы не вытягивались, а заодно и увеличилась их упругость, подвергаются предварительному наклепу вытяжкой или холодной прокаткой. Наклеп может быть снят, если это необходимо, отжигом.
Площадь диаграммы ω, произведение Р ×∆l – работа, затраченная на разрушение. Очевидно, чем она больше, тем лучше материал будет сопротивляться действию внешних сил, в том числе ударным нагрузкам.
Наивысшая точка диаграммы D свидетельствует о начале разрушения образца. В этот момент сечение стержня образца резко уменьшается с образова-нием так
11
называемой «шейки»; нагрузка начинает падать и образец разрывается (точка
К).
Сила, отвечающая точке D, называется силой, соответствующей вре-
менному сопротивлению материала – Рв . Для многих сплавов, в том числе для высокопрочных легированных сталей, площадка текучести бывает выражена очень слабо. Силы Py и Pт практически не различимы. В этом случае силу, со-
ответствующую пределу текучести, принимают при величине деформации, равной 0,2% от первоначальной длины стержня. Эту силу называют силой, со-
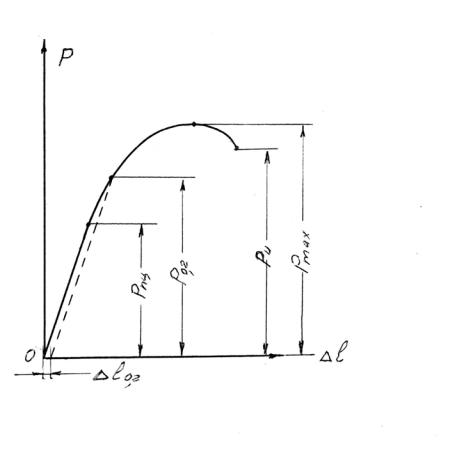
ответствующей условному пределу текучести – Р0,2 (рис.4).
Рис.4
Диаграмма растяжения ∆l = f (P) характеризует свойства конкретного образца, имеющего определенные размеры. Чтобы говорить о свойствах материала и чтобы можно было сравнивать результаты испытаний на разных образцах и на разных машинах, полученная диаграмма перестраивается в координа-
тах напряжение – относительная деформация σ = P / A0 ; ε = ∆l / l0 (рис.5).
Втакой диаграмме:
σnц = Рпц / A0 – предел пропорциональности;

12
σy = Рy / A0 – предел упругости;
σт = Рт / A0 – предел текучести;
σв = Рв / A0 – предел временного сопротивления;
σ0,2 = Р0,2 / A0 – условный предел текучести.
Рис.5 Полученные значения напряжений – пределы являются важнейшими ха-
рактеристиками механических свойств материалов.
Для материалов, у которых площадка текучести отсутствует, наибольшее значение силы на диаграмме (в точке D) называется силой, соот-
ветствующей пределу прочности Pпч , а напряжение σпч = Рпч / A0 – предел прочности.
Материалы, имеющие такую диаграмму, относятся к хрупким (находящимся в хрупком состоянии).
Характеристиками пластичности материала являются:
– относительное остаточное удлинение δ% (после разрыва образца)
δ = l разр. −l0 100% .
l0

13
ψ = A0 − Aразр. 100% .
А0
Для конструкционных углеродных сталей δ = 8 − 27%, ψ до 70%.
При работе машин, сооружений нельзя допустить, чтобы под действием нагрузки какие-либо детали получали остаточные пластические деформации или разрушались. Это значит, что при всех обстоятельствах реальные напряжения должны соответствовать условиям работы материала в пределах упругости и быть ниже, чем σпц . Поэтому предельные напряжения: σпц ; σу ; σт – для уп-
ругопластичного материала являются опасными – σ0 . Для хрупкого материала
опасным напряжением является | σпч. . |
Величины σпц ; σу ; σт | не очень разнятся по своим значениям, и если |
принять в качестве «коэффициента запаса» число n ≥1,5 , то, разделив любые из опасных пределов на «п», получим напряжение, безопасное для работы материала. Это напряжение называется допускаемым:
[σ]= σ0 / n .
Очевидно, что условие работы – температура, характер нагрузки (статическая или ударная), агрессивность внешней среды, степень ответственности самой конструкции и т.д. должны быть учтены в расчетах. Поэтому коэффициент запаса не берется произвольно, а принимается по нормативным документам соответствующих отраслей промышленности [6], [14], [25] и др. Многие значения коэффициентов запаса можно найти в справочниках [6], [18], и по величине они могут быть 8-10 и более.
Зная величину допускаемого напряжения, можно записать условие прочности для деталей, работающих на растяжение – сжатие
σ = P ≤ [σ].
A0
Это условие справедливо для материалов, в равной степени хорошо сопротивляющихся растяжению и сжатию. Для хрупких материалов таких, как чугун, бетон, камень и др., которые хорошо работают на сжатие и плохо вы-

E = (0,7 − 0,72) 105 МПа ;
E =1,95 105 МПа ;
14
держивают растягивающую нагрузку, должно быть записано два условия прочности
σраст. = РрастА . ≤ [σ]раст.
σсж. = РАсж. ≤ [σ]сж. ,
где [σ] | = | Рпч( раст.) | = | σ0 ( раст.) | ; | [σ] | = | Рпч(сж.) | = | σ0 (сж.) | ; п – коэффици- |
раст. | |||||||||||
А п | п | сж. | А п | п | |||||||
ент запаса.
В сопротивлении материалов принято считать сжимающую нагрузку, напряжения и деформацию со знаком минус (–). Все, что относится к растяжению – со знаком плюс ( + ).
Кроме характеристик прочности и пластичности важными характеристиками материалов являются показатели упругих свойств. Такими показателями являются: модуль продольной упругости Е Мпа и коэффициент Пуассона µ. Модуль продольной упругости – коэффициент пропорциональности между напряжением и деформацией в законе Гука:
σ = ε E .
Закон Гука, который можно охарактеризовать так: «Чем больше сила (напряжение), тем больше деформация», связывает воедино два этих понятия в пределах упругой работы материала. Величина Е для каждого материала имеет свое постоянное значение. Из зависимости между σ и ε в законе Гука следует,
что величина модуля упругости Е может быть найдена из диаграммы ε = f (σ),
как tg α (см. рис.5) E = σ/ ε.
Для конструкционных углеродистых сталей модуль упругости принима-
ется: E = 2,1 105 МПа ;
для высокопрочных легированных сталей:
для меди: E =1 105 МПа ;
для сплавов алюминия:
Источник
Экспериментальные изучения свойств материалов
В результате эксперимента определяются параметры характеризующие физ. (υ,Е) и мех.(σупр,σпропор,σтекуч, σвремен) свойства материалов. Физ. свойства не зависят от напряженного состояния образца (растяжение, изгиб, кручение), а механические зависят. Всех эти величины мы определяем по диаграмме. Для начала чертим диаграмму в координатах «сила- удлинение». Но для изучения свойств материала значительно удобнее иметь диаграммы, построенные в координатах «напряжение – относительная деформация» (рис- ниже).

Пока растягивающие напряжения не достигают некоторой величины σПЦ., диаграмма представляет собой прямую линию, т.е. относительные удлинения Е прямопропорциональны удлинением σ; то есть, до этого предела справедлив закон Гука. Напряжение σПЦ. называется пределом пропорциональности.
σПЦ.=FПЦ./А0
А0-первоначальная (до деформации) площадь поперечного сечения образца. FПЦ.– максимальная сила, до которой F пропорционально ΔF.
После достижения условия пропорциональности следует участок- криволинейный, на котором присутствует предел упругости.
σУПР.=FУпр./А0
FУПР.- максимальная сила до которой сохраняются упругие силы образца.
Предел упругости- напряжение до которого сохраняются упругие свойства материала, тесть остаточная деформация при разгрузке не обнаруживается.
Начиная с момента, когда напряжения достигнуть некоторой величины σТ., деформации растут без увеличения напряжений, тоесть без значительного увеличения силы, и на диаграмме получается участок, параллельный оси абсцисс. Это явление наз. текучестью материала, а напряжение σТ.- пределом текучести. Участок диаграммы, параллельный оси абсцисс, наз. площадкой текучести.
σТ.=FT./A0
FT.- минимальная сила при которой начинает течь материал.
При дальнейшем растяжении образца напряжения, выдерживаемое образцом, наз. пределом прочности, или временным сопротивлением, и обозначается σТ.. Это напряжение соответствует точке 3 диаграммы. Последующее растяжение образца сопровождается уменьшением растягивающей силы. То есть, предел прочности представляет собой отношение наибольшей силы, которую выдерживает образец, к первоначальной площади его поперечного сечения.
σВ.=FMAX./A0
FMAX.-максимальная сила, которую выдерживает материал обраца до разрушения.
После достижения максимальной силы, при дальнейшем растяжении образца деформация происходит, главным образом, на небольшой длине образца. Это ведет к обрзованию местного сужения в виде шейки и к падению силы. Обозначим через FK. Величину растягивающей силы в момент разрыва, получим
σК.=FK./A0
Допускаемое напряжение может быть определено по формуле;
σ МАХ.≤[σ ]
[σ]=σ0/ n
где σ0-опасное напряжение (σТ. – для деталей из пластичного материала, σВР.- для деталей из хрупкого материала)
n- коэффициент запаса прочности, показывающий, во сколько раз допускаемое напряжение меньше опасного.
Выбор величины коэффициента запаса прочности зависит от состояния материала (хруп- кое или пластичное), характера приложения нагрузки (статическая, динамическая, повторно- переменная) и некоторых общих факторов. К этим факторам относятся;
1)неоднородность материала, а, следовательно, различие его механических характеристик в малых образцах и деталях.
2) неточность задания величин внешних нагрузок.
3)приближенность расчетных схем и некоторая приближенность расчетных схем.
Для пластичных материалов в случае статической нагрузки опасным напряжением, следует считать предел текучести, т. е. σ0=σТ., а n=nТ.. Тогда
[σ ]=σ0/n=σТ./nT.
Для хрупких материалов при статической нагрузке опасным напряжением является временное сопротивление и тогда
[σ ]=σ0/n=σВ../nВ.
Принимают, что запас прочности nВ.=2,5 до 3,0
Основная задача сопротивления материалов – обеспечить надежные размеры деталей, подверженных тому или иному силовому, температурному или другому воздействию. Такие размеры можно определить из расчета на прочность и жесткость. Отметим прежде всего, что опасность наступления разрушения характеризуется не столько величинами внутренних усилий и моментов в сечении, сколько величинами нормальных наибольших и касательных напряжений, которые действуют в опасных точках сечения. поэтому величины наибольших напряжений из условия надежности работы детали необходимо ограничивать некоторыми допустимыми напряжениями. Допускаемые напряжения можно обозначать [σ+] – при растяжении, [σ-]-при сжатии
Так допускаемые напряжения можно находить из формул запаса прочности.
Источник
