Диаграмма растяжений арматуры а500с
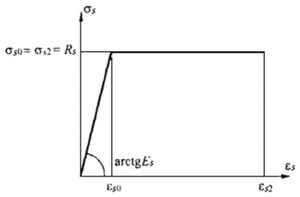
Для примера построения диаграмм взят наиболее часто используемый класс бетона (В25) и арматуры (А500С).
Для расчетов по второму предельному состоянию.
При нормативной длительной нагрузке (для определения прогибов ж/б плит)
Трехлинейная диаграмма
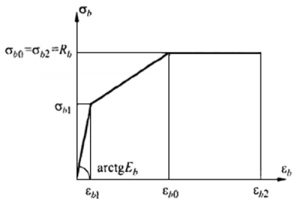
Рис. 1. Трехлинейная диаграмма состояния сжатого бетона из СП 63.13330
СП 63.13330.2012, п. 6.1.25: «При расчете деформаций железобетонных элементов по нелинейной деформационной модели при отсутствии трещин для оценки напряженно-деформированного состояния в сжатом и растянутом бетоне используют трехлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки. При наличии трещин для оценки напряженно-деформированного состояния сжатого бетона помимо указанной выше диаграммы используют, как наиболее простую, двухлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки«.
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb2 = Rb,n = 18,5 МПа.
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
При продолжительном действии нагрузки модуль деформации бетона определяют по формуле:
Eb,t = Eb / 1 + φb,cr = 30000 / 1 + 2,5 = 8571,43 МПа;
Коэффициент φb,cr при нормальной влажности (40-75%) равен 2,5.
При трехлинейной диаграмме значения напряжений σb1 определяют по формуле:
σb1 = 0,6 х Rb,n = 11,1 МПа;
а значения относительных деформаций εb1 принимают:
εb1 = σb1 / Eb,t = 11,1 / 8571,43 = 0,001295.
Значения относительных деформаций εb2 для тяжелого бетона при продолжительном действии нагрузок принимают по таблице 6.10:
εb2 = 0,0048.
Значения предельных относительных деформаций εb0 тяжелого бетона при продолжительном действии нагрузок и нормальной влажности (40-75%) принимают по таблице 6.10:
εb0 = 0,0034.
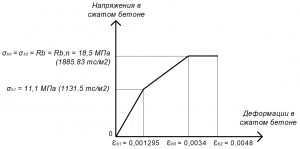
Рис. 2. Трехлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt2 = Rbt,n = 1,55 МПа.
При трехлинейной диаграмме значения напряжений σbt1 определяют по формуле:
σbt1 = 0,6 х Rbt,n = 0,93 МПа;
При продолжительном действии нагрузки модуль деформации бетона определяют по формуле:
Eb,t = Eb / 1 + φb,cr = 30000 / 1 + 2,5 = 8571,43 МПа;
Значения относительных деформаций εbt1 принимают:
εbt1 = σbt1 / Eb,t = 0,93 / 8571,43 = 0,0001085.
Значения предельных относительных деформаций εbt0 тяжелого бетона при продолжительном действии нагрузок и нормальной влажности (40-75%) принимают по таблице 6.10:
εbt0 = 0,00024.
Значения относительных деформаций εbt2 для тяжелого бетона при продолжительном действии нагрузок принимают по таблице 6.10:
εbt2 = 0,00031.
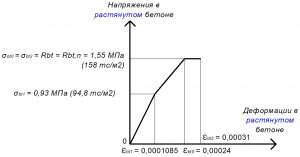
Рис. 3. Трехлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Двухлинейная диаграмма
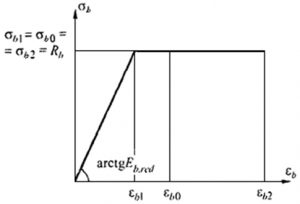
Рис. 4. Двухлинейная диаграмма состояния сжатого бетона из СП 63.13330
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb1 = σb2 = Rb,n = 18,5 МПа.
Значения относительных деформаций εb2 для тяжелого бетона при продолжительном действии нагрузок:
εb2 = 0,0048.
Значения приведенного модуля деформации бетона Eb,red принимают:
Eb,red = Rb,n / εb1,red
Значения относительных деформаций εb1,red принимают по таблице 6.10:
при нормальной влажности (40-75%) εb1,red = 0,0028;
Eb,red = 18,5 / 0,0028 = 6607,14;
εb1 = Rb,n / Eb,red = 18,5 / 6607,14 = 0,0028.
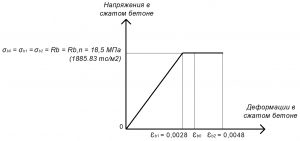
Рис. 5. Двухлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt1 = σbt2 = Rbt,n = 1,55 МПа.
Значения относительных деформаций εbt2 для тяжелого бетона при продолжительном действии нагрузок принимают по таблице 6.10:
εbt2 = 0,00031.
Значения приведенного модуля деформации бетона Ebt,red принимают:
Ebt,red = Rbt,n / εbt1,red
Значения относительных деформаций εbt1,red принимают по таблице 6.10:
при нормальной влажности (40-75%) εbt1,red = 0,00022;
Ebt,red = 1,55 / 0,00022 = 7045,45;
εbt1 = Rbt,n / Ebt,red = 1,55 / 7045,45 = 0,00022.
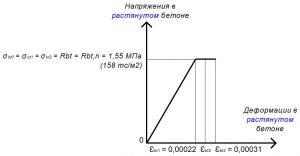
Рис. 6. Двухлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Данные диаграммы построены для бетона при продолжительном действии нагрузок и могут использоваться при расчете прогибов. Для расчета ширины раскрытия трещин нужно строить диаграммы при непродолжительном действии нагрузок, см. п. 6.1.26 СП 63.13330: «При расчете раскрытия нормальных трещин по нелинейной деформационной модели для оценки напряженно-деформированного состояния в сжатом бетоне используют диаграммы состояния, приведенные в 6.1.20 и 6.1.21, с учетом непродолжительного действия нагрузки. При этом в качестве наиболее простой используют двухлинейную диаграмму состояния бетона».
Двухлинейная диаграмма состояния (деформирования) арматуры при нормативной длительной нагрузке

Рис. 7. Двухлинейная диаграмма состояния арматуры из СП 63.13330
Расчетное сопротивление растяжению арматуры Rs:
Rs = σs0 = σs2 = Rs,n = 500 МПа (для А500С).
Значения модуля упругости арматуры принимают одинаковыми при растяжении и сжатии и равными, для арматуры А500С:
Es = 200000 МПа.
Значения относительных деформаций арматуры εs0 принимают равными:
для арматуры с физическим пределом текучести
εs0 = Rs,n / Es = 500 / 200000 = 0,0025.
Значения относительной деформации εs2 принимают равными 0,025.
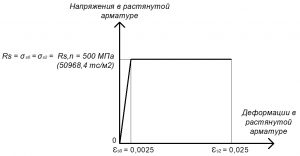
Рис. 8. Двухлинейная диаграмма состояния растянутой (или сжатой) арматуры класса А500С при длительной нормативной нагрузке
При расчете железобетонных элементов по нелинейной деформационной модели в качестве расчетной диаграммы состояния (деформирования) арматуры, устанавливающей связь между напряжениями σs и относительными деформациями εs арматуры, для арматуры с физическим пределом текучести классов А240-А500, В500 принимают двухлинейную диаграмму. Диаграммы состояния арматуры при растяжении и сжатии принимают одинаковыми, с учетом нормируемых расчетных сопротивлений арматуры растяжению и сжатию.
Для расчетов по второму предельному состоянию.
При полной нормативной нагрузке (для проверки ширины раскрытия трещин)
Трехлинейная диаграмма

Рис. 9. Трехлинейная диаграмма состояния сжатого бетона из СП 63.13330
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb2 = Rb,n = 18,5 МПа.
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
При трехлинейной диаграмме значения напряжений σb1 определяют по формуле:
σb1 = 0,6 х Rb = 11,1 МПа;
а значения относительных деформаций εb1 принимают:
εb1 = σb1 / Eb = 11,1 / 30000 = 0,00037.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения предельных относительных деформаций εb0 тяжелого бетона при непродолжительном действии нагрузок:
εb0 = 0,002.
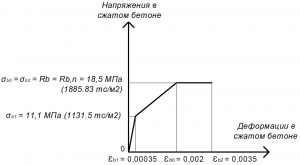
Рис. 10. Трехлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt2 = 1,55 МПа.
При трехлинейной диаграмме значения напряжений σbt1 определяют по формуле:
σbt1 = 0,6 х Rbt = 0,93 МПа;
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
Значения относительных деформаций εbt1 принимают:
εbt1 = σbt1 / Eb = 0,93 / 30000 = 0,000031.
Значения предельных относительных деформаций εbt0 тяжелого бетона при непродолжительном действии нагрузок:
εbt0 = 0,0001.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
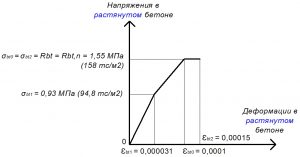
Рис. 11. Трехлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb1 = σb2 = 18,5 МПа.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения приведенного модуля деформации бетона Eb,red принимают:
Eb,red = Rb / εb1,red
Значения относительных деформаций εb1,red принимают при непродолжительном действии нагрузки:
εb1,red = 0,0015;
Eb,red = 18,5 / 0,0015 = 12333,3;
εb1 = Rb / Eb,red = 18,5 / 12333,3 = 0,0015.
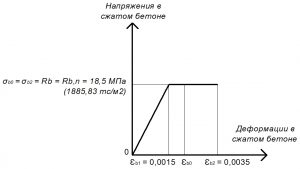
Рис. 12. Двухлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt1 = σbt2 = 1,55 МПа.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
Значения приведенного модуля деформации бетона Ebt,red принимают:
Ebt,red = Rbt / εbt1,red
Значения относительных деформаций εbt1,red принимают при непродолжительном действии нагрузок:
εbt1,red = 0,00008;
Ebt,red = 1,55 / 0,00008 = 19375;
εbt1 = Rbt / Ebt,red = 1,55 / 19375 = 0,00008.
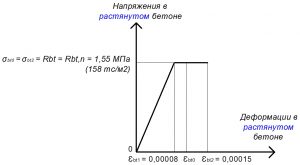
Рис. 13. Двухлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Двухлинейная диаграмма состояния (деформирования) арматуры при полной нормативной нагрузке

Рис. 14. Двухлинейная диаграмма состояния арматуры из СП 63.13330
Расчетное сопротивление растяжению арматуры Rs:
Rs = σs0 = σs2 = 500 МПа (для А500С).
Расчетное сопротивление сжатию арматуры Rs:
Rsс = σsс0 = σsс2 = 500 МПа (для А500С).
Значения модуля упругости арматуры принимают одинаковыми при растяжении и сжатии и равными, для арматуры А500С:
Es = 200000 МПа.
Значения относительных деформаций растянутой арматуры εs0 принимают равными:
для арматуры с физическим пределом текучести
εs0 = Rs / Es = 500 / 200000 = 0,0025.
Значения относительных деформаций сжатой арматуры εsс0 принимают равными:
для арматуры с физическим пределом текучести
εsс0 = Rsс / Es = 500 / 200000 = 0,0025.
Значения относительной деформации εs2 принимают равными 0,025.
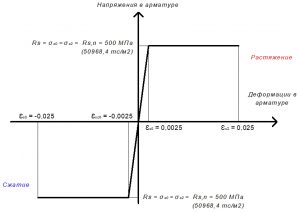
Рис. 15. Двухлинейная диаграмма состояния арматуры класса А500С при полной нормативной нагрузке
Для расчетов по первому предельному состоянию.
При полной расчетной нагрузке (для проверки прочности)
Трехлинейная диаграмма

Рис. 16. Трехлинейная диаграмма состояния сжатого бетона из СП 63.13330
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb2 = 14,5 МПа.
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
При трехлинейной диаграмме значения напряжений σb1 определяют по формуле:
σb1 = 0,6 х Rb = 8,7 МПа;
а значения относительных деформаций εb1 принимают:
εb1 = σb1 / Eb = 8,7 / 30000 = 0,00029.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения предельных относительных деформаций εb0 тяжелого бетона при непродолжительном действии нагрузок:
εb0 = 0,002.
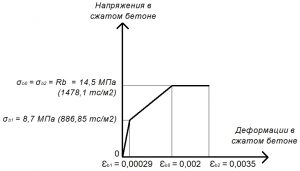
Рис. 17. Трехлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt2 = 1,05 МПа.
При трехлинейной диаграмме значения напряжений σbt1 определяют по формуле:
σbt1 = 0,6 х Rbt = 0,63 МПа;
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
Значения относительных деформаций εbt1 принимают:
εbt1 = σbt1 / Eb = 0,63 / 30000 = 0,000021.
Значения предельных относительных деформаций εbt0 тяжелого бетона при непродолжительном действии нагрузок:
εbt0 = 0,0001.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
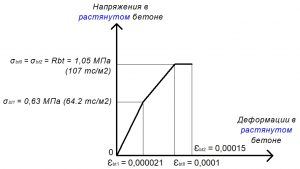
Рис. 18. Трехлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb1 = σb2 = 14,5 МПа.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения приведенного модуля деформации бетона Eb,red принимают:
Eb,red = Rb / εb1,red
Значения относительных деформаций εb1,red принимают при непродолжительном действии нагрузки:
εb1,red = 0,0015;
Eb,red = 14,5 / 0,0015 = 9666,7;
εb1 = Rb / Eb,red = 14,5 / 9666,7 = 0,0015.
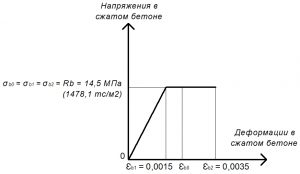
Рис. 19. Двухлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt1 = σbt2 = 1,05 МПа.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
Значения приведенного модуля деформации бетона Ebt,red принимают:
Ebt,red = Rbt / εbt1,red
Значения относительных деформаций εbt1,red принимают при непродолжительном действии нагрузок:
εbt1,red = 0,00008;
Ebt,red = 1,05 / 0,00008 = 13125;
εbt1 = Rbt / Ebt,red = 1,05 / 13125 = 0,00008.
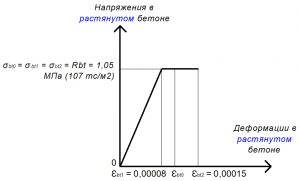
Рис. 20. Двухлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Двухлинейная диаграмма состояния (деформирования) арматуры при полной расчетной нагрузке

Рис. 21. Двухлинейная диаграмма состояния арматуры из СП 63.13330
Расчетное сопротивление растяжению арматуры Rs:
Rs = σs0 = σs2 = 430 МПа (для А500С).
Расчетное сопротивление сжатию арматуры Rs:
Rsс = σsс0 = σsс2 = 400 МПа (для А500С).
Значения модуля упругости арматуры принимают одинаковыми при растяжении и сжатии и равными, для арматуры А500С:
Es = 200000 МПа.
Значения относительных деформаций растянутой арматуры εs0 принимают равными:
для арматуры с физическим пределом текучести
εs0 = Rs / Es = 435 / 200000 = 0,002175.
Значения относительных деформаций сжатой арматуры εsс0 принимают равными:
для арматуры с физическим пределом текучести
εsс0 = Rsс / Es = 400 / 200000 = 0,002.
Значения относительной деформации εs2 принимают равными 0,025.
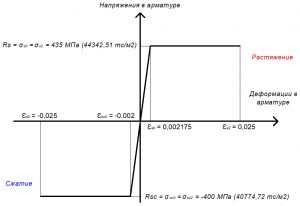
Рис. 22. Двухлинейная диаграмма состояния арматуры класса А500С при полной расчетной нагрузке
Ссылки по теме:
- Пример расчета нелинейного прогиба железобетонной балки по СП 63 в программе ЛИРА-САПР;
- Научно-методологические основы получения, описания, совершенствования и применения диаграмм деформирования бетона. Сравнительный анализ некоторых из известных по критерию энергозатрат. (Источник: «https://scadsoft.com/uploads/31«);
Источник
М.Н.ШЕСТЕРКИН, инж. (НИИЖБ), Свойства арматурной стали класса А500С, поступающей на стройплощадки Москвы
В настоящее время в России осуществляется переход на новую арматурную сталь, применяемую в обычном железобетоне единого класса — А500С. Она заменяет все классы арматурных сталей от А240 (А-I) до А600 (A-IV). На стройках Москвы применение этой стали регламентируется стандартом СТО АСЧМ 7-93, требования которого соответствуют требованиям евростандарта EN 10080 и международного стандарта ISO 6935, а также территориальными строительными нормами ТСН 102-00 /1, 21. Арматура данного класса может применяться в любых климатических зонах страны при температурах от +50 до -70°С б.ез ограничений во всех видах железобетонных конструкции и арматурных изделий.
Большинство металлургических заводов у нас в стране и странах СНГ уже выпускают арматуру класса А500С. Это Криворожский, Западно- Сибирский (ЗСМК) и Череповецкий меткомбинаты, а также Белорусский (БМЗ) и Молдавский метзаводы. Арматура этих заводов изготавливается способом термомеханического упрочнения (ТМУ) в потоке проката. Чусовским метзаводом (ЧМЗ), единственным в России, освоено производство горячекатаной арматурной стали класса А500С. В ближайшее время планируется освоение выпуска арматуры данного класса на всех металлургических заводах России.
В связи с началом широкого внедрения арматуры класса А500С в строительство, на протяжении ряда лет сотрудниками НИИЖБ это сталь производства Криворожского меткомбината (порядка 70-80%). Остальные заводы распределяются по объемам поставок в следующем образом: ЗСМК -15%, БМЗ -10%, ЧМЗ — 5% (данные — по строительству объекта ММДЦ «Москва-Сити»), Следует отметить, что в зависимости от поставщиков на отдельно взятых стройплощадках, процент применяемой арматурной стали класса А500С может колебаться в значительных пределах.

Требования стандарта к содержанию основных элементов и химический состав арматурной стали класса А500С поступающей на стройки Москвы приведены в таблице 1.
Анализ полученных данных показывает, что основные марки стали используемые металлургическими заводами — это Ст.ЗГпс и 20ГС. ЧМЗ выпускает арматуру класса А500С из стали марки 20ГСФ/3 /.
Несмотря на то, что на строительных объектах преобладает арматура класса А500С Криворожского МК вся арматурная сталь периодического профиля и других метзаводов подвергалась всестороннему исследованию ее механических свойств, прочности сварных соединений, а также геометрических размеров и погонной массы стержней. Результаты исследований геометрических размеров профиля приведены в таблице 2.
Геометрические размеры периодического профиля и массы 1 п. м. стержня полностью соответствуют осуществлялся контроль качества арматурной стали, поступающей на стройки Москвы для оценки соответствия ее свойств выше указанным стандарту и нормам. За период с 1999 по 2001 г. включительно, при осуществлении входного контроля качества арматурной стали было испытано на растяжение по методике ГОСТ 12004 более 550 образцов от 276 партий-плавок диаметром 10-36 мм. Дополнительно, в соответствии с требованиями стандарта СТО АСЧМ 3-93 были проведены испытания образцов арматурной стали на изгиб.
Подавляющее большинство арматуры класса А500С поступающей на строительные объекты, требованиям стандарта для арматуры класса А500С. Следует отметить тот факт, что погонная масса стержней мелких диаметров (10-12 мм) зачастую поступает на стройплощадки с плюсовым допуском, а более крупных (20-36 мм) с минусовым. Величина относительной площади смятия f, выступов является обобщенной характеристикой прочности сцепления арматурного стержня с бетоном. Нормируемая величина fr для арматуры диаметром 10-40 мм включительно, имеет значение 0,056. Данные исследований показали, что в зависимости от завода-изготовителя и диаметра арматуры, величина fr колеблется в пределах от 0,066 до 0,074.

Анализ полученных данных механических испытаний (см.табл.З) показал достаточно высокие средние значения предела текучести от. Его величина колеблется в пределах 569,3-611,0 Н/мм2. Среднее значение в генеральной совокупности по всем диаметрам составляет 585,2 Н/мм2, а нормативное значение с обеспеченностью более 95% (X-1.64S) — 517,4 Н/мм2. При этом, значение расчетного сопротивления Rs=450 Н/мм2 обеспечивается с величиной более 99,9%. Среднее значение временного сопротивления ав по всем испытанным диаметрам составляет 714,8 Н/мм2, а нормативное значение — 640,8 Н/мм2, что значительно превышает требуемую стандартом величину 600 Н/мм2.


Диаграмма растяжения арматуры класса А500С относительного удлинения при разрыве 65, в зависимости от диаметра арматуры, составляют 19,2- 21,9 %. При этом, нормативные значения лежат в пределах 16,8-19,0%, а в генеральной совокупности по всему исследованному сортаменту -17,1%.
Усредненная диаграмма растяжения испытанной арматурной стали класса А500С (см. рис.) характеризуется явно выраженной площадкой текучести и, в зависимости от диаметра арматуры, ее длина составляет 0,19-0,56% для ТМУ и 0,84- 2,02% для горячекатаной арматурной стали. Среднее значение относительного равномерного удлинения 5Р для ТМУ арматуры составляет 9,2%, а для горячекатаной 11,3%, при нормируемом значении — не менее 2%.
Все испытанные образцы на изгиб в холодном состоянии вокруг оправки, регламентированной СТО АСЧМ 7-93 на 180°, выдержали испытание.
Прочность сварных соединений стержней арматуры класса А500С, выполненных ванной сваркой на стальной скобе и внахлестку по ГОСТ 14098-91, в условиях стройплощадки показали снижение временного сопротивления для горячекатаной стали в ванных стыках до 5%, а в нахлесточных до 4%. Испытания нахлесточных соединений ТМУ стали класса А500С показали, что величина разупрочнения в зоне сварки не превышает 4,5%.
Оценивая результаты испытаний, можно отметить, что в обоих случаях величина временного сопротивления сварных соединений превышает нормируемую величину в первом случае на 8-16%, а во втором на 13-15%.
Проведенные исследования свойств арматуры класса А500С, поступившей на стройки Москвы за 1999-2001 г.,позволяет сделать вывод о том, что по своим прочностным показателям, по пластичности и свариваемости она не только отвечает требованиям Российских и международных стандартов, но в ряде случаев и превосходит их.
Бетон и железобетон, 2002 №1
Источник
