Диаграмма напряжения при деформации растяжения

Графическое изображение зависимости между напряжениями (или нагрузками) и деформациями материала (или перемещениями при деформировании) представляет собой диаграмму деформирования.
Испытательные машины имеют специальные приспособления, которые автоматически фиксируют диаграмму растяжения. На диаграмме по оси ординат откладываются действующие осевые нагрузки, а по оси абсцисс — абсолютные деформации.
На рис. 2.2 даны типичные диаграммы растяжения различных металлов. Диаграмма с постепенным переходом из упругой в пластическую область (рис. 2.2, а) свойственна большинству металлов в пластичном состоянии (легированные стали, медь, бронза).

Рис. 2.2. Диаграммы растяжения:
а — для большинства металлов в пластичном состоянии с постепенным переходом из упругой в пластическую область; б — для некоторых металлов в пластичном состоянии со скачкообразным переходом в пластическую область; в — для хрупких металлов
Пластичные материалы разрушаются при больших остаточных деформациях (больших остаточных удлинениях, измеряемых после разрыва).
Диаграмма со скачкообразным переходом в пластическую область в виде четко обозначенной «площадки» текучести (рис. 2.2, б) свойственна некоторым металлам. К таким металлам можно отнести мягкую углеродистую сталь, а также некоторые отожженные марганцовистые и алюминиевые бронзы.
Хрупкие материалы разрушаются при малых остаточных деформациях. К хрупким материалам можно отнести закаленную и неотпущенную сталь, серый чугун.
Характерные участки и точки диаграммы растяжения показаны на рис. 2.3. По оси абсцисс откладывают абсолютные удлинения А/ образца, а по оси ординат — значения растягивающей силы Р. Сначала получим на первом участке диаграммы 0—1 прямолинейную зависимость между силой и удлинением, что отражает закон Гука. При дальнейшем увеличении силы (за точкой 1) прямолинейная зависимость между Р и А/ нарушается. Точка 1 соответствует пределу пропорциональности, т. е. наибольшему напряжению, при котором еще соблюдается закон Гука. Если нагрузку, соответствующую точке 1, обозначить ,Pnu, а начальную площадь сечения образца Fq, то предел пропорциональности


Рис. 2.3. Характерные участки и точки диаграммы растяжения
Несколько выше точки 1 находится точка Г, соответствующая пределу упругости. Если нагрузку, соответствующую точке Г, обозначить через Руп, то предел упругости

По ГОСТу предел упругости задается и обозначается ag os — напряжение, при котором остаточное удлинение достигает 0,05 % длины участка образца, равного базе тензометра.
За точкой Г возникают уже заметные остаточные деформации. В точке 2 диаграммы частицы материала начинают переходить и область пластичности — наступает явление текучести образца.
На диаграмме растяжения получается горизонтальный участок 2—3 (площадка текучести), параллельный оси абсцисс. Для участка 2—3 характерен рост деформации без заметного увеличения нагрузки. Обозначим величину нагрузки, соответствующей площадке текучести 2—3, через Рт. Напряжение ат, отвечающее этой нагрузке, это то напряжение, при котором рост деформации происходит без заметного увеличения нагрузки, оно и является физическим пределом текучести.
Предел текучести (физический) — это механическая характеристика материалов: напряжение, отвечающее нижнему положению площадки текучести в диаграмме растяжения для материалов, имеющих эту площадку (см. рис. 2.3):

Предел текучести устанавливает границу между упругой и упруго-пластической зонами деформирования.
Даже небольшое увеличение напряжения (нагрузки) выше предела текучести вызывает значительные деформации.
Для материалов, не имеющих на диаграмме площадки текучести, принимают условный предел текучести: напряжение, при котором остаточная деформация образца достигает определенного значения, установленного техническими условиями (большего, чем это установлено для предела упругости).
Обычно допуском для величины остаточной деформации при растяжении принято остаточное удлинение 0,2 %. Эта величина называется условным пределом текучести:

где Pq 2 — нагрузка при условном пределе текучести.
При увеличении напряжений сверх предела текучести при растяжении в результате сильной деформации происходит упрочнение металла (изменение его структуры и свойств) и сопротивление деформации увеличивается, поэтому за участком текучести, т. е. за точкой 3, наблюдается подъем кривой растяжения (участок упрочнения). До точки 4 удлинение образца происходит равномерно. Наибольшее значение нагрузки, предшествовавшее разрушению образца, обозначим Рмакс. Точка 4 характеризует максимальное условное напряжение, возникающее в процессе испытания, называемое временным сопротивлением.
Временное сопротивление ав — условное напряжение, определяемое по отношению действующей силы к исходной площади поперечного сечения образца и отвечающее наибольшей нагрузке ^макс’ предшествовавшей разрушению образца:

В момент, соответствующий нагрузке Рмакс, появляется заметное местное сужение образца (шейка). Если до этого момента образец имел цилиндрическую форму, то теперь растяжение образца сосредоточивается в области шейки.
Участку 4—5 соответствует быстрое уменьшение сечения шейки, вследствие чего растягивающая сила уменьшается, хотя напряжение растет (площадь сечения в шейке ^врFq).
При дальнейшей деформации шейка сужается и образец разрывается по наименьшему сечению FK, где напряжения в действительности достигают наибольшей величины. Таким образом, нарастание пластической деформации при растяжении происходит поэтапно: равномерная пластическая деформация до точки 4 и местная пластическая деформация от точки 4 до точки 5 — момента разрушения.
Моменту разрыва соответствует точка 5, усилие разрыва обозначим Рк. Отношение разрывающего усилия к действительной площади сечения в месте разрыва называется истинным сопротивлением разрыву:

У пластичных металлов в является характеристикой сопротивления пластической деформации, а у хрупких — характеристикой сопротивления разрушению.
Для пластичных материалов, образующих при растяжении шейку, характеристикой сопротивления разрушению служит истинное сопротивление разрыву (при разрушении).
При определении пределов пропорциональности, упругости, текучести и временного сопротивления соответствующая им нагрузка Р относилась к начальной площади поперечного сечения образца, т. е. площади образца до испытания. При растяжении образца в области упругой деформации или близко от нее, т. е. при определении пределов пропорциональности и упругости, можно пренебречь небольшим изменением площади сечения образца.
Однако в области пластической деформации изменение сечения образца становится значительным. Поэтому теоретически возможно для определения временного сопротивления и предела текучести относить соответствующую нагрузку не к исходной площади образца, а к его действительной площади, которую он имеет в момент приложения соответствующей нагрузки.
Напряжения, определенные по отношению приложенной нагрузки к начальной площади образца, называются условными напряжениями, а определенные по отношению к действительной площади — истинными.
На рис. 2.4 дана диаграмма истинных напряжений. В диаграмме по оси абсцисс откладывается относительное удлинение с = Д///0, а по оси ординат — нормальное напряжение а = P/Fq, где /0 и Fq — первоначальные длина и площадь сечения образца. Диаграмма в координатах «напряжения — деформации» на участке 4—5 является условной, как было указано выше. При напряжении, соответ-

Рис. 2.4. Диаграмма истинных напряжений ствующем временному сопротивлению (точка 4), образуется шейка и площадь сечения резко уменьшается, поэтому истинное напряжение увеличивается и истинная диаграмма 4—5′ расположена выше условной диаграммы 4—5.
Следует отметить, что временное сопротивление не совпадает с сопротивлением разрыву и оказывается меньше последнего. Истинное сопротивление разрыву получается делением наибольшей нагрузки Рпч (точка 4′) на истинную уменьшенную площадь сечения FBp в момент начала появления шейки.
Таким образом, истинные напряжения с увеличением деформации непрерывно растут до момента разрушения образца.
Показателем пластической деформации является его абсолютное остаточное удлинение А/0Ст.п ПРИ разрыве (отрезок ОЛ[ на рис. 2.3), так как упругая деформация (отрезок A^2) исчезает после разрыва:

где /0 — начальная длина образца, /к — конечная длина образца (рис. 2.5).
Общее удлинение образца при растяжении слагается из равномерного и сосредоточенного удлинения (за счет образования шейки). Так как размеры испытуемых образцов могут быть различными, то характеристикой пластичности образца служит не его абсолютное, а относительное остаточное удлинение при разрыве 6 — отношение приращения расчетной длины образца после разрыва
 к первоначальной расчетной длине /0 в процентах:
к первоначальной расчетной длине /0 в процентах:

Чем больше 5, тем пластичнее металл.

Рис. 2.5. Образцы до растяжения (а) и после растяжения (б)
Другой характеристикой пластичности металла является относительное сужение сечения ц/ после разрыва (в процентах) — отношение разности начальной площади и минимальной площади поперечного сечения образца разрыва к начальной площади поперечного сечения образца.
Если Fq — начальная площадь образца, FK — минимальная площадь сечения в месте образования шейки (в месте разрыва), то относительное сужение (в процентах)

При оценке свойств образцов пластических материалов большое значение имеет их сопротивление пластической деформации. Оно показывает, какое напряжение можно допустить, не вызывая (или вызывая допускаемую величину) пластической деформации, т. е. изменения металла под действием внешних сил.
Свойства, характеризующие сопротивление пластической деформации, можно разделить на две группы: сопротивление металла малым пластическим деформациям и сопротивление металла значительным пластическим деформациям.
Величиной, характеризующей сопротивление малым пластическим деформациям, является предел упругости. Свойства сопротивления металла значительным пластическим деформациям проявляются при напряжениях выше условного предела текучести. Для пластических металлов временное сопротивление определяет сопротивление их значительным пластическим деформациям. Временное сопротивление является основной характеристикой хрупких материалов, разрушающихся при малых пластических деформациях.
В табл. 2.1 приведены механические характеристики некоторых материалов.
Источник
Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.
Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).
Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.
Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
На рис. 1 показана диаграмма для малоуглеродистой стали. Она построена в системе координат F-Δl, где:
F — продольная растягивающая сила, [Н];
Δl — абсолютное удлинение рабочей части образца, [мм]

Рис. 1 Диаграмма растяжения стального образца
Как видно из рисунка, диаграмма имеет четыре характерных участка:
I — участок пропорциональности;
II — участок текучести;
III — участок самоупрочнения;
IV — участок разрушения.
Построение диаграммы
Рассмотрим подробнее процесс построения диаграммы.
В самом начале испытания на растяжение, растягивающая сила F, а следовательно, и деформация Δl стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О).
На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня Δl растут пропорционально увеличивающейся нагрузке F.
После прохождения точки А диаграмма резко меняет свое направление и на участке II начинающемся в точке B линия какое-то время идет практически параллельно оси Δl, то есть деформации стержня увеличиваются при практически одном и том же значении нагрузки.
В этот момент в металле образца начинают происходить необратимые изменения. Перестраивается кристаллическая решетка металла. При этом наблюдается эффект его самоупрочнения.
После повышения прочности материала образца, диаграмма снова «идет вверх» (участок III) и в точке D растягивающее усилие достигает максимального значения. В этот момент в рабочей части испытуемого образца появляется локальное утоньшение (рис. 2), так называемая «шейка», вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).

Рис. 2 Стальной образец с «шейкой»
Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения образца, растягиваещее усилие необходимое для его растяжения уменьшается, и кривая диаграммы «идет вниз».
В точке E происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована «шейка»
Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:
W=0,8Fmax∙Δlmax
По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.
Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.
Предел пропорциональности >
Примеры решения задач >
Лабораторные работы >
Источник
Замерами диаметров образцов 3 и 4 после растяжения и разгрузки было установлено, что эти образцы находились в начальной стадии образования шейки. Поэтому две крайние правые точки этих кривых не относятся к стадии равномерной деформации. Это же подтверждается также поведением кривых о ] и при ер> 17%, первая из которых напоминает диаграмму истинных напряжений растяжения.
[c.41]
Для определения механических характеристик на практике используют условные диаграммы растяжения в координатах о — е. Построение диаграмм истинных напряжений значительно сложнее, и служат они главным образом целям теоретических исследований.
[c.100]
Конечная максимальная ордината в диаграмме истинных напряжений при растяжении называется сопротивлением разрушению и обозначается символом Ск.
[c.113]
Диаграмма напряжений при растяжении хрупких материалов имеет вид, изображенный на рис. 2.23. Так как при этом к моменту разрушения наблюдаются малые деформации и, в частности, вовсе не возникает шейки, диаграмма истинных напряжений очень незначительно отклоняется от условной.
[c.114]
Чтобы убедиться в этом, проанализируем диаграммы истинных напряжений а(е), полученные по результатам опытов на растяжение для одного и того же материала, но при различных температурах То и Гь Условия испытания установим таким образом, что заметной релаксации напряжений при растяжении не происходит. Не рассматривая особых случаев, отме ТИМ, что в большинстве подобных опытов графики зависимости а(е) выглядят именно так, как это показано на рис. 2.2,п. Если по этим диаграммам построить функции Да ), пользуясь выражением (1.35), то можно заметить (рис.2.2, б), что при повышении температуры до Г] изменяется вид распределения /х(а ), которое больше растянуто вдоль оси г, причем значения плотностей вероятностей уменьшились. В соответствии с этим снижается значение [А стр и уменьшается величина предела текучести металла Сг Т).
[c.57]
Следовательно, удельная работа разрушения — это работа, поглощенная единичным объемом, пропорциональная площади диаграммы, полученной при испытании на растяжение она может быть определена расчетом или планиметрированием. При разрушении пластичных, вязких материалов площадь диаграммы истинное напряжение — истинное удлинение практически совпадает с удельной работой разрушения, затраченной на создание трещины. До тех пор, пока трещина не возникнет, эта работа может быть отнесена только к единице объема, иначе она была бы произвольной. Удельная работа разрушения в определенных пределах не зависит от способа нагружения, т. е. одно и то же ее значение получается при растяжении, сжатии и малоцикловой усталости.
[c.38]
Характер диаграммы растяжения зависит от природы и состояния металла, а также от формы и размера образца. Рабочая диаграмма растяжения является условной ввиду непостоянства поперечного сечения образца. Для построения диаграммы истинных напряжений
[c.44]
Временное сопротивление для пластичных металлов по формуле (48) получается меньше истинного сопротивления разрыву 5к, так как у образца к концу растяжения фактическая площадь сечения меньше начальной площади Рд. Для установления связи между напряжением и деформацией в том сечении, где происходит разрыв образца, строят диаграммы истинных напряжений по оси ординат откладывают истинное напряжение 5 , получаемое делением нагрузки Рк на фактическую площадь сечения образца
[c.97]
Для установления соотношений между напряжениями и деформациями при различных видах напряженного состояния особое значение имеют диаграммы истинных напряжений при растяжении (диаграммы 5=5(е), где 5 — истинное нормальное напряжение и е — истинная деформация).
[c.24]
Для определения 5в необходимо знать а для этого приходится проводить в процессе растяжения непрерывное или хотя бы многократное измерение минимальных размеров сечения образца, как это обычно делается при построении диаграммы истинных напряжений. К тому же Ов и 5в функционально связаны между собой. Действительно, в любой момент испытания на стадии равномерного удлинения
[c.158]
Отсюда видно, что при сжатии, в противоположность растяжению, 5Ро- Диаграммы истинных напряжений при сжатии строят обычно в координатах 5—8 (рис. 83, кривая 1), хотя в качестве меры деформации бо лее строго было бы использовать истинное относительное сжатие
[c.181]
Характер диаграммы растяжения зависит от природы и состояния металла, а также от формы и размера образца. Рабочая диаграмма растяжения является условной ввиду непостоянства поперечного сечения образца. Для построения диаграммы истинных напряжений необходимо нагрузку в любой стадии деформации относить не к первоначальной площади поперечного сечения образца, а к фактической, все уменьшающейся при растяжении образца площади.
[c.39]
Условной диаграммой растяжения на практике пользуются для определения механических характеристик материала. Диаграммой истинных напряжений, учитывающей действительные поперечные сечения образца на всех этапах его испытания, пользуются в металловедении при определении характеристик пластичности материала.
[c.31]
В ряде случаев при вытяжке с утонением необходимо заранее хотя бы приближенно выяснить, какими механическими свойствами будет обладать полученная деталь. Это нетрудно сделать, если воспользоваться диаграммой истинных напряжений, у которой по оси абсцисс отложены истинные деформации с , а по оси ординат — истинные напряжения о (фиг. 210). Истинные напряжения — это напряжения, отнесенные не к начальной площади поперечного сечения, как это принято при определении предела прочности з и предела текучести о называемых условными напряжениями, а к текущей площади поперечного сечения, которое при растяжении уменьшается.
[c.331]
ПОСТРОЕНИЕ ДИАГРАММЫ ИСТИННЫХ НАПРЯЖЕНИЙ ПРИ РАСТЯЖЕНИИ ДЛЯ ТЕРМИЧЕСКИ ОБРАБОТАННОЙ УГЛЕРОДИСТОЙ СТАЛИ
[c.160]
Диаграмма истинных напряжений может быть построена двумя методами а) путем многократного измерения уменьшающегося диаметра образца в процессе растяжения
[c.162]
Диаграмма истинных напряжений. В процессе растяжения образца в результате поперечного сужения площадь его сечения уменьшается, следовательно, действительные напряжения будут большими, чем найденные по формуле (2.1), при Р — условно принятой величиной постоянной.
[c.27]
Но в связи с трудностью построения диаграммы истинных напряжений (трудность определения площади сечения образца в каждый отдельный момент действия нагрузки) пользуются условными диаграммами растяжения.
[c.102]
На рис. 18 показаны диаграмма истинных напряжений 5 — 1з для металла, образующего шейку при растяжении, и для сопоставления— диаграмма а — е. Из этих диаграмм видно, что с увеличением деформации истинные напряжения непрерывно растут до момента разрушения образца, и у пластичных материалов максимальная на-
[c.22]
Если считать материал несжимаемым п пренебрегать изменением его плотности при деформации, то зависимость между интенсивностями напряжений и деформаций в точности совпадает с диаграммой истинных напряжений при растяжении, поскольку прн простом растяжении а равно растягивающему напряжению, а 8,- — относительному удлинению.
[c.138]
В широком интервале деформации описываются с помощью диаграммы механического состояния в сочетании с обобщенной диаграммой деформирования, представленными на рис. 1.4 (по Я. Б. Фридману). На диаграмме механического состояния по оси абсцисс наносят рассчитанные на основе гипотезы наибольших удлинений истинные напряжения растяжения Snp для данного напряженного состояния, по оси ординат — наибольшие истинные касательные напряжения imax для того же напряженного состояния. Одно из этих напряжений (действующих по своим площадкам) может вызвать разрушение в результате отрыва, если 5пр=5к, или среза, если tjanx=it. На диаграмме рис. 1,4,о нанесены соответ-
[c.11]
| Фиг. 15. Напряжённое состояние деформируемого металла при осадке (Корнеев) а —вид напряжённого состояния при осадке в местах действия дополнительных рас-тигивающих напряжений 5-диаграммы истинных напряжений при растяжении. | 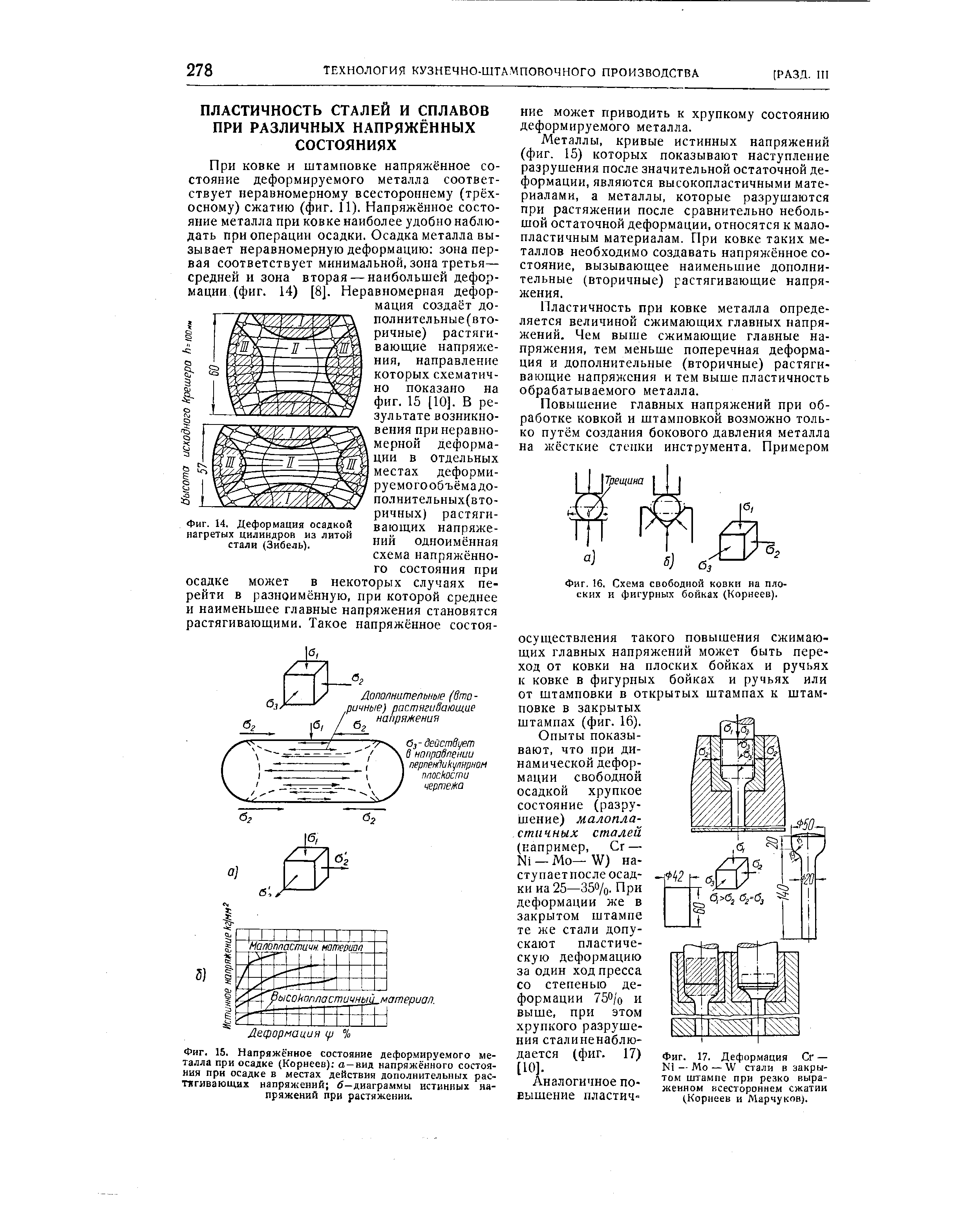 |
В качестве примера рассмотрим расчет свойств стали 50ХГФА. Для обеспечения работы математической модели сопротивления деформации были проведены испытания образцов этой стали на растяжение при температурах 20, 800 и 900 на разрывной машине Р-5. По испытаниям пяти образцов для каждой из температур были получены и усреднены диаграммы истинных напряжений. Статистическая обработка результатов опытов показала, что при вероятности 0,95 доверительный интервал значений напряжений не превышал 5 % от средних измеренных-величин.
[c.189]
Индикаторная диаграмма и диаграмма условных напряжений при растяжении и их характерные точки. Индикаторная диаграмма (рис. 56) отображает зависимость силы растяжения Р от абсолютного удлинения 1 = 1 — 1 , где I — текущая длина рабочей части образца, на которой определяется удлинение, Чтобы устранить масштабный фактор, строят диаграмму условных напряжений — зависимость условного напряжения Оуел = Р Р , где Fq == ndyA — начальная площадь поперечного сечения образца, от относительного удлинения е = Строят также диаграмму истинных напряжений (кривую упрочнения первого рода) зависимость истинного напряжения ст ст = — Р/Р от я, где F — текущая площадь поперечного сечения образца. Истинное напряжение называют еще сопротивлением металла деформации.
[c.155]
S — сопротивление разрушению (колеч-ная ордината диаграммы истинных напряжений прн растяжении). Термином С, с. пользуются также для оценки условного напряжения, характеризующего прочность болтов, заклепок и др. элементов, в условиях двойного или одинарного среза (см. Испытание на срез). Это условное С. с. обозначается символом т .р.
[c.181]
Расчёт плоских спиральных заневоленных пружин [4], [17]. При расчёте следует руководствоваться диаграммой истинных напряжений пружинной ленты при растяжении (фиг. 39) предполагается, что материал имеет при растяжении и сжатии одинаковые механические характеристики. В сечении ленты на радиусе р(р1относительное удлинение в крайнем волокне ленты
[c.896]
На диаграмме истинных напряжений почти всегда бывает отмечена равномерная деформация Травн, соответствующая началу появления шейки на образце при испытании на растяжение. Истинное
[c.331]
Расчет плоских спиральных заневоленных пружин [4], [17]. При расчете следует руководствоваться диаграммой истинных напряжений пружинной ленты при растяжении (фиг. 42) предполагается, что материал имеет при растяжении и сжатии одинаковые механические характеристики. В сечении ленты
[c.649]
Из всех методов определения механических свойств металла наилучшие результаты дает испытание на растяжение, которое позволяет определить такие характеристики сопротивления деформации, как предел текучести, предел прочности, истинное сопротивление разрыву (а а , а ст) и показатели пластичности — относительное удлинение и относительное поперечное сужение (5 и 4 )- Зависимость между напряжением и деформацией наиболее правильно выражается диаграммой истинных напряжений в координатах истинные напряжения — относительное поперечное сужение (иист — Ф)-
[c.429]
Свойства сталей после закалки и отпуска непосредственно свя заны с процессами, проходящими при отпуске. При низкой температуре отпуска (до ЗООР) происходит распад мартенсита с образованием цементитного карбида, причем выделяющийся карбид как в углеродистой, так и в легированной стали имеет высокую степень дисперсности, мало меняющуюся с температурой отпуска [45]. Леги рующие элементы находятся практически целиком в твердом раство ре. Твердость стали при низком отпуске зависит от содержания углерода в а-растворе и до температуры 200° практически не зависит от количества выделившихся карбидных частиц [46]. При оди наковом содержании углерода в мартенсите легирующие элементы не влияют на твердость низкоотпущенной стали. Основная роль легирующих элементов при низком отпуске, как и для мартенсита, сводится к повышению пластичности. В качестве примера на фиг. 30 приведены диаграммы истинных напряжений при растяжении 44
[c.44]
Справочник машиностроителя Том 2
(1952) — [
c.5
]
Источник
