Диаграмма бетона при сжатии и растяжении
1. Проектные классы и марки бетона.
Являются показателями качества б.
Класс по прочности на осевое сжатие– В 3,5…70 – временное сопротивление
сжатию в МПа кубов с размером ребра 15
см, испытанных через 28сут хранения приtºС=20±2оС по ГОСТ и
с обеспеченностью 0,95. Основная хар-ка.Класс по прочности на осевое растяжениеBt0,8…3,2 – временное сопротивление
растяжению в МПа с учетом статистической
изменчивости. Указывается, когда эта
хар-ка имеет главенствующее значение
и контролируется на производстве.Марка
по морозостойкостиF25…500 – количество циклов поперечного
замораживания и оттаивания в насыщенном
водой состоянии, которое выдерживает
образец до разрушения. Назначают для
конструкций, подвергающихся попеременному
замораживанию и оттаиванию (открытые
конструкции, ограждающие конструкции
и т. п.).Марка по водонепроницаемости
W2…12 – максимальное
давление воды, при котором еще не
наблюдается ее просачивания через
образец. Число – количество выдерживаемых
атмосфер или предельное давление воды
в кг/см2. Назначают для конструкций,
к которым предъявляют требования
ограниченной проницаемости (резервуары
и т.п.).Марка по среднейплотностиD800…2000 – указывается
в кг/м3. Назначают для конструкций,
к которым предъявляют кроме требований
прочности требования теплоизоляции, и
контролируют на производстве.Марка
по самонапряжению Sp.
Проектные классы и марки б. получают
соответствующим подбором состава
бетонной смеси с последующим испытанием
контрольных образцов.
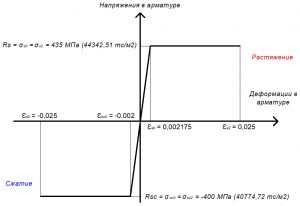
2. Полная диаграмма сжатия-растяжения бетона. Ветви диаграммы, координаты вершины. Определение модуля упругости бетона и секущего модуля деформаций.
Н ачальный
ачальный
модуль упругостипри сжатииEbсоответствует лишь упругим деформациям,
возникающим при мгновенном загружении:Eb=tgφ0(дается в СНиП).Модуль полных деформацийпри сжатииEb’
соответствует полным деформациям и
является величиной переменной:Eb’=tgφ.
Для расчета пользуютсясредним модулем
или модулем упругопластичности:Eb’=tgφ1(заменяет предыдущий).Eb’=Eb*υe,
где υe-коэффициент
упругости, υe=εe/εb,
где εe-упругие
деформации, εb-полные
деформации.
3. Классификация арматурной стали. Диаграммы растяжения арматурных сталей нормальной и высокой прочности. Определение прочностных характеристик и модуля упругости.
По форме | гибкая | жесткая | ||||
По применению | напрягаемая | ненапрягаемая | ||||
По форме | гладкая | периодического | ||||
По технологии | горячекатаная | холоднотянутая | ||||
AI-гладкая AII-непрерывная периодичность AIII-сходящаяся периодичность мягкие стали AIV- сходящаяся периодичность AV- сходящаяся периодичность AVI- сходящаяся периодичность твердые | AIIв AIIIв упрочненная | AтIII AтIV AтV AтVI упрочненная | BpI | BII-гладкая BpII-рифленая | K7 K19 канаты | |
С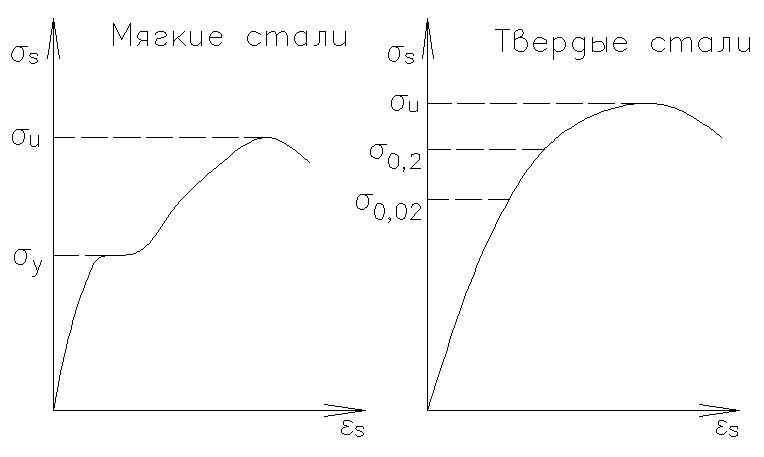 тали
тали
бываютобычные, повышенной прочности,
высокопрочные. Первый вид относится
кмягким сталям, второй и третий –
ктвердым. Характеристики прочности
и деформаций арматурных сталей
устанавливают по диаграмме σs-εs,
получаемой при испытании образцов на
растяжение.Мягкая стальимеет на
диаграмме площадку текучести, обладает
значительным удлинением после разрыва.
Напряжение, при котором деформации
развиваются без заметного увеличения
нагрузки, называетсяфизическим
пределом текучести арматурной стали
σy, напряжение в
начале образования шейки, предшествующее
разрыву, носит названиевременного
сопротивления арматурной стали σu.
Твердые сталипереходят в пластическую
стадию постепенно, что характеризуется
отсутствием ярко выраженной площадки
текучести на кривой. Для этих сталей
устанавливаютусловный предел текучести
– напряжение σ0,2, при котором
остаточные деформации составляют 0,2%,
а такжеусловный предел упругости –
напряжение σ0,02, при котором
остаточные деформации равны 0,02%.
Rsn=σy(мягкие
стали), =σ0,2(твердые стали)-стержни.
σ0,2=0,8σu-проволока
ВрI. Модуль упругостиEs=tgугла наклона касательной к эпюре.
Соседние файлы в папке Шпоры к госам_Железобетон
- #
- #
- #
- #
- #
- #
- #
14.05.2015212.4 Кб16рисунки жб.dwg
Источник
Для примера построения диаграмм взят наиболее часто используемый класс бетона (В25) и арматуры (А500С).
Для расчетов по второму предельному состоянию.
При нормативной длительной нагрузке (для определения прогибов ж/б плит)
Трехлинейная диаграмма
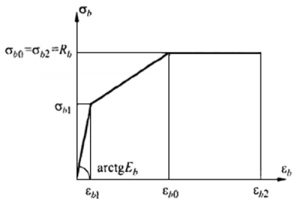
Рис. 1. Трехлинейная диаграмма состояния сжатого бетона из СП 63.13330
СП 63.13330.2012, п. 6.1.25: «При расчете деформаций железобетонных элементов по нелинейной деформационной модели при отсутствии трещин для оценки напряженно-деформированного состояния в сжатом и растянутом бетоне используют трехлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки. При наличии трещин для оценки напряженно-деформированного состояния сжатого бетона помимо указанной выше диаграммы используют, как наиболее простую, двухлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки«.
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb2 = Rb,n = 18,5 МПа.
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
При продолжительном действии нагрузки модуль деформации бетона определяют по формуле:
Eb,t = Eb / 1 + φb,cr = 30000 / 1 + 2,5 = 8571,43 МПа;
Коэффициент φb,cr при нормальной влажности (40-75%) равен 2,5.
При трехлинейной диаграмме значения напряжений σb1 определяют по формуле:
σb1 = 0,6 х Rb,n = 11,1 МПа;
а значения относительных деформаций εb1 принимают:
εb1 = σb1 / Eb,t = 11,1 / 8571,43 = 0,001295.
Значения относительных деформаций εb2 для тяжелого бетона при продолжительном действии нагрузок принимают по таблице 6.10:
εb2 = 0,0048.
Значения предельных относительных деформаций εb0 тяжелого бетона при продолжительном действии нагрузок и нормальной влажности (40-75%) принимают по таблице 6.10:
εb0 = 0,0034.
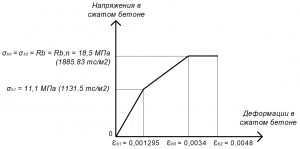
Рис. 2. Трехлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt2 = Rbt,n = 1,55 МПа.
При трехлинейной диаграмме значения напряжений σbt1 определяют по формуле:
σbt1 = 0,6 х Rbt,n = 0,93 МПа;
При продолжительном действии нагрузки модуль деформации бетона определяют по формуле:
Eb,t = Eb / 1 + φb,cr = 30000 / 1 + 2,5 = 8571,43 МПа;
Значения относительных деформаций εbt1 принимают:
εbt1 = σbt1 / Eb,t = 0,93 / 8571,43 = 0,0001085.
Значения предельных относительных деформаций εbt0 тяжелого бетона при продолжительном действии нагрузок и нормальной влажности (40-75%) принимают по таблице 6.10:
εbt0 = 0,00024.
Значения относительных деформаций εbt2 для тяжелого бетона при продолжительном действии нагрузок принимают по таблице 6.10:
εbt2 = 0,00031.
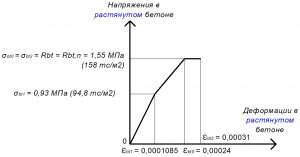
Рис. 3. Трехлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Двухлинейная диаграмма
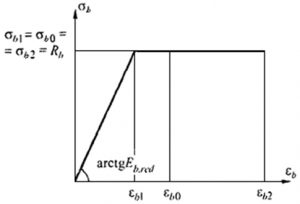
Рис. 4. Двухлинейная диаграмма состояния сжатого бетона из СП 63.13330
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb1 = σb2 = Rb,n = 18,5 МПа.
Значения относительных деформаций εb2 для тяжелого бетона при продолжительном действии нагрузок:
εb2 = 0,0048.
Значения приведенного модуля деформации бетона Eb,red принимают:
Eb,red = Rb,n / εb1,red
Значения относительных деформаций εb1,red принимают по таблице 6.10:
при нормальной влажности (40-75%) εb1,red = 0,0028;
Eb,red = 18,5 / 0,0028 = 6607,14;
εb1 = Rb,n / Eb,red = 18,5 / 6607,14 = 0,0028.
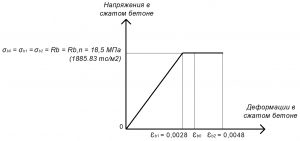
Рис. 5. Двухлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt1 = σbt2 = Rbt,n = 1,55 МПа.
Значения относительных деформаций εbt2 для тяжелого бетона при продолжительном действии нагрузок принимают по таблице 6.10:
εbt2 = 0,00031.
Значения приведенного модуля деформации бетона Ebt,red принимают:
Ebt,red = Rbt,n / εbt1,red
Значения относительных деформаций εbt1,red принимают по таблице 6.10:
при нормальной влажности (40-75%) εbt1,red = 0,00022;
Ebt,red = 1,55 / 0,00022 = 7045,45;
εbt1 = Rbt,n / Ebt,red = 1,55 / 7045,45 = 0,00022.
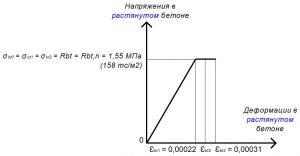
Рис. 6. Двухлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при нормативной длительной нагрузке и высоте бетонирования не более 1,5 м
Данные диаграммы построены для бетона при продолжительном действии нагрузок и могут использоваться при расчете прогибов. Для расчета ширины раскрытия трещин нужно строить диаграммы при непродолжительном действии нагрузок, см. п. 6.1.26 СП 63.13330: «При расчете раскрытия нормальных трещин по нелинейной деформационной модели для оценки напряженно-деформированного состояния в сжатом бетоне используют диаграммы состояния, приведенные в 6.1.20 и 6.1.21, с учетом непродолжительного действия нагрузки. При этом в качестве наиболее простой используют двухлинейную диаграмму состояния бетона».
Двухлинейная диаграмма состояния (деформирования) арматуры при нормативной длительной нагрузке
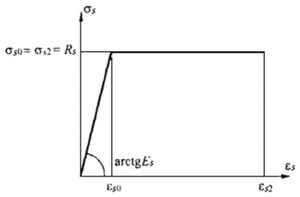
Рис. 7. Двухлинейная диаграмма состояния арматуры из СП 63.13330
Расчетное сопротивление растяжению арматуры Rs:
Rs = σs0 = σs2 = Rs,n = 500 МПа (для А500С).
Значения модуля упругости арматуры принимают одинаковыми при растяжении и сжатии и равными, для арматуры А500С:
Es = 200000 МПа.
Значения относительных деформаций арматуры εs0 принимают равными:
для арматуры с физическим пределом текучести
εs0 = Rs,n / Es = 500 / 200000 = 0,0025.
Значения относительной деформации εs2 принимают равными 0,025.
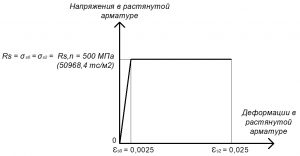
Рис. 8. Двухлинейная диаграмма состояния растянутой (или сжатой) арматуры класса А500С при длительной нормативной нагрузке
При расчете железобетонных элементов по нелинейной деформационной модели в качестве расчетной диаграммы состояния (деформирования) арматуры, устанавливающей связь между напряжениями σs и относительными деформациями εs арматуры, для арматуры с физическим пределом текучести классов А240-А500, В500 принимают двухлинейную диаграмму. Диаграммы состояния арматуры при растяжении и сжатии принимают одинаковыми, с учетом нормируемых расчетных сопротивлений арматуры растяжению и сжатию.
Для расчетов по второму предельному состоянию.
При полной нормативной нагрузке (для проверки ширины раскрытия трещин)
Трехлинейная диаграмма

Рис. 9. Трехлинейная диаграмма состояния сжатого бетона из СП 63.13330
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb2 = Rb,n = 18,5 МПа.
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
При трехлинейной диаграмме значения напряжений σb1 определяют по формуле:
σb1 = 0,6 х Rb = 11,1 МПа;
а значения относительных деформаций εb1 принимают:
εb1 = σb1 / Eb = 11,1 / 30000 = 0,00037.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения предельных относительных деформаций εb0 тяжелого бетона при непродолжительном действии нагрузок:
εb0 = 0,002.
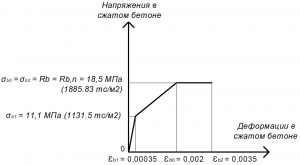
Рис. 10. Трехлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt2 = 1,55 МПа.
При трехлинейной диаграмме значения напряжений σbt1 определяют по формуле:
σbt1 = 0,6 х Rbt = 0,93 МПа;
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
Значения относительных деформаций εbt1 принимают:
εbt1 = σbt1 / Eb = 0,93 / 30000 = 0,000031.
Значения предельных относительных деформаций εbt0 тяжелого бетона при непродолжительном действии нагрузок:
εbt0 = 0,0001.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
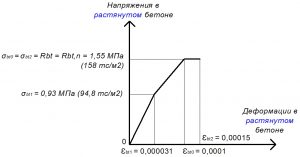
Рис. 11. Трехлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb1 = σb2 = 18,5 МПа.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения приведенного модуля деформации бетона Eb,red принимают:
Eb,red = Rb / εb1,red
Значения относительных деформаций εb1,red принимают при непродолжительном действии нагрузки:
εb1,red = 0,0015;
Eb,red = 18,5 / 0,0015 = 12333,3;
εb1 = Rb / Eb,red = 18,5 / 12333,3 = 0,0015.
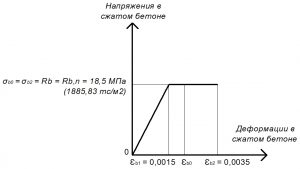
Рис. 12. Двухлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt1 = σbt2 = 1,55 МПа.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
Значения приведенного модуля деформации бетона Ebt,red принимают:
Ebt,red = Rbt / εbt1,red
Значения относительных деформаций εbt1,red принимают при непродолжительном действии нагрузок:
εbt1,red = 0,00008;
Ebt,red = 1,55 / 0,00008 = 19375;
εbt1 = Rbt / Ebt,red = 1,55 / 19375 = 0,00008.
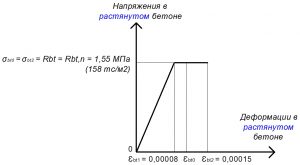
Рис. 13. Двухлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной нормативной нагрузке и высоте бетонирования не более 1,5 м
Двухлинейная диаграмма состояния (деформирования) арматуры при полной нормативной нагрузке

Рис. 14. Двухлинейная диаграмма состояния арматуры из СП 63.13330
Расчетное сопротивление растяжению арматуры Rs:
Rs = σs0 = σs2 = 500 МПа (для А500С).
Расчетное сопротивление сжатию арматуры Rs:
Rsс = σsс0 = σsс2 = 500 МПа (для А500С).
Значения модуля упругости арматуры принимают одинаковыми при растяжении и сжатии и равными, для арматуры А500С:
Es = 200000 МПа.
Значения относительных деформаций растянутой арматуры εs0 принимают равными:
для арматуры с физическим пределом текучести
εs0 = Rs / Es = 500 / 200000 = 0,0025.
Значения относительных деформаций сжатой арматуры εsс0 принимают равными:
для арматуры с физическим пределом текучести
εsс0 = Rsс / Es = 500 / 200000 = 0,0025.
Значения относительной деформации εs2 принимают равными 0,025.
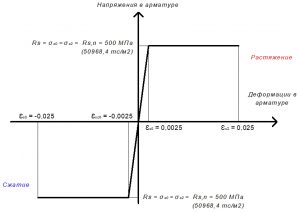
Рис. 15. Двухлинейная диаграмма состояния арматуры класса А500С при полной нормативной нагрузке
Для расчетов по первому предельному состоянию.
При полной расчетной нагрузке (для проверки прочности)
Трехлинейная диаграмма

Рис. 16. Трехлинейная диаграмма состояния сжатого бетона из СП 63.13330
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb2 = 14,5 МПа.
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
При трехлинейной диаграмме значения напряжений σb1 определяют по формуле:
σb1 = 0,6 х Rb = 8,7 МПа;
а значения относительных деформаций εb1 принимают:
εb1 = σb1 / Eb = 8,7 / 30000 = 0,00029.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения предельных относительных деформаций εb0 тяжелого бетона при непродолжительном действии нагрузок:
εb0 = 0,002.
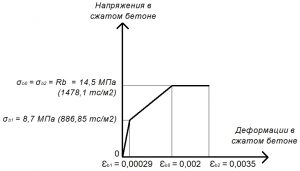
Рис. 17. Трехлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt2 = 1,05 МПа.
При трехлинейной диаграмме значения напряжений σbt1 определяют по формуле:
σbt1 = 0,6 х Rbt = 0,63 МПа;
Начальный модуль упругости бетона при сжатии и растяжении:
Eb = 30000 МПа.
Значения относительных деформаций εbt1 принимают:
εbt1 = σbt1 / Eb = 0,63 / 30000 = 0,000021.
Значения предельных относительных деформаций εbt0 тяжелого бетона при непродолжительном действии нагрузок:
εbt0 = 0,0001.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
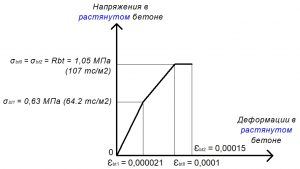
Рис. 18. Трехлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому сжатию:
Rb = σb0 = σb1 = σb2 = 14,5 МПа.
Значения относительных деформаций εb2 для тяжелого бетона при непродолжительном действии нагрузок принимают, для бетонов класса по прочности на сжатие В60 и ниже:
εb2 = 0,0035.
Значения приведенного модуля деформации бетона Eb,red принимают:
Eb,red = Rb / εb1,red
Значения относительных деформаций εb1,red принимают при непродолжительном действии нагрузки:
εb1,red = 0,0015;
Eb,red = 14,5 / 0,0015 = 9666,7;
εb1 = Rb / Eb,red = 14,5 / 9666,7 = 0,0015.
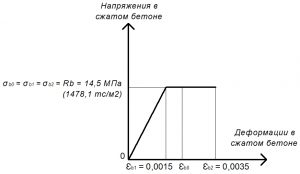
Рис. 19. Двухлинейная диаграмма состояния сжатого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Расчетные значения сопротивления бетона осевому растяжению:
Rbt = σbt0 = σbt1 = σbt2 = 1,05 МПа.
Значения относительных деформаций εbt2 для тяжелого бетона при непродолжительном действии нагрузок:
εbt2 = 0,00015.
Значения приведенного модуля деформации бетона Ebt,red принимают:
Ebt,red = Rbt / εbt1,red
Значения относительных деформаций εbt1,red принимают при непродолжительном действии нагрузок:
εbt1,red = 0,00008;
Ebt,red = 1,05 / 0,00008 = 13125;
εbt1 = Rbt / Ebt,red = 1,05 / 13125 = 0,00008.
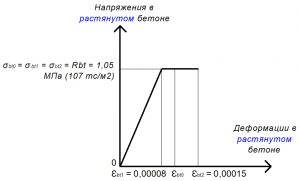
Рис. 20. Двухлинейная диаграмма состояния растянутого тяжелого бетона класса В25 по СП 63.13330 при полной расчетной нагрузке и высоте бетонирования не более 1,5 м
Двухлинейная диаграмма состояния (деформирования) арматуры при полной расчетной нагрузке

Рис. 21. Двухлинейная диаграмма состояния арматуры из СП 63.13330
Расчетное сопротивление растяжению арматуры Rs:
Rs = σs0 = σs2 = 430 МПа (для А500С).
Расчетное сопротивление сжатию арматуры Rs:
Rsс = σsс0 = σsс2 = 400 МПа (для А500С).
Значения модуля упругости арматуры принимают одинаковыми при растяжении и сжатии и равными, для арматуры А500С:
Es = 200000 МПа.
Значения относительных деформаций растянутой арматуры εs0 принимают равными:
для арматуры с физическим пределом текучести
εs0 = Rs / Es = 435 / 200000 = 0,002175.
Значения относительных деформаций сжатой арматуры εsс0 принимают равными:
для арматуры с физическим пределом текучести
εsс0 = Rsс / Es = 400 / 200000 = 0,002.
Значения относительной деформации εs2 принимают равными 0,025.

Рис. 22. Двухлинейная диаграмма состояния арматуры класса А500С при полной расчетной нагрузке
Ссылки по теме:
- Пример расчета нелинейного прогиба железобетонной балки по СП 63 в программе ЛИРА-САПР;
- Научно-методологические основы получения, описания, совершенствования и применения диаграмм деформирования бетона. Сравнительный анализ некоторых из известных по критерию энергозатрат. (Источник: «https://scadsoft.com/uploads/31«);
Источник
Реализация физически нелинейного расчета
Физически нелинейный расчет выполняется с использованием шагового процессора который позволяет получить напряженно-деформированное состояние с учетом нелинейных эффектов как для мономатериальных, так и для биматериальных конструкций.
Матрица жесткости линеаризованной физически нелинейной системы формируется на основании переменных интегральных жесткостей, вычисляемых в точках интегрирования конечного элемента при решении упругой задачи на конкретном шаге. Схема численного интегрирования по области конечного элемента и набор используемых жесткостей определяются типом конечного элемента. Для того чтобы получить соответствующий набор интегральных жесткостей, сечение конечного элемента в точках интегрирования дробится на ряд элементарных подобластей. В центрах этих подобластей определяются новые значения физико-механических характеристик материала в соответствии с заданной диаграммой деформирования. На каждом шаге решается линеаризованная задача с формированием векторов перемещений, усилий и новых интегральных жесткостей по касательному модулю для последующего шага. Количество шагов и коэффициенты к нагрузке задаются пользователем. Геометрическая интерпретация шагового метода для случая одноосного растяжения (сжатия) представлена на рисунке ниже
Подробно о методике расчета можно узнать в книге
И почитать статью в Базе знаний от разработчика: https://help.liraland.ru/984/3426/
Описание диаграмм деформирования
При выполнении физ. нелинейного расчета необходимо задать диаграммы деформирования (работы) материалов.
Диаграммы деформирования бетона могут быть приняты из существующей библиотеки (21, 25, 31, 35 законы деформирования) или заданы вручную (14, 15 законы). Для арматуры – 11 и 14 (задаются вручную).
Данные для построения диаграмм, создаваемых пользователем, можно принять из существующих норм на проектирование ж/б конструкций. В этом случае диаграмма описывается 14 кусочно-линейным законом
Диаграммы состояния сжатого бетона
а — трехлинейная диаграмма состояния сжатого бетона; б — двухлинейная диаграмма
Диаграмма состояния растянутой арматуры
При описании диаграммы 14 законом нельзя моделировать горизонтальные и ниспадающие участки. Таким образом, при построении диаграммы в соответствии с СП 52-2003/СП 63, горизонтальный участок следует моделировать небольшим уклоном площадки пластических деформаций. Следует отметить, что нормативные диаграммы деформирования не учитывают ниспадающую ветвь деформирования бетона (стадию разупрочнения).
Рекомендуем расчет выполнять с использованием стандартных диаграмм работы бетона –25 и 35 законы (в зависимости от того какие нужны характеристики). Для задания произвольных характеристик бетона можно воспользоваться 15 законом деформирования
При описании 15, 25 и 35 законов деформирования бетона обязательно следует задать предельные относительные деформации в соответствии с действующими нормами в зависимости от продолжительности действия нагрузки.
Для 11 закона деформирования стали значение предельной деформации при растяжении — 0.025.
Моделирование работы бетона в трещине
При достижении в элементарном слое поперечного сечения элемента напряжения равного Rbt должна возникнуть и раскрыться трещина. На данный момент шаговый процессор для пластинчатых элементов не умеет учитывать данную особенность. Получается, что элементарный слой продолжает пластически деформироваться с модулем упругости Е=1 и «держит» напряжения Rbt.
Это можно исправить следующим образом: ввести новую отсечку на диаграмме, так что при εb→0, Rbt→0 (законы 25, 35) или ввести Rbt→0. Таким образом, можно растянутый бетон полностью выключить из работы.
Так, бетон растянутой зоны исключается из работы при относительных деформациях соответствующих σb=Rbt
Если задать малую величину предельной деформации на растяжение ε, то можно «выключить» растянутый бетон из работы вовсе
Учет ползучести
Ползучесть можно описать степенным законом в соответствии с Еврокодом EN 1992-1-1 или можно задать произвольный кусочно-линейный закон (44)
Для учета ползучести бетона при физически нелинейном расчете следует установить флажок «Учитывать ползучесть бетона». После этого появляется третья закладка для задания законов ползучести бетона (в соответствии с EN 1992-1-1)
Источник
