Деформация растяжение и картинки

В машиностроении, строительстве и архитектуре при расчетах прочности и жесткости материалов используется математический аппарат технической механики. Деформация растяжения – одно из ключевых понятий, характеризующее механические процессы, происходящие в материалах при приложении к ним внешних воздействий. Для наглядности изучаются изменения, происходящие в брусе с постоянным сечением, характерные для упругой деформации при приложении внешних усилий.
Закон Гука (английский физик Р. Гук, 1653-1703) для упругой деформации растяжения/сжатия гласит, что нормальное напряжение находится в линейной зависимости (прямо пропорционально) к относительному удлинению/укорочению. Математический аппарат технической механики описывает эту формулу следующим образом:
Коэффициент пропорциональности E (модуль упругости, модуль Юнга) – величина определяющая жесткость материала, единица измерения – паскаль (ПА).
Его значения были установлены эмпирическим путем для большинства конструкционных материалов, необходимую информацию можно почерпнуть в справочниках по машиностроению. Относительная деформация является отношением изменения длины бруса к его изначальным размерам, это безразмерная величина, которая иногда отражается в процентном соотношении.
При растяжении или сжатии у бруса меняется не только длина, но происходят поперечные деформации: при сжатии образуется утолщение, при растяжении толщина сечения становится меньше. Величины этих изменений находятся в линейной зависимости друг от друга, причем установлено, что коэффициент пропорциональности Пуассона (фр. ученый С. Пуассон, 1781-1840) остается всегда неизменным для исследуемого материала.
Внутренние усилия при растяжении и сжатии
При приложении к брусу с постоянным сечением внешних воздействий, действие которых в любом поперечном разрезе направлено параллельно его центральной оси и перпендикулярно сечению, с ним происходит следующий вид деформации: растяжение или сжатие. На основе гипотезы о принципе независимости внешнего воздействия для каждого из поперечных разрезов можно рассчитать внутреннее усилие как векторную сумму всех приложенных внешних воздействий. Растягивающие нагрузки в сопромате принято считать положительными, а сжимающие отрицательными.
Рассмотрев произвольный разрез бруса или стержня, можно сказать что внутренние напряжения равны векторной сумме всех внешних сил, сгруппированных по одной из его сторон. Это верно только с учетом принципа Сен-Венана (фр. инженер А. Сен-Венан, 1797-1886) о смягчении граничных условий, т.к. распределение внутренних усилий по поверхности разреза носит сложный характер с нелинейными зависимостями, но в данном случае значением погрешности можно пренебречь как несущественным.
Применяя гипотезу Бернулли (швейцарский математик, И. Бернулли, 1667-1748) о плоских сечениях, для более наглядного представления процессов распределения сил и напряжений по центральной оси бруса можно построить эпюры. Визуальное представление более информативно и в некоторых случаях позволяет получить необходимые величины без сложных расчетов. Графическое представление отражает наиболее нагруженные участки стержня, инженер может сразу определить проблемные места и ограничиться расчетами только для критических точек.
Все вышесказанное может быть применимо при квазистатической (система может быть описана статически) нагрузке стержня с постоянным диаметром. Потенциальная энергия системы на примере растяжения стержня определяется по формуле:
U=W=FΔl/2=N²l/(2EA)
Потенциальная энергия растяжения U концентрируется в образце и может быть приравнена к выполнению работы W (незначительное выделение тепловой энергии можно отнести к погрешности), которая была произведена силой F для увеличения длины стержня на значение абсолютного удлинения. Преобразуя формулу, получаем, что вычислить значение величины потенциальной энергии растяжения можно, рассчитав отношение квадрата продольной силы N помноженной на длину стержня l и удвоенного произведения модуля Юнга E материала на величину сечения A.
Как видно из формулы, энергия растяжения всегда носит положительное значение, для нее невозможно применить гипотезу о независимости действия сил, т.к. это не векторная величина. Единица измерения – джоуль (Дж). В нижней части формулы стоит произведение EA – это так называемая жесткость сечения, при неизменном модуле Юнга она растет только за счет увеличения площади. Величина отношения жесткости к длине бруса рассматривается как жесткость бруса целиком.
Напряжения при растяжении сжатии
Используя гипотезу Бернулли для продольной упругой деформации стержня, можно определить продольную силу N как равнодействующую всех рассредоточенных по сечению внутренних усилий. Гипотеза Бернулли совместно с гипотезой о ненадавливании волокон позволяет сказать, что σ в произвольной точке разреза будут постоянны, т.к. реакция продольных волокон одинакова на всем поперечном разрезе. Для определения величины нормального напряжения σ используется следующая формула:
Напряжение для упруго деформированного стержня описывается как отношение внутренней силы N к площади сечения A. Считается положительным при растяжении, при сжатии рассматривается как отрицательное.
Абсолютная деформация зависит от жесткости сечения, величины продольной силы и длины бруса. Зависимость можно описать по следующей формуле:
Δl=Nl/EA
Таким образом, методика расчета величины абсолютного изменения длины такова: необходимо просчитать отношение значения продольной силы N умноженной на длину стержня l и жесткости сечения (произведение модуля Юнга E на площадь сечения A).
В реальных расчетах на брус действует достаточно много разнонаправленных сил, для решения таких задач требуется построение эпюр, которые могут наглядно показать какие напряжения действуют на разных участках, чем обусловлена деформация при растяжении и сжатии.
В рамках такой квазистатической (условно статической) системы, как брус или стержень с переменным сечением или отверстием, потенциальная энергия растяжения может быть рассмотрена как сумма энергий однородных участков. При проведении расчетов важно правильно разделить стержень на участки и смоделировать все участвующие в процессе силы и напряжения. Для реальных расчетов построение эпюр – сложная задача, которая требует от инженера хорошего понимания действующих на деталь нагрузок. Например, вал со шкивами разного диаметра требует сначала определения критических точек и разбивки на соответствующие участки, затем построения графиков по ним.
Деформации при растяжении сжатии
При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.
Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.
Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.
Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:
F=kx
В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.
Расчеты на прочность и жесткость
Прочность характеризует способность конструкционного материала сопротивляться внешним воздействиям без разрушений и остаточных изменений. Жесткость находится в линейной зависимости от модуля Юнга и размера сечения. Чем больше площадь, модуль упругости не меняется, тем больше жесткость. В общем случае жесткость подразумевает способность деформироваться без значительных изменений. Коэффициент запаса прочности – безразмерная величина, равная отношению предельного напряжения к допустимому. Запас прочности характеризует штатный режим работы конструкции даже с учетом случайных и не предусмотренных нагрузок. Наименьшим запасом прочности обладают пластические (1.2-2.5) и хрупкие (2-5) материалы.
Применение в расчетах этих коэффициентов позволяет, например, рассчитать опасную толщину для стержня, при которой может возникнуть максимальное нормальное напряжение. Используя коэффициент прочности и возможное предельное напряжение возможно произвести расчет необходимого диаметра вала, который гарантированно обеспечит упругую деформацию и не приведет к пластической. Для инженеров-экономистов важны расчеты наименьших безопасных размеров деталей конструкции по заданным нагрузкам.
Большинство практических расчетов на прочность и жесткость производятся для получения минимальных значений геометрических размеров конструкционных элементов и деталей машин в условиях известных внешних воздействий и необходимого и достаточного запаса прочности. Может решаться обратная задача получения значений предельных нагрузок при условии сохранения геометрических размеров и для конкретного материала.
Сложные конструкции могут быть разделены на элементарные части, для которых будут производиться расчеты, затем полученные результаты интерпретируются в рамках всей системы, для этого удобно строить эпюры распределения внешних воздействий и внутренних напряжений статически определенной системы.
С помощью известной жесткости материала делают расчеты максимально возможной длины балки или стержня (вала) при условии неизменности его сечения. Для ступенчатых валов необходимо строить эпюры воздействия внешних сил и возникающих в точках их приложения внутренних напряжений в критических точках. От правильно построенной теоретической модели будет зависеть насколько эффективно и долго прослужит вал для станка, не разрушится ли он от динамических крутящих моментов. На этапе проектирования можно выявить потенциальные слабые точки и рассчитать необходимые параметры для заданного предела прочности.
С расчетами на прочность связаны такие понятия, как срез и смятие. Срез проявляется в виде разрушения детали соединения в условиях возникновения в ее поперечном сечении перпендикулярной к нему и достаточной силы.
При расчетах соединений используют пределы текучести используемых материалов и коэффициенты запаса прочности, вычисляют максимально возможные напряжения.
Исследования на прочность обычно подразумевают решение нескольких задач: в условиях проведения поверочного расчета на проверку прочности при известных усилиях и площади сечения оценивают фактический коэффициент запаса прочности; подбор оптимального диаметра при заданных нагрузках и допустимом напряжении; вычисляют грузоподъемность или несущую способность с помощью определения внутреннего усилия при известной площади сечения и напряжении.
Прочностные расчеты при разных видах воздействий в рамках условно статических систем сложны, требуют учета многих, иногда не очевидных, факторов, их практическая ценность заключается в вычислении допустимых размеров конструкционных материалов для заданных параметров запаса прочности.
Источник
Частицы, из которых состоят твердые тела (как аморфные, так и кристаллические) постоянно совершают тепловые колебания около положений равновесия. В таких положениях энергия их взаимодействия минимальная. Если расстояние между частицами уменьшается, начинают действовать силы отталкивания, а если увеличиваться – то силы притяжения. Именно этими двумя силами обусловлены все механические свойства, которыми обладают твердые тела.
Определение 1
Если твердое тело изменяется под воздействием внешних сил, то частицы, из которых оно состоит, меняют свое внутреннее положение. Такое изменение называется деформацией.
Виды деформации
Различают деформации нескольких видов. На изображении показаны некоторые из них.
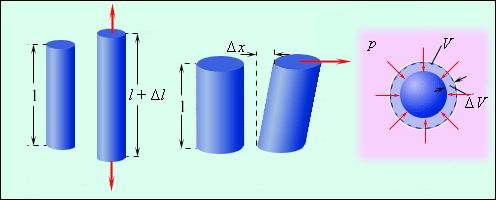
Рисунок 3.7.1. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия.
Первый вид – растяжение или сжатие – является наиболее простым видом деформации. В таком случае изменения, происходящие с телом, можно описать при помощи абсолютного удлинения Δl, которое происходит под действием сил, обозначаемых F→. Взаимосвязь, существующая между силами и удлинением, обусловлена геометрическими размерами тела (в первую очередь толщиной и длиной), а также механическими свойствами вещества.
Определение 2
Если мы разделим величину абсолютного удлинения на первоначальную длину твердого тела, мы получим величину его относительного удлинения (относительной деформации).
Обозначим этот показатель ε и запишем следующую формулу:
ε=∆ll.
Определение 3
Относительная деформация тела растет при его растяжении и соответственно уменьшается при сжатии.
Если учесть, в каком именно направлении внешняя сила действует на тело, то мы можем записать, что F будет больше нуля при растяжении и меньше нуля при сжатии.
Механическое напряжение
Определение 4
Механическое напряжение твердого тела σ – это показатель, равный отношению модуля внешней силы к площади сечения твердого тела.
σ=FS.
Величину механического напряжения принято выражать в паскалях (Па) и измерять в единицах давления.
Важно понимать, как именно механическое напряжение и относительная деформация связаны между собой. Если отобразить их взаимоотношения графически, мы получим так называемую диаграмму растяжения. При этом нам нужно отмерить величину относительной деформации по оси x, а механическое напряжение – по оси y. На рисунке ниже представлена диаграмма растяжения, типичная для меди, мягкого железа и некоторых других металлов.

Рисунок 3.7.2. Типичная диаграмма растяжения для пластичного материала. Голубая полоса – область упругих деформаций.
В тех случаях, когда деформация твердого тела меньше 1% (малая деформация), то связь между относительным удлинением и механическим напряжением приобретает линейный характер. На графике это показано на участке Oa. Если напряжение снять, то деформация исчезнет.
Определение 5
Деформация, исчезающая при снятии напряжения, называется упругой.
Линейный характер связи сохраняется до определенного предела. На графике он обозначен точкой a.
Определение 6
Предел пропорциональности – это наибольшее значение σ=σпр, при котором сохраняется линейная связь между показателями σ и ε.
На данном участке будет выполняться закон Гука:
ε=1Eσ.
В формуле содержится так называемый модуль Юнга, обозначенный буквой E.
Если мы продолжим увеличивать напряжение на твердое тело, то линейный характер связи нарушится. Это видно на участке ab. Сняв напряжение, мы также увидим практически полное исчезновение деформации, то есть восстановление формы и размеров тела.
Предел упругости
Определение 7
Предел упругости – максимальное напряжение, после снятия которого тело восстановит свою форму и размер.
После перехода этого предела восстановления первоначальных параметров тела уже не происходит. Когда мы снимаем напряжение, у тела остается так называемая остаточная (пластическая) деформация.
Определение 8
Обратите внимание на участок диаграммы bc, где напряжение практически не увеличивается, но деформация при этом продолжается. Это свойство называется текучестью материала.
Предел прочности
Определение 9
Предел прочности – максимальное напряжение, которое способно выдержать твердое тело, не разрушаясь.
В точке e материал разрушается.
Определение 10
Если диаграмма напряжения материала имеет вид, соответствующий тому, что показан на графике, то такой материал называется пластичным. У них обычно деформация, при которой происходит разрушение, заметно больше области упругих деформаций. К пластичным материалам относится большинство металлов.
Определение 11
Если материал разрушается при деформации, которая превосходит область упругих деформаций незначительно, то он называется хрупким. Такими материалами считаются чугун, фарфор, стекло и др.
Деформация сдвига имеет аналогичные закономерности и свойства. Ее отличительная особенность состоит в направлении вектора силы: он направлен по касательной относительно поверхности тела. Для поиска величины относительной деформации нам нужно найти значение Δxl, а напряжения – FS (здесь буквой S обозначена та сила, которая действует на единицу площади тела). Для малых деформаций действует следующая формула:
∆xl=1GFS
Буквой G в формуле обозначен коэффициент пропорциональности, также называемый модулем сдвига. Обычно для твердого материала он примерно в 2-3 раза меньше, чем модуль Юнга. Так, для меди E=1,1·1011 Н/м2, G=0,42·1011 Н/м2.
Когда мы имеем дело с жидкими и газообразными веществами, то важно помнить, что у них модуль сдвига равен 0.
При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях
∆VV=1Bp
Буквой B обозначен коэффициент пропорциональности, называемый модулем всестороннего сжатия. Такому сжатию можно подвергнуть не только твердое тело, но и жидкость и газ. Так, у воды B=2,2·109 Н/м2, у стали B=1,6·1011Н/м2. В Тихом океане на глубине 4 км давление составляет 4·107 Н/м2, а относительно изменения объема воды 1,8 %. Для твердого тела, изготовленного из стали, значение этого параметра равно 0,025 %, то есть оно меньше в 70 раз. Это подтверждает, что твердые тела благодаря жесткой кристаллической решетке обладают гораздо меньшей сжимаемостью по сравнению с жидкостью, в которой атомы и молекулы связаны между собой не так плотно. Газы могут сжиматься еще лучше, чем тела и жидкости.
От значения модуля всестороннего сжатия зависит скорость, с которой звук распространяется в данном веществе.
Источник
