Деформация на растяжение и сдвиг
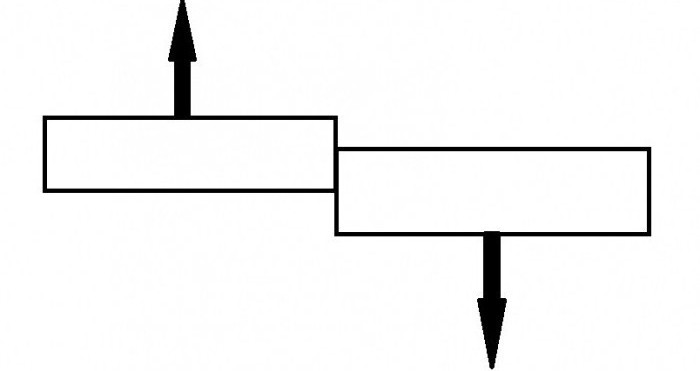
Одним из распространённых форм деформации является сдвиг отдельных слоёв изделия в вертикальной или горизонтальной плоскости. Такое смещение называется – деформация сдвига. Изменение положения может вызывать постепенное или резкое изменение первоначальной формы конструкции или отдельной детали. Виды деформации характеризуют порядок произведенного смещения и определяют порядок расчёта основных характеристик. В технической механике и сопромате рассматривают два вида деформации со сдвигом: плавное (смятие) и резкое (разрыв или срез).
Определение и общие сведения о деформации сдвига
Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным.
Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся:
- при распиловке бруса;
- отрезание или рубка металла;
- в результате нарушения целостности крепления металлических или деревянных деталей, соединённых метизами;
- балки в местах крепления опор;
- места скрепления мостовых пролётов;
- крепёж на перемычках соединения железнодорожных рельс;
- разрезания листа бумаги ножницами.
При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.
Для оценки величины сдвига и надёжности конструкции используют следующие параметры:
- величина, направление и точка приложения воздействующей силы;
- модуль сдвига;
- угол изменения внешних граней изделия;
- тангенциальное напряжение;
- модуль кручения (зависит от физико-механических характеристик материала);
Расчёт и практическое измерение этих параметров необходимы для оценки устойчивости и целостности конструкции. Формула, позволяющая вычислить допустимые изменения, учитывает все воздействия на конкретные слои детали и всю конструкции в целом.
Основными итоговыми параметрами считаются абсолютный и относительный сдвиг. Абсолютным он называется при равенстве углу возникшего отклонения от первоначального положения грани. Относительный равен частному от деления величины отклонения к расстоянию между гранями, расположенными на противоположных сторонах. Во время упругой деформации сдвига одни элементы подвергаются сжатию, другие расширению.
В случае воздействия деформации величина угла считается пропорциональной внешней силе. Увеличение степени воздействия может превратить деформацию сдвига в срез. Это приведёт к разрушению не только элементов крепления (болтов, шпилек, заклёпок), но и всей детали.
Для наглядности изменения формы детали при деформации сдвига динамика процесса обозначается с помощью величины угла смещения и векторов возникающих напряжений. Действующая сила направлена в сторону смещения слоёв рассматриваемой детали.
В современных условиях угол сдвига измеряется различными техническими приборами. Основным прибором для измерения параметров смещения является тензомер. Эти приборы работают на различных физических принципах:
- оптические (в том числе лазерные);
- акустические;
- рентгеновские; электрические;
- пневматические.
В этих приборах относительная деформация сдвига обрабатывается на современных вычислительных средствах с применением соответствующего программного обеспечения. Каждый метод обладает своими достоинствами и недостатками. Их применение зависит от поставленной задачи, технической и финансовой возможности.
Закон Гука
Основным соотношением, объединяющим физические параметры для описания протекающих процессов, является закона Гука для деформации сдвига. Этот закон позволят решить задачу нахождения угла отклонения грани объекта от исходного положения.
Небольшие напряжения вызывают углы отклонения, которые имеют небольшие величины. На итоговое значение влияют следующие параметры:
- сила упругости (её вектор направлен вдоль поверхности);
- модуль упругости второго рода;
- площадь поверхности.
Различные материалы обладают своим значением модуля упругости. Он является величиной постоянной и определяет способность материала оказывать сопротивление возникающему сдвигу.
Вычисляют касательное напряжение на гранях с помощью закона Гука. Он справедлив для малых углов и представляет произведение модуля сдвига на величину угла. Согласно теории упругости он позволяет установить связь с модулем Юнга и коэффициентом Пуассона.
Графически действие закона Гука представлено прямой линией. В качестве уравнения этой линии может использоваться уравнение прямой с угловым коэффициентом подробно описанном в аналитической геометрии. Она проходит начало координат, выбранной системы отсчёта.
Напряжение при сдвиге
Воздействие внешней силы на грань приводит к возникновению в изделии изменения формы. Все напряжения делятся на две категории: нормальные и касательные. Нормальными считаются внутренние напряжения, возникающие в различных слоях изделия, подверженного деформации.
Напряжения и деформации при сдвиге описываются с применением аналитических выражений и графических изображений. Общее состояние описывается пространственным (трёхкоординатным) напряжением. Если в конкретном случае можно выявить сечения, в которых оба вида напряжений равны нулю, можно перейти к более простым моделям описания этого процесса. Ими являются двухкоординатное (плоское) напряжённое состояние или линейное. Две последних модели являются частными случаями трёхкоординатного напряжённого состояния.
Касательные напряжения являются мерой скольжения одного поперечного слоя относительно другого. В изменениях на поверхности каждого слоя возникают только касательные напряжения. Для оценки полной картины деформации используют следующие теоретические положения:
- закон парности касательных напряжений;
- вычисление экстремальных нормальных напряжений;
- определение всех тангенциальных напряжений.
Оценка их всех при деформации смещения позволят оценить прочность конструкции.
Расчёты на прочность при сдвиге
Оценка прочностных характеристик изделий производится для определения наступления трёх моментов деформации:
- Смещение отдельных слоёв (появления угла деформации).
- Смятие элементов крепления.
- Сдвиг.
- Разрыв.
Расчёт на прочность необходим для определения условий наступления каждого из видов. На практике для более наглядной оценки характеристик прочности и стойкости к деформации решают существующие аналитические выражения и изображают эпюры отражающие направления воздействия различных видов напряжений.
Получение численных характеристик возможно благодаря применению разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений производится на основе принятых гипотез.
Расчёт допустимых напряжений производится на основании первой, третьей и четвёртой гипотезы прочности. Каждая из гипотез принимается для различных материалов, обладающих своими физико-механическими характеристиками.
Прочность находиться на каждом из этапов разработки конкретной детали. Сначала вычисляют величины допустимых напряжений и угол отклонения на предварительном (проверочном) этапе. Это позволяет определить их уровни, величины и направление приложенных сил. После этого приступают к проектированию. На этом этапе производится выбор материала детали и крепёжных элементов с учётом необходимой прочности каждого элемента конструкции. На конечном этапе ещё раз проверяют допустимые нормы нагрузки и способность готовой детали выдерживать допустимую и дополнительную нагрузку, то есть определяют запас прочности.
Наиболее показательными являются расчёты для чистого сдвига. В этом случае при расчёте рассматривают следующие аспекты решения задачи:
- Статический (составляется уравнение равновесия). В этом случае используется предположение о равномерности распределения касательных напряжений. Однако в некоторых случаях они распределяются не равномерно, что усложняет решение поставленной задачи. Он позволяет установить связь возникших напряжений с действующими внешними силами. Это производиться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
- Геометрический (деформационный). Позволяет отобразить связь между отдельными небольшими участками исследуемой детали.
- Математический. Позволяет выбрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
- Физический. Устанавливает связь между физическими процессами при деформации с учётом физических свойств материала и возникшими напряжениями (механическими свойствами).
На математическом и физическом этапе рассмотрения поставленной задачи применяются следующие основные расчетные выражения и допущения:
- закон Гука для деформации смещения;
- гипотезы прочности (с учётом физических и механических свойств выбранного материала);
- выбор системы эквивалентных напряжений;
- упрощения при изображении эпюр, отображающих направления действующих сил и возникших напряжений;
- принятие основных положений для случая чистого сдвига.
Наиболее важный практический интерес представляют два случая – смятие и разрыв.
В первом случае происходит пластическая деформация детали, когда интенсивность возникших напряжений превышает предел текучести выбранного материала. Размеры такой деформации зависят от характера и интенсивности действия внешних сил, показателей прочности материала, изменения температурного режима.
При интенсивности воздействия, превышающем прочность материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (например, метизов, заклёпок, втулок).
Разработанные методы расчёта прочности позволяют проектировать и изготавливать детали с заданием, превышающим этот предел. Это позволяет существенно повысить надёжность и долговечность всей конструкции. В настоящее время разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с применением созданных программных средств, которые позволяют получить числовые характеристики прочности и построить графические изображения эпюр в формате 3D графики.
Источник
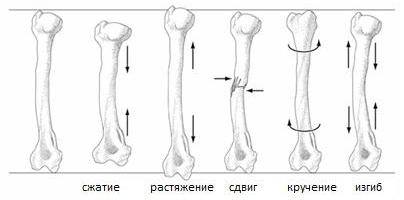
Деформация сдвига, кручения, изгиба – это изменение объема и формы тела при воздействии на него дополнительной нагрузки. При этом меняются расстояния между молекулами или атомами, приводящие к появлению сил упругости. Рассмотрим основные виды деформаций и их характеристики.

Сжатие и растяжение
Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.
Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.
Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.
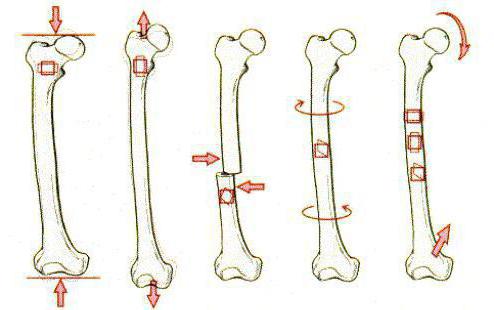
Деформация изгиба
Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.
В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.
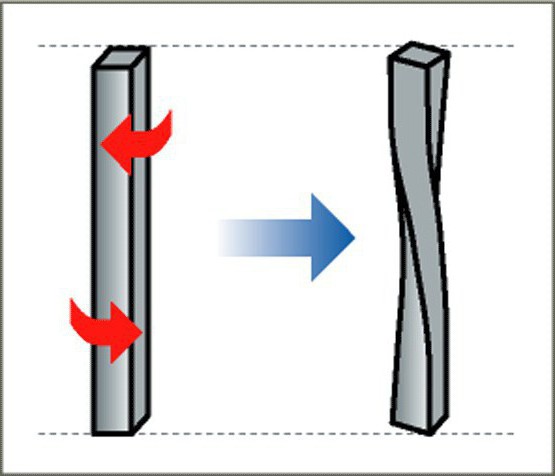
Деформация кручения
Эта продольная деформация является неоднородным сдвигом. Она возникает при действии сил, направленных параллельно либо противоположно на стержень, у которого закреплен один конец. Чаще всего сложным деформациям подвергаются различные детали и механизмы, применяемые в конструкциях и машинах. Но благодаря сочетанию нескольких вариантов деформаций, существенно облегчается вычисление их свойств.
Кстати, в процессе существенной эволюции кости птиц и животных приняли трубчатый вариант строения. Такое изменение способствовало максимальному упрочнению скелета при определенной массе тела.

Деформации на примере организма человека
Тело человека подвергается серьезным механическим нагрузкам от собственных усилий и веса, появляющихся по мере физической деятельности. Вообще, деформация (сдвиг) характерна для человеческого организма:
- Сжатие испытывает позвоночник, покровы ступней, нижние конечности.
- Растяжению подвергаются связки, верхние конечности, мышцы, сухожилья.
- Изгиб характерен для конечностей, костей таза, позвонков.
- Кручениям подвергается во время поворота шея, при вращении ее испытывают кисти рук.
Но при превышении показателей предельного напряжения, возможен разрыв, например костей плеча, бедра. В связках же ткани соединяются настолько эластично, что допускается растягивание их в два раза. Кстати, деформация сдвига объясняет всю опасность передвижения женщин на высоких каблуках. Вес тела будет переноситься на пальцы, что приведет к повышению нагрузки на кости в два раза.
По результатам медицинских осмотров, проводимых в школах, из десяти детей лишь одного можно считать здоровым. Как деформации связаны с детским здоровьем? Сдвиг, кручение, сжатие – основные причины нарушения осанки у детей и подростков.
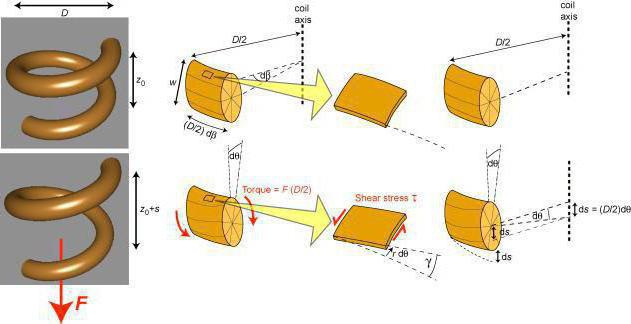
Прочность и деформации
Несмотря на многообразие живого и неживого мира, на создание человеком многочисленных материальных объектов, у всех предметов и живых существ есть общее свойство — прочность. Под ней принято понимать способность материала сохраняться на протяжении длительного временного промежутка без видимых разрушений. Существует прочность конструкций, молекул, сооружений. Эта характеристика уместна для кровеносных сосудов, человеческих костей, кирпичной колонны, стекла, воды. Деформация сдвига – вариант проверки сооружения на прочность.
Применение разных видов деформаций человеком имеет глубокие исторические корни. Все начиналось с желания соединить между собой палку и острый наконечник, чтобы охотиться на древних животных. Уже в те далекие времена человека интересовала деформация. Сдвиг, сжатие, растяжение, изгиб помогали ему создавать жилища, орудия труда, готовить пищу. По мере развития техники человечеству удалось использовать различные виды деформаций так, чтобы они приносили весомую пользу.
Закон Гука
Математические расчеты, необходимые в строительстве, технике, позволили применять закон Гука для деформации сдвига. Формула показывала прямую связь между силой, прикладываемой к телу, и его удлинением (сжатием). Гук использовал коэффициент жесткости, показывая связь между материалом и возможностью его деформации.
По мере развития и совершенствования технических средств, аппаратов и приборов, разработки теории сопротивления, были проведены серьезные исследования пластичности и упругости. Результаты проведенных фундаментальных экспериментов стали применять в строительной технике, теории сооружений, теоретической механике.
Благодаря комплексному подходу к проблемам, связанным с различными видами деформации, удалось развить строительную отрасль, осуществлять профилактику правильной осанки у подрастающего поколения страны.
Заключение
Деформации, рассматриваемые в курсе школьной физики, оказывают влияние на процессы, происходящие в живом мире. В организмах человека, животных постоянно происходит кручение, изгиб, растяжение, сжатие. И для того чтобы осуществлять своевременную и полноценную профилактику проблем, связанных с осанкой или избыточным весом, медики используют зависимости, выявленные физиками при проведении фундаментальных исследований.
Например, прежде чем осуществлять протезирование нижних конечностей, выполняется детальный расчет максимальной нагрузки, на которую он должен быть рассчитан. Протезы подбираются для каждого человека индивидуально, так как важно учесть вес, рост и подвижность последнего. При нарушениях осанки применяют специальные коррекционные пояса, основанные на использовании деформации сдвига. Современная реабилитационная медицина не смогла бы существовать без использования физических законов и явлений, в том числе и без учета закономерностей различных видов деформаций.
Источник
Деформация растяжения — вид деформации, при которой нагрузка прикладывается продольно от тела, то есть соосно или параллельно точкам крепления тела. Проще всего растяжение рассмотреть на буксировочном тросе для автомобилей. Трос имеет две точки крепления к буксиру и буксируемому объекту, по мере начала движения трос выпрямляется и начинает тянуть буксируемый объект. В натянутом состоянии трос подвергается деформации растяжения, если нагрузка меньше предельных значений, которые может он выдержать, то после снятия нагрузки трос восстановит свою форму.
Деформация растяжения является одним из основных лабораторных исследований физических свойств материалов. В ходе приложения растягивающих напряжений определяются величины, при которых материал способен:
1. воспринимать нагрузки с дальнейшим восстановлением первоначального состояния (упругая деформация)
2. воспринимать нагрузки без восстановления первоначального состояния (пластическая деформация)
3. разрушаться на пределе прочности
Данные испытания являются главными для всех тросов и веревок, которые используются для строповки, крепления грузов, альпинизма. Растяжение имеет значение также при строительстве сложных подвесных систем со свободными рабочими элементами.
Деформация сжатия
Деформация сжатия — вид деформации, аналогичный растяжению, с одним отличием в способе приложения нагрузки, ее прикладывают соосно, но по направлению к телу. Сдавливание объекта с двух сторон приводит к уменьшению его длины и одновременному упрочнению, приложение больших нагрузок образовывает в теле материала утолщения типа «бочка».
Деформация сжатия широко используется в металлургических процессах ковки металла, в ходе процесса металл получает повышенную прочность и заваривает дефекты структуры. Сжатие также важно при строительстве зданий, все элементы конструкции фундамента, свай и стен испытывают давящие нагрузки. Правильный расчет несущих конструкций здания позволяет сократить расход материалов без потери прочности.
Деформация сдвига
Деформация сдвига — вид деформации, при котором нагрузка прикладывается параллельно основанию тела. В ходе деформации сдвига одна плоскость тела смещается в пространстве относительно другой. На предельные нагрузки сдвига испытываются все крепежные элементы — болты, шурупы, гвозди. Простейший пример деформации сдвига – расшатанный стул, где за основание можно принять пол, а за плоскость приложения нагрузки – сидение.
Деформация изгиба
Деформация изгиба — вид деформации, при котором нарушается прямолинейность главной оси тела. Деформации изгиба испытывают все тела подвешенные на одной или нескольких опорах. Каждый материал способен воспринимать определенный уровень нагрузки, твердые тела в большинстве случаев способны выдерживать не только свой вес, но и заданную нагрузку. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб.
Значение деформации изгиба важно для проектирования упругих тел, таких, как мост с опорами, гимнастический брус, турник, ось автомобиля и другие.
Деформация кручения
Деформация кручения – вид деформации, при котором к телу приложен крутящий момент, вызванный парой сил, действующих в перпендикулярной плоскости оси тела. На кручение работают валы машин, шнеки буровых установок и пружины.
Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком. Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.
В словесной форме закон звучит следующим образом:
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации
Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь — сила, которой растягивают (сжимают) стержень, — абсолютное удлинение (сжатие) стержня, а — коэффициент упругости (или жёсткости).
Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения и длины ) явно, записав коэффициент упругости как
Величина называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.
Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов материала.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Модуль Юнга (модуль упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации[1]. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.
Модуль Юнга рассчитывается следующим образом:
где:
· E — модуль упругости,
· F — сила,
· S — площадь поверхности, по которой распределено действие силы,
· l — длина деформируемого стержня,
· x — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
где — плотность вещества.
Электричество
Источник
