Чистое растяжение бруса это
Под растяжением или сжатием понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают только нормальные силы (N), а все прочие внутренние силовые факторы равны нулю. Растягивающие нормальные силы (т.е. силы, направленные от поперечного сечения рис. 7.а) принято считать положительными, а сжимающие силы (т.е. силы направленные к поперечному сечению рис.7,б) — отрицательными. Этим правилом пользуемся при построении эпюр продольных сил.
Рис.7
Пример 1. Для бруса, находящегося в равновесии и нагруженного так, как показано на рис.8 а построить эпюру нормальных сил N. Разбиваем брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы.
I участок — СД, II участок — ВС, III участок — ВА.
Применяя метод сечений, оставляем правую и отбрасываем левую часть бруса: это позволяет не определять опорной реакции. Проводя произвольное сечение I-I на участке I и составляя для части бруса (рис. 8,б) уравнение равновесия Z=0, получим F-N=0, N=F
Очевидно, что все сечения на участке I равноценны. Таким образом, на участке I брус растянут силой F. Построим эпюру нормальных сил (рис.8,д). От нулевой линии, параллельной оси бруса, отложим вверх в масштабе на участке I ординаты, равные F и эпюру пометим знаком (+).
Проделаем подобные операции для участка II. Рассечём брус сечением 2-2 и рассмотрим правую отсечённую часть (рис.8,в)
Z=0 F+2F-N2=0 N2=3F
На эпюре нормальных сил на участке II отложим ординаты, равные 3F в том же масштабе, что и на участке I. Аналогично определяем нормальную силу на участке III. Проводим сечение 3-3 (рис. 8,в) и пишем уравнение равновесия Z=0
F+2F-4F+N3=0 N3=F
Рис. 8
Усилие N3 направлено к сечению, т.е. сжимает участок III. Откладываем вниз от нулевой линии ординаты, равные F и ставим знак (-) на эпюре N (рис.8,д)
Таким образом, на рис.8,д построена эпюра нормальных сил для заданного бруса; Эпюры силовых факторов штрихуются линиями, перпендикулярными оси, т.к. они являются графиками, построенными в масштабе, т.е. каждая штриховая линия представляет собой продольную силу возникающую в соответствующем поперечном сечении.
Пример 2. Брус длиною нагружен равномерно распределённой нагрузкой с интенсивностью q(кн/см) и сосредоточенной силой F приложенной на свободном торце и равной (кн) (рис.9а). Построить эпюру нормальных сил.
Для определения нормальных сил применим метод сечений. Рассечём брус на расстоянии Z от свободного торца. Отбросим верхнюю часть, а для нижней части бруса составим уравнение равновесия (рис.9,б)
Предположим, что сила N направлена вверх Z=0
N-qZ+=0 N=qZ- ()
из уравнения видно, что нормальная сила N меняется по длине бруса по линейному закону. Для построения эпюры находим значения силы в крайних сечениях: при Z=0 и при Z=
Рис. 9
Подставим эти значения Z в уравнение () и получим:
при Z=0 N=, т.е. внутренняя нормальная сила оказалась сжимающей:
при Z= N=, нормальная сила стала растягивающей. Эпюра показана на рис.9,в
Самая большая нормальная сила N= возникает на свободном торце бруса. Следовательно, это сечение самое опасное.
В местах приложения сосредоточенных сил на эпюре получаются скачки, равные величине этих сил. Следует отметить, что при определении внутренних силовых факторов можно говорить только о сечениях , удалённых от мест приложения нагрузки. Сила не может быть строго сосредоточенной в одной точке. Передача нагрузки всегда совершается по некоторой площадке, в пределах которой внутренняя сила распределяется по некоторому закону, изучение которого выходит за рамки курса «Сопротивление материалов». Таким образом, эпюра в областях приложения сосредоточенной нагрузки условна.
Источник
Рассмотрим брус
длиной ℓ постоянного поперечного
сечения А, защемленный одним концом и
нагруженный на свободном конце произвольно
направленной силой F, приложенной в
центре тяжести сечения.
Разложим
силу F на составляющие Fх,
Fу,
Fz.
В результате действия этих составляющих
получаем сочетание деформаций растяжения
и поперечного изгиба в двух взаимно
перпендикулярных плоскостях, причем
касательными напряжениями изгиба будем
в дальнейшем пренебрегать.
Применим принцип
независимости действия сил и определим
максимальные нормальные напряжения в
опасном сечении (заделке):
σt=Fz
/ A,
σ1u
= ± Fy
l /Wy
максимальные
суммарные напряжения возникнут в точке
В и будут напряжениями растяжения:
σmax
=
σB
=
FB
=
Fz
/
A + Fyℓ
/ Wx+
Fxℓ
/ Wy
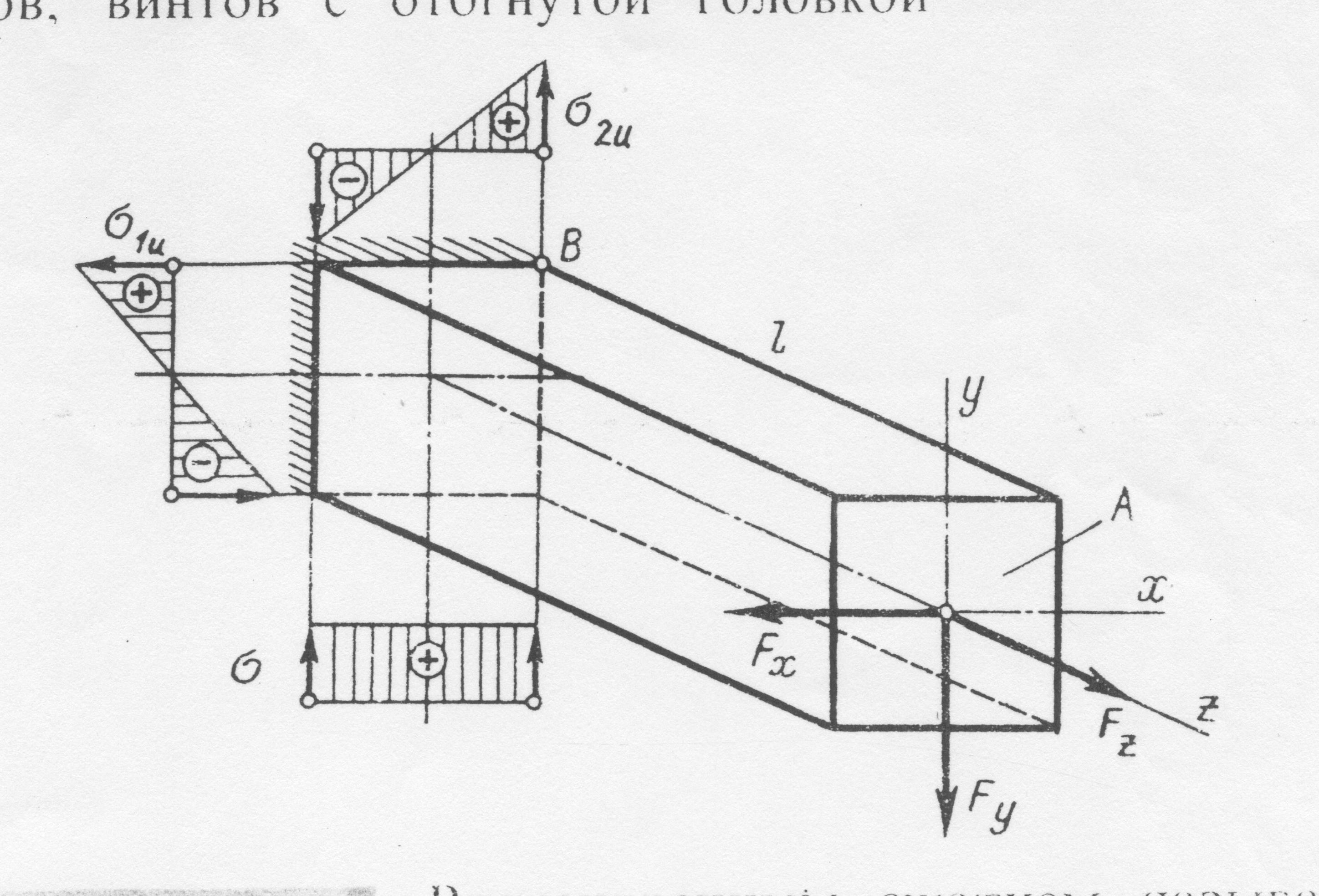
Эпюры нормальных
напряжений растяжения и изгиба
представлены на рисунке.
Деформации
растяжения и изгиба сочетаются, например,
у крюков, винтов с отогнутой головкой.
Внецентренное
сжатие.
Внецентренным сжатием называется такой
вид деформации, когда сжимающая сила
параллельна оси бруса, но точка ее
приложения не совпадает с центром
тяжести сечения (ранее изученную нами
деформацию можно назвать центральным
сжатием).
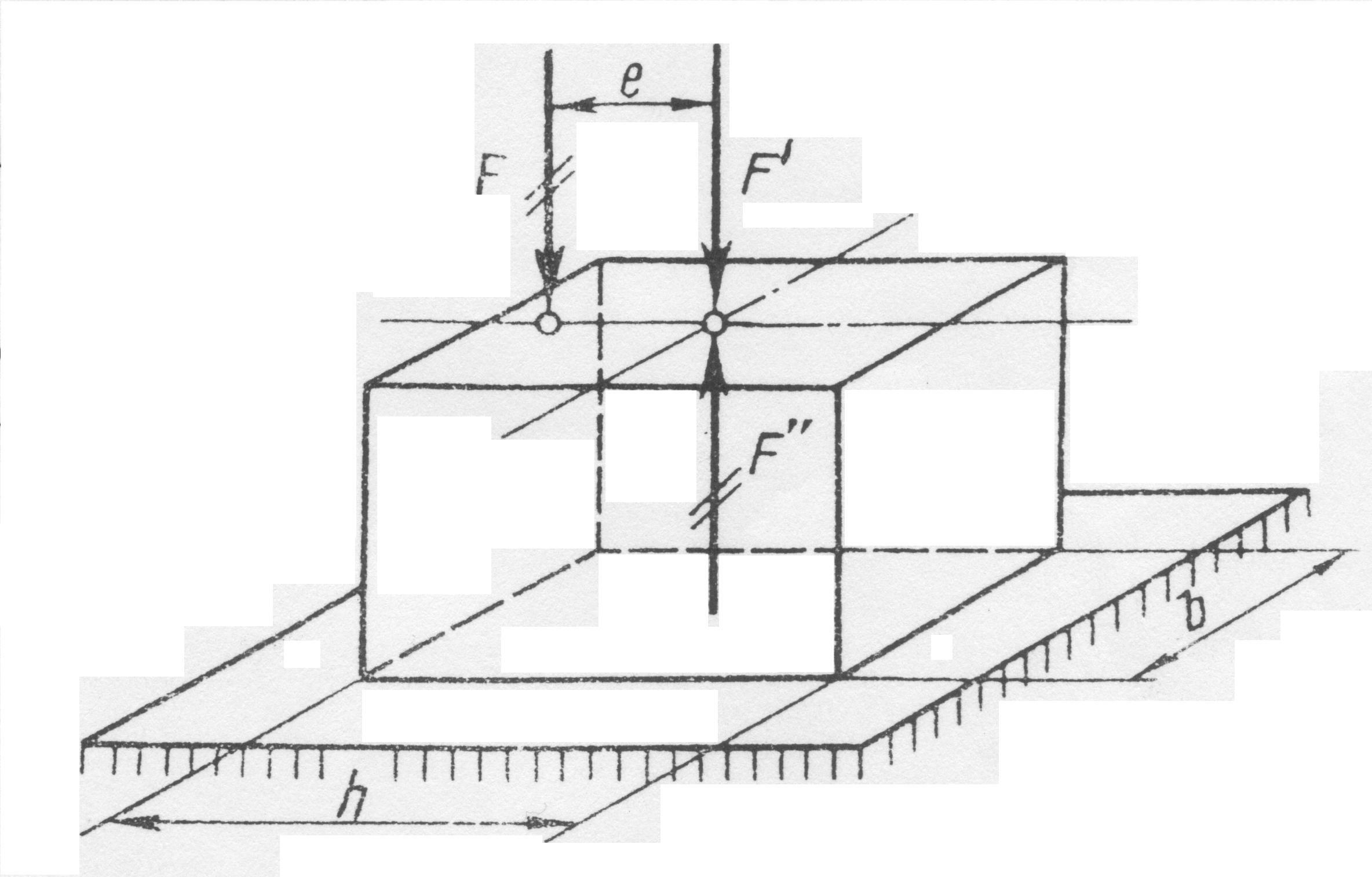
Рассмотрим
брус прямоугольного сечения А = b
· h , к которому на расстоянии ℓ от оси
приложена параллельная ей сила F.
В
центре тяжести сечения вдоль оси приложим
две противоположно направленные силы,
равные по модулю силе F. Полученную
систему трех сил будем рассматривать
как силу F, приложенную в центре тяжести,
и пару сил с моментом m=Fe.
Пользуясь принципом независимости
действия сил, внецентренное сжатие
будет рассматриваться как
сочетание центрального сжатия и чистого
изгиба,
причем соответствующие нормальные
напряжения определять по формулам
σc
= –F / A
σu =
± Mu /
W
Максимальные
суммарные напряжения будут напряжениями
сжатия:
σmax=–F/A–Fe/W
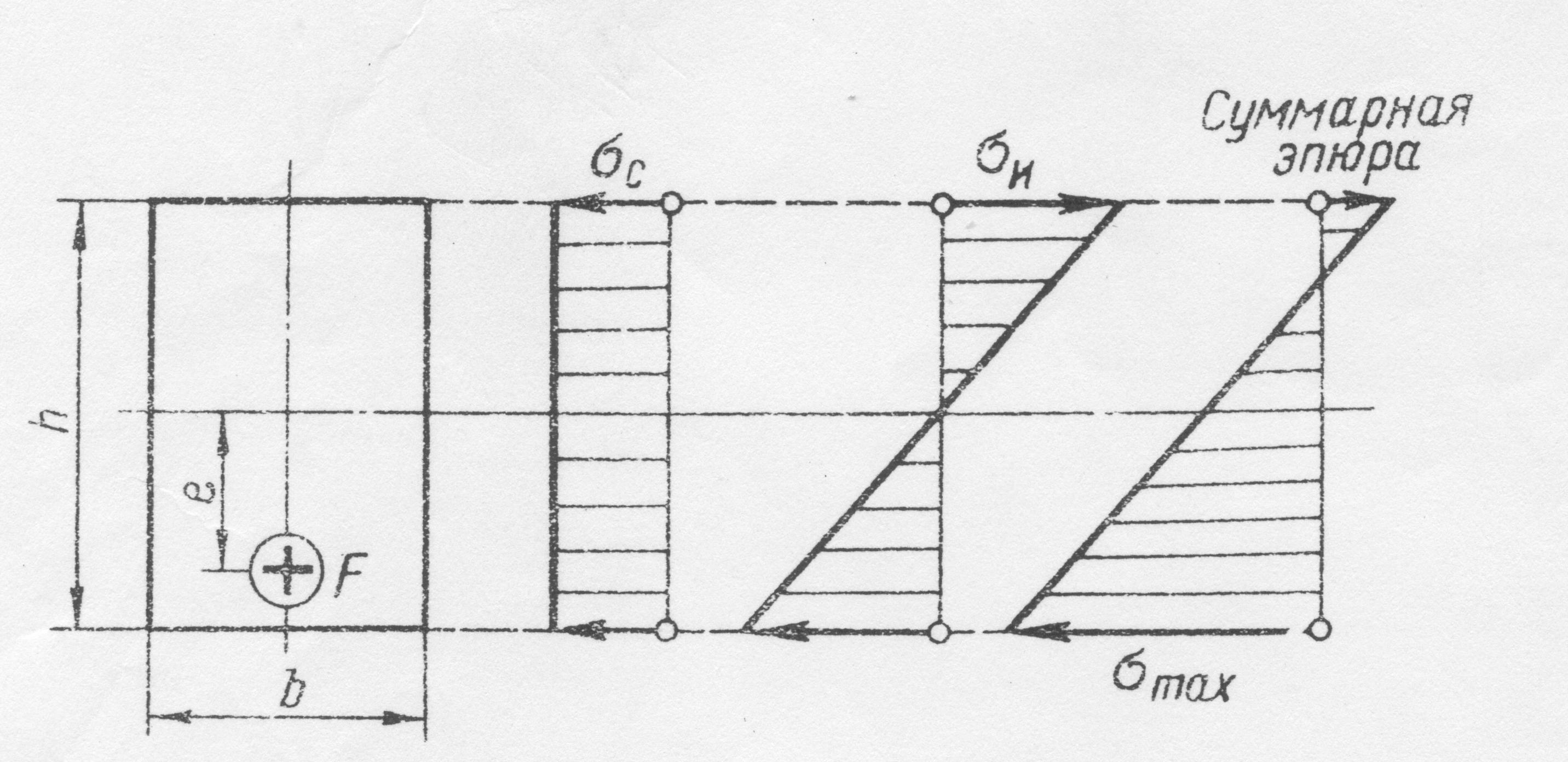
Эпюры нормальных
напряжений сжатия, изгиба и суммарная
эпюра представлены на рисунке.
2.7. Изгиб с кручением; кручение с растяжением (сжатием) Общие сведения о напряжённом состоянии в точке тела
Напряжённое
состояние в данной точке
характеризуется совокупностью нормальных
и касательных напряжений, возникающих
на бесчисленном множестве различно
ориентированных в пространстве площадок,
которые можно провести через эту точку.
Напряжённое
состояние в точке тела задано, если
известны напряжения на любых трёх
проходящих через неё взаимно
перпендикулярных площадках.
Среди бесчисленного
множества площадок, которые можно
провести через исследуемую точку,
имеются три взаимно перпендикулярные
площадки, касательные напряжения на
которых отсутствуют. Эти площадки и
возникающие на них нормальные напряжения
называют главными.
Главные напряжения
обозначают σ1,
σ2,
σ3;
при этом индексы расставляют лишь после
того, как эти напряжения вычислены, так
чтобы выполнялись алгебраические
неравенства
σ1
≥ σ2
≥ σ3
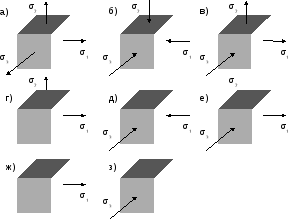
Классификация напряжённых состояний
Трёхосное,
объёмное, пространственное (все три
главных напряжения отличны от нуля)
(рис. а, б, в).Двухосное,
плоское (одно из главных напряжений
равно нулю) (рис. г, д, е).Одноосное,
линейное (только одно из главных
напряжений отлично от нуля) (рис. ж, з).
Максимальное
касательное напряжение возникает на
площадке, параллельной вектору σ2
и делящей пополам прямой угол между
площадками действия σ1
и σ3.
Это напряжение
равно полуразности максимального и
минимального главных напряжений
Площадка, на которой
возникает напряжение τmax,
отмечена на рисунке штриховкой. На
площадке, перпендикулярной отмеченной,
возникает такое же по значению касательное
напряжение.
1. Назначение
гипотез прочности
В случае одноосного
напряжённого состояния оценка прочности
в данной точке конструкции производится
путём непосредственного сопоставления
возникающего в ней рабочего напряжения
либо с предельным, либо с допускаемым
напряжением.
При
этом существует два способа оценки
прочности конструкции:
1.
2.
Предельное
напряжение определяют при механических
испытаниях данного материала на одноосное
растяжение и сжатие. Для пластичных
материалов за предельное напряжение
принимают предел текучести σУ;
для
хрупкопластичных – условный предел
текучести σ0,2;
для хрупких
– предел прочности – σU.
Возникает вопрос,
к подойти к оценке прочности в общем
случае сложного (объёмного или плоского)
напряжённого состояния.
Конечно, для любой
детали экспериментально можно найти
величины разрушающей и допускаемой
нагрузок, что освобождает нас от их
расчёта, но путь этот громоздкий и
дорогостоящий, так как разнообразие
напряжённых состояний безгранично,
велика номенклатура применяемых
материалов, и создать каждое из возможных
встречающихся в практике напряжённых
состояний, да к тому же для всех материалов,
невозможно в лабораторных условиях.
для того, чтобы
избежать сложных экспериментов и
дорогостоящих натурных испытаний (в
отдельных случаях на это идут, например,
в самолётостроении), необходимо,
располагая экспериментальными данными
определённого материала при одноосном
растяжении и сжатии, иметь возможность
оценить прочность конструкции в условиях
любого сложного напряжённого состояния.
Это становится
возможным при применении гипотез
прочности (теорий прочности, теорий
предельных напряжённых состояний.
Основная задача
гипотез прочности состоит в разработке
критерия, позволяющего сравнивать между
собой разнотипные напряжённые состояния
с точки зрения близости их к предельному
состоянию (возникновение текучести,
признаков хрупкого разрушения).
Сравнение разнотипных
напряжённых состояний производится с
помощью эквивалентного напряжённого
состояния.
Два напряжённых
состояния равноопасны
или эквивалентны,
если они переходят в предельные при
увеличении соответствующих им главных
напряжений в одно и то же число раз,
равное коэффициенту запаса прочности.
Таким образом,
коэффициенты запаса прочности для
эквивалентных напряжённых состояний
одинаковы.
Напряжение при
одноосном растяжении, равноопасное
заданному сложному напряжённому
состоянию, называют эквивалентным
напряжением (σred).
Определение
коэффициента запаса прочности по
гипотезем прочности можно представить
условной схемой:
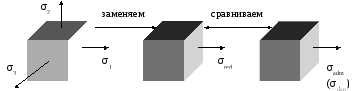
т.е сложное
напряжённое состояние заменяем
эквивалентным ему одноосным растяжением
и сравниваем соответствующее напряжение
с предельным (σdan)
или с допускаемым (σadm)
для данного материала.
Гипотезы прочности
– это гипотезы, указывающие признаки
равноопасности (критерии эквивалентности)
различных напряжённых состояний;
предположения об основной причине
достижения материалом предельного
напряжённого состояния при сочетании
основных деформаций.
2.
Гипотезы прочности
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Определение нормальной силы
Центральное растяжение (сжатие) – одно из наиболее простых видов нагружения. Методом сечений в поперечном сечении бруса обнаруживается только один внутренний силовой фактор – нормальная сила. Ее вектор перпендикулярен к поперечному сечению и направлен вдоль продольной оси бруса. Брус, работающий на растяжение-сжатие, принято называть стержнем.
Согласно методу сечений величина и направление продольной силы определяются из уравнения равновесия, составленного для отсеченной части бруса:
(2.9)
Таким образом, продольная (нормальная) сила о произвольном сечении бруса численно равна алгебраической сулеме проекций па продольную ось всех внешних (активных и реактивных) сил, приложенных к отсеченной части.
В общем случае
(2.10)
где 
– интенсивность нагрузки, распределенной вдоль оси бруса на участке от 0 до 
.
Продольная сила 
считается положительной, если она вызывает растяжение, т.е. направлена от сечения. В поперечном сечении бруса она является равнодействующей внутренних нормальных сил, возникающих в этом сечении.
График функции 
называется эпюрой нормальных сил. Из выражения (2.10) следует, что
(2.11)
т.е. интенсивность распределенной нагрузки в каждом сечении равна по величине и знаку тангенсу угла наклона касательной к эпюре 
в соответствующей рассматриваемому сечению точке эпюры.
Нормальные напряжения и деформации
При растяжении (сжатии) бруса в поперечных сечениях возникают только нормальные напряжения. Чтобы задача определения по известным N А имела единственное решение, необходимо установить закон распределения σ(x) по сечению. Для этого используется гипотеза плоских сечений (гипотеза Бернулли): сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к его оси и при деформации. Поперечные сечения лишь перемещаются вдоль оси, оставаясь параллельными друг другу.
Допустим, брус состоит из бесконечно большого числа продольных волокон. Из гипотезы Бернулли следует, что все волокна деформируются одинаково. Поскольку, согласно закону Гука, равным деформациям соответствуют равные напряжения, то при растяжении (сжатии) бруса нормальные напряжения равномерно распределяются по поперечному сечению, т.е.
;.
Как известно,
. Так как
, то 
. Отсюда
(2.12)
Положительными считаются направления 
, соответствующие растяжению.
В сечениях бруса, примыкающих к месту приложения внешних сил и к закреплениям, распределение напряжений зависит
Рис. 2.7
от способа приложения нагрузки и может быть неравномерным. Поэтому гипотеза плоских сечений в этих местах неверна.
Рассмотрим однородное напряженное состояние бруса, когда напряжения не изменяются по длине (рис. 2.7).
Изменение линейных размеров 
называется абсолютным удлинением; отношение 
– относительным удлинением или линейной деформацией.
В случае неоднородного напряженного состояния линейная деформация определяется выражением 
, где 
– приращение отрезка 
.
Между линейными деформациями 
и вызывающими их напряжениями 
существует связь, обусловленная упругими свойствами материала. Эта связь определяется законом Гука:
(2.13)
где Е – модуль упругости материала.
Рассмотрим выражение
. Согласно формуле (2.13) получим
; поскольку
Отсюда изменение длины всего бруса
(2.14)
Произведение НА называется жесткостью бруса при растяжении (сжатии).
Если законы изменения N и А различны для отдельных участков бруса, то
(2.15)
где 
– число участков.
В частном случае, когда N и А постоянны по длине бруса, получаем формулу Гука в виде
(2.16)
Итак, перемещение i-го сечения с координатой х относительно неподвижного сечения
(2.17)
Аналогично можно записать
(2.18)
где 
– перемещение начального сечения относительно заделки.
Пусть сечение бруса (см. рис. 2.7) имеет форму прямоугольника со сторонами а и b, тогда при растяжении бруса периметр его уменьшится. Величина 
характеризует относительное изменение периметра поперечного сечения и называется поперечной деформацией. Если сечение круглое, то 
. Отношение поперечной деформации к линейной величине постоянно для данного материала и называется коэффициентом Пуассона:
(2.19)
Для стали и большинства металлических материалов 
. В общем случае 
.
Источник
Содержание:
- Проверка прочности и определение необходимых размеров бруса при растяжении (сжатии)
Проверка прочности и определение необходимых размеров бруса при растяжении (сжатии)
- Испытание на прочность и определение Требуемые размеры луча Напряжение (при сжатии) В предыдущем параграфе рассматривался вопрос о распределении напряжения и деформации балки под действием продольных сил. Однако проблема того, как назначить размеры стержня для надежного и постоянного сопротивления заданной нагрузке, не была решена. Это одна из основных проблем
материального сопротивления. В условиях массового строительства возникает проблема экономии строительных материалов, чтобы полностью гарантировать долговечность конструкции. Если указаны размеры стержня, проблема определения грузоподъемности стержня, то есть стержня, может выдержать его длительную работу без каких-либо опасных изменений.
Для решения этих вопросов должны быть выполнены специальные расчеты. Есть три способа решения этих
Людмила Фирмаль
проблем. 2) Расчет допустимого напряжения, 3) Расчет предельного состояния. Все три метода имеют одинаковую цель — обеспечение прочности, долговечности и структуры. Первый метод включает определение минимальной нагрузки, которая сломает конструкцию, чтобы сравнить эту нагрузку с оценкой для строящейся конструкции. Второй метод широко использовался в строительном бизнесе до
недавнего времени и в настоящее время применяется частично, особенно в машиностроении. Согласно этому способу размеры конструктивных элементов назначаются во всех секциях таким образом, чтобы напряжение, вызванное нагрузкой, не превышало определенного допуска третьего способа, причем «младший» вступил в недавнюю жизнь Это было В настоящее время это основной метод, используемый для проектирования советских сооружений. Значение будет описано ниже. Давайте кратко рассмотрим все три метода. 721
- Способ разрушения груза «В качестве условия для прочности этого метода расчета максимальная нагрузка на конструкцию не должна превышать определенную допустимую нагрузку [P]. , (2,35) Коэффициент безопасности n принимается на основе многих соображений, таких как те, которые подробно обсуждаются в методе расчета допустимого напряжения. Рис 71А Тем не менее) Rgunit описание в списках 0L б Рис 72А Упрощенная иллюстрация растяжения (сжатия), как показано на рисунке, для определения разрушающей нагрузки в конструкции, изготовленной из материала с высокой пластичностью и относительно небольшим отверждением.
71, область текучести расширяется до бесконечности. В этом случае при центральном растяжении или сжатии сила разрыва определяется уравнением Praz = J QjdF = aTF. (2.36) F В случае хрупкого материала, необходимо взять предел прочности на разрыв Р раз = aBF вместо предела текучести. (2.37) В статически неопределенной системе пластического материала появление текучести только одного из наиболее нагруженных элементов все же не приводит к отказу системы. Например, стержень, как показано на рисунке. 72, а, появление текучести на сайте а не разрушено.
Чтобы завершить это Самоуничтожение требует текучести, которая распространяется на обе части стержня. В этом случае разрывная нагрузка (рис. 72, б),
Людмила Фирмаль
равная сумме внутренних продольных сил в двух частях стержня, определяется равенством. Рис .73d Rraz = 2gat. Кроме того, труднее определить разрушающую нагрузку, о которой идет речь, как показано на рисунке. 73, где бесконечно жесткий стержень удерживается тремя стержнями. Здесь сила Праз определяется по состоянию потока по меньшей мере двух стержней. Следовательно, если стержень AB менее нагружен, а два других стержня CD и EC являются текучими, то Prae Точно так же, предполагая, что текучесть появляется в двух стержнях AB и EC или стержнях AB и CD, можно сделать еще два уравнения. Из трех найденных значений силы в
расчет вводится наименьшая сила, которая считается разрушительной. 2. В методе допустимого напряжения максимальное напряжение в стержне не должно превышать так называемое допустимое напряжение, которое выражается как 1А. Например, условием прочности на растяжение является «,» «= -A- <I». — (2.38) г нетто Предполагая, что эффективное напряжение равно допустимому напряжению, N G1 RG —— = M- нетто Из этого уравнения можно определить требуемую площадь для данной силы или, наоборот, допустимую силу для данной площади поперечного сечения. 74допускаемые напряжения равны опасному напряжению АОП,
деленному на коэффициент безопасности р, [а] =. (2,39) • I Для хрупких материалов предел прочности при растяжении AOP = AB считается опасным напряжением. Для пластических материалов предел текучести AOP = при После появления пластической деформации становится ясно, что коэффициент запаса должен быть больше, чем P2, поскольку стержень еще не разрушен. Необходимость введения коэффициента безопасности объясняется следующими обстоятельствами: a) диапазон значений, определенный из опыта работы с этим материалом или AB. б) Рабочая нагрузка может быть
точно определена Допустимое напряжение устанавливается руководящим органом, указанным в технических характеристиках и стандартах проектирования, которые имеют силу закона и обязательны для всех инженеров и техников. В дополнение к вышеизложенным соображениям, при определении факторов безопасности и, следовательно, допустимого напряжения необходимо учитывать множество других факторов: Качество и степень однородности материала. Например, в случае стали коэффициент запаса предполагается равным примерно 1,5, в частности, -3. Для натурального камня материал очень неоднороден, а соотношение запасов составляет -10. 2. Долговечность и значимость конструкции
или машины. Например, если постоянный мост со сроком службы 50-70 лет и временный мост со сроком службы 3-5 лет изготовлены из одной и той же стали, то, конечно, в последнем случае соотношение будет равно 3. уровень. Точность расчета повышается за счет развития технологий, качества изготовления материалов и точности обработки деталей. Следовательно, с течением времени коэффициент безопасности уменьшается, а допустимое напряжение увеличивается. Например, допустимое напряжение низкоуглеродистой стали в Японии постоянно увеличивается. 753 метод предельного состояния Принимая во внимание один фактор в учете, сложно принять множество факторов, которые могут быть выявлены в разных комбинациях для разных структур. В целях более гибкого учета влияния различных факторов был предложен новый метод расчета
предельного состояния. Предельное состояние — это состояние конструкции, в которой оно останавливается для удовлетворения эксплуатационных требований. В норме различают три типа предельных состояний. В первом предельном состоянии несущая способность конструкции истощается. Все конфигурации рассчитываются в этом предельном состоянии. Второе предельное состояние — это состояние, в котором структурой трудно манипулировать из-за больших общих деформаций. В третьем критическом состоянии происходит чрезмерная локальная деформация (например, трещины образуются в железобетонных
конструкциях). Рассмотрим первый расчет предельного состояния более подробно. Испытание на прочность проводится по формуле 4 <R, (2,40) Где N — расчетная сила, создаваемая нагрузкой на элемент конструкции и определяемая по формуле N = N yit + N2P2 + N3P3 +. .., (2-41) где N! 3 — усилия от различных типов нагрузок, определенных в правиле, установленных норм (нормативная мощность); n it p2, PW — случайное отклонение от стандартных нагрузок Геометрические свойства F-сечения (под напряжением и сжимающим сечением); 7? -Расчет сопротивления материала, R = R «кило, (2.42) где R н-
нормативное сопротивление материала (в предел текучести или предел прочности при растяжении AB); 76 & <1- Случайное отклонение от стандартного сопротивления (например, сталь k = 0,94-0,85; бетон k = 0,6; древесина k = 0,34-0,9. Для пластика Где & 0D-коэффициент однородности, принятый для различных пластиков, AOD = 0,64-0,8; kac-коэффициент долговременного сопротивления, учитывающий снижение АБ вследствие длительного воздействия нагрузки. Он берется, когда & DS = 0,7 (SWAM) -? 0,3 (плексиглас, винипласт); t <D- отклонение от проектных размеров (в пределах допуска), разность проектной схемы от фактической конструкции, риск или риск AB в любой точке конструкции и (это Коэффициент составляет 0,94-1,0. Метод предельных условий подробно описан в ходе конструкций и мостов.
Смотрите также:
- Учебник по сопротивлению материалов: сопромату
Источник