Число витков пружин растяжения

Главная

Расчет
пружин

10.
Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765-86 в
ред. 1990г.

Пружина сжатия

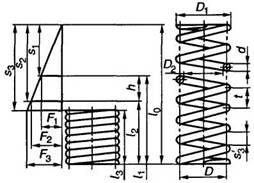
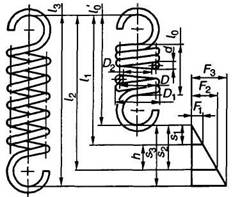
рисунок

Пружина растяжения

рисунок

Наименование параметра	Обозначение	Расчетные формулы и значения
1. Сила пружины при предварительной деформации, Н	F1	Принимаются в зависимости от нагрузки пружины
2. Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н	F2
3. Рабочий ход пружины, мм	h
4. Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с	Vmax
5. Выносливость пружины, число циклов до разрушения	NF
6. Наружный диаметр пружины, мм	D1	Предварительно назначают с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766-86-ГОСТ 13776-86
7. Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации	δ	δ = 1-F2/F3. (1) Для пружин сжатия классов I и IIδ=0,05…0,25; для пружин растяжения δ=0,05…0,10; для одножильных пружин класса IIIδ=0,10…0,40; для трехжильных класса IIIδ=0,15…0,40
8. Сила пружины при максимальной деформации, Н	F3	F3=F2/(1-δ) (2) Уточняется по таблицам ГОСТ 13766-86-ГОСТ 13776-86
9. Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н	F0	F0= (0,1… 0,25) F3
10. Диаметр проволоки, мм	d	Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86
11. Диаметр трехжильного троса, мм	d1
12. Жесткость одного витка пружины, Н/мм	c1
13. Максимальная деформация одного витка пружины, мм	s’3 (при F0=0) s»3 (при F0>0)	Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86
14. Максимальное касательное напряжение пружины, Н/мм2 (Коэффициент k см. п. 35)	τ3	Назначается по табл. 2 ГОСТ 13764-86. При проверке Для трехжильных пружин
15. Критическая скорость пружины сжатия, м/с (Максимальная скорость подвижного звена механизма vmax должна быть равна или меньше vK, т.е. vK > vmax)	vк	Для трехжильных пружин
16. Модуль сдвига, Н/мм2	G	Для пружинной стали G = 7,85·104
17. Динамическая (гравитационная) плотность материала, Н·с2/м4	Р	p = γ/g, где g-ускорение свободного падения, м/с2; γ — удельный вес, Н/м3. Для пружинной стали р = 8·103
18. Жесткость пружины, Н/мм	с	Для пружин с предварительным напряжением Для трехжильных пружин
19. Число рабочих витков пружины	n	n = c1/c (7)
20. Полное число витков пружины	n1	n1 = n+ n2, (8) где n2 — число опорных витков
21. Средний диаметр пружины, мм	D	D = D1 – d = D2 + d Для трехжильных пружин D = D1– d1= D2+ d1(9a)
22. Индекс пружины	i	i = D/d (10) Для трехжильных пружин i= D/d1 (10а) Рекомендуется назначать от 4 до 12

Наименование параметра	Обозначение	Расчетные формулы и значения
23. Коэффициент расплющивания троса в трехжильной пружине, учитывающий увеличение сечения витка вдоль оси пружины после навивки	Δ	Для трехжильного троса с углом свивки β=24° определяется по таблице, приведенной ниже
		i	40	45	50	55	60	7,0 и более
		Δ	1,029	1,021	1,015	1,010	1,005	1,000
24. Предварительная деформация пружины, мм	s1	s1=F1/c (11)
25. Рабочая деформация пружины, мм	s2	s2= F2/c (12)
26. Максимальная деформация пружины, мм	s3	s3= F3/c (13)
27. Длина пружины при максимальной деформации, мм	l3	l3 = (n1 + 1 – n3)d, (14) где n3 — число обработанных витков. Для трехжильных пружин l3 = (n + l)d1Δ. (14а) Для пружин растяжения с зацепами l3 = l0 + s3
28. Длина пружины в свободном состоянии, мм	l0	l0=l3+s3 (15)
29. Длина пружины растяжения без зацепов в свободном состоянии, мм	l0′	l0′ = (n1+1)d (15а)
30. Длина пружины при предварительной деформации, мм	1l	l1 = l0-s1. (16) Для пружин растяжения l1= l0+s1(16а)
31. Длина пружины при рабочей деформации, мм	l2	l2=l0-s2. (17) Для пружин растяжения l2=l0+s2 (17а)
32. Шаг пружины в свободном состоянии, мм	t	t = s’3+d. (18) Для трехжильных пружин t = s’3+d1Δ. (18а) Для пружин растяжения t = d(18б)
33. Напряжение в пружине при предварительной деформации, Н/мм2	τ1
34. Напряжение в пружине при рабочей деформации, Н/мм2	τ2
35. Коэффициент, учитывающий кривизну витка пружины	k	Для трехжильных пружин где
36. Длина развернутой пружины (для пружин растяжения без зацепов), мм	l
37. Масса пружины (для пружин растяжения без зацепов), кг	m
38. Объем, занимаемый пружиной (без учета зацепов пружины), мм3	V
39. Зазор между концом опорного витка и соседним рабочим витком пружины сжатия, мм	λ	Устанавливается в зависимости от формы опорного витка
40. Внутренний диаметр пружины, мм	D2	D2=D1-2d (25)
41. Временное сопротивление проволоки при растяжении, Н/мм2	Rm	Устанавливается при испытаниях проволоки или по ГОСТ 9389-75 и ГОСТ 1071-81
42. Максимальная энергия, накапливаемая пружиной, или работа деформации, МДж		Для пружин сжатия и растяжения без предварительного напряжения для пружин растяжения с предварительным напряжением

Методика
определения размеров пружин по ГОСТ 13765-86.

1. Исходными величинами для определения
размеров пружин являются силы F1 и F2, рабочий ход h,
наибольшая скорость перемещения подвижного конца пружины при нагружении или
при разгрузке vmах,
выносливость NF и наружный диаметр пружины D1 (предварительный).

Если задана только одна сила F2,
то вместо рабочего хода h для подсчета берут величину рабочей деформации s2,
соответствующую заданной силе.

2. По величине заданной выносливости NF
предварительно определяют принадлежность пружины к соответствующему классу по
табл. 1.

3. По заданной силе F2 и крайним
значениям инерционного зазора δ вычисляют по формуле (2) значение силы F3.

4. По значению F3, пользуясь табл.
2, предварительно определяют разряд пружины.

5. По табл. 11-17 находят строку, в которой наружный
диаметр витка пружины наиболее близок к предварительно заданному значению D1.
В этой же строке находят соответствующие значения силы F3 и диаметра
проволоки d.

6. Для пружин из закаливаемых марок сталей
максимальное касательное напряжение τ3 находят по табл. 2, для
пружин из холоднотянутой и термообработанной τ3
вычисляют с

учетом значений временного сопротивления Rm. Для холоднотянутой проволоки Rm определяют из ГОСТ
9389-75, для термообработанной — из ГОСТ 1071-81.

7. По полученным значениям F3 и
τ3, a также по заданному значению F2 по формулам (5)
и (5а) вычисляют критическую скорость vK и
отношение vmax/vK,
подтверждающее или

отрицающее принадлежность пружины к предварительно
установленному классу.

При несоблюдении условий vmax/vK<1 пружины I и II классов относят к
последующему классу или повторяют расчеты, изменив исходные условия. Если
невозможно изменение исходных условий, работоспособность обеспечивается
комплектом запасных пружин.

8. По окончательно установленному классу и разряду
в соответствующей таблице на параметры витков пружин, помимо ранее найденных
величин F3, D1, и d, находят величины c1 и s3,
после чего остальные размеры пружины и габариты узла вычисляют по формулам
(6)… (25).

Примеры
определения размеров пружин и формулы для проверочных расчетов жесткости и
напряжений

Пример 1. Пружина сжатия.

Дано: F1 = 20Н; F2 =
80Н; h = 30мм; D1 = 10… 12мм; vmax
= 5м/с; NF≥ 1 · 107.

По табл. 1 убеждаемся, что при заданной
выносливости NF пружину следует отнести к классу 1.

По формуле (2), пользуясь интервалом значений
δ от 0,05 до 0,25 (см. п. 7 табл. 10), находим граничные значения силы F3,
а именно:

В интервале от 84 до 107Н (ГОСТ 13766-86)
пружин класса I, разряда 1 имеются следующие силы F3: 85; 90; 95;
100 и 106Н (табл. 11).

Исходя из заданных размеров
диаметра и стремления обеспечить наибольшую критическую скорость, останавливаемся на витке со следующими
данными (номер позиции 355):

F3 = 106Н; d = 1,80мм; D1
= 12мм; с1 = 97,05Н/мм; s’3=
1,092мм.

Учитывая, что для пружин класса I норма
напряжений τ = 0,3Rm (см. табл. 2), находим, что для найденного
диаметра проволоки из углеродистой холоднотянутой стали расчетное напряжение
τ3 = 0,3·2100 = 630Н/мм2.

Принадлежность к классу I проверяем определением
отношения vmax/vK,
для чего предварительно определяем критическую скорость по формуле (5) при
δ = 0,25:

Полученная величина свидетельствует о наличии
соударения витков в данной пружине, и, следовательно, требуемая выносливость
может быть не обеспечена. Легко убедиться, что при меньших значениях силы F3
отношение vmax /vк будет еще больше отличаться от единицы
и указывать на еще большую интенсивность соударения витков.

Используем пружины класса II. Заданному
наружному диаметру и найденным выше силам F3 соответствует виток с
данными по ГОСТ 13770-86 (см. табл. 14, позиция 303): F3=95,0H;
d=1,4мм; D1=11,5мм; с1=36,58Н/мм;
s’3=2,597мм.

Учитывая норму напряжений для пружин класса
IIτ3 = 0,5Rm, находим τ3 =
0,5×2300= 1150Н/мм2.

По формуле (2) вычисляем δ = 1-F2/F3
= 1 – 80/95 = 0,16 и находим vKи
vmax /vK,
с помощью которых определяем принадлежность пружин ко II классу:

Полученная величина указывает на отсутствие
соударения витков. Следовательно, выбранная пружина удовлетворяет заданным условиям.
Пружины класса II относятся к разряду ограниченной выносливости, поэтому
следует учитывать комплектацию машины запасными пружинами с учетом опытных
данных.

Определение остальных размеров производим по
формулам табл. 10.

По формуле (6) находим жесткость пружины:

Число рабочих витков пружины определяем по
формуле (7):

n= c1/c = 36,58/2,0 = 18,29 ≈
18,5.

Уточняем жесткость пружины:

c = c1/n= 36,68/18,5 = 1,977 ≈
2,0Н/мм.

При полутора нерабочих витках полное число витков
находим по формуле (8):

n1 = n + n2 =18,5 +
1,5= 20.

По формуле (9) определяем средний диаметр
пружины:

D = 11,5 — 1,4 = 10,1мм.

Деформации, длины и шаг пружины вычисляем по
формулам (11)-(18):

На этом определение размеров пружины и
габарита узла (размер li) заканчивается.

Следует отметить, что некоторое увеличение
выносливости может быть достигнуто при использовании пружины с большей
величиной силы F3, чем найденная в
настоящем примере. С целью выяснения габаритов, занимаемых такой пружиной,
проведем анализ:

остановимся, например, на витке со следующими
данными по ГОСТ 13770-86 (см. табл. 14, позиция 313): F3 = 106Н; d =
1,4мм; D1 = 10,5мм; с1 =
50,01Н/мм; s3′ = 2,119мм.

Находим τ3 = 1150Н/мм2 и производим расчет в той же
последовательности:

Очевидно, что у этой пружины создается
большой запас на несоударяемость витков.

Далее в рассмотренном ранее порядке находим

n= 50,01/2,0 = 25,01 ≈ 25,0.

Уточненная жесткость с =50,01/25,0 ≈
2,0Н/мм;

Таким образом, устанавливаем, что применение
пружины с более высокой силой F3 хотя и привело к большему запасу на
несоударяемость витков, но оно сопровождается
увеличением габарита узла (размер l1) на 15,3мм. Можно показать,
что если выбрать виток с большим диаметром, например D1=16мм (см.
табл. 14, номер позиции 314), то тогда потребуется расширить узел по диаметру,
но при этом соответственно уменьшится размер l1.

Пример 2. Пружина сжатия.

Дано: F1 = 100Н; F2 =
250Н; h = 100мм; D1 = 15…25мм; vmax
= 10м/с.

Независимо от заданной выносливости на
основании формулы (5) можно убедиться, что при значениях 8, меньших 0,25
[формула (1)], все одножильные пружины, нагружаемые со скоростью vmax более 9,4м/с,
относятся к III классу.

По формуле (2) с учетом диапазона значений
δ для пружин класса III от 0,1 до 0,4 [формула (1)] находим границы сил F3:

Верхние значения силы F3, как
видно из табл. 2, не могут быть получены из числа одножильных конструкций,
поэтому с учетом коэффициентов δ = 0,15…0,40 [формула (1)] для
трехжильных пружин устанавливаем новые пределы F3, по формуле (2):

F3 = 294…417H.

Для указанного интервала в ГОСТ 13774-86
имеются витки со следующими силами F3: 300; 315; 335; 375 и 400Н (табл. 16а).

Исходя из заданных размеров диаметра и
наименьших габаритов узла, предварительно останавливаемся на витке со
следующими данными (номер позиции 252): F3 = 300Н; d=1,4мм; d1=3,10мм;
D1 = 17мм; с1 = 50,93Н/мм; s’3
= 5,890мм.

Согласно ГОСТ 13764-86 для пружин класса
IIIτ3 = 0,6Rm. Используя ГОСТ 9389-75, определяем
напряжение для найденного диаметра проволоки:

τ3 = 0,6 · 2300 = 1380Н/мм3.

Принадлежность к классу проверяем путем
определения величины отношения vmax/vK, для чего предварительно находим 8 и критическую
скорость по формулам (1), (2) и (5а):

Полученное неравенство свидетельствует о
наличии соударения витков и о принадлежности пружины к классу III.

Определение остальных параметров производится
по формулам табл. 10.

По формуле (6) находим жесткость:

Число рабочих витков пружины вычисляют по
формуле (7):

Уточненная жесткость:

Полное число витков находят по формуле (8):

n1 = n + 1,5 = 34,0 + 1,5 = 35,5.

По формуле (9а) определяют средний диаметр
пружины:

D = D1 – d1 = 17 — 3,10
= 13,90мм.

Деформации, длины и шаг пружины находят по
формулам табл. 10:

Проанализируем пружины, соответствующие трем
ближайшим значениям F3, взятым из ГОСТ 13774-86 (пружины класса III, разряда 1) для
рассмотренного случая (табл. 16а).

Вычисления, проделанные в аналогичном
порядке, показывают, что для трех соседних сил F3 образуется шесть
размеров пружин, удовлетворяющих требованиям по величине наружного диаметра.
Сведения о таких пружинах приведены ниже.

F3,H	300		315		335
d, мм	1,4	1,6	1,4	1,6	1,4	1,6
d1, мм	3,10	3,50	3,10	3,50	3,10	3,50
D1, мм	17,0	24,0	16,0	22,0	15,0	21,0
vmax/vK	1,43	1,50	1,16	1,21	0,942	0,984
l0, мм	317,0	273,9	355,1	309,0	405,1	337,0
l1,мм	250,4	207,2	288,4	242,3	338,4	270,3
l2, мм	150,4	107,2	188,4	142,3	238,4	170,3
n1	36,0	20,0	44,5	27,0	56,0	31,0
V,мм3	57000	93000	58000	92000	60000	93000

Из этих данных следует, что с возрастанием F3
уменьшается отношение vmax/vK и, в частности, может быть устранено
соударение витков, но вместе с этим возрастают габариты по размерам l1.

С возрастанием диаметров пружин габариты по
размерам 1Х уменьшаются, однако существенно возрастают объемы пространств, занимаемые
пружинами.

Следует отметить, что если бы для рассматриваемого
примера, в соответствии с требованиями распространенных классификаций, была
выбрана пружина класса I, то при одинаковом диаметре гнезда (D1 ≈
18мм) даже самая экономная из них потребовала бы длину гнезда l1 =
546мм, т.е. в 2,2 раза больше, чем рассмотренная выше. При этом она была бы в
11,5 раза тяжелее и, вследствие малой критической скорости (vK
= 0,7м/с), практически неработоспособной при заданной скорости нагружения 10м/с.

Пример 3. Пружина растяжения.

Дано: F1=250Н; F2=800Н;
h=100мм; D1=28…32мм; NF≥ 1 · 105.

На основании ГОСТ 13764-86 по величине NF
устанавливаем, что пружина относится к классу II (см. табл. 1.) По формуле (2)
находим силы F3, соответствующие предельной деформации:

В интервале сил 842…889Н в ГОСТ 13770-86
для пружин класса II, разряда 1 (номер пружины 494) имеется виток со следующими
параметрами: F3=850Н; D1=30мм; d = 4,5мм; с1 = 242,2Н/мм; s’3 = 3,510мм.

По заданным параметрам с помощью формулы (6)
определяем жесткость пружины:

Число рабочих витков находим по формуле (7):

Деформации и длины пружины вычисляют по
формулам [( 11Н17а)]:

Размер l2 с учетом конструкций
зацепов определяет длину гнезда для размещения пружины растяжения в узле.

Размер l3 с учетом конструкций
зацепов ограничивает деформацию пружины растяжения при заневоливании.

Трехжильные пружины (угол свивки
24°).

Жесткость

где

Напряжение

Полученные значения жесткости должны
совпадать с вычисленными по формуле (6).

Полученные значения
напряжений должны совпадать с указанными в ГОСТ 13764-86 для соответствующих
разрядов с отклонениями не более ±10%.

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Строительная механика
Теория машин и механизмов

Источник